蓝桥杯算法笔记总结
文章目录
- 1.枚举
-
- 1.1枚举简介
- 1.2例题
-
- 完美立方
- 2.二分
-
- 2.1二分简介
- 2.2二分模板
- 2.3例题
-
- 模板题——数的范围
- 蓝桥杯第8届省赛——分巧克力
- 3.贪心
-
- 3.1贪心简介
- 3.2例题
-
- 合并果子
- 4.搜索(DFS,BFS)⭐⭐⭐
-
- 4.1搜索简介
- 4.2DFS模板
- 4.3例题
-
- 全排列
- n-皇后问题
- 4.4BFS模板
- 4.5例题
- 5.动态规划(DP)⭐⭐
-
- 5.1DP问题的分析方法
-
- 5.1.1三步法:
- 5.1.2闫氏DP分析法
- 5.2背包模型及例题
-
- 01背包模型
- 5.3线性DP及例题
-
- 数字三角形
- 最长上升子序列
- 6.补充知识点
-
- 6.1前缀和⭐⭐
-
- 一维前缀和
- 二维前缀和
- 6.2最大公约数(GCD)和最小公倍数(LCM)
- 6.3双指针
-
- 最长连续不重复子序列
- 6.4并查集
-
- 并查集简介
- 并查集模板
- 例题1:合并集合
以下按照考试时想算法的思路来罗列相关知识点,按以下顺序来想算法,从枚举到DP,如果最后的DP,状态转移方程也写不出来,那就直接下一题了,下一题也做不出来,那就寄!(doge)
1.枚举
1.1枚举简介
1.2例题
完美立方
问题描述

解题思路
先将1到100中的每一个数的三次方都存入到数组中。然后枚举这其中的每一个数当作a的三次方,再枚举每一个b的三次方,c的三次方,d的三次方。如果满足条件就输出。
AC代码
#include2.二分
2.1二分简介
二分就是对当前区间序列不断取中间值,判断中间值是否合法,并更新左右指针的位置,直至重合。区间序列必须满足有序性,通常可用于求解有序区间内的最大值问题。
二分的难点:
1.check函数的编写,check是判断该值是否满足题意,满足返回true,否则返回false
2.边界的处理,一个是循环条件,一个是l和mid的关系,还有一个就是r和mid的关系,这个不能只背模板,一定要具体问题具体分析,否则会出现死循环
2.2二分模板
bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
2.3例题
模板题——数的范围
问题描述

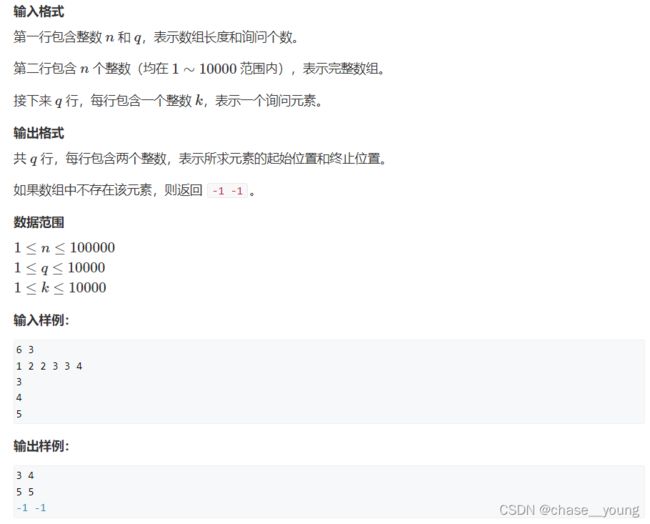
解题思路
题目给定了一个按照升序排列的数列。要求查询某个元素的起始位置和终止位置。
那很明显是要用二分去做的:l初始为0,r初始为n-1
对于查询某个元素的起始位置:
其实这个比较简单:当查询到的a[mid]小于k的时候,说明起始位置一定在mid(不包括mid)的右边,所以l=mid+1
若大于等于k,那么说明,则说明起始位置一定在mid(包括mid)的左边,所以r=mid;
对于查询某个元素的终止位置:
这个就要稍微想一想了:如果a[mid]小于等于k的话,那么终止位置一定在mid(包括mid)的右边,所以l=mid
如果a[mid]大于k的话,那么终止位置一定在mid(不包括mid)的左边,同时while终止条件要设置成l和r中间差1,这样的话,当不满足while循环的时候,l就是最大的k的位置。
然后二分就顺理成章的写下来了。
AC代码
#include蓝桥杯第8届省赛——分巧克力
题目描述


解题思路:
观察要求巧克力的最大可能边长,其实就是在边长的合法范围内求出最大值,于是就想到了利用二分来做。
首先确定好l和r的值,l的值就是1,r的值就是总面积/巧克力块数。
然后二分的难点分析:
1.check函数的编写:x是切割下来的巧克力的边长,这里首先要枚举每一块巧克力,然后就是每一块巧克力对于x边长的分割的块数=长/x*宽/x,然后累加,判断是否大于等于K,大于则返回true。
2.边界处理:对于每个确定的mid,如果check返回1,则说明满足题意,那么最大值的范围一定是[mid,r],所以l=mid+1,如果不满组题意,那么check的范围一定是[l,mid-1],所以r=mid-1。同时需要注意的是,由于C++的下取整特性,需要mid=(l+r+1)/2使其上取整。因为如果下取整,那么当l和r相差1时,若mid满足题意,那么(l+r)/2还是等于mid,此时指针不移动,陷入死循环。
至此,本道题就基本解决了。
AC代码
#include3.贪心
3.1贪心简介
贪心的意思就是不断选取当前状态下的最优解,直至满足题目条件为止。
3.2例题
合并果子
问题描述


解题思路
典型的哈夫曼树问题,不断选取当前值最小的两堆果子,将合并后的值加入到总体力耗费中去,然后再将合并后的值加入到集合中去。
AC代码
#include4.搜索(DFS,BFS)⭐⭐⭐
4.1搜索简介
一种用于遍历或搜索树或图的算法。 沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件,搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为O(!n)。
4.2DFS模板
ans;//答案,用全局变量表示
void dfs(层数,其他参数) {
if(终止条件判断) { //到达最底层,或者满足条件退出
更新答案; //更新此时的答案,答案一般用全局变量表示
return; //返回到上一层
}
(剪枝); //在进一步DFS之前进行剪枝
for(枚举下一层可能的情况) //对每一个情况继续DFS
if (used[i]==0) { //如果状态i没有用过,就可以进入下一层
used[i]=1; //标记状态,表示已经用过,在更底层时不能再使用
dfs(层数+1, 其他参数); //进入下一层
used[i]=0; //恢复状态,回溯时需要重新标记为未用过,不影响上一层对这个状态的使用
}
return; //返回到上一层
}
4.3例题
全排列
问题描述

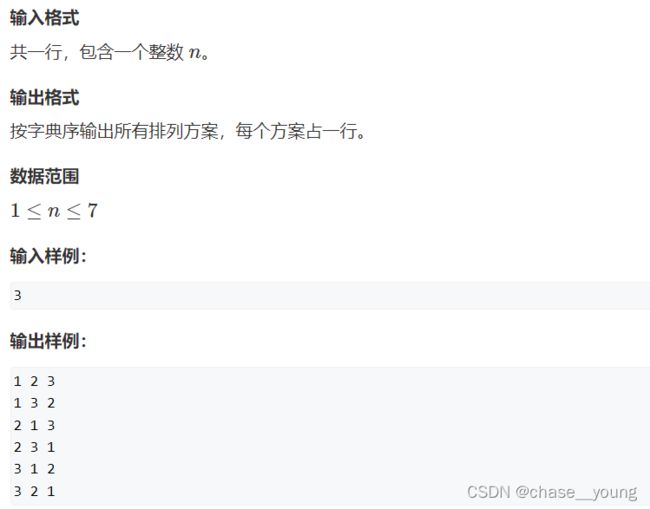
解题思路
采用DFS暴搜即可,所谓字典序,从1开始搜然后输出就是字典序。这道题完全按照上面的模板来做就行。就是要注意一个恢复现场的操作:对于p[i],若等于1,则表示第数字i在当前序列中已经用过,若等于0,则表示数字i在当前排列中还没有用过。
AC代码
#includen-皇后问题
问题描述



解题思路
同理,还是DFS问题,不过这一题需要剪枝,对于已经摆放的一个皇后,需要让他的同一行同一列两条对角线上都不能再摆放皇后。由于是按行来枚举的,所以需要让该皇后的列,两个对角线都设置限制条件。这就需要开三个数组:col[i]表示第i列方向上的元素不能再摆放皇后。
然后这里需要用到一个性质:就是棋盘上一个点的副对角线上的点的横纵坐标相加相等,所以dg[num+i]就表示同一副对角线了。同理,棋盘上任意一个点的主对角线上的点的横坐标-纵坐标也相等,但是有可能是负值,数组下标不能是负值,所以加上一个n,即udg[n+num-i]表示一条主对角线
AC代码
#include4.4BFS模板
BFS通常借助队列来实现,是对树的一种层序遍历,模板如下
定义判重数组 st[],入队时判重
定义一个队列queue
queue初始化
while(queue非空)
{
从队头取出元素t
for(拓展t)
{
ver:新节点
if(!st[ver])
{
ver进入队尾
}
}
}
4.5例题
5.动态规划(DP)⭐⭐
5.1DP问题的分析方法
5.1.1三步法:
1.定义状态:定义状态数组dp[i],通常用于问题的求解
2.寻找状态转移方程:我们要计算 dp[n] 时,是可以利用 dp[n-1],dp[n-2]……dp[1],来推出 dp[n] 的,
也就是可以利用历史数据来推出新的元素值,所以我们要找出数组元素之间的关系式,
例如 dp[n] = dp[n-1] + dp[n-2],这个就是他们的关系式了。
3.初始化:虽然我们知道了数组元素之间的关系式,例如 dp[n] = dp[n-1] + dp[n-2],
我们可以通过 dp[n-1] 和 dp[n-2] 来计算 dp[n],但是,我们得知道初始值啊,
例如一直推下去的话,会由 dp[3] = dp[2] + dp[1]。而 dp[2] 和 dp[1] 是不能再分解的了,
所以我们必须要能够直接获得 dp[2] 和 dp[1] 的值,而这,就是所谓的初始值。
5.1.2闫氏DP分析法
5.2背包模型及例题
01背包模型
AC代码
#include5.3线性DP及例题
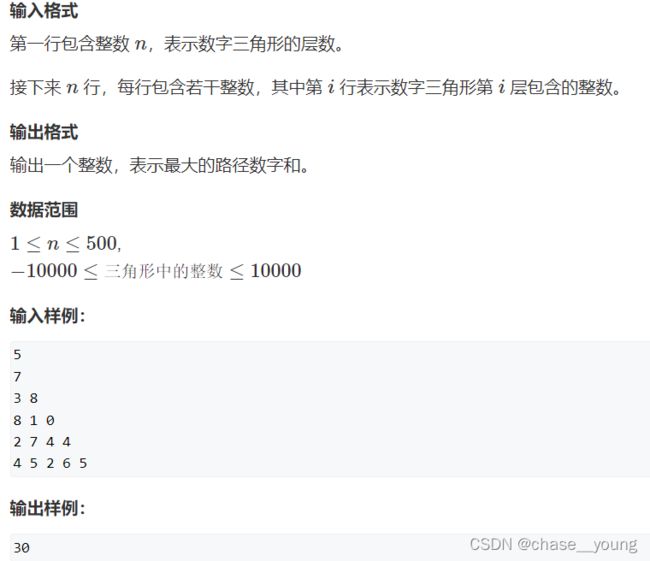
数字三角形
AC代码
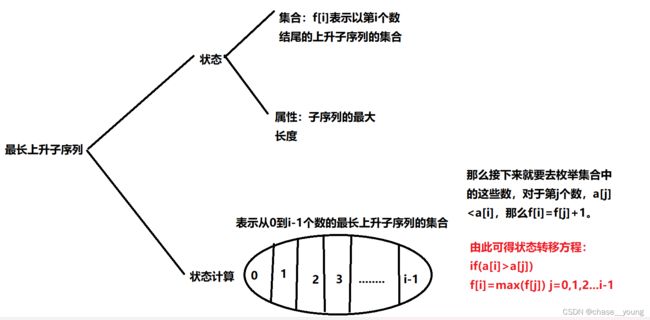
#include最长上升子序列
#include6.补充知识点
6.1前缀和⭐⭐
一维前缀和
前缀和定义:对于前1~i个数的和称为i的前缀和
S[i] = a[1] + a[2] + ... a[i]
可用于求一段区间的值:s[r]-s[l-1]表示从[l,r]的和
a[l] + ... + a[r] = S[r] - S[l - 1]
二维前缀和
S[i, j] = 第i行j列格子左上部分所有元素的和:
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]
6.2最大公约数(GCD)和最小公倍数(LCM)
GCD
#define ll long long
ll GCD(ll a, ll b)
{
return b == 0 ? a : GCD(b, a % b);
}
LCM
#define long long ll
ll LCM(ll a, ll b)
{
return a * b / GCD(a, b);
}
6.3双指针
双指针算法简介
所谓双指针,指的是在遍历对象的过程中,不是普通的使用单个指针进行访问,而是使用两个相同方向或者相反方向的指针进行扫描,从而达到相应的目的。通常能将时间复杂度从o(n^2)降低为o(n)(这里指针的意思通常是下标索引的意思)。
最长连续不重复子序列
问题描述

解题思路0
首先,题意很清楚,就是对于数组的一段区间,不能有重复的数,求这个区间的最大长度。
可以使用两重循环暴力枚举,每遇到重复数,就枚举下一个数,从下一个数开始数区间,但是这样做会超时。
本题可以考虑双指针做法,在初始状态下,i=1,j=1。先将i指针右移,并对每个数出现次数计数。每次通过while循环维护当前区间:若当前区间出现了一个数出现次数大于1,说明这个区间中出现了一个数重复出现了。则将j指针对应的数的计数-1,并且j指针不断右移,直到这个重复的数的计数=1为止。
时间复杂度o(n)
AC代码
#include 6.4并查集
并查集简介
并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题(即所谓的并、查。在进行这些操作时,时间复杂度能够近乎o(1)。
并查集模板
int find(int x) // 寻找x的祖先+路径压缩
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
关于这个find函数,首先就是这个p[x]数组,x表示待操作的数,p[x]表示了x的祖先。而find函数就是为了找到x的祖先。至于为什么这么写,我也不知道,反正就是用了个递归去找,背这么模板就好了(bushi)。
例题1:合并集合
问题描述
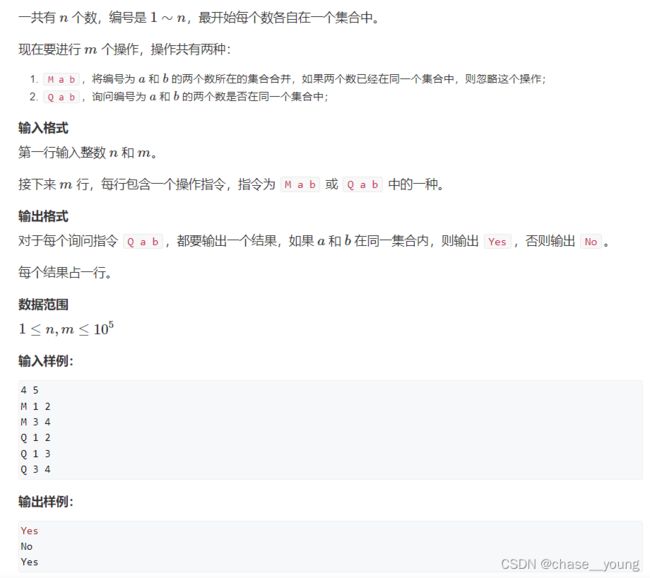
解题思路
典型的并查集,遇到合并操作时,将其中一个数比如b的祖先赋值给a即可,让a,b拥有公共祖先。
遇到查找操作,使用find函数比较这两个数的祖先是否相同即可。
AC代码
#include