朴素贝叶斯分类

朴素贝叶斯模型是一组非常简单快速的分类算法，通常适用于维度非常高的数据集。因为运行速度快，而且可调参数少，因此非常适合为分类问题提供快速粗糙的基本方案。
1、基本原理
朴素贝叶斯分类器建立在贝叶斯分类方法的基础上，其数学基础是贝叶斯定理（Bayes’s theorem）——一个描述统计量条件概率关系的公式。 在贝叶斯分类中，我们希望确定一个具有某些特征的样本属于某类标签L的概率，通常记为 P (L |特征 )。贝叶斯定理告诉我们，可以直接用下面 的公式计算这个概率
（我们举个例子吧，比如我们标签L为国籍，特征是肤色，我们的训练样本就是知道这个人是哪国人，并且特征是容易观察的，我们要求的就是当我们知道肤色特征，判断是哪国人）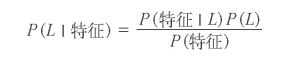
现在需要一种模型，帮我们计算每个标签的 P ( 特征| Li)。这种模型被 称为生成模型，因为它可以训练出生成输入数据的假设随机过程（或称 为概率分布）。为每种标签设置生成模型是贝叶斯分类器训练过程的主要部分。虽然这个训练步骤通常很难做，但是我们可以通过对模型进行 随机分布的假设，来简化训练工作。

之所以称为“朴素”或“朴素贝叶斯”，是因为如果对每种标签的生成模型进行非常简单的假设，就能找到每种类型生成模型的近似解，然后就可以使用贝叶斯分类。简单来说，朴素就是各个特征是相互独立的，也就是P(特征1，特征2|L)=P(特征1|L）*P(特征2|L）
不同类型的朴素贝叶斯分类器是由对数据的不同假设决定的，下面将介绍一些示例来进行演示：

2、高斯朴素贝叶斯
高斯朴素贝叶斯最容易理解的朴素贝叶斯分类器可能就是高斯朴素贝叶斯（Gaussian naive Bayes）了，这个分类器假设每个标签的数据都服从简单的高斯分布。假如你有下面的数据：

import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs 
X, y = make_blobs(100, 2, centers=2, random_state=2, cluster_std=1.5) 
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='RdBu')

通过每种类型的生成模型，可以计算出任意数据点的似然估计 （likelihood）P ( 特征| L1)，然后根据贝叶斯定理计算出后验概率比 值，从而确定每个数据点可能性最大的标签。 该步骤在 Scikit-Learn 的 sklearn.naive_bayes.GaussianNB 评估器 中实现：

from sklearn.naive_bayes import GaussianNB 
model = GaussianNB() 
model.fit(X, y)

我们再增加一些新数据预测标签，并把新数据画出来，看看决策边界：

rng = np.random.RandomState(0) 
Xnew = [-6, -14] + [14, 18] * rng.rand(2000, 2) 
ynew = model.predict(Xnew)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='RdBu') 
lim = plt.axis() 
plt.scatter(Xnew[:, 0], Xnew[:, 1], c=ynew, s=20, cmap='RdBu', alpha=0.1) 
plt.axis(lim)

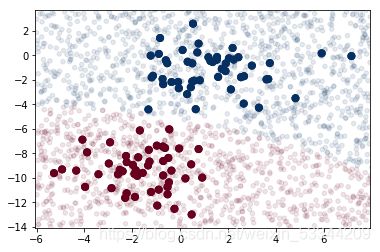
我们可以用 predict_proba 方法计算样本属于某个标签的概率

yprob = model.predict_proba(Xnew) 
print(yprob[-8:].round(2))
Out[6]: array([[ 0.89, 0.11],
 [ 1. , 0. ],
  [ 1. , 0. ], 
  [ 1. , 0. ], 
  [ 1. , 0. ], 
  [ 1. , 0. ], 
  [ 0. , 1. ], 
  [ 0.15, 0.85]])

这个数组分别给出了前两个标签的后验概率。如果你需要评估分类器的不确定性，那么这类贝叶斯方法非常有用。
当然，由于分类的最终效果只能依赖于一开始的模型假设，因此高斯朴 素贝叶斯经常得不到非常好的结果。但是，在许多场景中，尤其是特征 较多的时候，这种假设并不妨碍高斯朴素贝叶斯成为一种有用的方法。

3.多项式朴素贝叶斯
它假设特征是由一个简单多项式分布生成的。多项分布可以描述各种类型样本出现次数的概率，因此多项式朴素贝叶斯非常适合用于描述出现次数或者出现次数比例的特征。
多项式朴素贝叶斯通常用于文本分类，其特征都是指待分类文本的单词出现次数或者频次。5.4 节介绍过文本特征提取的方法，这里 用 20个网络新闻组语料库（20 Newsgroups corpus，约 20 000 篇新 闻）的单词出现次数作为特征，演示如何用多项式朴素贝叶斯对这 些新闻组进行分类：

加载数据集选取其中五类数据：

from sklearn.datasets import fetch_20newsgroups 
data = fetch_20newsgroups()
categories = ['talk.religion.misc', 'soc.religion.christian', 'sci.space', 'comp.graphics'] 
train = fetch_20newsgroups(subset='train', categories=categories) 
test = fetch_20newsgroups(subset='test', categories=categories)

为了让这些数据能用于机器学习，需要将每个字符串的内容转换成 数值向量。可以创建一个管道，将 TF–IDF 向量化方法（详情请参见上篇）与多项式朴素贝叶斯分类器组合在一起，就可以得到测试数据的预测标签：

from sklearn.feature_extraction.text import TfidfVectorizer 
from sklearn.naive_bayes import MultinomialNB 
from sklearn.pipeline import make_pipeline 
model = make_pipeline(TfidfVectorizer(), MultinomialNB())
model.fit(train.data, train.target) 
labels = model.predict(test.data)

进一步评估评估器的性能。例如，用混淆矩阵统计测试数据的真实标签与预测标签的结果：

 from sklearn.metrics import confusion_matrix 
mat = confusion_matrix(test.target, labels) 
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False, xticklabels=train.target_names, yticklabels=train.target_names) 
plt.xlabel('true label') 
plt.ylabel('predicted label')

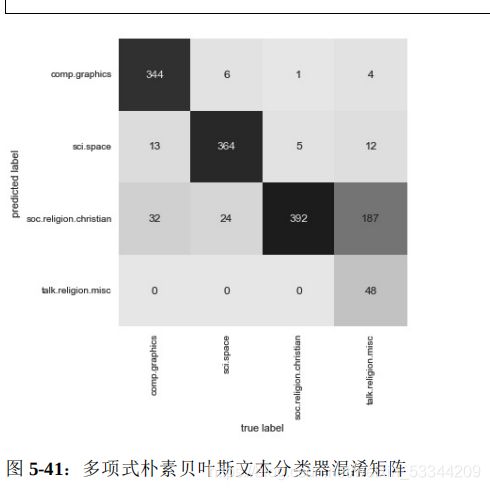
从图中可以明显看出，虽然用如此简单的分类器可以很好地区分关 于宇宙的新闻和关于计算机的新闻，但是宗教新闻和基督教新闻的 区分效果却不太好。可能是这两个领域本身就容易令人混淆！

4、朴素贝叶斯的应用场景
其优点主要体现在以下四个方面。
训练和预测的速度非常快。
直接使用概率预测。
通常很容易解释。
可调参数（如果有的话）非常少。
这些优点使得朴素贝叶斯分类器通常很适合作为分类的初始解。如果分类效果满足要求，那么万事大吉，你获得了一个非常快速且容易解释的分类器。但如果分类效果不够好，那么你可以尝试更复杂的分类模型， 与朴素贝叶斯分类器的分类效果进行对比，看看复杂模型的分类效果究竟如何。
朴素贝叶斯分类器非常适合用于以下应用场景。
假设分布函数与数据匹配（实际中很少见）。
各种类型的区分度很高，模型复杂度不重要。
非常高维度的数据，模型复杂度不重要。
后面两条看似不同，其实彼此相关：随着数据集维度的增加，任何两点都不太可能逐渐靠近,也就是容易区分，复杂度不高（毕竟它们得在每一个维度上都足够接近才行）。 也就是说，在新维度会增加样本数据信息量的假设条件下，高维数据的 簇中心点比低维数据的簇中心点更分散。因此，随着数据维度不断增加，像朴素贝叶斯这样的简单分类器的分类效果会和复杂分类器一样， 甚至更好——只要你有足够的数据，简单的模型也可以非常强大。