leetcode（622）之设计循环队列

目录

前言

1.题目描述

2. 循环链表的存储方式分析

3.实现循环队列

 3.1循环队列结构的实现

3.2 循环链表的创建

3.3 判断循环队列为空

3.4 判断队列为满

3.5 元素入循环队列操作

3.6  元素出循环队列操作

3.7 获取队首元素

3.8 获取队尾元素

3.9 循环队列的销毁

总代码

---

前言

之前给大家介绍了队列这种数据结构，但今天我给大家带来的是一种特殊的队列——循环队列，大家可以对比一下两者的不同，以及我们在实现数据结构中的灵活性。

---

1.题目描述

2. 循环链表的存储方式分析

之前我们在实现队列时我们采用的是链式结构对数据进行存储，那么在循环队列中我们应该采取哪种存储方式呢？

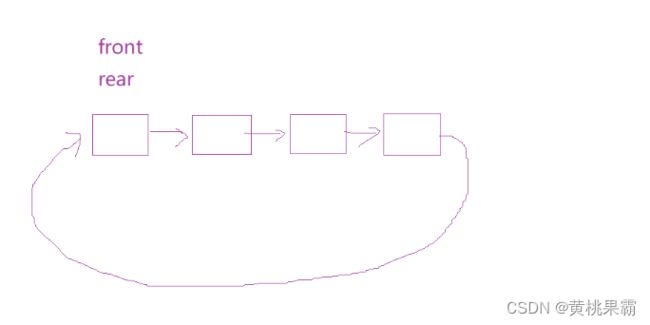
这里假设我们使用链表实现，那么我们的得到的结构是：

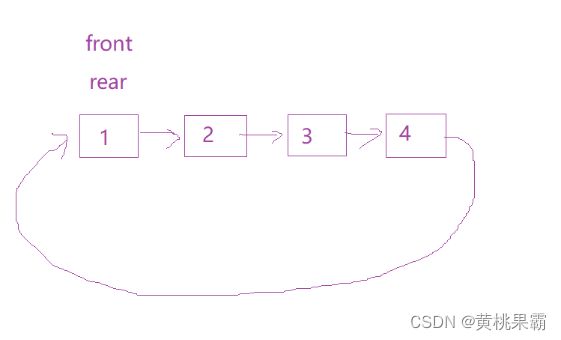
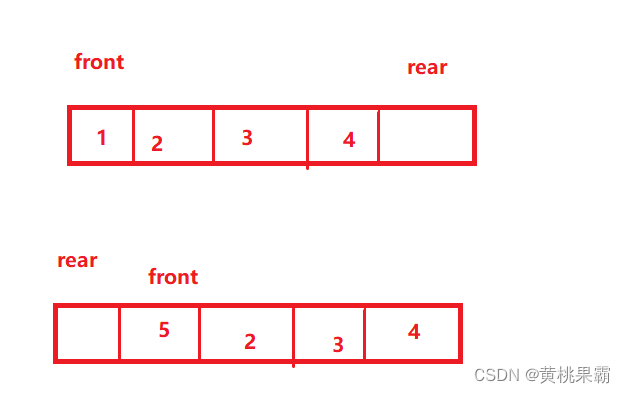
 这里的节点表示的是我们预先开辟好的空间，这里我们并没有实现对数据的存储，那么接下来我们开始进行不断对数据进行存储的操作，我们可以发现当数据满时的情况如下：（rear指针指向的是下一个数据要插入的位置）。

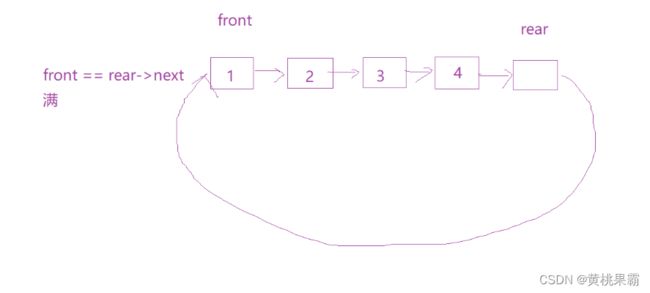
 我们这里发现当数据满后和数据为空的情况时一样的，这样我们并不好对判断空、满的函数进行合理的实现（其实我们也可以让rear指针指向的是最后一个的值，但是由于该时循环队列在插入数据时我们又要进行特殊判断，比较麻烦我们不必采用）。那么这里我们有两种方式可以合理的解决这个问题。

方式一：添加size变量来记录长度。

方式二：我们可以给循环队列多申请一个节点

第一种方式我想我不用过多给大家解释，至于第二种方式我给大家具体演示一下

 这里我们的队满条件就变为front==rear->next。

那么我们这个队列是否还可以做优化呢？这里我们可以发现，由于该为单向循环链表，方法一和方法二在进行队尾数据的情况下都有着极大的局限性，还需要我们特意去拿一个指针保存。那么这里我们可以发现顺序结构就可以合理的解决这个问题。

那么对比之前我们实现普通队列的情况我们可以发现，由于我们这里实现的是循环队列，我们并不用考虑之前出队要将后续元素全部往前移动的操作，那么这里的使用顺序表才是最优的。

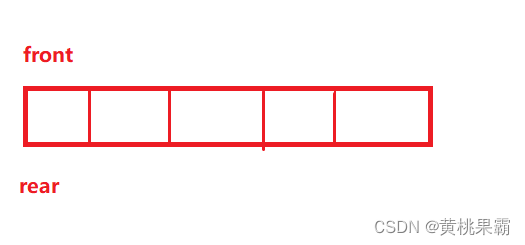
那么用顺序结构实现的情况是：

这里队列为空的情况依旧是：front==rear；

对于判断队列为满我们这里有多种情况，对于第二种情况我们的判断方式是front==rear+1,那么对于第一种情况rear+1就会出现数组越界的情况，那么我们怎么合理的解决此类问题呢，我们之前都学习了“%”这个操作符那么这里我们就可以合理的使用上，我们可以发现当我们的表达式为(rear+1)%(k+1)时是符合全部情况的，我们也可以理解为这里是一种周期循环。

3.实现循环队列

 3.1循环队列结构的实现

typedef struct {
    int *a;
    int front;
    int rear;
    int k; //循环队列存储元素的空间  
} MyCircularQueue;

3.2 循环链表的创建

MyCircularQueue* myCircularQueueCreate(int k) {
 MyCircularQueue *q=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
 if(q==NULL)
 {
     perror("malloc fail");
     return NULL;
 }
 q->a=(int*)malloc(sizeof(int)*(k+1));
 if(q->a==NULL)
 {
     perror("malloc fail");
     return NULL;
 }
 q->front=q->rear=0;
 q->k=k;
 return q;
}

由于我们需要将我们产生的循环队列传给其他函数使用，这里主函数没有创建循环队列，所以我们这里并不能使用局部变量（局部变量在函数结束的会自动销毁），这里我们用malloc函数将这个循环队列创建在栈区（栈区的变量需要我们主动销毁，或者由进程结束后自动销毁），那么我们看到函数逻辑，首先我们先传建一个队列在栈区中，然后创建一个长度为k+1的数组，然后将其他的变量赋值给初始值。最后返回我们的创建的循环队列。

3.3 判断循环队列为空

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
 assert(obj);
 return obj->front==obj->rear;
}

在之前思路分析中我们已经分析出判断为空的条件，那么我们直接使用即可。

3.4 判断队列为满

bool myCircularQueueIsFull(MyCircularQueue* obj) {
 assert(obj);
 return (obj->rear+1)%(obj->k+1)==obj->front;
}

和之前一致，我们直接使用即可。

3.5 元素入循环队列操作

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    assert(obj);
    if(myCircularQueueIsFull(obj))
    {
        return false;
    }
     obj->a[obj->rear++]=value;//这里插入我们的数据
     obj->rear %=(obj->k+1);
    return true;
}

在插入之前我们要判断循环队列是否为满的情况，这里我们直接在rear处添加我们的值，添加后我们需要把rear的值后移，但是当rear在数组最后一个时我们就会出现越界情况，所以这里我们就要进行求余操作。（当插入成功后返回真）也即：

当rear的位置小于k+1时我们进行求余操作并不影响rear的值，但是当rear越界之后我们进行求余后操作rear就会重新从数组初始位置开始往后继续往后标记位置。

3.6  元素出循环队列操作

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
  assert(obj);
  if(myCircularQueueIsEmpty(obj))
  {
      return false;
  }
    obj->front=(obj->front+1)%(obj->k+1);
    return true;
}

首先我们得判断队列是否为空，为空时即不能进行删除操作，如果可以删除我们对于循环队列出队列操作我们只需要将标记队列首元素的位置的front变量往后加一即可，演示如下

这里我们先给出一个满的循环队列 

那么接下来我们进行出队列操作。如下

 由于出队的操作我们是将front变量往后移，所以我们也得考虑到front越界的情况，所以我们也得将front进行求余操作。也即：

 当我们再继续出队操作后我们就需要将fornt进行加一求余的操作，让front标记的位置继续重最开始位置开始。

3.7 获取队首元素

int myCircularQueueFront(MyCircularQueue* obj) {
  assert(obj);
 if(myCircularQueueIsEmpty(obj))
 {
     return -1;
 }
 else
 {
     return obj->a[obj->front];
 }
}

题目要求我们不能返回时返回-1，也即是队列为空时，否则我们直接返回队首元素。

3.8 获取队尾元素

int myCircularQueueRear(MyCircularQueue* obj) {
  assert(obj);
 if(myCircularQueueIsEmpty(obj))
 {
     return -1;
 }
 else
  return obj->a[(obj->rear+obj->k)%(obj->k+1)];
}

同理在队列为为空时要求我们返回-1，我们在返回队尾元素时我们返回的是rear的前一个元素，那么我们也就可能出现越界情况，也即

 当这种情况下将rear-1就会出现数组越界情况，而实际上我们应该访问的值是数组的最后一个值那么我们这里进行的操作时将（rear-1+k+1)%(k+1)当rear-1没有越界的的位置进行求余操作后的值得到的还是rear-1的位置，当rear-1出现越界情况那么rear-1+k+1的位置到达的就是rear进行下一次循环的前一个位置，由于这个位置表示的下标是小于k+1的，那么该得到的值也就是rear上一个值。

3.9 循环队列的销毁

void myCircularQueueFree(MyCircularQueue* obj) {
  assert(obj);
  free(obj->a);
  free(obj);
}

这里我们需要注意的是我们要对之前我们在栈区开辟的空间进行销毁，这里我们需要先销毁循环队列的成员，然后再销毁这个循环队列，如果先销毁循环队列，我们就无法访问循环队列的成员变量，也就行无法销毁我们之前创建的数组。

总代码

typedef struct {
    int *a;
    int front;
    int rear;
    int k;   
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {
 MyCircularQueue *q=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
 if(q==NULL)
 {
     perror("malloc fail");
     return NULL;
 }
 q->a=(int*)malloc(sizeof(int)*(k+1));
 if(q->a==NULL)
 {
     perror("malloc fail");
     return NULL;
 }
 q->front=q->rear=0;
 q->k=k;
 return q;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
 assert(obj);
 return obj->front==obj->rear;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
 assert(obj);
 return (obj->rear+1)%(obj->k+1)==obj->front;
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    assert(obj);
    if(myCircularQueueIsFull(obj))
    {
        return false;
    }
     obj->a[obj->rear++]=value;
     obj->rear %=(obj->k+1);
    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
  assert(obj);
  if(myCircularQueueIsEmpty(obj))
  {
      return false;
  }
    obj->front=(obj->front+1)%(obj->k+1);
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) {
  assert(obj);
 if(myCircularQueueIsEmpty(obj))
 {
     return -1;
 }
 else
 {
     return obj->a[obj->front];
 }
}

int myCircularQueueRear(MyCircularQueue* obj) {
  assert(obj);
 if(myCircularQueueIsEmpty(obj))
 {
     return -1;
 }
 else
  return obj->a[(obj->rear+obj->k)%(obj->k+1)];
}

void myCircularQueueFree(MyCircularQueue* obj) {
  assert(obj);
  free(obj->a);
  free(obj);
}

运行结果：