[力扣刷题总结]（二叉树篇）

---

二叉树理论基础篇

1.二叉树的种类

在我们解题过程中二叉树有两种主要的形式：满二叉树和完全二叉树

满二叉树：

满二叉树：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。

这棵二叉树为满二叉树，也可以说深度为k，有2^k-1个节点的二叉树。

完全二叉树：

什么是完全二叉树？

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^h -1 个节点。

大家要自己看完全二叉树的定义，很多同学对完全二叉树其实不是真正的懂了。

我来举一个典型的例子如题：

优先级队列其实是一个堆，堆就是一棵完全二叉树，同时保证父子节点的顺序关系。

二叉搜索树：

前面介绍的树，都没有数值的，而二叉搜索树是有数值的了，二叉搜索树是一个有序树。

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树

下面这两棵树都是搜索树

平衡二叉搜索树：

平衡二叉搜索树：又被称为AVL（Adelson-Velsky and Landis）树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

如图：

最后一棵 不是平衡二叉树，因为它的左右两个子树的高度差的绝对值超过了1。

C++中map、set、multimap，multiset的底层实现都是平衡二叉搜索树，所以map、set的增删操作时间时间复杂度是logn，注意我这里没有说unordered_map、unordered_set，unordered_map、unordered_map底层实现是哈希表。

所以大家使用自己熟悉的编程语言写算法，一定要知道常用的容器底层都是如何实现的，最基本的就是map、set等等，否则自己写的代码，自己对其性能分析都分析不清楚！

2.二叉树的存储方式

二叉树可以链式存储，也可以顺序存储。

那么链式存储方式就用指针， 顺序存储的方式就是用数组。

顾名思义就是顺序存储的元素在内存是连续分布的，而链式存储则是通过指针把分布在散落在各个地址的节点串联一起。

链式存储如图：

链式存储是大家很熟悉的一种方式，那么我们来看看如何顺序存储呢？

其实就是用数组来存储二叉树，顺序存储的方式如图：

用数组来存储二叉树如何遍历的呢？

如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。

但是用链式表示的二叉树，更有利于我们理解，所以一般我们都是用链式存储二叉树。

所以大家要了解，用数组依然可以表示二叉树。

3.二叉树的遍历方式

关于二叉树的遍历方式，要知道二叉树遍历的基本方式都有哪些。

一些同学用做了很多二叉树的题目了，可能知道前中后序遍历，可能知道层序遍历，但是却没有框架。

我这里把二叉树的几种遍历方式列出来，大家就可以一一串起来了。

二叉树主要有两种遍历方式：

深度优先遍历：先往深走，遇到叶子节点再往回走。
广度优先遍历：一层一层的去遍历。
这两种遍历是图论中最基本的两种遍历方式，后面在介绍图论的时候 还会介绍到。

那么从深度优先遍历和广度优先遍历进一步拓展，才有如下遍历方式：

深度优先遍历

前序遍历（递归法，迭代法）
中序遍历（递归法，迭代法）
后序遍历（递归法，迭代法）

广度优先遍历

层次遍历（迭代法）

在深度优先遍历中：有三个顺序，前中后序遍历， 有同学总分不清这三个顺序，经常搞混，我这里教大家一个技巧。

这里前中后，其实指的就是中间节点的遍历顺序，只要大家记住 前中后序指的就是中间节点的位置就可以了。

看如下中间节点的顺序，就可以发现，中间节点的顺序就是所谓的遍历方式

前序遍历：中左右
中序遍历：左中右
后序遍历：左右中
大家可以对着如下图，看看自己理解的前后中序有没有问题。

最后再说一说二叉树中深度优先和广度优先遍历实现方式，我们做二叉树相关题目，经常会使用递归的方式来实现深度优先遍历，也就是实现前中后序遍历，使用递归是比较方便的。

之前我们讲栈与队列的时候，就说过栈其实就是递归的一种是实现结构，也就说前中后序遍历的逻辑其实都是可以借助栈使用非递归的方式来实现的。

而广度优先遍历的实现一般使用队列来实现，这也是队列先进先出的特点所决定的，因为需要先进先出的结构，才能一层一层的来遍历二叉树。

这里其实我们又了解了栈与队列的一个应用场景了。

具体的实现我们后面都会讲的，这里大家先要清楚这些理论基础。

4.二叉树的定义

刚刚我们说过了二叉树有两种存储方式顺序存储，和链式存储，顺序存储就是用数组来存，这个定义没啥可说的，我们来看看链式存储的二叉树节点的定义方式。

C++代码如下：

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

大家会发现二叉树的定义 和链表是差不多的，相对于链表 ，二叉树的节点里多了一个指针， 有两个指针，指向左右孩子.

这里要提醒大家要注意二叉树节点定义的书写方式。

在现场面试的时候 面试官可能要求手写代码，所以数据结构的定义以及简单逻辑的代码一定要锻炼白纸写出来。

因为我们在刷leetcode的时候，节点的定义默认都定义好了，真到面试的时候，需要自己写节点定义的时候，有时候会一脸懵逼！

|||||||||||||||||||||||二叉树的遍历方式||||||||||||||||||||||

二叉树的递归遍历

对递归不成体系，没有方法论，每次写递归算法 ，都是靠玄学来写代码，代码能不能编过都靠运气。

本篇将介绍前后中序的递归写法，一些同学可能会感觉很简单，其实不然，我们要通过简单题目把方法论确定下来，有了方法论，后面才能应付复杂的递归。

这里帮助大家确定下来递归算法的三个要素。每次写递归，都按照这三要素来写，可以保证大家写出正确的递归算法！

1.确定递归函数的参数和返回值： 确定哪些参数是递归的过程中需要处理的，那么就在递归函数里加上这个参数， 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。

2.确定终止条件： 写完了递归算法, 运行的时候，经常会遇到栈溢出的错误，就是没写终止条件或者终止条件写的不对，操作系统也是用一个栈的结构来保存每一层递归的信息，如果递归没有终止，操作系统的内存栈必然就会溢出。

3.确定单层递归的逻辑： 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。

好了，我们确认了递归的三要素，接下来就来练练手：

以下以前序遍历为例：

1.确定递归函数的参数和返回值：因为要打印出前序遍历节点的数值，所以参数里需要传入vector在放节点的数值，除了这一点就不需要在处理什么数据了也不需要有返回值，所以递归函数返回类型就是void，代码如下：

void traversal(TreeNode* cur, vector& vec)

2.确定终止条件：在递归的过程中，**如何算是递归结束了呢，当然是当前遍历的节点是空了，那么本层递归就要要结束了，所以如果当前遍历的这个节点是空，就直接return，**代码如下：

if (cur == NULL) return;

3.确定单层递归的逻辑：前序遍历是中左右的循序，所以在单层递归的逻辑，是要先取中节点的数值，代码如下：

vec.push_back(cur->val);    // 中
traversal(cur->left, vec);  // 左
traversal(cur->right, vec); // 右

单层递归的逻辑就是按照中左右的顺序来处理的，这样二叉树的前序遍历，基本就写完了，再看一下完整代码：

前序遍历：

class Solution {
public:
    void traversal(TreeNode* cur, vector& vec) {
        if (cur == NULL) return;
        vec.push_back(cur->val);    // 中
        traversal(cur->left, vec);  // 左
        traversal(cur->right, vec); // 右
    }
    vector preorderTraversal(TreeNode* root) {
        vector result;
        traversal(root, result);
        return result;
    }
};

那么前序遍历写出来之后，中序和后序遍历就不难理解了，代码如下：

中序遍历：

void traversal(TreeNode* cur, vector& vec) {
    if (cur == NULL) return;
    traversal(cur->left, vec);  // 左
    vec.push_back(cur->val);    // 中
    traversal(cur->right, vec); // 右
}

后序遍历：

void traversal(TreeNode* cur, vector& vec) {
    if (cur == NULL) return;
    traversal(cur->left, vec);  // 左
    traversal(cur->right, vec); // 右
    vec.push_back(cur->val);    // 中
}

二叉树的迭代遍历

（1）为什么可以用迭代法（非递归的方式）来实现二叉树的前后中序遍历呢？

我们在栈与队列：匹配问题都是栈的强项 (opens new window)中提到了，递归的实现就是：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。

此时大家应该知道我们用栈也可以是实现二叉树的前后中序遍历了。

（2）迭代法实现的先中后序，其实风格也不是那么统一，除了先序和后序，有关联，中序完全就是另一个风格了，一会用栈遍历，一会又用指针来遍历。

实践过的同学，也会发现使用迭代法实现先中后序遍历，很难写出统一的代码，不像是递归法，实现了其中的一种遍历方式，其他两种只要稍稍改一下节点顺序就可以了。

其实针对三种遍历方式，使用迭代法是可以写出统一风格的代码！

重头戏来了，接下来介绍一下统一写法。

我们以中序遍历为例，在二叉树：听说递归能做的，栈也能做！ (opens new window)中提到说使用栈的话，无法同时解决访问节点（遍历节点）和处理节点（将元素放进结果集）不一致的情况。

那我们就将访问的节点放入栈中，把要处理的节点也放入栈中但是要做标记。
如何标记呢，就是要处理的节点放入栈之后，紧接着放入一个空指针作为标记。 这种方法也可以叫做标记法。

1. 迭代法中序遍历

中序遍历代码如下：（详细注释）

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
                if (node->right) st.push(node->right);  // 添加右节点（空节点不入栈）

                st.push(node);                          // 添加中节点
                st.push(NULL); // 中节点访问过，但是还没有处理，加入空节点做为标记。

                if (node->left) st.push(node->left);    // 添加左节点（空节点不入栈）
            } else { // 只有遇到空节点的时候，才将下一个节点放进结果集
                st.pop();           // 将空节点弹出
                node = st.top();    // 重新取出栈中元素
                st.pop();
                result.push_back(node->val); // 加入到结果集
            }
        }
        return result;
    }
};

result数组就是最终结果集。

可以看出我们将访问的节点直接加入到栈中，但如果是处理的节点则后面放入一个空节点， 这样只有空节点弹出的时候，才将下一个节点放进结果集。

2.迭代法前序遍历

迭代法前序遍历代码如下： (注意此时我们和中序遍历相比仅仅改变了两行代码的顺序)

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop();
                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);    // 左
                st.push(node);                          // 中
                st.push(NULL);
            } else {
                st.pop();
                node = st.top();
                st.pop();
                result.push_back(node->val);
            }
        }
        return result;
    }
};

3.迭代法后序遍历

后续遍历代码如下： (注意此时我们和中序遍历相比仅仅改变了两行代码的顺序)

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop();
                st.push(node);                          // 中
                st.push(NULL);

                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);    // 左

            } else {
                st.pop();
                node = st.top();
                st.pop();
                result.push_back(node->val);
            }
        }
        return result;
    }
};

144. 二叉树的前序遍历

力扣链接
给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

示例 1：

输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入：root = []
输出：[]
示例 3：

输入：root = [1]
输出：[1]
示例 4：

输入：root = [1,2]
输出：[1,2]
示例 5：

输入：root = [1,null,2]
输出：[1,2]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

解法1：递归遍历

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void traversal(TreeNode* cur,vector<int>& result){
        if(cur == NULL) return;
        result.push_back(cur->val);//中
        traversal(cur->left, result);
        traversal(cur->right, result);
    }
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root, result);
        return result;
    }
};

复杂度分析：

时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

空间复杂度：O(n)，为递归过程中栈的开销，平均情况下为 O(logn)，最坏情况下树呈现链状，为O(n)。

解法2：迭代遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> ST;
        if(root != NULL) ST.push(root);

        while(!ST.empty()){
            TreeNode* node = ST.top();
            if(node!= NULL) {
                ST.pop();
                //you
                if(node->right) ST.push(node->right);

                //左
                if(node->left) ST.push(node->left);

                //中
                ST.push(node);
                ST.push(NULL);

            }
            else{
                ST.pop();
                node = ST.top();
                ST.pop();
                result.push_back(node->val);
            }

        }
        return result;
    }
};

复杂度分析:

时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

空间复杂度：O(n)，为迭代过程中显式栈的开销，平均情况下为 O(logn)，最坏情况下树呈现链状，为 O(n)。

二叉树的层序遍历

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。

需要借用一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑，而是用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。

而这种层序遍历方式就是图论中的广度优先遍历，只不过我们应用在二叉树上。

使用队列实现二叉树广度优先遍历，动画如下：

二叉树层序遍历的模板：

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        vector<vector<int>> result;
        while (!que.empty()) {
            int size = que.size();
            vector<int> vec;
            // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                vec.push_back(node->val);
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
            result.push_back(vec);
        }
        return result;
    }
};

116. 填充每个节点的下一个右侧节点指针

力扣链接

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

进阶：

你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

示例：

输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，‘#’ 标志着每一层的结束。

提示：

树中节点的数量少于 4096
-1000 <= node.val <= 1000

解法1：层序遍历(非常数空间)

class Solution {
public:
    Node* connect(Node* root) {
        if (root == nullptr) {
            return root;
        }
        
        // 初始化队列同时将第一层节点加入队列中，即根节点
        queue<Node*> Q;
        Q.push(root);
        
        // 外层的 while 循环迭代的是层数
        while (!Q.empty()) {
            
            // 记录当前队列大小
            int size = Q.size();
            
            // 遍历这一层的所有节点
            for(int i = 0; i < size; i++) {
                
                // 从队首取出元素
                Node* node = Q.front();
                Q.pop();
                
                // 连接
                if (i < size - 1) {
                    node->next = Q.front();
                }
                
                // 拓展下一层节点
                if (node->left != nullptr) {
                    Q.push(node->left);
                }
                if (node->right != nullptr) {
                    Q.push(node->right);
                }
            }
        }
        
        // 返回根节点
        return root;
    }
};

解法2：使用已建立的 next 指针

class Solution {
public:
    Node* connect(Node* root) {
        if (root == nullptr) {
            return root;
        }
        
        // 从根节点开始
        Node* leftmost = root;
        
        while (leftmost->left != nullptr) {
            
            // 遍历这一层节点组织成的链表，为下一层的节点更新 next 指针
            Node* head = leftmost;
            
            while (head != nullptr) {
                
                // CONNECTION 1
                head->left->next = head->right;
                
                // CONNECTION 2
                if (head->next != nullptr) {
                    head->right->next = head->next->left;
                }
                
                // 指针向后移动
                head = head->next;
            }
            
            // 去下一层的最左的节点
            leftmost = leftmost->left;
        }
        
        return root;
    }
};

103. 二叉树的锯齿形层序遍历

力扣链接
给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

树中节点数目在范围 [0, 2000] 内
-100 <= Node.val <= 100

解法1:二叉树层序遍历（空间优化）

思路：

不要插入前面或者后面，每一层的大小都知道了，直接在对应索引处赋值
代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        if(root) que.push(root);
        vector<vector<int>> result;
        bool l2r = true;
        while(!que.empty()){
            int size = que.size();
            vector<int> vec(size);
            while(size-- > 0){
                TreeNode* node = que.front();
                que.pop();
                vec[l2r?vec.size()-size-1:size] = node->val;
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            l2r = !l2r;
            result.push_back(vec);
        }
        return result;
    }
};

解法2：广度优先遍历+deque

思路：

为了满足题目要求的返回值为「先从左往右，再从右往左」交替输出的锯齿形，我们可以利用「双端队列」的数据结构来维护当前层节点值输出的顺序。

双端队列是一个可以在队列任意一端插入元素的队列。在广度优先搜索遍历当前层节点拓展下一层节点的时候我们仍然从左往右按顺序拓展，但是对当前层节点的存储我们维护一个变量 isOrderLeft 记录是从左至右还是从右至左的：

如果从左至右，我们每次将被遍历到的元素插入至双端队列的末尾。

如果从右至左，我们每次将被遍历到的元素插入至双端队列的头部。

当遍历结束的时候我们就得到了答案数组。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        vector<vector<int>> result;
        if(root) que.push(root);
        bool l2r = true;
        while(!que.empty()){
            int size = que.size();
            deque<int> level;
            while(size-- > 0){
                TreeNode* node = que.front();
                que.pop();
                if(l2r){
                    level.push_back(node->val);
                }else{
                    level.push_front(node->val);
                }
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            result.push_back(vector<int>(level.begin(),level.end()));
            l2r = !l2r;
        }
        return result;
    }
};

复杂度分析：

时间复杂度：O(N)，其中 N 为二叉树的节点数。每个节点会且仅会被遍历一次。

空间复杂度：O(N)。我们需要维护存储节点的队列和存储节点值的双端队列，空间复杂度为 O(N)。

相似题目：剑指 Offer 32 - III. 从上到下打印二叉树 III

力扣链接
请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。

例如:
给定二叉树: [3,9,20,null,null,15,7],

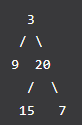
返回其层次遍历结果：

[
[3],
[20,9],
[15,7]
]

提示：

节点总数 <= 1000

解法1：层序遍历

思路：

同上
代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        queue<TreeNode*> que;

        if(root) que.push(root);
        bool l2r = false;

        while(!que.empty()){
            int size = que.size();
            vector<int> vec(size);
            for(int i = 0;i<size;i++){
                TreeNode* node = que.front();
                que.pop();

                int idx = l2r ? size-1-i : i;
                vec[idx] = node->val;
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            l2r = !l2r;
            res.push_back(vec);
        }
        return res;
    }
};

面试题 04.03. 特定深度节点链表

力扣链接
给定一棵二叉树，设计一个算法，创建含有某一深度上所有节点的链表（比如，若一棵树的深度为 D，则会创建出 D 个链表）。返回一个包含所有深度的链表的数组。

示例：

输入：[1,2,3,4,5,null,7,8]

    1
   /  \ 
  2    3
 / \    \ 
4   5    7

/
8

输出：[[1],[2,3],[4,5,7],[8]]

解法1：层序遍历+链表

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    vector<ListNode*> listOfDepth(TreeNode* tree) {
        vector<ListNode*> res;
        queue<TreeNode*> que;

        if(tree != nullptr) que.push(tree);
        
        while(!que.empty()){
            int size = que.size();
            ListNode* dummy = new ListNode(-1);
            ListNode* cur = dummy;
            for(int i = 0;i<size;i++){
                TreeNode* node = que.front();
                que.pop();
                cur->next = new ListNode(node->val);
                cur = cur->next;
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            res.push_back(dummy->next);
        }
        return res;
    }
};

958. 二叉树的完全性检验

力扣链接
给定一个二叉树的 root ，确定它是否是一个 完全二叉树 。

在一个 完全二叉树 中，除了最后一个关卡外，所有关卡都是完全被填满的，并且最后一个关卡中的所有节点都是尽可能靠左的。它可以包含 1 到 2h 节点之间的最后一级 h 。

示例 1：

输入：root = [1,2,3,4,5,6]
输出：true
解释：最后一层前的每一层都是满的（即，结点值为 {1} 和 {2,3} 的两层），且最后一层中的所有结点（{4,5,6}）都尽可能地向左。
示例 2：

输入：root = [1,2,3,4,5,null,7]
输出：false
解释：值为 7 的结点没有尽可能靠向左侧。

提示：

树的结点数在范围 [1, 100] 内。
1 <= Node.val <= 1000

解法1：层序遍历

对于一个完全二叉树，层序遍历的过程中遇到第一个空节点之后不应该再出现非空节点

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isCompleteTree(TreeNode* root) {
        //层序遍历
        queue<TreeNode*> que;
        if(root) que.push(root);
        bool reachEnd = false;
        while(!que.empty()){
            int size = que.size();
            for(int i = 0;i<size;i++){
                TreeNode* node = que.front();
                que.pop();
                //中
                if(reachEnd && node != nullptr) return false;
                if(node == nullptr){
                    reachEnd = true;
                    continue;
                }
                //左右
                que.push(node->left);
                que.push(node->right);
            }
        }
        return true;
    }
};

||||||||||||||||||||||||||二叉树的属性|||||||||||||||||||||

101. 对称二叉树

力扣链接
给定一个二叉树，检查它是否是镜像对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

1

/
2 2
/ \ /
3 4 4 3

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

1

/
2 2
\
3 3

进阶：

你可以运用递归和迭代两种方法解决这个问题吗？

解法1：递归遍历

思路：
（1）首先想清楚，判断对称二叉树要比较的是哪两个节点，要比较的可不是左右节点！

对于二叉树是否对称，要比较的是根节点的左子树与右子树是不是相互翻转的，理解这一点就知道了其实我们要比较的是两个树（这两个树是根节点的左右子树），所以在递归遍历的过程中，也是要同时遍历两棵树。

那么如果比较呢？比较的是两个子树的里侧和外侧的元素是否相等。如图所示：

那么遍历的顺序应该是什么样的呢？本题遍历只能是**“后序遍历”**，因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。

正是因为要遍历两棵树而且要比较内侧和外侧节点，所以准确的来说是一个树的遍历顺序是左右中，一个树的遍历顺序是右左中。 但都可以理解算是后序遍历，尽管已经不是严格上在一个树上进行遍历的后序遍历了。

其实后序也可以理解为是一种回溯，当然这是题外话，讲回溯的时候会重点讲的。

（2）递归三部曲

1.确定递归函数的参数和返回值
因为我们要比较的是根节点的两个子树是否是相互翻转的，进而判断这个树是不是对称树，所以要比较的是两个树，参数自然也是左子树节点和右子树节点。 返回值自然是bool类型。

代码如下：

bool compare(TreeNode* left, TreeNode* right)

2.确定终止条件
要比较两个节点数值相不相同，首先要把两个节点为空的情况弄清楚！否则后面比较数值的时候就会操作空指针了。

节点为空的情况有：（注意我们比较的其实不是左孩子和右孩子，所以如下我称之为左节点右节点）

左节点为空，右节点不为空，不对称，return false
左不为空，右为空，不对称 return false
左右都为空，对称，返回true

此时已经排除掉了节点为空的情况，那么剩下的就是左右节点不为空：

左右都不为空，比较节点数值，不相同就return false

此时左右节点不为空，且数值也不相同的情况我们也处理了。

代码如下：

if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false; // 注意这里我没有使用else

注意上面最后一种情况，我没有使用else，而是elseif， 因为我们把以上情况都排除之后，剩下的就是 左右节点都不为空，且数值相同的情况。

3.确定单层递归的逻辑
此时才进入单层递归的逻辑，单层递归的逻辑就是处理 左右节点都不为空，且数值相同的情况。

比较二叉树外侧是否对称：传入的是左节点的左孩子，右节点的右孩子。
比较内测是否对称，传入左节点的右孩子，右节点的左孩子。
如果左右都对称就返回true ，有一侧不对称就返回false 。
代码如下：

bool outside = compare(left->left, right->right);   // 左子树：左、 右子树：右
bool inside = compare(left->right, right->left);    // 左子树：右、 右子树：左
bool isSame = outside && inside;                    // 左子树：中、 右子树：中（逻辑处理）
return isSame;

代码：

class Solution {
public:
    bool compare(TreeNode* left, TreeNode* right) {
        // 首先排除空节点的情况
        if (left == NULL && right != NULL) return false;
        else if (left != NULL && right == NULL) return false;
        else if (left == NULL && right == NULL) return true;
        // 排除了空节点，再排除数值不相同的情况
        else if (left->val != right->val) return false;

        // 此时就是：左右节点都不为空，且数值相同的情况
        // 此时才做递归，做下一层的判断
        bool outside = compare(left->left, right->right);   // 左子树：左、 右子树：右
        bool inside = compare(left->right, right->left);    // 左子树：右、 右子树：左
        bool isSame = outside && inside;                    // 左子树：中、 右子树：中 （逻辑处理）
        return isSame;

    }
    bool isSymmetric(TreeNode* root) {
        if (root == NULL) return true;
        return compare(root->left, root->right);
    }
};

复杂度分析：

假设树上一共 n 个节点。

时间复杂度：这里遍历了这棵树，渐进时间复杂度为O(n)。
空间复杂度：这里的空间复杂度和递归使用的栈空间有关，这里递归层数不超过 n，故渐进空间复杂度为O(n)。

解法2：迭代遍历+队列

思路：
注意，这里的迭代法可不是前中后序的迭代写法，因为本题的本质是判断两个树是否是相互翻转的，其实已经不是所谓二叉树遍历的前中后序的关系了。

这里我们可以使用队列来比较两个树（根节点的左右子树）是否相互翻转，（注意这不是层序遍历）

通过队列来判断根节点的左子树和右子树的内侧和外侧是否相等，如动画所示：

如下的条件判断和递归的逻辑是一样的。

代码：

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (root == NULL) return true;
        queue<TreeNode*> que;
        que.push(root->left);   // 将左子树头结点加入队列
        que.push(root->right);  // 将右子树头结点加入队列
        
        while (!que.empty()) {  // 接下来就要判断这两个树是否相互翻转
            TreeNode* leftNode = que.front(); que.pop();
            TreeNode* rightNode = que.front(); que.pop();
            if (!leftNode && !rightNode) {  // 左节点为空、右节点为空，此时说明是对称的
                continue;
            }

            // 左右一个节点不为空，或者都不为空但数值不相同，返回false
            if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
                return false;
            }
            que.push(leftNode->left);   // 加入左节点左孩子
            que.push(rightNode->right); // 加入右节点右孩子
            que.push(leftNode->right);  // 加入左节点右孩子
            que.push(rightNode->left);  // 加入右节点左孩子
        }
        return true;
    }
};

复杂度分析：

时间复杂度：O(n)，同「方法一」。
空间复杂度：这里需要用一个队列来维护节点，每个节点最多进队一次，出队一次，队列中最多不会超过 n 个点，故渐进空间复杂度为 O(n)。

解法2：迭代遍历+栈

思路：

可以发现，这个迭代法，其实是把左右两个子树要比较的元素顺序放进一个容器，然后成对成对的取出来进行比较，那么其实使用栈也是可以的。只要把队列原封不动的改成栈就可以了。

代码：

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (root == NULL) return true;
        stack<TreeNode*> st; // 这里改成了栈
        st.push(root->left);
        st.push(root->right);
        while (!st.empty()) {
            TreeNode* leftNode = st.top(); st.pop();
            TreeNode* rightNode = st.top(); st.pop();
            if (!leftNode && !rightNode) {
                continue;
            }
            if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
                return false;
            }
            st.push(leftNode->left);
            st.push(rightNode->right);
            st.push(leftNode->right);
            st.push(rightNode->left);
        }
        return true;
    }
};

112. 路径总和

力扣链接
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

解法1：DFS-递归

思路：
这道题我们要遍历从根节点到叶子节点的的路径看看总和是不是目标和

可以使用深度优先遍历的方式（本题前中后序都可以，无所谓，因为中节点也没有处理逻辑）来遍历二叉树

1.确定递归函数的参数和返回类型

参数：需要二叉树的根节点，还需要一个计数器，这个计数器用来计算二叉树的一条边之和是否正好是目标和，计数器为int型。

再来看返回值，递归函数什么时候需要返回值？什么时候不需要返回值？这里总结如下三点：

…如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。（这种情况就是本文下半部分介绍的113.路径总和ii）

…如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。 （这种情况我们在236. 二叉树的最近公共祖先 (opens new window)中介绍）

…如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（本题的情况）

而本题我们要找一条符合条件的路径，所以递归函数需要返回值，及时返回，那么返回类型是什么呢？

如图所示：

图中可以看出，遍历的路线，并不要遍历整棵树，所以递归函数需要返回值，可以用bool类型表示。

所以代码如下：

bool traversal(treenode* cur, int count)   // 注意函数的返回类型

2.确定终止条件

首先计数器如何统计这一条路径的和呢？

不要去累加然后判断是否等于目标和，那么代码比较麻烦，可以用递减，让计数器count初始为目标和，然后每次减去遍历路径节点上的数值。

如果最后count == 0，同时到了叶子节点的话，说明找到了目标和。

如果遍历到了叶子节点，count不为0，就是没找到。

递归终止条件代码如下：

if (!cur->left && !cur->right && count == 0) return true; // 遇到叶子节点，并且计数为0
if (!cur->left && !cur->right) return false; // 遇到叶子节点而没有找到合适的边，直接返回

3.确定单层递归的逻辑

因为终止条件是判断叶子节点，所以递归的过程中就不要让空节点进入递归了。

递归函数是有返回值的，如果递归函数返回true，说明找到了合适的路径，应该立刻返回。

代码如下：

if (cur->left) { // 左 （空节点不遍历）
    // 遇到叶子节点返回true，则直接返回true
    if (traversal(cur->left, count - cur->left->val)) return true; // 注意这里有回溯的逻辑
}
if (cur->right) { // 右 （空节点不遍历）
    // 遇到叶子节点返回true，则直接返回true
    if (traversal(cur->right, count - cur->right->val)) return true; // 注意这里有回溯的逻辑
}
return false;

以上代码中是包含着回溯的，没有回溯，如何后撤重新找另一条路径呢。

回溯隐藏在traversal(cur->left, count - cur->left->val)这里， 因为把count - cur->left->val 直接作为参数传进去，函数结束，count的数值没有改变。

为了把回溯的过程体现出来，可以改为如下代码：

if (cur->left) { // 左
    count -= cur->left->val; // 递归，处理节点;
    if (traversal(cur->left, count)) return true;
    count += cur->left->val; // 回溯，撤销处理结果
}
if (cur->right) { // 右
    count -= cur->right->val;
    if (traversal(cur->right, count)) return true;
    count += cur->right->val;
}
return false;

整体代码如下：

class solution {
private:
    bool traversal(treenode* cur, int count) {
        if (!cur->left && !cur->right && count == 0) return true; // 遇到叶子节点，并且计数为0
        if (!cur->left && !cur->right) return false; // 遇到叶子节点直接返回

        if (cur->left) { // 左
            count -= cur->left->val; // 递归，处理节点;
            if (traversal(cur->left, count)) return true;
            count += cur->left->val; // 回溯，撤销处理结果
        }
        if (cur->right) { // 右
            count -= cur->right->val; // 递归，处理节点;
            if (traversal(cur->right, count)) return true;
            count += cur->right->val; // 回溯，撤销处理结果
        }
        return false;
    }

public:
    bool haspathsum(treenode* root, int sum) {
        if (root == null) return false;
        return traversal(root, sum - root->val);
    }
};

以上代码精简之后如下：

class solution {
public:
    bool haspathsum(treenode* root, int sum) {
        if (root == null) return false;
        if (!root->left && !root->right && sum == root->val) {
            return true;
        }
        return haspathsum(root->left, sum - root->val) || haspathsum(root->right, sum - root->val);
    }
};

解法2：DFS-迭代

如果使用栈模拟递归的话，那么如果做回溯呢？

此时栈里一个元素不仅要记录该节点指针，还要记录从头结点到该节点的路径数值总和。

c++就我们用pair结构来存放这个栈里的元素。

定义为：pair pair<节点指针，路径数值>

这个为栈里的一个元素。

如下代码是使用栈模拟的前序遍历，如下：（详细注释）

class solution {

public:
    bool haspathsum(treenode* root, int sum) {
        if (root == null) return false;
        // 此时栈里要放的是pair<节点指针，路径数值>
        stack<pair<treenode*, int>> st;
        st.push(pair<treenode*, int>(root, root->val));
        while (!st.empty()) {
            pair<treenode*, int> node = st.top();
            st.pop();
            // 如果该节点是叶子节点了，同时该节点的路径数值等于sum，那么就返回true
            if (!node.first->left && !node.first->right && sum == node.second) return true;

            // 右节点，压进去一个节点的时候，将该节点的路径数值也记录下来
            if (node.first->right) {
                st.push(pair<treenode*, int>(node.first->right, node.second + node.first->right->val));
            }

            // 左节点，压进去一个节点的时候，将该节点的路径数值也记录下来
            if (node.first->left) {
                st.push(pair<treenode*, int>(node.first->left, node.second + node.first->left->val));
            }
        }
        return false;
    }
};

解法3：BFS-层序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        //层序遍历
        if(root == nullptr) return false;
        queue<pair<TreeNode*,int>> que;
        que.push({root,root->val});
        while(!que.empty()){
            int size = que.size();
            
            pair<TreeNode*,int> node = que.front();
            que.pop();
            if(!node.first->left && !node.first->right && node.second == targetSum) return true;
            if(node.first->left) que.push({node.first->left,node.first->left->val + node.second});
            if(node.first->right) que.push({node.first->right,node.first->right->val + node.second});
            
        }
        return false;
    }
};

113. 路径总和 II

力扣链接
给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

提示：

树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

解法1：DFS-递归

思路：
113.路径总和ii要遍历整个树，找到所有路径，所以递归函数不要返回值！

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> result;
    vector<int> path;
     // 递归函数不需要返回值，因为我们要遍历整个树
    void traversal(TreeNode* cur, int sum){//遍历到当前节点cur时，还剩下多少sum
        if(!cur->right && !cur->left && sum == 0){
            result.push_back(path);
            return;
        }
        if(cur->left){
            path.push_back(cur->left->val);
            sum -= cur->left->val;
            traversal(cur->left, sum);
            sum += cur->left->val;
            path.pop_back();
        }
        if(cur->right){
            path.push_back(cur->right->val);
            sum -= cur->right->val;
            traversal(cur->right, sum);
            sum += cur->right->val;
            path.pop_back();
        }
    }
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        if(root == nullptr) return result;
        path.push_back(root->val);
        traversal(root, targetSum-root->val);
        return result;
    }
};

437. 路径总和 III

力扣链接
给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

提示:

二叉树的节点个数的范围是 [0,1000]
-109 <= Node.val <= 109
-1000 <= targetSum <= 1000

解法1：前缀和+递归

思路：

回溯的意义：
因为只有同一条路径上的节点间（节点和其某一祖先节点间）的前缀和做差才有意义。所以当前节点处理完之后，需要从map中移除这一个前缀和，然后再进入下一个分支路径。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<long long,int> umap;//前缀和-出现次数
    int pathSum(TreeNode* root, int targetSum) {
        umap[0] = 1;
        return dfs(root,0,targetSum);
    }
    //回溯
    int dfs(TreeNode* cur, long long preSum, int targetSum){
        if(!cur) return 0;
        long long curSum = preSum + cur->val;
        int cnt = 0;
        cnt += umap[curSum - targetSum];

        umap[curSum] += 1;
        cnt += dfs(cur->left,curSum,targetSum);//递归
        cnt += dfs(cur->right,curSum,targetSum);//递归
        //回溯
        umap[curSum] -= 1;//回到本层，恢复状态，去除当前节点的前缀和数量
        return cnt;
    }
};

时间复杂度：每个节点只遍历一次,O(N).

空间复杂度：开辟了一个hashMap,O(N).

解法2：DFS+二次递归

思路：

双重递归的操作，这种题目需要从每个节点开始进行类似的计算，所以第一个递归用来遍历这些节点，这二个递归用来处理这些节点，进行深度优先搜索。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int count = 0;
    //第二个递归，将所有的路径相加
    int pathSum(TreeNode* root, int targetSum) {
        if(!root) return 0;
        dfs(root,targetSum);
        pathSum(root->left, targetSum);
        pathSum(root->right, targetSum);
        return count;
    }
    //第一个递归，求出以每个节点为起始点的路径个数
    void dfs(TreeNode* root, int targetSum){
        if(!root) return;//终止条件
        if(targetSum - root->val == 0) count++;//中
        dfs(root->left, targetSum - root->val);//左
        dfs(root->right,targetSum - root->val);//右
    }
};

相似题目：129. 求根节点到叶节点数字之和

力扣链接
给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：

输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

示例 2：

输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

提示：

树中节点的数目在范围 [1, 1000] 内
0 <= Node.val <= 9
树的深度不超过 10

解法1：DFS-递归

思路：
深度优先搜索是很直观的做法。从根节点开始，遍历每个节点，如果遇到叶子节点，则将叶子节点对应的数字加到数字之和。如果当前节点不是叶子节点，则计算其子节点对应的数字，然后对子节点递归遍历。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int result = 0;
    int sumNumbers(TreeNode* root) {
        dfs(root,0);
        return result;
    }
    void dfs(TreeNode* cur, int num){
        if(!cur) return;
        //递归
        num = num*10 + cur->val;
        if(!cur->left && !cur->right){
            result += num;
        }
        dfs(cur->left,num);
        dfs(cur->right,num);
    }
};

隐含回溯的理解：

复杂度分析：

时间复杂度：O(n)，其中 n 是二叉树的节点个数。对每个节点访问一次。

空间复杂度：O(n)，其中 n 是二叉树的节点个数。空间复杂度主要取决于递归调用的栈空间，递归栈的深度等于二叉树的高度，最坏情况下，二叉树的高度等于节点个数，空间复杂度为 O(n)。

解法2：BFS-层序遍历

思路：

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int result = 0;
    int sumNumbers(TreeNode* root) {
        //层序遍历
        if(root == nullptr) return result;
        queue<pair<TreeNode*,int>> que;
        que.push(pair<TreeNode*,int>(root,root->val));
        while(!que.empty()){
            int size = que.size();
            for(int i = 0;i<size;i++){
                TreeNode* node = que.front().first;
                int num = que.front().second;
                que.pop();
                if(node->left == nullptr && node->right == nullptr) result += num;//中
                if(node->left) que.push(pair<TreeNode*,int>(node->left,num*10 + node->left->val));//左
                if(node->right) que.push(pair<TreeNode*,int>(node->right,num*10 + node->right->val));//右
            }
        }
        return result;
    }
};

相似题目：124. 二叉树中的最大路径和

力扣链接
路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

树中节点数目范围是 [1, 3 * 104]
-1000 <= Node.val <= 1000

解法1：递归

思路：

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxSum = INT_MIN;
    int maxPathSum(TreeNode* root) {
        dfs(root);
        return maxSum;
    }
    // dfs 返回以该节点为端点的最大路径和
    //后序遍历，需要处理左右子树传来的值
    int dfs(TreeNode* root){
        if(!root) return 0;
        //左
        int left = dfs(root->left);
        //右
        int right = dfs(root->right);
        //中
        int result = max(root->val, root->val + max(left,right));
        maxSum = max(maxSum, max(result,root->val + left + right));
        return result;
    }
};

257. 二叉树的所有路径

力扣链接
给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

输入：root = [1,2,3,null,5]
输出：[“1->2->5”,“1->3”]
示例 2：

输入：root = [1]
输出：[“1”]

提示：

树中节点的数目在范围 [1, 100] 内
-100 <= Node.val <= 100

解法1：递归

思路：
这道题目要求从根节点到叶子的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径。

在这道题目中将第一次涉及到回溯，因为我们要把路径记录下来，需要回溯来回退一一个路径在进入另一个路径。

前序遍历以及回溯的过程如图：

** 注意在函数定义的时候void traversal(TreeNode* cur, string path, vector& result) ，定义的是string path，每次都是复制赋值，不用使用引用，否则就无法做到回溯的效果。 **

那么在如上代码中，貌似没有看到回溯的逻辑，其实不然，回溯就隐藏在traversal(cur->left, path + “->”, result);中的 path + “->”。 每次函数调用完，path依然是没有加上"->" 的，这就是回溯了。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public://回溯
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> res;      
        string path;
        if(!root) return res;
        dfs(root,res,path);
        return res;
    }
    void dfs(TreeNode* root, vector<string>& res, string path){
        path += to_string(root->val);
        if(!root->left && !root->right){
            res.push_back(path);
            return;
        }
        path += "->";
        if(root->left){
            dfs(root->left,res,path);
        } 
        if(root->right){
            dfs(root->right,res,path);
        } 
    }
};

剑指 Offer 55 - I. 二叉树的深度

力扣链接
输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

例如：

给定二叉树 [3,9,20,null,null,15,7]，

3

/
9 20
/
15 7
返回它的最大深度 3 。

提示：

节点总数 <= 10000
注意：本题与主站 104 题相同：https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
二叉树最小深度

解法1：递归

思路：

本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。

而根节点的高度就是二叉树的最大深度，所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。

代码：

#include
#include
#include
#include
using namespace std;

struct TreeNode {
	int val;
	TreeNode* left;
	TreeNode* right;
	TreeNode() :val(0), left(nullptr), right(nullptr) {}
	TreeNode(int x) :val(x), left(nullptr), right(nullptr) {}
	TreeNode(int x, TreeNode* left, TreeNode* right) :val(x), left(left), right(right) {}
};

TreeNode* stringToTreeNode(string input) {
	input = input.substr(1, input.size() - 2);
	if (!input.size()) return nullptr;

	stringstream ss(input);
	string item;

	getline(ss, item, ',');
	TreeNode* root = new TreeNode(stoi(item));
	queue<TreeNode*> que;
	que.push(root);

	while (!que.empty()) {
		TreeNode* node = que.front();
		que.pop();

		if (!getline(ss, item, ',')) break;
		if (item != "null") {
			int leftNumber = stoi(item);
			node->left = new TreeNode(leftNumber);
			que.push(node->left);
		}

		if (!getline(ss, item, ',')) break;
		if (item != "null") {
			int rightNumber = stoi(item);
			node->right = new TreeNode(rightNumber);
			que.push(node->right);
		}
	}
	return root;
}

class Solution {
public:
	int maxDepth(TreeNode* root) {
		if (root == nullptr) return 0;
		return max(maxDepth(root->left), maxDepth(root->right)) + 1;
	}
};

int main() {
	string line;
	while (getline(cin, line)) {
		TreeNode* root = stringToTreeNode(line);
		int res = Solution().maxDepth(root);
		cout << to_string(res) << endl;
	}
	return 0;
}

解法2：层序遍历-迭代

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        //迭代 层序遍历
        if(!root) return 0;
        int depth = 0;
        queue<TreeNode*> que;
        que.push(root);

        while(!que.empty()){
            int size = que.size();
            depth++;
            for(int i = 0;i<size;i++){
                TreeNode* x = que.front();
                que.pop();
                if(x->left) que.push(x->left);
                if(x->right) que.push(x->right);
            }
        }
        return depth;
    }
};

相似题目：111. 二叉树的最小深度

力扣链接
给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：2
示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

树中节点数的范围在 [0, 105] 内
-1000 <= Node.val <= 1000

解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root == nullptr) return 0;
        else if(root->left == nullptr && root->right != nullptr) return minDepth(root->right) + 1;
        else if(root->left != nullptr && root->right == nullptr) return minDepth(root->left) + 1;

        return 1 + min(minDepth(root->left),minDepth(root->right));
    }
};

解法2：迭代

需要注意的是，只有当左右孩子都为空的时候，才说明遍历的最低点了。如果其中一个孩子为空则不是最低点

class Solution {
public:

    int minDepth(TreeNode* root) {
        if (root == NULL) return 0;
        int depth = 0;
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()) {
            int size = que.size();
            depth++; // 记录最小深度
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
                if (!node->left && !node->right) { // 当左右孩子都为空的时候，说明是最低点的一层了，退出
                    return depth;
                }
            }
        }
        return depth;
    }
};

662. 二叉树最大宽度

力扣链接
给定一个二叉树，编写一个函数来获取这个树的最大宽度。树的宽度是所有层中的最大宽度。这个二叉树与满二叉树（full binary tree）结构相同，但一些节点为空。

每一层的宽度被定义为两个端点（该层最左和最右的非空节点，两端点间的null节点也计入长度）之间的长度。

示例 1:

输入:

       1
     /   \
    3     2
   / \     \  
  5   3     9 

输出: 4
解释: 最大值出现在树的第 3 层，宽度为 4 (5,3,null,9)。
示例 2:

输入:

      1
     /  
    3    
   / \       
  5   3     

输出: 2
解释: 最大值出现在树的第 3 层，宽度为 2 (5,3)。
示例 3:

输入:

      1
     / \
    3   2 
   /        
  5      

输出: 2
解释: 最大值出现在树的第 2 层，宽度为 2 (3,2)。
示例 4:

输入:

      1
     / \
    3   2
   /     \  
  5       9 
 /         \
6           7

输出: 8
解释: 最大值出现在树的第 4 层，宽度为 8 (6,null,null,null,null,null,null,7)。
注意: 答案在32位有符号整数的表示范围内。

解法1：层序遍历

思路：
二叉树的位置索引标记如图，关键点：去掉任意的结点，不影响其他结点的位置索引
当前结点的位置索引假设为1，那左结点的位置索引为 1 x 2 + 1，右结点为 1 x 2 + 2

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int widthOfBinaryTree(TreeNode* root) {
        queue<pair<TreeNode*, long long>> que;
        int res = 0;
        if(!root) return 0;
        que.push({root,0});

        while(!que.empty()){
            res = max(res,(int)(que.back().second - que.front().second + 1));
            int size = que.size();
            int offset = que.front().second;
            for(int i = 0;i<size;i++){
                TreeNode* node = que.front().first;
                long long idx = que.front().second;
                que.pop();
                idx -= offset;// 缩小数值
                if(node->left) que.push({node->left, idx*2 + 1});
                if(node->right) que.push({node->right, idx*2 + 2});
            }
        }
        return res;
    }
};

剑指 Offer 55 - II. 平衡二叉树

力扣链接
输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

3

/
9 20
/
15 7
返回 true 。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

   1
  / \
 2   2
/ \

3 3
/
4 4
返回 false 。

限制：

0 <= 树的结点个数 <= 10000
注意：本题与主站 110 题相同：https://leetcode-cn.com/problems/balanced-binary-tree/

解法1：自底向上递归 后序遍历

思路：
既然要求比较高度，必然是要后序遍历。

递归三步曲分析：

1. 明确递归函数的参数和返回值
   参数：当前传入节点。
   返回值：以当前传入节点为根节点的树的高度。

那么如何标记左右子树是否差值大于1呢？

如果当前传入节点为根节点的二叉树已经不是二叉平衡树了，还返回高度的话就没有意义了。
所以如果已经不是二叉平衡树了，可以返回-1 来标记已经不符合平衡树的规则了。

代码如下：

// -1 表示已经不是平衡二叉树了，否则返回值是以该节点为根节点树的高度
int getHeight(TreeNode* node)

2. 明确终止条件
   递归的过程中依然是遇到空节点了为终止，返回0，表示当前节点为根节点的树高度为0

代码如下：

if (node == NULL) {
    return 0;
}

3. 明确单层递归的逻辑
   如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢？当然是其左子树高度和其右子树高度的差值。

分别求出其左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则则返回-1，表示已经不是二叉平衡树了。

代码如下：

int leftHeight = getHeight(node->left); // 左
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right); // 右
if (rightHeight == -1) return -1;

int result;
if (abs(leftHeight - rightHeight) > 1) {  // 中
    result = -1;
} else {
    result = 1 + max(leftHeight, rightHeight); // 以当前节点为根节点的树的最大高度
}

return result;

代码精简之后如下：

int leftHeight = getHeight(node->left);
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right);
if (rightHeight == -1) return -1;
return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);

此时递归的函数就已经写出来了，这个递归的函数传入节点指针，返回以该节点为根节点的二叉树的高度，如果不是二叉平衡树，则返回-1。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int depth(TreeNode* root){
        if(!root) return 0;
        int leftDepth = depth(root->left);
        int rightDepth = depth(root->right);
        if(leftDepth == -1 || rightDepth == -1) return -1;
        return abs(leftDepth - rightDepth) > 1 ? -1 : max(leftDepth,rightDepth) + 1;
    }
    bool isBalanced(TreeNode* root) {
        //自底向上递归 后序遍历
        return depth(root) == -1 ? false : true; 
    }
};

404. 左叶子之和

力扣链接
给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：

输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24
示例 2:

输入: root = [1]
输出: 0

提示:

节点数在 [1, 1000] 范围内
-1000 <= Node.val <= 1000

解法1：递归法

思路：
首先要注意是判断左叶子，不是二叉树左侧节点，所以不要上来想着层序遍历。

因为题目中其实没有说清楚左叶子究竟是什么节点，那么我来给出左叶子的明确定义：如果左节点不为空，且左节点没有左右孩子，那么这个节点的左节点就是左叶子

大家思考一下如下图中二叉树，左叶子之和究竟是多少？

其实是0，因为这棵树根本没有左叶子！

那么判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。

如果该节点的左节点不为空，该节点的左节点的左节点为空，该节点的左节点的右节点为空，则找到了一个左叶子，判断代码如下：

if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) {
    左叶子节点处理逻辑
}

递归的遍历顺序为后序遍历（左右中），是因为要通过递归函数的返回值来累加求取左叶子数值之和。

递归三部曲：

1. 确定递归函数的参数和返回值
   判断一个树的左叶子节点之和，那么一定要传入树的根节点，递归函数的返回值为数值之和，所以为int

使用题目中给出的函数就可以了。

2. 确定终止条件
   依然是

   if (root == NULL) return 0;

3. 确定单层递归的逻辑
   当遇到左叶子节点的时候，记录数值，然后通过递归求取左子树左叶子之和，和 右子树左叶子之和，相加便是整个树的左叶子之和。

代码如下：

int leftValue = sumOfLeftLeaves(root->left);    // 左
int rightValue = sumOfLeftLeaves(root->right);  // 右
                                                // 中
int midValue = 0;
if (root->left && !root->left->left && !root->left->right) {
    midValue = root->left->val;
}
int sum = midValue + leftValue + rightValue;
return sum;

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        //递归
        if(!root) return 0;
        int leftValue = sumOfLeftLeaves(root->left);
        int rightValue = sumOfLeftLeaves(root->right);
        int midValue = 0;
        if(root->left != nullptr && root->left->left == nullptr && root->left->right == nullptr){
            midValue += root->left->val;
        }
        return leftValue + rightValue + midValue;
    }
};

解法2：迭代法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        //迭代 前序遍历
        stack<TreeNode*> st;
        if(root) st.push(root);
        int res = 0;

        while(!st.empty()){
            TreeNode* node = st.top();
            st.pop();
            if(node->left && !node->left->left && !node->left->right) res += node->left->val;
            if(node->left) st.push(node->left);
            if(node->right) st.push(node->right);
        }
        return res;
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        //迭代
        stack<TreeNode*> st;
        if(!root) return 0;
        if(root) st.push(root);
        int mid = 0;

        while(!st.empty()){
            TreeNode* node = st.top();
            if(node){
                st.pop();
                st.push(node);
                st.push(nullptr);
                if(node->right) st.push(node->right);
                if(node->left) st.push(node->left);
            }else{
                st.pop();
                node = st.top();
                st.pop();
                if(node->left && !node->left->left && !node->left->right){
                    mid += node->left->val;
                }
            }
        }
        return mid;
    }
};

222. 完全二叉树的节点个数

力扣链接
给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

输入：root = [1,2,3,4,5,6]
输出：6
示例 2：

输入：root = []
输出：0
示例 3：

输入：root = [1]
输出：1

提示：

树中节点的数目范围是[0, 5 * 104]
0 <= Node.val <= 5 * 104
题目数据保证输入的树是 完全二叉树

进阶：遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗？

解法1：完全二叉树

（1）首先按照普通二叉树的逻辑来求。

这道题目的递归法和求二叉树的深度写法类似， 而迭代法，二叉树：层序遍历登场！ (opens new window)遍历模板稍稍修改一下，记录遍历的节点数量就可以了。

递归遍历的顺序依然是后序（左右中）。

（2）首先按照普通二叉树的逻辑来求。

这道题目的递归法和求二叉树的深度写法类似， 而迭代法，二叉树：层序遍历登场！ (opens new window)遍历模板稍稍修改一下，记录遍历的节点数量就可以了。

递归遍历的顺序依然是后序（左右中）。

完全二叉树（二）如图：

可以看出如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    //完全二叉树 递归
    int countNodes(TreeNode* root) {
       if(!root) return 0;
       TreeNode* left = root->left;
       TreeNode* right = root->right;
       int leftH = 0, rightH = 0;
       while(left){
           left = left->left;
           leftH++;
       }
       while(right){
           right = right->right;
           rightH++;
       }
       if(leftH == rightH){
           return (2<<leftH) - 1;
       }
       return countNodes(root->left) + countNodes(root->right) + 1;
    }
};

124. 二叉树中的最大路径和

力扣链接
路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6
示例 2：

输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

树中节点数目范围是 [1, 3 * 104]
-1000 <= Node.val <= 1000

解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxSum = INT_MIN;
    int dfs(TreeNode* root){// dfs 返回以该节点为端点的最大路径和
        if(root == nullptr) return 0;
        int left = dfs(root->left);//左
        int right = dfs(root->right);//右
        //中
        int tmp = max(root->val+max(left,right),root->val);//一个父节点只能和一个子节点相连
        maxSum = max(maxSum,max(tmp,root->val+left+right));
        return tmp;
    }
    int maxPathSum(TreeNode* root) {
        dfs(root);
        return maxSum;
    }
};

相似题目：543. 二叉树的直径

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

示例 :
给定二叉树

      1
     / \
    2   3
   / \     
  4   5    

返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

注意：两结点之间的路径长度是以它们之间边的数目表示。

解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int res = 0;
    int dfs(TreeNode* root){//以当前节点为端点的直径
        if(root->left == nullptr && root->right == nullptr) return 0;
        int left = root->left ? dfs(root->left) + 1 : 0;
        int right = root->right ? dfs(root->right) + 1 : 0;
        int tmp = max(left,right);
        res = max(left+right,res);
        return tmp;
    }
    int diameterOfBinaryTree(TreeNode* root) {
        dfs(root);
        return res;
    }
};

剑指 Offer 54. 二叉搜索树的第k大节点

力扣链接
给定一棵二叉搜索树，请找出其中第 k 大的节点的值。

示例 1:

输入: root = [3,1,4,null,2], k = 1
3
/
1 4

2
输出: 4
示例 2:

输入: root = [5,3,6,2,4,null,null,1], k = 3
5
/
3 6
/
2 4
/
1
输出: 4

限制：

1 ≤ k ≤ 二叉搜索树元素个数

解法1：逆中序遍历-递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int res = 0;
    int kthLargest(TreeNode* root, int k) {
        dfs(root,k);
        return res;
    }
    void dfs(TreeNode* root, int& k){//传引用 这里需要保证所有dfs函数共用一个k 
        if(root == NULL || k == 0) return;

        dfs(root->right,k);
        
        if(--k == 0){
            res = root->val;
            return;
        }
        dfs(root->left,k);
    }
};

572. 另一棵树的子树

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

示例 1：

输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true
示例 2：

输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出：false

提示：

root 树上的节点数量范围是 [1, 2000]
subRoot 树上的节点数量范围是 [1, 1000]
-104 <= root.val <= 104
-104 <= subRoot.val <= 104

解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSameTree(TreeNode* root1,TreeNode* root2){
        if(root1 == nullptr && root2 == nullptr) return true;
        else if(root1 == nullptr || root2 == nullptr) return false;
        else if(root1->val != root2->val) return false;

        return isSameTree(root1->left, root2->left) && isSameTree(root1->right,root2->right);
    }
    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        if(root == nullptr && subRoot == nullptr) return true;
        else if(root == nullptr || subRoot == nullptr) return false;
        if(root->val == subRoot->val && isSameTree(root, subRoot)){
            return true;
        }else{
            return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
        }
    }
};

||||||||||||||||||||||||二叉树的修改与改造||||||||||||||||||||||||

226. 翻转二叉树

力扣链接
翻转一棵二叉树。

示例：

备注:
这个问题是受到 Max Howell 的 原问题 启发的 ：

谷歌：我们90％的工程师使用您编写的软件(Homebrew)，但是您却无法在面试时在白板上写出翻转二叉树这道题，这太糟糕了。

解法1：递归DFS

思路：
（1）想要翻转它，其实就把每一个节点的左右孩子交换一下就可以了。

关键在于遍历顺序，前中后序应该选哪一种遍历顺序？注意只要把每一个节点的左右孩子翻转一下，就可以达到整体翻转的效果

这道题目使用前序遍历和后序遍历都可以，唯独中序遍历不方便，因为中序遍历会把某些节点的左右孩子翻转了两次！（未理解）

那么层序遍历可以不可以呢？依然可以的！只要把每一个节点的左右孩子翻转一下的遍历方式都是可以的！

（2）我们来看一下递归三部曲：

1.确定递归函数的参数和返回值
参数就是要传入节点的指针，不需要其他参数了，通常此时定下来主要参数，如果在写递归的逻辑中发现还需要其他参数的时候，随时补充。

返回值的话其实也不需要，但是题目中给出的要返回root节点的指针，可以直接使用题目定义好的函数，所以就函数的返回类型为TreeNode*。

TreeNode* invertTree(TreeNode* root)

2.确定终止条件
当前节点为空的时候，就返回

if (root == NULL) return root;

3.确定单层递归的逻辑
因为是先前序遍历，所以先进行交换左右孩子节点，然后反转左子树，反转右子树。

swap(root->left, root->right);
invertTree(root->left);
invertTree(root->right);

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        //递归
        //终止条件
        if(root == NULL) return root;

        swap(root->left,root->right); //中
        invertTree(root->left); //左
        invertTree(root->right); //右

        return root;
    }
};

解法2：迭代DFS

思路：

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        //迭代DFS
        stack<TreeNode*> ST;
        if(root != nullptr) ST.push(root);

        while(!ST.empty()){
            TreeNode* node = ST.top();
            if(node != nullptr){
                ST.pop();
                if(node->right) ST.push(node->right);
                if(node->left) ST.push(node->left);
                ST.push(node);
                ST.push(NULL);
            }else{
                ST.pop();
                node = ST.top();
                ST.pop();
                swap(node->left,node->right);
            }
        }
        return root;
    }
};

解法3：层序遍历BFS

思路：

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        //层序BFS
        queue<TreeNode*> Que;
        if(root != nullptr) Que.push(root);

        while(!Que.empty()){
            int size = Que.size();
            for(int i = 0;i<size;i++){
                TreeNode* node = Que.front();
                Que.pop();
                swap(node->left,node->right);
                if(node->left) Que.push(node->left);
                if(node->right) Que.push(node->right);
            }
        }
        return root;
    }
};

1104. 二叉树寻路

力扣链接
在一棵无限的二叉树上，每个节点都有两个子节点，树中的节点 逐行 依次按 “之” 字形进行标记。

如下图所示，在奇数行（即，第一行、第三行、第五行……）中，按从左到右的顺序进行标记；

而偶数行（即，第二行、第四行、第六行……）中，按从右到左的顺序进行标记。

给你树上某一个节点的标号 label，请你返回从根节点到该标号为 label 节点的路径，该路径是由途经的节点标号所组成的。

示例 1：

输入：label = 14
输出：[1,3,4,14]
示例 2：

输入：label = 26
输出：[1,2,6,10,26]

提示：

1 <= label <= 10^6

解法1：数学+二叉树

思路：

代码：

class Solution {
public:
    vector<int> pathInZigZagTree(int label) {
        vector<int> res;
        while(label){
            res.push_back(label);
            label /= 2;
        }
        reverse(res.begin(), res.end());
        int left, right , deepth = res.size();
        for(int i = 0;i<deepth;i++){
            if((deepth & 1) != (i & 1)) continue;
            left = (1 << i);
            right = 2* left - 1;
            res[i] = right - res[i] + left;
        }
        return res;
    }
};

106. 从中序与后序遍历序列构造二叉树

力扣链接
给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]
示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由 不同 的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历

解法1：递归

思路：

（1）我们可以发现后序遍历的数组最后一个元素代表的即为根节点。知道这个性质后，我们可以利用已知的根节点信息在中序遍历的数组中找到根节点所在的下标，然后根据其将中序遍历的数组分成左右两部分，左边部分即左子树，右边部分为右子树，针对每个部分可以用同样的方法继续递归下去构造。

（2）为了高效查找根节点元素在中序遍历数组中的下标，我们选择创建哈希表来存储中序序列，即建立一个（元素，下标）键值对的哈希表。

定义递归函数 helper(in_left, in_right) 表示当前递归到中序序列中当前子树的左右边界，递归入口为helper(0, n - 1) ：

1. 如果 in_left > in_right，说明子树为空，返回空节点。

2. 选择后序遍历的最后一个节点作为根节点。

3. 利用哈希表 O(1)O(1) 查询当根节点在中序遍历中下标为 index。从 in_left 到 index - 1 属于左子树，从 index + 1 到 in_right 属于右子树。

4. 根据后序遍历逻辑，递归创建右子树 helper(index + 1, in_right) 和左子树 helper(in_left, index - 1)。注意这里有需要先创建右子树，再创建左子树的依赖关系。可以理解为在后序遍历的数组中整个数组是先存储左子树的节点，再存储右子树的节点，最后存储根节点，如果按每次选择「后序遍历的最后一个节点」为根节点，则先被构造出来的应该为右子树。

5. 返回根节点 root。

注意：先构建右子树，要是先构建的是左子树还有个确定后序区间的步骤。inorder和postorder 的左子树要对应上。postorder每次pop末尾的值，构建完右子树刚好pop到了其左子树末尾。 因此不需要再单独找postorder的左子树末尾在哪里。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<int,int> umap;
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        int n = inorder.size();
        for(int i = 0;i<n;i++) umap[inorder[i]] = i;
        return dfs(inorder,0,n-1,postorder,0,n-1);
    }
    TreeNode* dfs(vector<int>& inorder, int in_start, int in_end,vector<int>& postorder, int post_start, int post_end){
        if(in_start > in_end || post_start > post_end) return nullptr;

        int rootValue = postorder[post_end];
        TreeNode* root = new TreeNode(rootValue);

        int inorder_root = umap[rootValue];
        int size_left_subtree = inorder_root - in_start;
        root->left = dfs(inorder,in_start,inorder_root-1,postorder,post_start,post_start + size_left_subtree-1);
        root->right = dfs(inorder,inorder_root + 1,in_end,postorder,post_start + size_left_subtree,post_end-1);
        
        return root;
    }
};

相似题目： 105. 从前序与中序遍历序列构造二叉树

力扣链接
给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证 为二叉树的前序遍历序列
inorder 保证 为二叉树的中序遍历序列

解法1：递归

思路：
（1）对于任意一颗树而言，前序遍历的形式总是

[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]

即根节点总是前序遍历中的第一个节点。而中序遍历的形式总是

[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]

只要我们在中序遍历中定位到根节点，那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的，因此我们就可以对应到前序遍历的结果中，对上述形式中的所有左右括号进行定位。

这样以来，我们就知道了左子树的前序遍历和中序遍历结果，以及右子树的前序遍历和中序遍历结果，我们就可以递归地对构造出左子树和右子树，再将这两颗子树接到根节点的左右位置。

（2）细节

在中序遍历中对根节点进行定位时，一种简单的方法是直接扫描整个中序遍历的结果并找出根节点，但这样做的时间复杂度较高。 我们可以考虑使用哈希表来帮助我们快速地定位根节点。对于哈希映射中的每个键值对，键表示一个元素（节点的值），值表示其在中序遍历中的出现位置。在构造二叉树的过程之前，我们可以对中序遍历的列表进行一遍扫描，就可以构造出这个哈希映射。在此后构造二叉树的过程中，我们就只需要 O(1) 的时间对根节点进行定位了。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<int,int> umap;//中序遍历 val-下标
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = inorder.size();
        for(int i = 0;i<n;i++){
            umap[inorder[i]] = i;
        }
        return dfs(preorder,0,n-1,inorder,0,n-1);
    }
    TreeNode* dfs(vector<int>& preorder, int pre_start, int pre_end,vector<int>& inorder, int in_start, int in_end){
        if(pre_start > pre_end || in_start > in_end){
            return nullptr;
        }
        int rootValue = preorder[pre_start];
        TreeNode* root = new TreeNode(rootValue);

        int inorder_root = umap[rootValue];//中序定位
        int size_left_subtree = inorder_root - in_start;
        root->left = dfs(preorder,pre_start+1,pre_start+size_left_subtree,inorder,in_start,inorder_root-1);
        root->right = dfs(preorder,pre_start+size_left_subtree+1,pre_end,inorder,inorder_root+1,in_end);
        return root;
    }
};

297. 二叉树的序列化与反序列化

力扣链接
序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

提示: 输入输出格式与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，你也可以采用其他的方法解决这个问题。

示例 1：

输入：root = [1,2,3,null,null,4,5]
输出：[1,2,3,null,null,4,5]
示例 2：

输入：root = []
输出：[]
示例 3：

输入：root = [1]
输出：[1]
示例 4：

输入：root = [1,2]
输出：[1,2]

提示：

树中结点数在范围 [0, 104] 内
-1000 <= Node.val <= 1000

解法1：

思路：

（1）根据二叉树的性质，通过（前序/后序/层序） + 中序遍历能够唯一确定一棵二叉树。其实还有一种方式，即带空节点的（前序/中序/后序）遍历也能唯一确定一棵二叉树。

（2）对二叉树进行前序遍历，序列化后的每个结点间用“，”分隔，空结点则用“null ”表示，在根据序列构造二叉树，难点在于整型和字符的转化。

时间复杂度：O(n)，n为结点个数。
空间复杂度：O(n)。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Codec {
public:

    void _serialize_(TreeNode* root, string& s){
        if(root == nullptr) s += "null,";
        else{
            s += to_string(root->val) + ",";
            _serialize_(root->left,s);
            _serialize_(root->right,s);
        }
    }

    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        string res;
        _serialize_(root, res);
        return res;
    }

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        queue<string> q;
        string s;
        for(char& c:data){
            if(c == ','){
                q.push(s);
                s.clear();
            }else{
                s+=c;
            }
        }
        if(!s.empty()){
            q.push(s);
            s.clear();
        }
        return dfs(q);
    }
    TreeNode* dfs(queue<string>& q){
        
        if(q.front() == "null"){
            q.pop();
            return nullptr;
        } 
        
        TreeNode* root = new TreeNode(stoi(q.front()));
        q.pop();
        root->left = dfs(q);
        root->right = dfs(q);
        return root;
        
    }
};

// Your Codec object will be instantiated and called as such:
// Codec ser, deser;
// TreeNode* ans = deser.deserialize(ser.serialize(root));

相似题目：剑指 Offer 37. 序列化二叉树

力扣链接
请实现两个函数，分别用来序列化和反序列化二叉树。

你需要设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

提示：输入输出格式与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，你也可以采用其他的方法解决这个问题。

示例：

输入：root = [1,2,3,null,null,4,5]
输出：[1,2,3,null,null,4,5]

注意：本题与主站 297 题相同：https://leetcode-cn.com/problems/serialize-and-deserialize-binary-tree/

解法1：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Codec {
public:
    //前序遍历
    void serialize_helper(TreeNode* root, string& res){
        if(!root){
            res += "null,";
        }else{
            res += to_string(root->val) + ",";
            serialize_helper(root->left, res);
            serialize_helper(root->right, res);
        }
    }
    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        string res;
        serialize_helper(root, res);
        return res;
    }

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        //使用队列将字符串转化为数字，一个原因是字符串不改变相对顺序
        queue<string> que;
        string s;
        for(char& c:data){
            if(c == ','){
                que.push(s);
                s.clear();
            }else{
                s += c;
            }
        }
        if(!s.empty()){
            que.push(s);
            s.clear();
        }
        return deserialize_helper(que);
    }

    TreeNode* deserialize_helper(queue<string>& que){
        if(que.front() == "null"){
            que.pop();
            return nullptr;
        }

        TreeNode* root = new TreeNode(stoi(que.front()));
        que.pop();
        root->left = deserialize_helper(que);
        root->right = deserialize_helper(que);
        return root;
    }
};

// Your Codec object will be instantiated and called as such:
// Codec codec;
// codec.deserialize(codec.serialize(root));

相似题目：449. 序列化和反序列化二叉搜索树

力扣链接
序列化是将数据结构或对象转换为一系列位的过程，以便它可以存储在文件或内存缓冲区中，或通过网络连接链路传输，以便稍后在同一个或另一个计算机环境中重建。

设计一个算法来序列化和反序列化 二叉搜索树 。 对序列化/反序列化算法的工作方式没有限制。 您只需确保二叉搜索树可以序列化为字符串，并且可以将该字符串反序列化为最初的二叉搜索树。

编码的字符串应尽可能紧凑。

示例 1：

输入：root = [2,1,3]
输出：[2,1,3]
示例 2：

输入：root = []
输出：[]

提示：

树中节点数范围是 [0, 104]
0 <= Node.val <= 104
题目数据 保证 输入的树是一棵二叉搜索树。

解法1：

思路：
直接将其用先序遍历序列化，因为是二叉搜索树，所以排序后就是中序遍历，因此反序列化就转换成了105题的从先序与中序构造二叉树的问题。
代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Codec {
public:
    void serialize_helper(TreeNode* root, string& s){
        if(root == nullptr) s += "";
        else{
            s += to_string(root->val) + ',';
            serialize_helper(root->left,s);
            serialize_helper(root->right,s);
        }
    }
    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        string res;
        serialize_helper(root,res);
        return res;
    }
    TreeNode* deserialize_helper(int in_left, int in_right, vector<int>& preorder, vector<int>& inorder){
        if(in_left > in_right) return nullptr;
        int rootValue = preorder[pre_idx];
        TreeNode* root = new TreeNode(rootValue);

        int in_idx = idx_map[rootValue];
        pre_idx++;
        root->left = deserialize_helper(in_left,in_idx-1,preorder,inorder);
        root->right = deserialize_helper(in_idx+1,in_right,preorder,inorder);
        return root;
    }
    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        vector<int> preorder;
        string s;
        for(auto& c:data){
            if(c == ','){
                preorder.push_back(stoi(s));
                s.clear();
            }else{
                s += c;
            }
        }
        if(!s.empty()){
            preorder.push_back(stoi(s));
            s.clear();
        }
        vector<int> inorder = preorder;
        sort(inorder.begin(),inorder.end());

        pre_idx = 0;
        int idx = 0;
        for(auto& x:inorder){
            idx_map[x] = idx++;
        }

        return deserialize_helper(0,inorder.size()-1,preorder,inorder);
    }
};

// Your Codec object will be instantiated and called as such:
// Codec* ser = new Codec();
// Codec* deser = new Codec();
// string tree = ser->serialize(root);
// TreeNode* ans = deser->deserialize(tree);
// return ans;

复杂度分析：

时间复杂度：序列化和反序列化都使用了O(N) 的时间。
空间复杂度：O(N)，存储了整个树。

114. 二叉树展开为链表

力扣链接
给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]
示例 2：

输入：root = []
输出：[]
示例 3：

输入：root = [0]
输出：[0]

提示：

树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void flatten(TreeNode* root) {
        //递归
        if(root == nullptr) return;
        flatten(root->left);
        flatten(root->right);
        TreeNode* tmp = root->right;
        root->right = root->left;
        root->left = nullptr;
        while(root->right) root = root->right;
        root->right = tmp;
    }
};

701. 二叉搜索树中的插入操作

力扣链接
给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

示例 1：

输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：

示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]
示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

提示：

树中的节点数将在 [0, 104]的范围内。
-108 <= Node.val <= 108
所有值 Node.val 是 独一无二 的。
-108 <= val <= 108
保证 val 在原始BST中不存在。

解法1：递归

思路：

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if(root == nullptr){
            TreeNode* root = new TreeNode(val);
            return root;
        }
        if(val < root->val) root->left = insertIntoBST(root->left,val);
        if(val > root->val) root->right = insertIntoBST(root->right,val);
        return root;
    }
};

解法2：迭代

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        //迭代
        if(root == nullptr){
            TreeNode* root = new TreeNode(val);
            return root;
        }
        TreeNode* pre = nullptr;
        TreeNode* cur = root;
        while(cur){
            pre = cur;
            if(val < cur->val) cur = cur->left;
            else cur = cur->right;
        }
        TreeNode* node = new TreeNode(val);
        if(val < pre->val) pre->left = node;
        else pre->right = node;
        return root;
    }
};

||||||||||||||||||||||||||求二叉搜索树的属性|||||||||||||||||||||||||

700. 二叉搜索树中的搜索

likou
给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

示例 1:

输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]
Example 2:

输入：root = [4,2,7,1,3], val = 5
输出：[]

提示：

数中节点数在 [1, 5000] 范围内
1 <= Node.val <= 107
root 是二叉搜索树
1 <= val <= 107

解法1：迭代

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        //迭代
        while(root){
            if(root->val > val) root = root->left;
            else if(root->val < val) root = root->right;
            else return root;
        }
        return nullptr;
    }
};

解法2：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(root == nullptr) return nullptr;
        if(root->val > val){
            return searchBST(root->left, val);
        }else if(root->val < val){
            return searchBST(root->right, val);
        }else{
            return root;
        }

    }
};

98. 验证二叉搜索树

likou
给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true
示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1

解法1：迭代法

代码随想录

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    //定义一个全局变量，用来比较遍历的节点是否有序
    TreeNode* pre = NULL;
    bool isValidBST(TreeNode* root) {
        if (root == NULL) return true;
        stack<TreeNode*> ST;
        TreeNode* pre = NULL;//记录前一个节点
        ST.push(root);
        while (!ST.empty()){
            TreeNode* node = ST.top();
            if (node != NULL){
                ST.pop();
                if (node->right) ST.push(node->right);
                ST.push(node);
                ST.push(NULL);
                if (node->left) ST.push(node->left);
            }else{
                ST.pop();
                node = ST.top();
                ST.pop();
                if (pre != NULL){
                    if (pre->val >= node->val) return false;
                }
                pre = node;
            }

        }
        return true;
    }
};

解法2：递归法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* pre = nullptr;
    bool isValidBST(TreeNode* root) {
        if(!root) return true;
        bool left = isValidBST(root->left);
        if(pre && pre->val >= root->val) return false;
        pre = root;
        bool right = isValidBST(root->right);
        return left && right;
    }
};

530. 二叉搜索树的最小绝对差

力扣链接
给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

示例 1：

输入：root = [4,2,6,1,3]
输出：1
示例 2：

输入：root = [1,0,48,null,null,12,49]
输出：1

提示：

树中节点的数目范围是 [2, 104]
0 <= Node.val <= 105

注意：本题与 783 https://leetcode-cn.com/problems/minimum-distance-between-bst-nodes/ 相同

解法1：递归

题目中要求在二叉搜索树上任意两节点的差的绝对值的最小值。

注意是二叉搜索树，二叉搜索树可是有序的。

遇到在二叉搜索树上求什么最值啊，差值之类的，就把它想成在一个有序数组上求最值，求差值，这样就简单多了。

把二叉搜索树转化为有序数组了，其实在二叉搜素树中序遍历的过程中，我们就可以直接计算了。

需要用一个pre节点记录一下cur节点的前一个节点。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int res = INT_MAX;
    TreeNode* pre = nullptr;
    void dfs(TreeNode* root){
        if(root == nullptr) return;
        dfs(root->left);

        if(pre){
            res = min(res,abs(pre->val - root->val));
        }
        pre = root;

        dfs(root->right);
    }
    int getMinimumDifference(TreeNode* root) {
        dfs(root);
        return res;
    }
};

相似题目：501. 二叉搜索树中的众数

力扣链接
给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有 众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树

示例 1：

输入：root = [1,null,2,2]
输出：[2]
示例 2：

输入：root = [0]
输出：[0]

提示：

树中节点的数目在范围 [1, 104] 内
-105 <= Node.val <= 105

进阶：你可以不使用额外的空间吗？（假设由递归产生的隐式调用栈的开销不被计算在内）

解法1：哈希表+排序

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    //遍历 用哈希表记录频率
    void dfs(TreeNode* root, unordered_map<int,int>& umap){
        if(root == nullptr) return;
        umap[root->val]++;
        dfs(root->left,umap);
        dfs(root->right,umap);
    }
    vector<int> findMode(TreeNode* root) {
        unordered_map<int,int> umap;
        vector<int> res;
        if(root == nullptr) return res;
        dfs(root,umap);

        vector<pair<int,int>> vec(umap.begin(),umap.end());
        sort(vec.begin(),vec.end(),[&](const pair<int,int>& a, const pair<int,int>& b){
            return a.second > b.second;
        });
        res.push_back(vec[0].first);
        for(int i = 1;i<vec.size();i++){
            if(vec[i].second == vec[0].second) res.push_back(vec[i].first);
        }
        return res;
    }
};

解法2：递归

既然是搜索树，它中序遍历就是有序的。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int cnt = 0;
    int maxCnt = 0;
    vector<int> res;
    TreeNode* pre = nullptr;
    //中序遍历是有序数组
    void dfs(TreeNode* root){
        if(root == nullptr) return;
        dfs(root->left);

        if(pre == nullptr){
            cnt = 1;
        }else if(pre->val == root->val){
            cnt++;
        }else{
            cnt = 1;
        }
        pre = root;

        if(cnt == maxCnt){
            res.push_back(root->val);
        }
        if(cnt > maxCnt){
            maxCnt = cnt;
            res.clear();
            res.push_back(root->val);
        }

        dfs(root->right);
    }
    vector<int> findMode(TreeNode* root) {
        dfs(root);
        return res;
    }
};

538. 把二叉搜索树转换为累加树

力扣链接
给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。
注意：本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

示例 1：

输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2：

输入：root = [0,null,1]
输出：[1,null,1]
示例 3：

输入：root = [1,0,2]
输出：[3,3,2]
示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

提示：

树中的节点数介于 0 和 104 之间。
每个节点的值介于 -104 和 104 之间。
树中的所有值 互不相同 。
给定的树为二叉搜索树。

解法1：逆中序遍历

BST的中序遍历就是从小到大,那么反过来就是从大到小,然后累加就好了.
代码随想录

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    //递归
   TreeNode* pre;//记录前一个节点的数值
   void traversal(TreeNode* root){
        if (root == nullptr) return;
        if (root->right) traversal(root->right);//右
        if (pre != nullptr)
            root->val += pre->val;
        pre = root;
        if (root->left) traversal(root->left);//左
        
    }
    TreeNode* convertBST(TreeNode* root) {
        pre = nullptr;
        traversal(root);
        return root;
    }
};

||||||||||||||||||||||||||二叉树公共祖先问题|||||||||||||||||||||||||

236. 二叉树的最近公共祖先

力扣链接
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

树中节点数目在范围 [2, 105] 内。
-109 <= Node.val <= 109
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。

解法1：二叉树+DFS

思路：
参考代码随想录
代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //递归
        if (root == p || root == q || root == NULL) return root;
        //左
        TreeNode* leftT = lowestCommonAncestor(root->left,p,q);
        //右
        TreeNode* rightT = lowestCommonAncestor(root->right,p,q);
        //中
        if (leftT != NULL && rightT != NULL) return root;
        else if (leftT == NULL && rightT != NULL) return rightT;
        else if (leftT != NULL && rightT == NULL) return leftT;
        else {
            return NULL;
        }
        
    }
};

235. 二叉搜索树的最近公共祖先

力扣链接
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。

解法1：二叉树+递归

思路：

代码：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root->val > p->val && root->val > q->val) {
            return lowestCommonAncestor(root->left, p, q);
        } else if (root->val < p->val && root->val < q->val) {
            return lowestCommonAncestor(root->right, p, q);
        } else return root;
    }
};

解法2：二叉树+迭代

思路：

代码：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        while(root) {
            if (root->val > p->val && root->val > q->val) {
                root = root->left;
            } else if (root->val < p->val && root->val < q->val) {
                root = root->right;
            } else return root;
        }
        return NULL;
    }
};

||||||||||||||||||||||二叉搜索树的修改与改造|||||||||||||||||||||

剑指 Offer 07. 重建二叉树

力扣链接
输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

限制：

0 <= 节点个数 <= 5000

注意：本题与主站 105 题重复：https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/

解法1：递归

思路：
二叉树前序遍历的顺序为：

先遍历根节点；

随后递归地遍历左子树；

最后递归地遍历右子树。

二叉树中序遍历的顺序为：

先递归地遍历左子树；

随后遍历根节点；

最后递归地遍历右子树。

在「递归」地遍历某个子树的过程中，我们也是将这颗子树看成一颗全新的树，按照上述的顺序进行遍历。挖掘「前序遍历」和「中序遍历」的性质，我们就可以得出本题的做法。

方法一：递归

对于任意一颗树而言，前序遍历的形式总是

[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]

即根节点总是前序遍历中的第一个节点。而中序遍历的形式总是

[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]

只要我们在中序遍历中定位到根节点，那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的，因此我们就可以对应到前序遍历的结果中，对上述形式中的所有左右括号进行定位。

这样以来，我们就知道了左子树的前序遍历和中序遍历结果，以及右子树的前序遍历和中序遍历结果，我们就可以递归地对构造出左子树和右子树，再将这两颗子树接到根节点的左右位置。

细节：

在中序遍历中对根节点进行定位时，一种简单的方法是直接扫描整个中序遍历的结果并找出根节点，但这样做的时间复杂度较高。我们可以考虑使用哈希表来帮助我们快速地定位根节点。对于哈希映射中的每个键值对，键表示一个元素（节点的值），值表示其在中序遍历中的出现位置。在构造二叉树的过程之前，我们可以对中序遍历的列表进行一遍扫描，就可以构造出这个哈希映射。在此后构造二叉树的过程中，我们就只需要 O(1)的时间对根节点进行定位了。

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
private:
    unordered_map<int,int> inorder_map;
public:
    TreeNode* helper(const vector<int>& preorder, const vector<int>& inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right){
        if(preorder_left > preorder_right || inorder_left > inorder_right) return nullptr;
        int preorder_root_idx = preorder_left;  // 前序遍历中的第一个节点就是根节点
        int inorder_root_idx = inorder_map[preorder[preorder_root_idx]];// 在中序遍历中定位根节点

        TreeNode* root = new TreeNode(preorder[preorder_root_idx]);// 在中序遍历中定位根节点
        int left_subtree_sz = inorder_root_idx - inorder_left; // 得到左子树中的节点数目

        root->left = helper(preorder,inorder,preorder_left+1,preorder_left+left_subtree_sz,inorder_left,inorder_root_idx-1);
        root->right = helper(preorder,inorder,preorder_left+left_subtree_sz+1,preorder_right,inorder_root_idx+1,inorder_right);
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = preorder.size();
        for(int i = 0;i<n;i++) inorder_map[inorder[i]] = i; // 得到左子树中的节点数目
        return helper(preorder, inorder, 0, n-1, 0, n-1);
    }
};

108. 将有序数组转换为二叉搜索树

力扣链接
给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：

输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 按 严格递增 顺序排列

解法1：二叉搜索树+DFS+分治

思路：

题目中说要转换为一棵高度平衡二叉搜索树。这和转换为一棵普通二叉搜索树有什么差别呢？

其实这里不用强调平衡二叉搜索树，数组构造二叉树，构成平衡树是自然而然的事情，因为大家默认都是从数组中间位置取值作为节点元素，一般不会随机取，所以想构成不平衡的二叉树是自找麻烦。

本质就是寻找分割点，分割点作为当前节点，然后递归左区间和右区间。

因为有序数组构造二叉搜索树，寻找分割点就比较容易了。

分割点就是数组中间位置的节点。

那么为问题来了，如果数组长度为偶数，中间节点有两个，取哪一个？

取哪一个都可以，只不过构成了不同的平衡二叉搜索树。
代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* dfs(vector<int>& nums, int left, int right){
        if(left > right) return nullptr;
        int mid = left + (right - left) / 2;
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = dfs(nums,left,mid-1);
        root->right = dfs(nums,mid+1,right);
        return root;
    }
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        TreeNode* root = dfs(nums,0,nums.size()-1);
        return root;
    }
};

相似题目：109. 有序链表转换二叉搜索树

力扣链接
给定一个单链表，其中的元素按升序排序，将其转换为高度平衡的二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

给定的有序链表： [-10, -3, 0, 5, 9],

一个可能的答案是：[0, -3, 9, -10, null, 5], 它可以表示下面这个高度平衡二叉搜索树：

  0
 / \

-3 9
/ /
-10 5

解法1：链表转数组+二叉搜索树

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* dfs(vector<int>& vec,int left, int right){
        if(left > right) return nullptr;
        int mid = left + (right - left)/2;
        TreeNode* root = new TreeNode(vec[mid]);
        root->left = dfs(vec, left, mid-1);
        root->right = dfs(vec, mid + 1,right);
        return root;
    }
    TreeNode* sortedListToBST(ListNode* head) {
        vector<int> vec;
        ListNode* p = head;
        while(p!=nullptr){
            vec.push_back(p->val);
            p = p->next;
        }
        return dfs(vec,0,vec.size()-1);
    }
};

解法2：链表+二叉搜索树+分治

思路：

a) 用两个指针，一块一慢，快的每次走两步，慢的每次走一步.这样当快指针遍历结束时，慢指针指向的也就是链表的中间位置。这时候把中间位置的结点的值作为二叉搜索树当前结点的值.

b)递归+快慢指针法。不用断开链表，分别用head和tail定义链首和链尾，链表区间为左闭右开，即 [ head , tail ）。

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* dfs(ListNode* head, ListNode* tail){
        if(head == tail ) return nullptr;

        ListNode* fast = head;
        ListNode* slow = head;
        while(fast != tail && fast->next != tail){
            slow = slow->next;
            fast = fast->next->next;
        }
        TreeNode* root = new TreeNode(slow->val);
        root->left = dfs(head, slow);
        root->right = dfs(slow->next,tail);
        return root;
    }
    TreeNode* sortedListToBST(ListNode* head) {
        if(head == nullptr) return nullptr;
        return dfs(head,nullptr);
    }
};

617. 合并二叉树

力扣链接
给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：

输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]
示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

提示：

两棵树中的节点数目在范围 [0, 2000] 内
-104 <= Node.val <= 104

解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        //递归 同时操作两棵树
        if (root1 == NULL) return root2;//终止条件
        if (root2 == NULL) return root1;
        root1->val += root2->val;//中

        //
        root1->left = mergeTrees(root1->left,root2->left);//左
        root1->right = mergeTrees(root1->right,root2->right);//右

        return root1;
    }
};

669. 修剪二叉搜索树

力扣链接
给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

示例 2：

输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

提示：

树中节点数在范围 [1, 104] 内
0 <= Node.val <= 104
树中每个节点的值都是 唯一 的
题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 104

解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        //
        if(root == nullptr) return nullptr;
        if(root->val < low) return trimBST(root->right,low,high);//范围左
        else if(root->val > high) return trimBST(root->left,low,high);//范围右
        else{//范围内
            root->left = trimBST(root->left,low,high);
            root->right = trimBST(root->right,low,high);
        }
        return root;
    }
};

450. 删除二叉搜索树中的节点

力扣链接
给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；
如果找到了，删除它。

示例 1:

输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:

输入: root = [], key = 0
输出: []

提示:

节点数的范围 [0, 104].
-105 <= Node.val <= 105
节点值唯一
root 是合法的二叉搜索树
-105 <= key <= 105

解法1: 递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if(root == nullptr) return nullptr;
        if(key < root->val) root->left = deleteNode(root->left, key);
        else if(key > root->val) root->right = deleteNode(root->right, key);
        else{
            if(root->left == nullptr) return root->right;
            else if(root->right == nullptr) return root->left;
            else if(root->left != nullptr && root->right != nullptr){
                TreeNode* node = root->right;
                while(node->left){
                    node = node->left;
                }
                node->left = root->left;
                root = root->right;
            }
        }
        return root;
    }
};

96. 不同的二叉搜索树

力扣链接
给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

输入：n = 3
输出：5
示例 2：

输入：n = 1
输出：1

提示：

1 <= n <= 19

解法1：动态规划

结题思路：假设n个节点存在二叉排序树的个数是G(n)，1为根节点，2为根节点，…，n为根节点，当1为根节点时，其左子树节点个数为0，右子树节点个数为n-1，同理当2为根节点时，其左子树节点个数为1，右子树节点为n-2，所以可得G(n) = G(0)G(n-1)+G(1)(n-2)+…+G(n-1)*G(0)

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n+1,0);
        dp[0] = 1;
        for(int i = 1;i<=n;i++){
            for(int j = 1;j<=i;j++){
                dp[i] += dp[i-j]* dp[j-1];
            }
        }
        return dp[n];
    }
};

相似题目：95. 不同的二叉搜索树 II

力扣链接
给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。

示例 1：

输入：n = 3
输出：[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]
示例 2：

输入：n = 1
输出：[[1]]

提示：

1 <= n <= 8

解法1：回溯

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:

    vector<TreeNode*> generateTrees(int n) {
        return dfs(1,n);
    }
    vector<TreeNode*> dfs(int start, int end){
        vector<TreeNode*> res;
        if(start > end){
            res.push_back(nullptr);
        }
        for(int i = start;i<=end;i++){
            vector<TreeNode*> l = dfs(start,i-1);
            vector<TreeNode*> r = dfs(i+1,end);
            for(auto ll:l){
                for(auto rr:r){
                    TreeNode* root = new TreeNode(i);
                    root->left = ll;
                    root->right = rr;
                    res.push_back(root);
                }
            }
        }
        return res;
    }
};