算法学习（10）：LeetCode刷题之Dijkstra最短路径算法

前言：

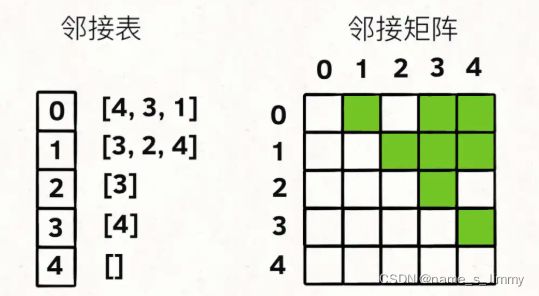
迪杰斯特拉(Dijkstra)最短路径算法是求有向加权图中某个节点到其他节点的最短路径。“图”这种数据结构的具体实现就是“邻接矩阵”或者“邻接表”。

比如上面这个图，用邻接表或者邻接矩阵的存储方式如下，图中的节点一般抽象成一个数字（即下标或索引）：

首先，我们来确定一下Dijkstra算法的签名：

// 输入一个起点和一个图（邻接矩阵表示），返回start到其他节点的最短路径，节点的值作为返回数组的下标
int[] dijkstra(int start, int[][] graph)

最短路径算法的思路可以由BFS算法进行扩展，之前我们学习过二叉树的层序遍历和网格型BFS的方法，BFS其实就是while循环里面套for循环。其中while循环控制一层一层往下走，for循环控制遍历每一层的节点。BFS算法处理的是无权图的搜索问题，所谓无权图，可以认为每条边的权重是1，从start起点到任意一个节点之间的路径权重就是它们之间“边”的条数。但是到了加权图这里，情况就变了，可能从start到end只需要走一步，但是这1步权重特别大，最短的路径其实要走很多步。如下图，0到4可以走红色的线，但是权重很大，实际上最短路径因该是绿色的4条路径加起来的权重。

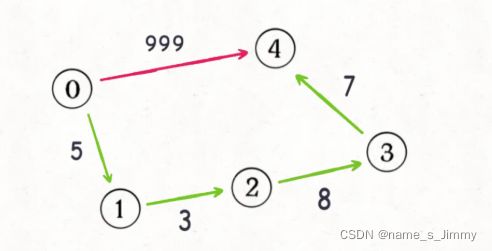
那么，我们怎么利用BFS算法改造成Dijkstra算法呢？即想办法去掉while循环中的for循环。 为什么呢？for循环控制着每一层的节点遍历，并且将下一层的节点放入到队列中以备下一层循环，即for循环控制着层数depth的累加。但是在加权图的最短路径问题上，层数depth已经没有意义了，路径的权重之和才有意义，所以这个for循环要想办法去掉，引入别的比较方式。

正文

1、Dijkstra算法框架

首先，我们要根据题目条件，构造出图的表示（邻接矩阵或者邻接表），这里我用了比较好理解的临界矩阵，即二维数组graph[][]。

其次，我们还需要一个辅助类，来记录从起点start到当前节点的距离。

class Node {
    // 图节点的 id
    int id;
    // 从 start 节点到当前节点的距离
    int distFromStart;

    State(int id, int distFromStart) {
        this.id = id;
        this.distFromStart = distFromStart;
    }
}

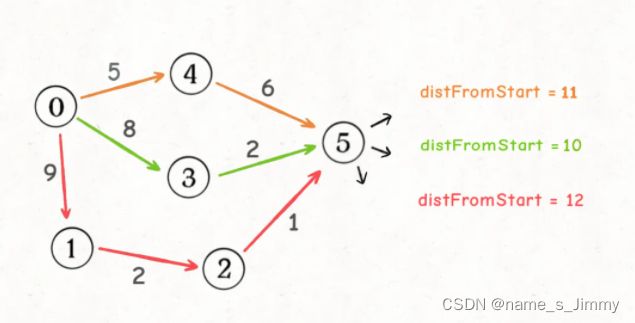
在BFS算法中，由于是无权图，那么第一次遇到某个节点时所走的步数就是最短距离，所以使用一个visited数组防止走回头路，每个节点只会经过一次。但是在加权图中则不同，当第一次经过某个节点时，所走过的路径权重之和，不一定就是最小的，所以对于同一个节点，可能会经过多次，而且每次的权重和可能都不一样。如下图，节点5会经过3次，每次的distFromStart都不一样，取最小的那个就是最终的答案。

2、LeetCode No.743 网络延迟时间

接下来，我们以LeetCode第743题【网络延迟时间】为例，来讲解Dijkstra算法的具体实现。

有 n 个网络节点，标记为 1 到 n。

给你一个列表 times，表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。
现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。

直接上代码：

// Node类记录start到每个节点的距离
class Node {
    int id;
    int distFromStart;

    public Node(int id, int distFromStart) {
        this.id = id;
        this.distFromStart = distFromStart;
    }
}
class Solution {
    public int networkDelayTime(int[][] times, int n, int k) {
    	// 1、构造图的邻接矩阵表示
        int[][] graph = new int[n + 1][n + 1];
        for (int i = 0; i < graph.length; i++) {
            Arrays.fill(graph[i], -1);
        }

        for (int i = 0; i < times.length; i++) {
            graph[times[i][0]][times[i][1]] = times[i][2];
        }

		// k即start起始点，得到start到每个节点的最短距离
        int[] tmp = dijkstra(k, graph);
        int ret = 0;
        // 遍历结果数组，找出最大值即答案
        for (int i = 1; i < tmp.length; i++) {
            if (tmp[i] == Integer.MAX_VALUE) {
                return -1;
            }
            // System.out.println(tmp[i] + ","); 调试
            if (tmp[i] > ret) {
                ret = tmp[i];
            }
        }
        return ret;
    }
	// 最短路径算法模板
    private int[] dijkstra(int start, int[][] graph) {
	    // 记录最短路径的权重，你可以理解为 dp table
	    // 定义：ret[i] 的值就是节点 start 到达节点 i 的最短路径权重
        int[] ret = new int[graph.length];
        // 求最小值，所以 dp table 初始化为正无穷
        Arrays.fill(ret, Integer.MAX_VALUE);
        // base case，start 到 start 的最短距离就是 0
        ret[start] = 0;
		// 优先级队列，distFromStart 较小的排在前面
        PriorityQueue<Node> queue = new PriorityQueue<>(new Comparator<Node>() {
            @Override
            public int compare(Node o1, Node o2) {
                return o1.distFromStart - o2.distFromStart;
            }
        });
        // 从起点 start 开始进行 BFS
        queue.offer(new Node(start, 0));
        while (!queue.isEmpty()) {
            Node curNode = queue.poll();
            int curNodeId = curNode.id;
            int curNodeDistFromStart = curNode.distFromStart;
            // 将 curNode 的相邻节点装入队列
            for (Integer nextNodeId : getNextNode(curNodeId, graph)) {
            	// 看看从 curNode 达到 nextNode 的距离是否会更短
                int nextNodeDistFromStart = curNodeDistFromStart + graph[curNodeId][nextNodeId];
                if (nextNodeDistFromStart < ret[nextNodeId]) {
                	// 是的话，将这个节点以及距离放入队列
                    queue.offer(new Node(nextNodeId, nextNodeDistFromStart));
                    // 更新 dp table
                    ret[nextNodeId] = nextNodeDistFromStart;
                }
            }
        }
        return ret;
    }
	// 找当前阶段的相邻节点
    private List<Integer> getNextNode(int curNodeId, int[][] graph) {
        List<Integer> list = new ArrayList<>();
        for (int i = 0; i < graph.length; i++) {
            if (graph[curNodeId][i] != -1) {
                list.add(i);
            }
        }
        return list;
    }
}

相较于BFS算法，思考2个问题？
1、没有visited集合记录已访问的节点，所以一个节点会被访问多次，会被多次加入队列，那会不会导致队列永远不为空，造成死循环？

循环结束的条件是队列为空，那么你就要注意看什么时候往队列里放元素（调用offer）方法，再注意看什么时候从队列往外拿元素（调用poll方法）。while循环每执行一次，都会往外拿一个元素，但想往队列里放元素，可就有很多限制了，必须满足下面这个条件：

// 看看从 curNode 达到 nextNode 的距离是否会更短
int nextNodeDistFromStart = curNodeDistFromStart + graph[curNodeId][nextNodeId];
if (nextNodeDistFromStart < ret[nextNodeId]) {
	// 是的话，将这个节点以及距离放入队列
	queue.offer(new Node(nextNodeId, nextNodeDistFromStart));
	// 更新 dp table
	ret[nextNodeId] = nextNodeDistFromStart;
}

如果你能让到达nextNodeID的距离更短，那就更新distTo[nextNodeID]的值，让你入队，否则的话对不起，不让入队。因为两个节点之间的最短距离（路径权重）肯定是一个确定的值，不可能无限减小下去，所以队列一定会空，队列空了之后，distTo数组中记录的就是从start到其他节点的最短距离。

2、为什么用优先级队列PriorityQueue而不是LinkedList实现的普通队列？为什么要按照distFromStart的值来排序？

Dijkstra 算法使用优先级队列，主要是为了效率上的优化，类似一种贪心算法的思路。如果你非要用普通队列，其实也没问题的，你可以直接把PriorityQueue改成LinkedList，也能得到正确答案，但是效率会低很多。

为什么说是一种贪心思路呢，比如说下面这种情况，你想计算从起点start到终点end的最短路径权重：

你下一步想遍历那个节点？就当前的情况来看，你觉得哪条路径更有「潜力」成为最短路径中的一部分？

从目前的情况来看，显然橙色路径的可能性更大嘛，所以我们希望节点2排在队列靠前的位置，优先被拿出来向后遍历。

所以我们使用PriorityQueue作为队列，让distFromStart的值较小的节点排在前面，这就类似我们之前讲 贪心算法 说到的贪心思路，可以很大程度上优化算法的效率。

总结

经过以上过程的讲解，相信大家对Dijkstra最短路径算法已经有所领悟，复杂的算法往往是由最基础的算法思想一步一步拓展而来，而且一般来说，越是复杂的算法，往往越有套路。