leetcode算法初学------数组篇(二分查找)
二分查找
题目来源:
leetcode:二分查找
题目介绍:
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。
解题思路:
首先注意一点,用二分查找前提有序数组
一切算法源自于数学,从数学领域中不难得出:
对于区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x)
通过不断地把函数f(x)的零点所在的区间一分为二
使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法
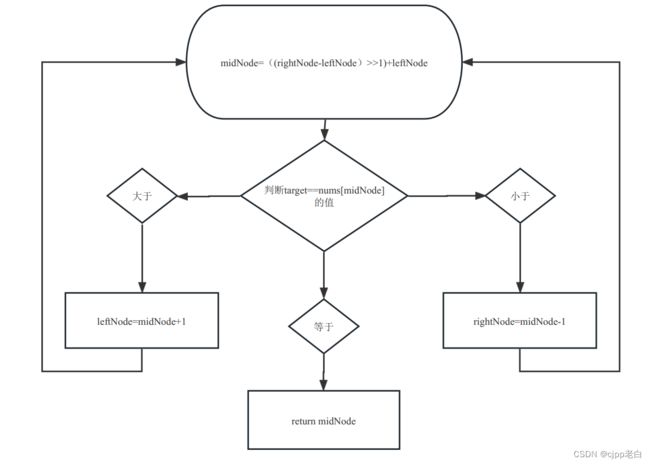 所以我们不难想到[leftNode,rightNode],midNode等于区间的一半。
所以我们不难想到[leftNode,rightNode],midNode等于区间的一半。
让target值与nums[midNode]值进行判断,再根据结果可以分之为两种情况
第一种
target > nums[midNode]; //说明该值在数组靠right那一边
leftNode = midNode + 1; //区间改变left的值
第二种
```c
target < nums[midNode]; //说明该值在数组靠left那一边
rightNode = midNode - 1; //区间改变right的值
我们讨论完区间的范围后,另一个很重要的问题就是循环的语句,也就是人们常常谈论的边界问题。
while(leftNode >= rightNode ) //到底是需要大于还是需要大于等于呢??
大家写二分法经常写乱,主要是因为对区间的定义没有想清楚,区间的定义就是不变量。
要在二分查找的过程中,保持不变量,就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作,这就是循环不变量规则。
写二分法,区间的定义一般为两种,左闭右闭即[leftNode , rightNode ],或者左闭右开即[leftNode , rightNode )。
接下来代码实现分析一下两者区别
public class Search {
public static void main(String[] args) {
int[] nums = {-1, 0, 3, 5, 9, 12};
System.out.println(search(nums, 12));
}
public static int search(int[] nums, int target) {
// 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算
if (target < nums[0] || target > nums[nums.length - 1]) {
return -1;
}
int leftNode = 0;//左边下标
int rightNode = nums.length - 1;//右边下标
while (leftNode <= rightNode) { //或者用 while(leftNode < rightNode)因为left == right的时候,在[leftNode, rightNode)是无效的空间,所以使用 <
int midNdoe = ((rightNode - leftNode) >> 1) + leftNode;// 等同于(left + right)/2 -->防止溢出
if (target == nums[midNdoe]) {
return midNdoe;
} else if (target > nums[midNdoe]) {
leftNode = midNdoe + 1;//把左边下标移动 缩小空间
} else {
rightNode = midNdoe - 1; //把左边下标移动 缩小空间 若用另一种方法则 rightNode = midNode [target 在左区间,在[left, middle)中]
}
}
return -1;
}
}
总结
二分法的主要关键就是while循环的判断,说白了就是边界问题,区间定义的是不变量,主要遵守循环不变量规则