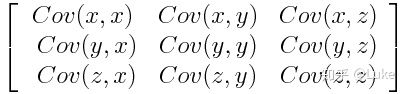pca主成分分析结果解释_主成分分析(PCA)的详细解释

原作者：Zakaria Jaadi
翻译：钟胜杰

这篇文章的目的是提供主成分分析的完整同时比较简化的解释，特别是逐步回答它是如何工作的，这样每个人都可以理解它并利用它，而不必具有很高的数学水平。

PCA实际上是一种使用很广的网络方法，但只有少数人直截了当地解释它是如何工作的，而不会过多地投入技术性的解释。这就是为什么我决定自己发布帖子，用简化的方式呈现它的原因。

在开始解释之前，文章说明了PCA在每个步骤中做了什么，并简化了它背后的数学概念，如标准化，协方差，特征向量和特征值，而没有关注如何计算它们。

所以什么是主成分分析呢？

主成分分析（PCA）是一种降维方法，通常用于通过将数量很多的变量转换为仍包含集合中大部分信息的较少变量来降低数据集的维数。

减少数据集的变量数量自然是以牺牲精度为代价的，但降维是为了简单而略微准确。因为较小的数据集更易于探索和可视化，并且使机器学习算法更容易和更快地分析数据，而无需处理无关的变量。

总而言之，PCA的概念很简单：减少数据集的维数，同时保留尽可能多的信息。

逐步解释PCA

第一步：标准化

此步骤的目的是标准化输入数据集，使数据成比例缩小。

更确切地说，在使用PCA之前必须标准化数据的原因是PCA方法对初始变量的方差非常敏感。也就是说，如果初始变量的范围之间存在较大差异，那么范围较大的变量占的比重较大，和较小的变量相比（例如，范围介于0和100之间的变量较0到1之间的变量会占较大比重），这将导致主成分的偏差。通过将数据转换为同样的比例可以防止这个问题。

在数学上，可以通过减去平均值并除以每个变量的标准偏差来完成。

标准化

标准化完成后，所有变量将转换为相同的范围：[0,1]。

第二步：计算协方差矩阵

此步骤的目的是了解输入数据集的变量相对于彼此平均值变化，换句话说，查看它们是否存在关系。因为有时候，变量由于高度相关，这样就会包含冗余信息。因此，为了识别变量的相关性，我们计算协方差矩阵。

协方差矩阵是p×p对称矩阵（其中p是维数），变量与变量之间的协方差作为矩阵元素。例如，对于具有3个变量x，y和z的三维数据集，协方差矩阵是以下的3×3矩阵：

3维的协方差矩阵

由于变量自身的协方差是方差（

​），因此在主对角线（左上角到右下角）中，我们实际上具有每个起始变量的方差。并且由于协方差是可交换的（

），协方差矩阵相对于主对角线是对称的，这意味着上三角形部分和下三角形部分是相等的。

协方差矩阵变量有什么用呢？

实际上协方差的符号起作用：

• 如果是正的话：两个变量一起增加或减少（相关），
• 如果是负的话：当一个变量增加时，另一个变量减少（不相关）

现在，我们知道协方差矩阵不仅仅是一个矩阵，而是展示变量相关性的矩阵，让我们进入下一步。

第三步：计算协方差矩阵的特征向量和特征值以识别主成分

特征向量和特征值是我们需要从协方差矩阵计算的线性代数概念，以便确定数据的主要成分。 在开始解释这些概念之前，让我们首先理解主成分的含义。

主成分是新变量，是初始变量的线性组合。这些组合以新变量（即主成分）不相关的方式完成，并且初始变量内的大部分信息被压缩或压缩到第一组分中。比如，10维数据提供10个主要组件，但PCA尝试在第一个组件中获取最大可能信息，然后在第二个组件中获得最大剩余信息，依此类推。

如果你有一个10维数据，你最终会得到类似下面的图中显示的内容，其中第一个主要组件包含原始数据集的大部分信息，而最后一个只携带少数几个。因此，以这种方式组织信息，可以在不丢失太多信息的情况下减少维度，并通过丢弃携带较少信息的组件来实现这一点。

每个主成分方差所占的比重

主成分不是很好解释，并且对我们没有任何实际意义，因为它们被构造为初始成分的线性组合。 从几何学上讲，主成分表示解释最大方差量的数据的方向，也就是说，捕获数据的大部分信息的线。这里方差和信息之间的关系是，线所承载的方差越大，数据点沿着它的分散越大，沿着线的色散越大，它所具有的信息就越多。简单地说，只需将主成分视为新轴，然后从这个轴查看和评估数据。

PCA怎么构建主成分？

由于数据中存在与变量一样多的主成分，因此主成分以第一主成分占数据集中最大可能方差的方式构造。例如，假设我们的数据集的散点图如下所示，我们可以猜出第一个主成分吗？它大致是与紫色标记匹配的线，因为它穿过原点，并且它是点（红点）的投影最分散的线。或者从数学上讲，它是最大化方差的线（从投影点（红点）到原点的平方距离的平均值）。

第二主成分以相同的方式计算，条件是它与第一主成分不相关（即垂直），并且它占下一个最高方差。这一直持续到计算出总共p个主成分，等于原始变量数。 现在我们理解了主成分的含义，让我们回到特征向量和特征值。你首先需要知道的是它们总是成对出现，因此每个特征向量都有一个特征值。它们的数量等于数据的维数。例如，对于三维数据集，存在3个变量，因此存在3个具有3个对应特征值的特征向量。 协方差矩阵的特征向量实际上是方差最多的轴的方向（大多数信息），我们称之为主成分。并且特征值只是附加到特征向量的系数，它们给出了每个主成分中携带的方差量。 通过按特征值的顺序对特征向量进行排序，从最高到最低，按重要性顺序得到主要成分。

例子：

假设我们的数据集是2维的，有2个变量，​，并且协方差矩阵的特征向量和特征值如下：

如果我们按降序对特征值进行排序，则得到

​，这意味着对应于第一主成分（PC1）的特征向量是​

，而对应于第二成分（PC2）的特征向量是

​。

在具有主成分之后，为了计算每个成分所占的方差（信息）的百分比，我们将每个成分的特征值除以特征值的总和。如果我们在上面的例子中应用它，我们发现PC1和PC2分别携带96％和4％的数据方差。

第四步：特征向量

正如我们在上一步中所看到的，计算特征向量并按其特征值按降序排序，使我们能够按重要性顺序找到主成分。在这个步骤中，我们要做的是，选择是保留所有这些组件还是丢弃那些重要性较低的组件（低特征值），并与其余组件形成一个我们称之为特征向量的向量矩阵。 因此，特征向量只是一个矩阵，其中包含我们决定保留的组件的特征向量作为列。这使其成为降维的第一步，因为如果我们选择仅保留​

个特征向量中的​

个，则最终数据集将只有

维。

例子：

继续前一步骤的示例，我们可以形成具有特征向量​和​的特征向量：

或者丢弃特征向量​，这是较不重要的特征向量​，这就剩下​形成的特征向量：

丢弃特征向量v2将使维数减少1，并且因此将导致最终数据集中的信息丢失。但鉴于v2仅携带4％的信息，因此损失并不重要，我们仍将拥有v1所载信息的96％。

因此，正如我们在示例中看到的那样，您可以选择是保留所有组件还是丢弃不重要的组件，具体取决于您要查找的内容。

最后一步：沿主要组件轴重新绘制数据

在前面的步骤中，除了标准化之外，您不对数据进行任何更改，只需选择主要组件并形成特征向量，但输入数据集始终保持原始轴的方式（即初始变量）。

在这个最后一步中，目标是使用由协方差矩阵的特征向量形成的特征向量，将数据从原始轴重新定向到由主成分表示的数据（因此称为主成分分析）。这可以通过将原始数据集的转置乘以特征向量的转置来完成。

参考：

• [Steven M. Holland, Univ. of Georgia]: Principal Components Analysis
• [skymind.ai]: Eigenvectors, Eigenvalues, PCA, Covariance and Entropy
• [Lindsay I. Smith] : A tutorial on Principal Component Analysis

原文链接: A step by step explanation of Principal Component Analysis