恋上数据结构与算法第三季二叉树

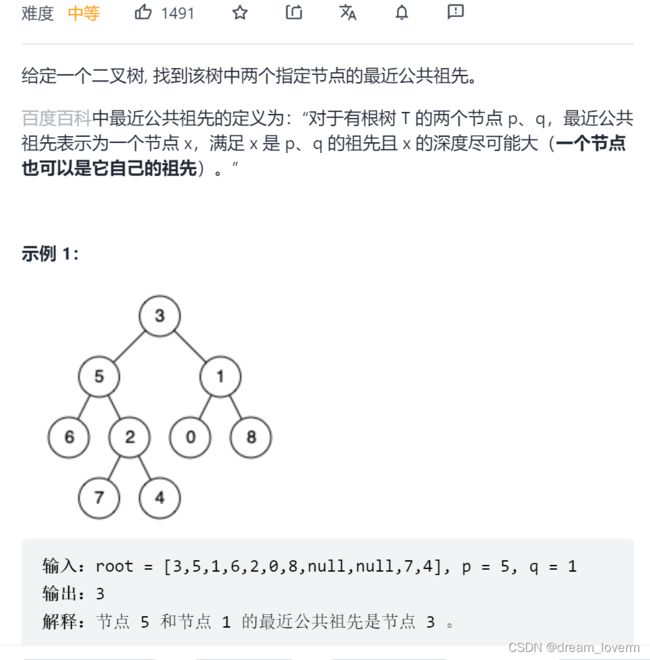
1._236_二叉树的最近公共祖先

标签：树、二叉树

思路：去以root为根节点的二叉树中查找p、q的最近公共祖先

1）如果p、q同时存在与这棵二叉树中、成功返回它们的最近公共祖先

2）如果p、q都不存在于这棵二叉树中，返回Null;

3)  如果只有p存在于这棵二叉树中，返回p

4）如果只有q存在于这棵二叉树中，返回q

对root的左右子树分别寻找最近公共祖先，结果有以下四种情况：

//        1.left != null right != null  return root p、q一个在左子树，一个在右子树中
//        2.left != null right == null  return left p、q都在左子树
//        3.left == null right != null  return right p、q都在右子树
//        4.left == null right == null  return right  左右子树都找不到p、q

代码：

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {

        if(root == null || root == p || root == q) return root;
        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);
//        1.left != null right != null  return root
//        2.left != null right == null  return left
//        3.left == null right != null  return right
//        4.left == null right == null return right
        if(left != null && right != null) return root;
        return (left != null) ? left : right;

    }

2._99_恢复二叉搜索树

 

标签：树、二叉树、二叉搜索树

思路1：二叉搜索树的特点是中序遍历的结果是升序的，对二叉搜索树进行中序遍历，找出逆序对。有两种情况：

1）将原本挨在一起的节点交换，将会产生唯一的一个逆序对；

2）将原本并非挨在一起的节点交换，会产生两个逆序对；

找出逆序对的头节点和尾节点，对两个节点的值进行交换。

找逆序对：判断节点的值和它前驱节点(prev)的值的大小。

代码：

   public void recoverTree(TreeNode root){
        findWrongNodes(root);
        int tmp = first.val;
        first.val = second.val;
        second.val = tmp;
    }

    private void findWrongNodes(TreeNode root) {
        if(root == null) return;
        findWrongNodes(root.left);
        //出现了逆序对
        if(prev != null && prev.val > root.val){
            second = root;
            if(first != null) return;
            first = prev;
        }
        prev = root;
        findWrongNodes(root.right);

    }

时间复杂度：O(n) 空间复杂度：O(h)

思路2：二叉树的Morris遍历（线索二叉树）

执行步骤：

 代码：

    public void recoverTreeByMorris(TreeNode root){
        TreeNode node = root;
        while (node != null) {
            if (node.left != null) {
//                找到前驱节点
                TreeNode pred = node.left;
                //找前驱节点
                while (pred.right != null && pred.right != node) {
                    pred = pred.right;
                }
                if (pred.right == null) {
                    pred.right = node;
                    node = node.left;
                } else {
                    find(node);
                    pred.right = null;
                    node = node.right;
                }
            } else {
                find(node);
                node = node.right;
            }
        }
        int tmp = first.val;
        first.val = second.val;
        second.val = tmp;

    }
    private void find(TreeNode root){
        //出现了逆序对
        if(prev != null && prev.val > root.val){
            second = root;
            if(first != null) return;
            first = prev;
        }
        prev = root;
    }

时间复杂度：O(n)  空间复杂度：O(1)

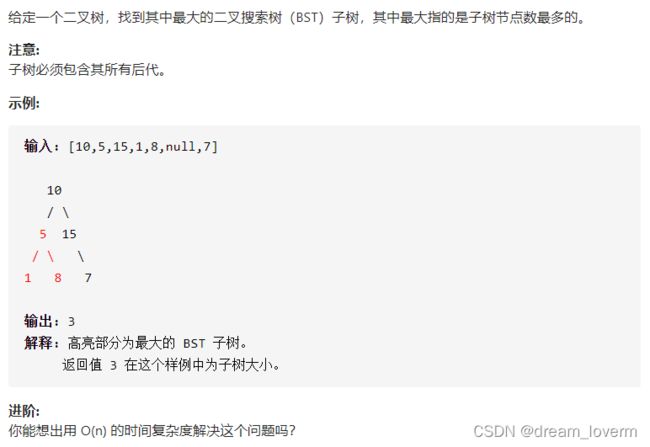
3._333_最大BST子树

标签：树

思想：

1）自顶向下

代码：

    public int largestBSTSubtree(TreeNode root) {
        if(root == null )return 0;
        if(isBST(root)) return NodeCount(root);
        int L = largestBSTSubtree(root.left);
        int R = largestBSTSubtree(root.right);
        return Math.max(L,R);

    }
    private boolean isBST(TreeNode root){
        return isBST(root,Integer.MIN_VALUE,Integer.MAX_VALUE);
    }
    private int NodeCount(TreeNode node){

        if(node == null) return 0;
        return 1 + NodeCount(node.left) + NodeCount(node.right);
    }

    private boolean isBST(TreeNode root,int min,int max){
        if(root == null) return true;
        return min < root.val && root.val < max && isBST(root.left,min,root.val) && isBST(root.right,root.val,max);
    }

 2）自底向上

思路：建一个类存储最大BST子树的信息，包括节点数量、根节点、最大值和最小值

          getInfo()用来返回以root为根节点的二叉树的最大BST子树的信息

代码：

public int largestBSTSubtree(TreeNode root) {
        if(root == null) return 0;
        return getInfo(root).size;
    }

    private Info getInfo(TreeNode root) {
        if (root == null) return null;
        Info li = getInfo(root.left);
        Info ri = getInfo(root.right);
        /**
         * 有4中情况，以root为根节点的二叉树就是一棵BST，即最大BST就是其本身
         * ① li != null && ri != null
         *   && li.root == root.left && root.val > li.max
         *   && ri.root == root.right && root.val < ri.min;
         * ② li != null && ri == null
         *   && li.root == root.left && root.val > li.max
         * ③ li == null && ri != null
         *   && ri.root == root.right && root.val < ri.min
         * ④ li == null && ri == null
         */
        int leftSize = -1, rightSize = -1, max = root.val, min = root.val;
        if (li == null) {
            leftSize = 0;

        } else if (li.root == root.left && root.val > li.max) {
            leftSize = li.size;
            min = li.min;
        }
        if (ri == null) {
            rightSize = 0;

        } else if (ri.root == root.right && root.val < ri.min) {
            rightSize = ri.size;
            max = ri.max;
        }
//        if(（以上两个if各要有一个成立，以root为根节点的二叉树就是BST){
//            return new Info(root,1+li.size+ri.size,li.min,ri.max);
//        }
        if (leftSize >= 0 && rightSize >= 0) {
            return new Info(1 + leftSize + rightSize, root, max, min);

        }
        if(li != null && ri != null) return (li.size > ri.size) ? li : ri;

        return (li != null) ? li : ri;
    }
private static class Info{
    public int size;
    public TreeNode root;
    public int max;
    public int min;

    public Info(int size, TreeNode root, int max, int min) {
        this.size = size;
        this.root = root;
        this.max = max;
        this.min = min;
    }
}