Matlab数据统计与分析（三）——常见分布随机数的产生及统计作图
本文将介绍常见分布的随机数如何产生以及一些简单的统计作图。
一、常见分布的随机数的产生
随机数是专门的随机试验的结果。在统计学的不同技术中需要使用随机数，比如在从统计总体中抽取有代表性的样本的时候。而matlab直接提供了产生随机数的通用函数，但针对不同的分布，函数形式会有所不同，但通用公式如下：
命令：namernd(A,B,m,n)
y = random(‘name’,A1,A2,A3, m, n)
说明：对于namernd(A,B,m,n)函数，m和n表示产生随机数的矩阵大小，例如m=1，n=1就表示产生一个随机数；m=2，n=2就表示产生一个2*2的随机数矩阵，name表示函数名。
下面表格列出了各种分布的随机数生成函数
| 函数名 | 调用形式 | 注 释 |
|---|---|---|
| betarnd | betarnd(A, B,m,n) | 参数为A, B的β分布随机数 |
| binornd | binornd(N,P,m,n) | 参数为N, p的二项分布随机数 |
| chi2rnd | chi2rnd(N, m, n) | 自由度为N的χ 2 分布随机数 |
| exprnd | exprnd(Lambda,m,n) | 参数为Lambda的指数分布随机数 |
| frnd | frnd(N1, N2, m,n) | 第一自由度为N1,第二自由度为N2的F分布随机数 |
| gamrnd | gamrnd(A, B, m,n) | 参数为A, B的γ分布随机数 |
| geornd | geornd(P,m,n) | 参数为 P的几何分布随机数 |
| hygernd | hygernd(M,K,N,m,n) | 参数为 M，K，N的超几何分布随机数 |
| lognrnd | lognrnd(MU, SIGMA, m, n) | 参数为MU, SIGMA的对数正态分布随机数 |
| nbinrnd | nbinrnd(R, P,m,n) | 参数为R, P的负二项式分布随机数 |
| ncfrnd | ncfrnd(N1, N2, delta,m,n) | 参数为N1,N2, delta的非中心F分布随机数 |
| nctrnd | nctrnd(N, delta, m,n) | 参数为N, delta的非中心t分布随机数 |
| ncx2rnd | ncx2rnd(N, delta, m,n) | 参数为N, delta的非中心卡方分布随机数 |
| normrnd | normrnd(MU, SIGMA, m,n) | 参数为MU, SIGMA的正态分布随机数 |
| poissrnd | poissrnd(Lambda,m,n) | 参数为Lambda的泊松分布随机数 |
| raylrnd | raylrnd(B, m,n) | 参数为B的瑞利分布随机数 |
| trnd | trnd(N, m,n) | 自由度为N的t分布随机数 |
| unidrnd | unidrnd(N,m, n) | 离散型均匀分布随机数 |
| unifrnd | unifrnd ( A,B,m,n) | (A,B)上连续型均匀分布随机数 |
| weibrnd | weibrnd(A, B,m, n) | 参数为A, B的威布尔分布随机数 |
例：用两种命令产生符合正态分布N[10，0.5]的2 行 3 列个随机数.
>> n=normrnd(10, 0.5, 2, 3)
n =
10.2688 8.8706 10.1594
10.9169 10.4311 9.3462
>> y=random('norm', 10, 0.5, 2, 3)
y =
9.7832 11.7892 9.3251
10.1713 11.3847 11.5175
二、直方图与经验累积分布函数图形
1.在统计学中，我们往往要求根据实验数据, 绘出直方图, 来显示数据的分布特征, 进而观察实验数据所反映的统计规律。因此在本小节中我们将学习一些简单的统计直方图的绘制方法以及经验累积分布函数图形的绘制。
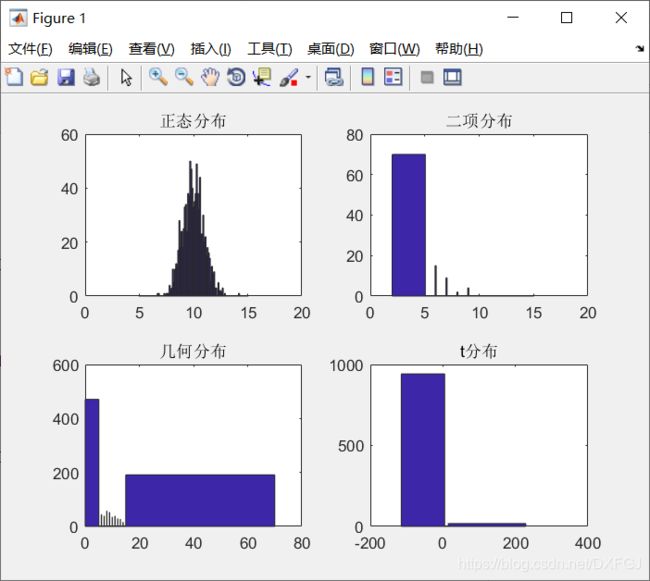
直方图的绘制函数为hist函数，在绘图部分有所讲述，本部分主要借助产生的常见分布的随机数去观察几种分布函数的直方图。
x=5:0.1:15;
y1=normrnd(10, 1,1,1000) ;
subplot(2,2,1)
hist(y1, x) ;
title('正态分布')
y2 = binornd(10,0.5,1,100);
subplot(2,2,2);
hist(y2, x) ;
title('二项分布')
y3 = geornd(0.1,1,1000);
subplot(2,2,3);
hist(y3, x) ;
title('几何分布')
y4 = trnd(1,1,1000);
subplot(2,2,4);
hist(y4, x) ;
title('t分布')
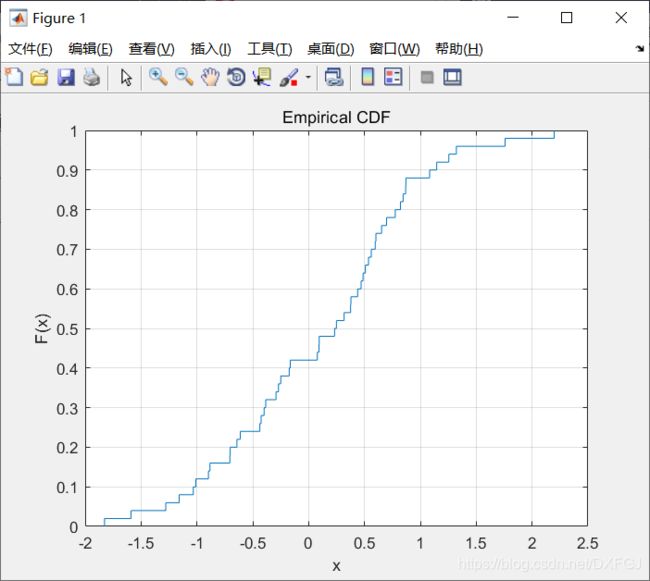
2.在第二讲中讲过计算随机变量的累积概率值的函数，本节则要讲述如何去绘制某一分布的经验累积分布函数图形，将会用到的函数是cdfplot函数，下面就一起来看看它的用法吧。
cdfplot(X) % 作样本 X(向量)的累积分布函数图形.
h = cdfplot(X) %h表示曲线的句柄.
[h,stats] = cdfplot(X) %stats 表示样本的一些特征:样本最小值、最大值、平均值、中位数和标准差.
具体通过以下代码来展示说明：
例：产生 50 个标准正态分布的随机数, 指出它们的分布特征, 并画出经验累计分布函数图。
>> X=normrnd (0,1,50,1);
[h,stats]=cdfplot(X)
h =
Line - 属性:
Color: [0 0.4470 0.7410]
LineStyle: '-'
LineWidth: 0.5000
Marker: 'none'
MarkerSize: 6
MarkerFaceColor: 'none'
XData: [1×102 double]
YData: [1×102 double]
ZData: [1×0 double]
显示 所有属性
stats =
包含以下字段的 struct:
min: -1.8269
max: 2.1978
mean: 0.1036
median: 0.2412
std: 0.8524
从图中可以看出，随着x的不断增大，累计概率密度的值越来越接近1，这符合正态分布的特点。