第十三届蓝桥杯大赛省赛Python-A组真题

一、 裁纸刀

1、题目

小蓝有一个裁纸刀，每次可以将一张纸沿一条直线裁成两半。
小蓝用一张纸打印出两行三列共 6 个二维码，至少使用九次裁出来，下图给出了一种裁法。

在上面的例子中，小蓝的打印机没办法打印到边缘，所以边缘至少要裁4次。另外，小蓝每次只能裁一张纸，不能重叠或者拼起来裁。
如果小蓝要用一张纸打印出 20 行 22 列共 440 个二维码，他至少需要裁多少次？

2、解析

3、Python代码

代码

运行结果

二、寻找整数

1、题目

有一个不超过$10^{17}$的正整数 n，知道这个数除以 2 至 49 后的余数如下表所示，求这个正整数最小是多少。

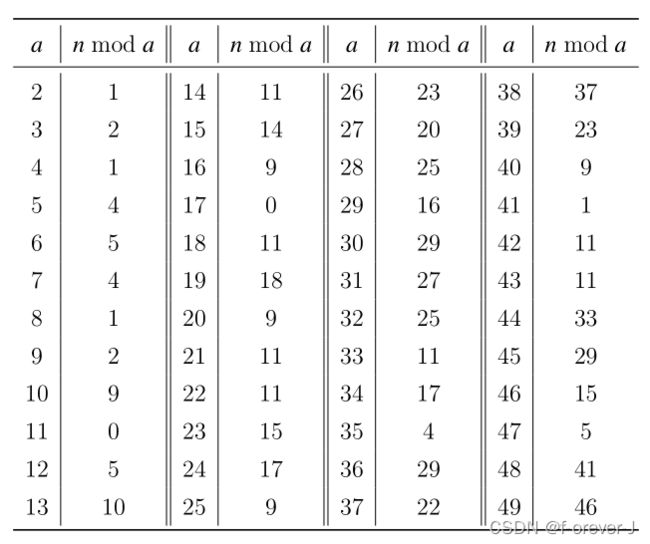
2、解析

3、Python代码

代码

运行结果

三、质因数个数

1、题目

给定正整数 n，请问有多少个质数是 n 的约数。

输入
输入的第一行包含一个整数 n。

输出
输出一个整数，表示 n 的质数约数个数。

2、样例

输入

396

输出

3

【样例说明】
396 有 2, 3, 11 三个质数约数。

3、解析

4、Python代码

代码

运行结果

四、矩形拼接

1、题目

已知 3 个矩形的大小依次是$a_1$×$b_1$ ,$a_2$×$b_2$ 和$a_3$×$b_3$ 。用这 3 个矩形能拼出的所有多边形中，边数最少可以是多少？
例如用 3×2 的矩形（用 A 表示）、4×1 的矩形（用 B 表示）和 2×4 的矩形（用 C 表示）可以拼出如下 4 边形。

例如用 3×2 的矩形（用 A 表示）、3×1 的矩形（用 B 表示）和 1×1 的矩形（用 C 表示）可以拼出如下 6 边形。

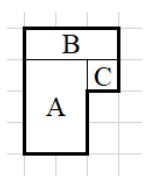
输入
输入包含多组数据。
第一行包含一个整数 T，代表数据组数。
以下 T 行，每行包含 6 个整数$a_1$，$b_1$，$a_2$ ，$b_2$，$a_3$，$b_3$，其中$a_1$，$b_1$是第一个矩形的边长，$a_2$，$b_2$是第二个矩形的边长，$a_3$，$b_3$是第三个矩形的边长。

输出
对于每组数据，输出一个整数代表答案。

2、样例

输入

2
2 3 4 1 2 4
1 2 3 4 5 6

输出

4
8

3、解析

4、Python代码

代码

运行结果

五、消除游戏

1、题目

在一个字符串 S 中，如果$S_i$ =$S_{i-1}$且 $S_i$ ≠$S_{i+1}$，则称$S_i$和$S_{i+1}$为边缘字符。如果 $S_i$ ≠$S_{i-1}$且 $S_i$ =$S_{i+1}$，则$S_{i-1}$和$S_i$也称为边缘字符。其它的字符都不是边缘字符。
对于一个给定的串 S，一次操作可以一次性删除该串中的所有边缘字符（操作后可能产生新的边缘字符）。
请问经过$2^{64}$次操作后，字符串 S 变成了怎样的字符串，如果结果为空则输出 EMPTY。

输入
输入一行包含一个字符串 S 。

输出
输出一行包含一个字符串表示答案，如果结果为空则输出 EMPTY。

2、样例

输入1

edda

输出1

EMPTY

输入2

sdfhhhhcvhhxcxnnnnshh

输出2

s

3、解析

4、Python代码

代码

运行结果

六、重新排序

1、题目

给定一个数组 A 和一些查询$L_i$，$R_i$ ，求数组中第$L_i$至第$R_i$ 个元素之和。
小蓝觉得这个问题很无聊，于是他想重新排列一下数组，使得最终每个查询结果的和尽可能地大。小蓝想知道相比原数组，所有查询结果的总和最多可以增加多少?

输入
输入第一行包含一个整数 n。
第二行包含 n 个整数 $A_1$ ,$A_2$ ,··· ,$A_n$，相邻两个整数之间用一个空格分隔。
第三行包含一个整数 m 表示查询的数目。
接下来 m 行，每行包含两个整数$L_i$，$R_i$，相邻两个整数之间用一个空格分隔。

输出
输出一行包含一个整数表示答案。

2、样例

输入

5
1 2 3 4 5
2
1 3
2 5

输出

4

3、解析

4、Python代码

代码

运行结果

七、全排列的价值

1、题目

对于一个排列A=($a_1$,$a_2$,··· ,$a_n$)，定义价值 $c_i$为$a_1$至$a_{i-1}$中小于$a_1$的数的个数，即 $b_i$= |{$a_j$|j < i,$a_j$<$a_i$}|。定义 A 的价值为${\sum }_{i=1}^n{c}_i$。
给定 n，求 1 至 n 的全排列中所有排列的价值之和。

输入
输入一行包含一个整数 n 。

输出
输出一行包含一个整数表示答案，由于所有排列的价值之和可能很大，请输出这个数除以 98244353 的余数。

2、样例

输入

3

输出

9

输入

2022

输出

593300958

【样例说明】
1 至 3 构成的所有排列的价值如下:
(1,2,3) : 0 + 1 + 2 = 3 ；
(1,3,2) : 0 + 1 + 1 = 2 ；
(2,1,3) : 0 + 0 + 2 = 2 ；
(2,3,1) : 0 + 1 + 0 = 1 ；
(3,1,2) : 0 + 0 + 1 = 1 ；
(3,2,1) : 0 + 0 + 0 = 0 ；
故总和为 3 + 2 + 2 + 1 + 1 = 9。

3、解析

4、Python代码

代码

运行结果

八、最长不下降子序列

1、题目

给定一个长度为 N 的整数序列：$A_1$,$A_2$,··· ,$A_n$ 。现在你有一次机会，将其中连续的 K 个数修改成任意一个相同值。请你计算如何修改可以使修改后的数列的最长不下降子序列最长，请输出这个最长的长度。
最长不下降子序列是指序列中的一个子序列，子序列中的每个数不小于在它之前的数。

输入
输入第一行包含两个整数 N 和 K。
第二行包含 N 个整数$A_1$,$A_2$,··· ,$A_n$ 。

输出
输出一行包含一个整数表示答案。

2、样例

输入

5 1
1 4 2 8 5

输出

4

3、解析

4、Python代码

代码

运行结果

九、最优清零方案

1、题目

给定一个长度为 N 的数列$A_1$,$A_2$,··· ,$A_N$ 。现在小蓝想通过若干次操作将这个数列中每个数字清零。
每次操作小蓝可以选择以下两种之一：

1. 选择一个大于 0 的整数，将它减去 1；
2. 选择连续 K 个大于 0 的整数，将它们各减去 1。

小蓝最少经过几次操作可以将整个数列清零？

输入
输入第一行包含两个整数 N 和 K。
第二行包含 N 个整数$A_1$,$A_2$,··· ,$A_N$ 。

输出
输出一个整数表示答案。

2、样例

输入

4 2
1 2 3 4

输出

6

3、解析

4、Python代码

代码

运行结果

十、数的拆分

1、题目

给定 T 个正整数 $a_i$ ，分别问每个$a_i$能否表示为$x_1^{y_1}$· $x_2^{y_2}$的形式，其中$x_1$· $x_2$为正整数，$y_1$· $y_2$为大于等于 2 的正整数。

输入
输入第一行包含一个整数 T 表示询问次数。
接下来 T 行，每行包含一个正整数 $a_i$ 。

输出
对于每次询问, 如果$a_i$能够表示为题目描述的形式则输出 yes，否则输出no 。

2、样例

输入

7
2
6
12
4
8
24
72

输出

no
no
no
yes
yes
no
yes

【样例说明】
第 4,5,7 个数分别可以表示为：
$a_4$ = $2^2$ × $1^2$；
$a_5$ = $2^3$ × $1^2$；
$a_7$ = $2^3$ × $3^2$ 。

3、解析

4、Python代码

代码

运行结果