2023年美国大学生数学建模MCM问题Y:了解二手帆船的价格-解题思路及代码分享
2023 MCM
Problem Y: Understanding Used Sailboat Prices
2023年MCM问题Y:了解二手帆船的价格
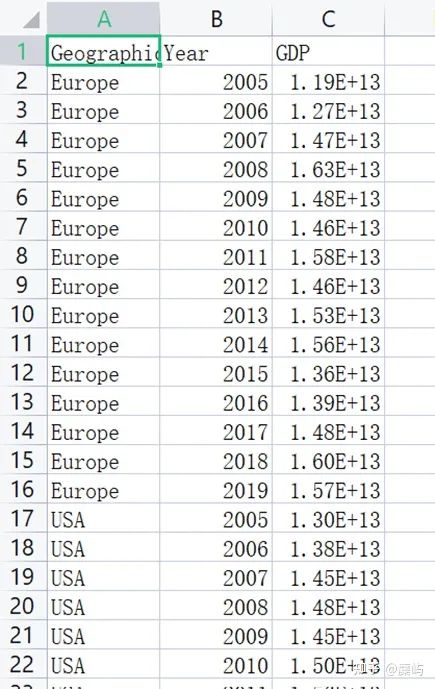
和许多奢侈品一样,帆船的价值会随着老化和市场条件的变化而变化。附件中所附的“2023_MCM_Problem_Y_Boats.xlsx”文件包括了2020年12月在欧洲、加勒比海和美国登广告出售的大约3500艘36至56英尺长的帆船的数据。
一、题目评价
典型的数据分析题目,考察预测模型,有现成数据,题目里多次提示可以自行增添相关数据,建议补充一些数据来辅助建模与分析。相对来说,本题难度不大,适合新手小白快速上手。
二、解题思路
1.数据清洗
1. 数据读取与观察:
由于原始excel编码为ansi,直接使用python读取会报错,需要用记事本打开转换编码格式为utf-8,转存为csv格式,再使用python的pandas包读取。
缺失值查看:
import pandas as pd
df1=pd.read_csv('Monohulled Sailboats.csv')
df2=pd.read_csv('Catamarans.csv')
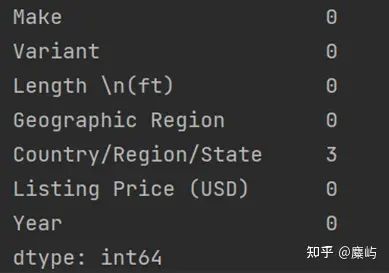
print(df1.isnull().sum())
print(df2.isnull().sum())输出结果:
1
2
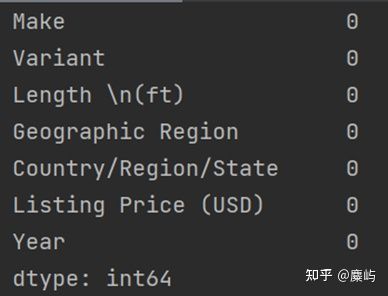
由此可见,sheet1“Monohulled Sailboats”中有3个缺失值,而sheet2“Catamarans”中无缺失值。通过excel的筛选,可以快速定位到缺失值:
| Make | Variant | Length (ft) |
Geographic Region | Country/Region/State | Listing Price (USD) | Year |
| Beneteau | Oceanis 54 | 54 | USA | $479,805 | 2013 | |
| Delphia | 46 cc | 46 | Europe | $314,606 | 2013 | |
| Bavaria | Cruiser 46 | 46 | Europe | $201,640 | 2014 |
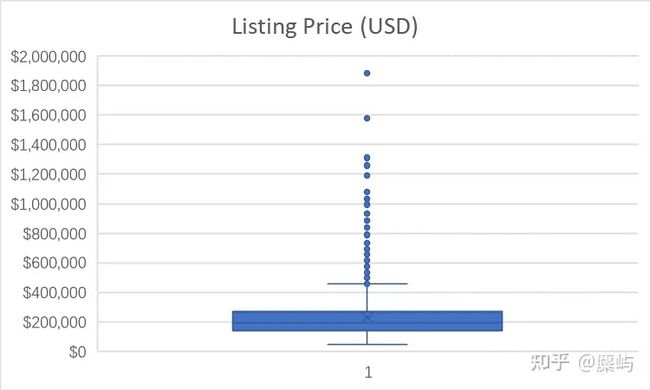
接着我们通过绘制箱线图来查看数据的分布情况:
Monohulled Sailboats
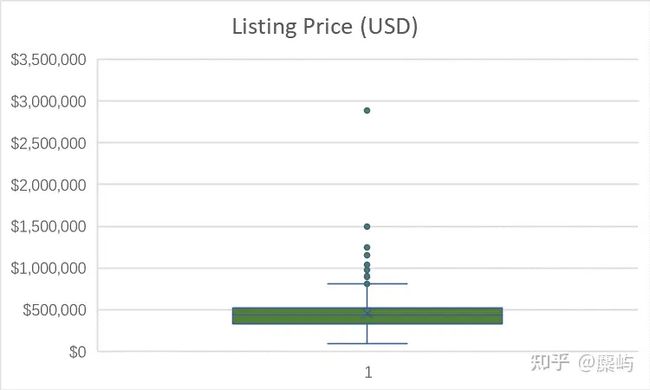
Catamarans
M类船的价格分布在200,000左右,C类船的价格分布在500,000左右
都存在个别偏离总体较明显的异常值,由于数据量本身不大,先标记保留。
数据合并:
我们观察到,两份数据的列名一致,仅仅是船的类型不同,不妨将两份数据合并成一份,便于后边的预测分析操作。
新建一列‘type’,数据为Monohulled Sailboats和Catamarans
#数据合并
df1['type']='Monohulled Sailboats'
df2['type']='Catamarans'
df=pd.concat([df1,df2])数据扩充:
题目给出的数据特征很少,且大部分是离散的分类特征变量,这对于预测问题的帮助比较有限,而题目中提示的很精确(利用其他来源来了解给定帆船的附加特性(如横梁、吃水、位移、索具、帆面积、船体材料、引擎时间、睡眠能力、净空空间、电子设备等)。以及按年份和地区分列的经济数据)
比较好收集的数据便是经济数据
Europe 2518
USA 493
Caribbean 480
数据中主要涉及以上三个地区05-19年的数据,我们可以从《世界银行》World Bank Open Data | Data数据库中找到这些国家历年的经济数据(GDP)。
整理至‘GDP.csv’中
将其合并到df中
df_gdp=pd.read_csv('GDP.csv')
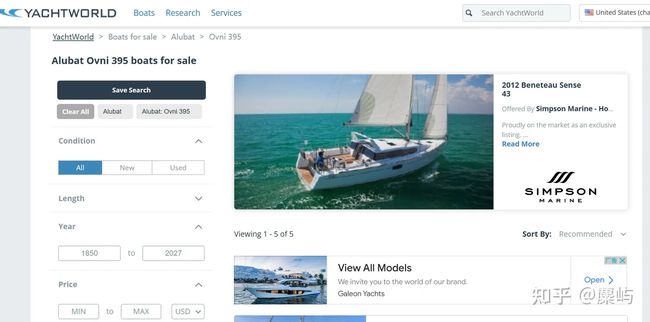
df=pd.merge(df,df_gdp,how='inner',on=['Geographic Region','Year'])其他可能用到的数据Alubat Ovni 395 boats for sale - YachtWorld
2.开发一个数学模型,解释所提供的电子表格中每艘帆船的上市价格。
提到价格预测,不难想到多元线性回归模型。但是考虑到data中只有【船长度】和【价格】以及【年份】三个原始的数值型变量,题目中给出的【生产商】等分类变量难以直接利用。
所以我们应该先针对各细分类别的数据进行可视化分析。
根据之前的箱型图,我们就可以发现,单体帆船的整体价格比双体帆船的价格便宜一些。
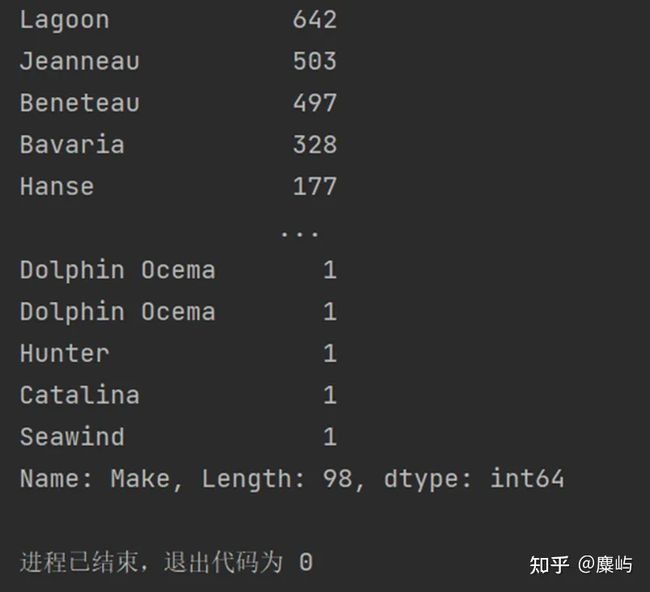
所以我们首先对于【Make】列,即制造商进行分类探讨,首先利用value_counts函数统计出有多少个制造商:
统计结果显示,给出的数据里有98家之多的制造商,且很多制造商只有1-2条数据,这对我们的分类数据观察分析没有帮助,设置阈值lowest_boats_num=20,只统计拥有超过20条船售价数据的生产商,筛选后得到:17家生产商
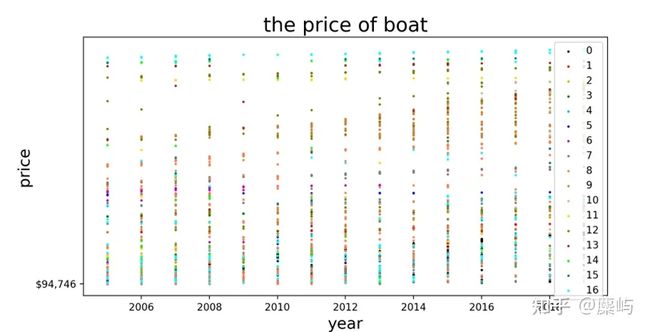
由于类别还是比较多,所以我们继续调大阈值调到100:
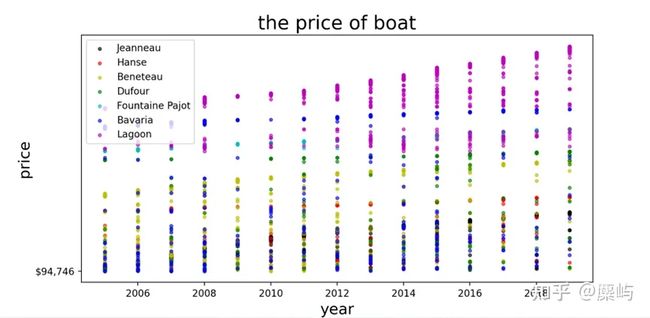
由此我们可以相对比较直观地看出Lagoon制造商生产的船价格偏高,且随着年份,价格持续走高。
参考代码:
#数据可视化
df_maker=df['Make'].value_counts().to_frame()
df_maker=df_maker[df_maker['Make']>100]#设置阈值
lei=list(set(df_maker.index))
print(len(lei))
colors=['k','r','y','g','c','b','m','grey','coral','peru','tan','gold','olive','brown','lime','teal','cyan','blue'
,'navy','plum','pink','indigo','deepskyblue','crimson','hotpink','salmon','darkslategray','aquamarine','b','c']
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 15), dpi=100)
my_y_ticks = np.arange(0, 3000000, 100000)
plt.yticks(my_y_ticks)
for i in range(len(lei)):
data1=df[df['Make']==lei[i]]
plt.scatter(data1['Year'], data1['Listing Price (USD)'], c=colors[i], s=10, alpha=0.6, label=lei[i])
plt.xlabel("year", fontdict={'size': 16})
plt.ylabel("price", fontdict={'size': 16})
plt.title("the price of boat", fontdict={'size': 20})
plt.legend(loc='best')
plt.show()与之同理,我们还可以查看【Variant】【Geographic Region】和【Country/Region/State】对应的价格散点图:
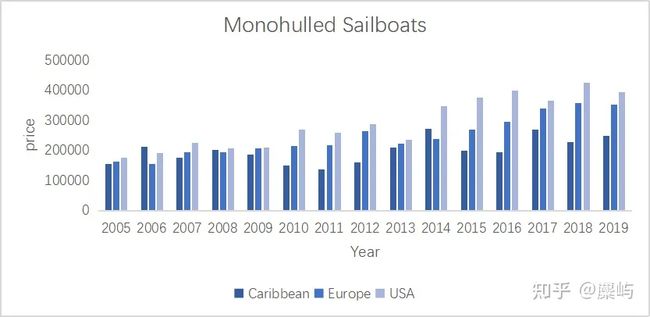
图中显示,欧洲的价格显然偏高。
对应,我们对三个geographic的gdp进行对比分析:
可以看出长远来看,gdp和船价格并没有明显的正相关关系。
为了更好地比较各类的价格,进行聚类的均值计算,在计算前需要把$xxx,xxx类数据转换成float型:
df['Listing Price (USD)']=df['Listing Price (USD)'].apply(lambda x: x[1:])
df['Listing Price (USD)']=df['Listing Price (USD)'].str.replace(',','').astype(float)
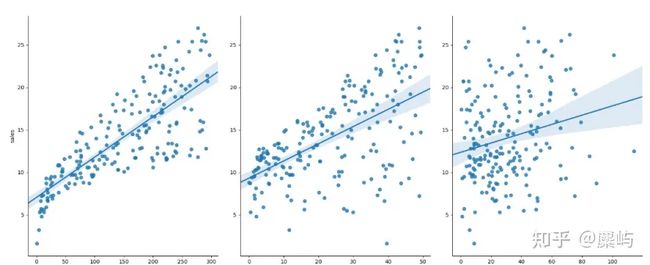
df.groupby(['Year','Geographic Region','type'])['Listing Price (USD)'].mean().to_csv('mean.csv')在探讨完分类特征之后,我们对船长度与价格的关系进行分析:在忽略年份和类型的不同条件下直接计算相关性,发现相关性很弱,接着我们限制年份、类别,发现长度与价格可以看出有正相关性(比较长度越长成本就越高),但是并不是很明显的线性关系。
根据我们上述的分析,发现,单纯地使用多元线性回归预测虽然简单粗暴便于解释,但是并不能利用好给出的类别特征,也难以达到较高的准确度。
但是也不妨先做一下多元线性回归预测的方法,可以在写论文时使用两种方法进行对比:
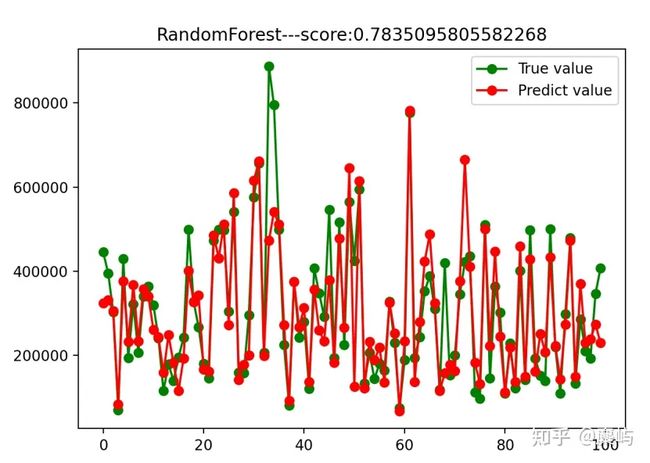
多元线性回归
于是可以采用随机森林的方法进行预测。
变量选取:
【Length (ft)】【Year】【GDP】【Make】【Variant】【Geographic Region】【Country/Region/State】【type】
其中我们需要对字符型变量进行转换:
转换方式为:
(1) 对于类别较少的特征【Geographic Region】和【type】,我们可以直接设为数字0/1/2和0/1,其中geographic的数字0/1/2按顺序依次赋给平均价格由低到高的国家
(2) 对于类别很多的特征【Make】【Variant】和【Country/Region/State】,我们分别统计其类别出现的次数以及平均值:
然后对于具有显著的【贵】或者【便宜】特征的类别进行标记,其他的类记为0.
例如:【Make】中[Privilege, Southerly, Bali, HH Catamarans, Discovery, Nautor, Nautitech, Lagoon]价格偏贵,标记1,而[Beneteau, Dufour, Elan, Bavaria, Dehler, Van De Stadt]价格偏便宜,标记-1,其余标记0
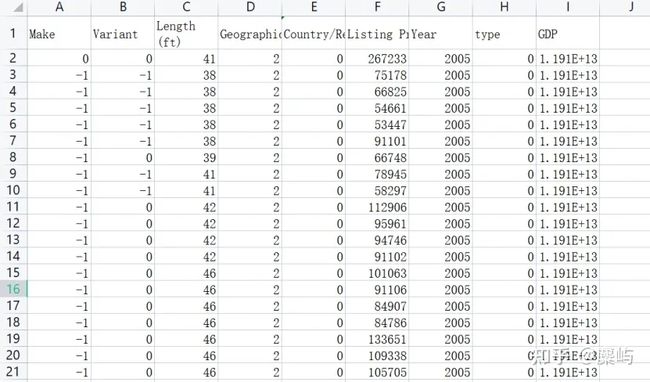
数据处理好后长这样:
接着进行随机森林预测:
至于精度则可以用rmse来衡量。
from sklearn import metrics
y = np.array([1,1])
y_hat = np.array([2,3])
MSE = metrics.mean_squared_error(y, y_hat)
RMSE = metrics.mean_squared_error(y, y_hat)**0.5
MAE = metrics.mean_absolute_error(y, y_hat)
MAPE = metrics.mean_absolute_percentage_error(y, y_hat)2.用你的模型来解释地区对上市价格的影响。讨论是否有任何区域效应在所有的帆船变异中是一致的
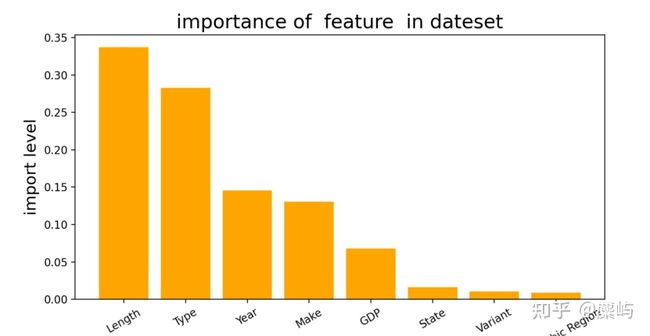
根据我们随机森林得到的结果,探讨各区域特征对预测的影响程度。
除了已有的区域类别、GDP特征难以模拟影响的全面性,因此我们根据数据的可获得性收集以下数据:
【GDP】【货运吞吐量】-世界银行
【船只总量】【船舶市场营收】-《2019全球海运发展评述报告》
这些都是可以代表区域特征的数据。
将这些数据导入随机森林模型,观察预测模型的变化。
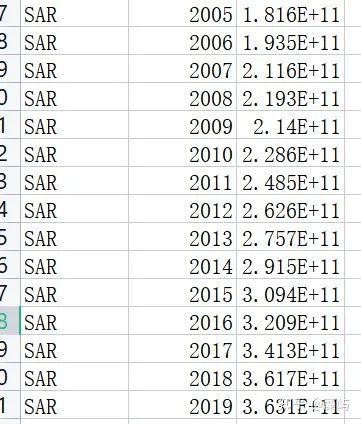
3.您对特定地理区域的建模如何在香港(SAR)市场中有用
根据前面两问,我们知道,GDP、年份、船的类型都跟预测有关系。
如何验证在香港地区的作用则需要找到香港的数据集。
我们只需要将随机森林输出的模型中代入新的GDP年份对应数据即可获得SAR的船预测模型。
然后按照前述方法进行数据转换,生成datafortrain2
代入随机森林模型进行训练,这时我们可以直接删除掉几乎无影响的特征。
4。这对双体船和单壳帆船的效果都是一样的吗?
是不一样的,最开始的分析中可以看出类型的不同,输出的定价模型也不同。所以我们要保留type特征列,为了验证其影响,可以删除type列观察rmse变化情况,或者进行数据分类,对比两类的模型输出结果。