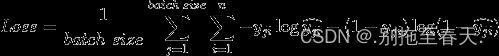【剑指offer】交叉熵损失函数
系列文章目录
梯度消失和梯度爆炸
BN层详解
文章目录
- 系列文章目录
- 什么是交叉熵损失函数
- 详细解释
- 推导过程
- 交叉熵损失函数在单标签分类任务中的使用(二分类任务包含在其中)
- 交叉熵损失函数在多标签分类任务中的使用
- Pytorch 中的 CrossEntropyLoss() 函数
- 参考
什么是交叉熵损失函数
交叉熵损失函数是一种用于衡量模型预测输出与真实标签之间差异的损失函数。它通常用于分类问题中,其中模型输出的是一个概率分布,表示每个类别的可能性。交叉熵损失函数将真实标签的概率分布与模型预测的概率分布进行比较,计算它们之间的交叉熵。交叉熵越小,表示模型的预测结果越接近真实标签,因此优化交叉熵损失函数可以使模型更好地进行分类。
详细解释
在机器学习中,模型的目标通常是最大化似然函数,即让模型的预测概率分布尽可能地接近真实标签的概率分布。交叉熵损失函数正是基于这个思想而来的。
在分类问题中,每个样本都有一个真实的标签,通常用独热编码的形式表示。例如,对于一个三分类问题,第一个样本的真实标签可能是 [ 1 , 0 , 0 ] [1, 0, 0] [1,0,0],表示该样本属于第一类。假设模型预测的概率分布为 [ 0.8 , 0.1 , 0.1 ] [0.8, 0.1, 0.1] [0.8,0.1,0.1],表示模型认为该样本属于第一类的概率为 0.8 0.8 0.8,属于第二类和第三类的概率都为 0.1 0.1 0.1。我们可以看到,模型的预测与真实标签之间存在差异。
交叉熵损失函数的核心思想是,将真实标签的概率分布与模型预测的概率分布进行比较,计算它们之间的交叉熵。它与事件的概率分布密切相关,这也就是为什么神经网络在使用交叉熵损失函数时会先使用函数softmax或者sigmoid函数将网络的输出转换为概率值。如果使用PyTorch设计网络的话,它自带的命令torch.nn.functional.cross_entropy已经将转换概率值的操作整合了进去,所以不需要额外进行转换概率值的操作。交叉熵越小,表示模型的预测结果越接近真实标签,因此优化交叉熵损失函数可以使模型更好地进行分类。具体来说,交叉熵损失函数可以表示为:
L = − 1 n ∑ i = 1 n ∑ j = 1 m y i , j log p i , j L = -\frac{1}{n} \sum_{i=1}^{n} \sum_{j=1}^{m} y_{i,j} \log p_{i,j} L=−n1i=1∑nj=1∑myi,jlogpi,j
其中, n n n 表示样本数, m m m 表示类别数, y i , j y_{i,j} yi,j 表示第 i i i 个样本在第 j j j 个类别上的真实标签, p i , j p_{i,j} pi,j 表示第 i i i 个样本在第 j j j 个类别上的预测概率。可以看到,交叉熵损失函数将真实标签的概率分布与模型预测的概率分布进行比较,计算它们之间的交叉熵。交叉熵的定义如下:
H ( y , p ) = − ∑ j = 1 m y j log p j H(y, p) = -\sum_{j=1}^{m} y_j \log p_j H(y,p)=−j=1∑myjlogpj
其中, y y y 表示真实标签的概率分布, p p p 表示模型预测的概率分布。可以看到,交叉熵的计算方式与熵的计算方式类似,都是将概率分布取对数并进行加权求和。但是,交叉熵的计算方式比熵更加灵活,因为它可以用于比较两个概率分布之间的差异,而熵只能用于衡量一个概率分布的不确定性。
交叉熵损失函数的优化可以使用梯度下降等优化方法进行。在每一次迭代中,计算出模型预测的概率分布与真实标签的概率分布之间的差异,然后根据差异的梯度方向更新模型参数,使得模型的预测结果更加接近真实标签。通过反复迭代,可以逐渐降低交叉熵损失函数的值,使得模型的预测结果更加准确。
推导过程
假设有 n n n 个样本,每个样本有 m m m 个类别,第 i i i 个样本的真实标签为 y i y_i yi,预测的概率分布为 p i p_i pi,则交叉熵损失函数可以表示为:
L = − 1 n ∑ i = 1 n ∑ j = 1 m y i , j log p i , j = − 1 n ∑ i = 1 n ∑ j = 1 m ( 1 − y i , j ) log ( 1 − p i , j ) − y i , j log p i , j \begin{align} L &= -\frac{1}{n} \sum_{i=1}^{n} \sum_{j=1}^{m} y_{i,j} \log p_{i,j} \ &= -\frac{1}{n} \sum_{i=1}^{n} \sum_{j=1}^{m} (1 - y_{i,j}) \log (1 - p_{i,j}) - y_{i,j} \log p_{i,j} \end{align} L=−n1i=1∑nj=1∑myi,jlogpi,j =−n1i=1∑nj=1∑m(1−yi,j)log(1−pi,j)−yi,jlogpi,j
其中, y i , j y_{i,j} yi,j 表示第 i i i 个样本在第 j j j 个类别上的真实标签, p i , j p_{i,j} pi,j 表示第 i i i 个样本在第 j j j 个类别上的预测概率。
上式中的第一个式子可以理解为:对于每个样本,计算其真实标签在预测概率分布中对应的概率,然后取对数并求和,最后再除以样本数 n n n 得到平均交叉熵损失。
第二个式子可以理解为:先将真实标签进行独热编码,然后将其与预测概率分布分别取对数并相乘,最后再取相反数求和得到平均交叉熵损失。
交叉熵损失函数的推导过程比较复杂,但可以通过最大似然估计的思想来理解。假设有一个二分类问题, y y y 表示真实标签, p p p 表示模型预测的概率。则最大似然估计的目标是使得样本的似然概率最大:
L = ∏ i = 1 n p i y i ( 1 − p i ) 1 − y i = ∏ i = 1 n ( 1 − p i ) 1 − y i ∏ i = 1 n p i y i = exp ( − ∑ i = 1 n y i log 1 p i + ( 1 − y i ) log 1 1 − p i ) \begin{align} L &= \prod_{i=1}^{n} p_i^{y_i} (1-p_i)^{1-y_i} \ &= \prod_{i=1}^{n} (1-p_i)^{1-y_i} \prod_{i=1}^{n} p_i^{y_i} \ &= \exp\left(-\sum_{i=1}^{n} y_i \log \frac{1}{p_i} + (1-y_i) \log \frac{1}{1-p_i}\right) \end{align} L=i=1∏npiyi(1−pi)1−yi =i=1∏n(1−pi)1−yii=1∏npiyi =exp(−i=1∑nyilogpi1+(1−yi)log1−pi1)
上式中,第一项表示当 y = 1 y=1 y=1 时,似然概率为 p p p,第二项表示当 y = 0 y=0 y=0 时,似然概率为 1 − p 1-p 1−p。将上式取相反数,即得到二分类问题的交叉熵损失函数:
L = − ∑ i = 1 n y i log p i + ( 1 − y i ) log ( 1 − p i ) L = -\sum_{i=1}^{n} y_i \log p_i + (1-y_i) \log (1-p_i) L=−i=1∑nyilogpi+(1−yi)log(1−pi)
对于多分类问题,可以将其推广到所有类别上,最终得到交叉熵损失函数的公式。
交叉熵损失函数在单标签分类任务中的使用(二分类任务包含在其中)
单标签任务,顾名思义,每个样本只能有一个标签,比如ImageNet图像分类任务,或者MNIST手写数字识别数据集,每张图片只能有一个固定的标签。
对单个样本,假设真实分布为y,网络输出分布为 y ^ \widehat{y} y ,总的类别数为n,则在这种情况下,交叉熵损失函数的计算方法为:
L o s s = − ∑ i = 1 n y i log y ^ i Loss =-\sum_{i=1}^n y_i \log \widehat{y}_i Loss=−i=1∑nyilogy i
用一个例子来说明,在手写数字识别任务中,如果样本是数字“5”,那么真实分布应该为:[ 0, 0, 0, 0, 0, 1, 0, 0, 0, 0 ],
如果网络输出的分布为:[ 0.1, 0.1, 0, 0, 0, 0.7, 0, 0.1, 0, 0 ],则应为10,那么计算损失函数得:
Loss = − 0 × log 0.1 − 0 × log 0.1 − 0 × log 0 − 0 × log 0 − 0 × log 0 − 1 × log 0.7 − 0 × log 0 − 0 × log 0.1 − 0 × log 0 − 0 × log 0 ≈ 0.3567 \begin{aligned} & \text { Loss }=-0 \times \log 0.1-0 \times \log 0.1-0 \times \log 0-0 \times \log 0-0 \times \log 0-1 \times \\ & \log 0.7-0 \times \log 0-0 \times \log 0.1-0 \times \log 0-0 \times \log 0 \approx 0.3567\end{aligned} Loss =−0×log0.1−0×log0.1−0×log0−0×log0−0×log0−1×log0.7−0×log0−0×log0.1−0×log0−0×log0≈0.3567
如果网络输出的分布为:[ 0.2, 0.3, 0.1, 0, 0, 0.3, 0.1, 0, 0, 0 ],那么计算损失函数得:
Loss = − 0 × log 0.2 − 0 × log 0.3 − 0 × log 0.1 − 0 × log 0 − 0 × log 0 − 1 × log 0.3 − 0 × log 0.1 − 0 × log 0 − 0 × log 0 − 0 × log 0 ≈ 1.2040 \begin{aligned} & \text { Loss }=-0 \times \log 0.2-0 \times \log 0.3-0 \times \log 0.1-0 \times \log 0-0 \times \log 0- \\ & 1 \times \log 0.3-0 \times \log 0.1-0 \times \log 0-0 \times \log 0-0 \times \log 0 \approx 1.2040\end{aligned} Loss =−0×log0.2−0×log0.3−0×log0.1−0×log0−0×log0−1×log0.3−0×log0.1−0×log0−0×log0−0×log0≈1.2040
上述两种情况对比,第一个分布的损失明显低于第二个分布的损失,说明第一个分布更接近于真实分布,事实也确实是这样。
对一个batch,单标签n分类任务的交叉熵损失函数的计算方法为:
交叉熵损失函数在多标签分类任务中的使用
多标签分类任务,即一个样本可以有多个标签,比如一张图片中同时含有“猫”和“狗”,这张图片就同时拥有属于“猫”和“狗”的两种标签。在这种情况下,我们将sigmoid函数作为网络最后一层的输出,把网络最后一层的每个神经元都看做任务中的一个类别,以图像识别任务为例,网络最后一层的输出应该理解为:网络认为图片中含有这一类别物体的概率。而每一类的真实标签都只有两种可能值,即“图片中含有这一类物体”和“图片中不含有这一类物体”,这是一个二项分布。综上所述,对多分类任务中的每一类单独分析的话,真实分布是一个二项分布,可能的取值为0或者1,而网络预测的分布可以理解为标签是1的概率。此外,由于多标签分类任务中,每一类是相互独立的,所以网络最后一层神经元输出的概率值之和并不等于1。对多标签分类任务中的一类任务来看,交叉熵损失函数为:
![]()
总的交叉熵为多标签分类任务中每一类的交叉熵之和。
对一个batch,多标签n分类任务的交叉熵损失函数的计算方法为:
Pytorch 中的 CrossEntropyLoss() 函数
Pytorch中计算的交叉熵是采用交叉熵的另外一种方式计算得到的:

Pytorch中CrossEntropyLoss()函数的主要是将softmax-log-NLLLoss合并到一块得到的结果。
- Softmax后的数值都在0~1之间,所以 ln 之后值域是负无穷到0。
- 然后将Softmax之后的结果取log,将乘法改成加法减少计算量,同时保障函数的单调性 。 NLLLoss 的结果就是把上面的输出与
- Label 对应的那个值拿出来,去掉负号,再求均值。
import torch
import torch.nn as nn
x_input = torch.randn(3, 3) # 随机生成输入
print('x_input:\n', x_input)
y_target = torch.tensor([1, 2, 0]) # 设置输出具体值 print('y_target\n',y_target)
# 计算输入softmax,此时可以看到每一行加到一起结果都是1
softmax_func = nn.Softmax(dim=1)
soft_output = softmax_func(x_input)
print('soft_output:\n', soft_output)
# 在softmax的基础上取log
log_output = torch.log(soft_output)
print('log_output:\n', log_output)
# 对比softmax与log的结合与nn.LogSoftmaxloss(负对数似然损失)的输出结果,发现两者是一致的。
logsoftmax_func=nn.LogSoftmax(dim=1)
logsoftmax_output=logsoftmax_func(x_input)
print('logsoftmax_output:\n', logsoftmax_output)
# pytorch中关于NLLLoss的默认参数配置为:reducetion=True、size_average=True
nllloss_func = nn.NLLLoss()
nlloss_output = nllloss_func(logsoftmax_output, y_target)
print('nlloss_output:\n', nlloss_output)
# 直接使用pytorch中的loss_func=nn.CrossEntropyLoss()看与经过NLLLoss的计算是不是一样
crossentropyloss = nn.CrossEntropyLoss()
crossentropyloss_output = crossentropyloss(x_input, y_target)
print('crossentropyloss_output:\n', crossentropyloss_output)
输出结果:
x_input:
tensor([[ 0.4674, 0.5112, -2.0071],
[-0.0689, 0.1019, -0.7187],
[ 1.5059, 0.5531, 0.1345]])
soft_output:
tensor([[0.4697, 0.4907, 0.0396],
[0.3692, 0.4380, 0.1928],
[0.6100, 0.2352, 0.1548]])
log_output:
tensor([[-0.7556, -0.7118, -3.2301],
[-0.9964, -0.8255, -1.6461],
[-0.4943, -1.4471, -1.8658]])
logsoftmax_output:
tensor([[-0.7556, -0.7118, -3.2301],
[-0.9964, -0.8255, -1.6461],
[-0.4943, -1.4471, -1.8658]])
nlloss_output:
tensor(0.9508)
crossentropyloss_output:
tensor(0.9508)
参考
交叉熵损失函数(Cross Entropy Loss)
【Pytorch】交叉熵损失函数 CrossEntropyLoss() 详解