图像归一化

1. 图像归一化

图像归一化是指对图像进行了一系列标准的处理变换，使之变换为一固定标准形式的过程，该标准图像称作归一化图像。

在机器学习中，不同评价指标（即特征向量中的不同特征，就是所述的不同评价指标）往往具有不同的量纲和量纲单位，这样的情况会影响到数据分析的结果。为了消除指标之间的量纲影响，需要进行数据标准化处理，以解决数据指标之间的可比性。原始数据经过数据标准化处理后，各指标处于同一数量级，适合进行综合对比评价。其中，最典型的就是数据的归一化处理。简而言之，归一化的目的就是使得预处理的数据被限定在一定的范围内（比如[0,1]或者[-1,1]），从而消除奇异样本数据导致的不良影响。

在深度学习中，通常在模型训练前都会对图像进行归一化处理，而对图像进行归一化处理是将特征值大小调整到相近的范围，不归一化处理时，如果特征值较大时，梯度值也会较大，特征值较小时，梯度值也会较小。在模型反向传播时，梯度值更新与学习率一样，当学习率较小时，梯度值较小会导致更新缓慢，当学习率较大时，梯度值较大会导致模型不易收敛，因此为了使模型训练收敛平稳，对图像进行归一化操作，把不同维度的特征值调整到相近的范围内，就可以采用统一的学习率加速模型训练。

2. 图像归一化的常用方法及Python应用

2.1 Min-Max归一化

通过遍历图像矩阵中的每一个像素，设定max和min，进行数据的归一化处理，公式如下：
$$x^{\prime }=(x-min(x))/(max(x)-min(x))$$
（1）线性函数将原始数据用线性化的方法转换到[0,1]的范围，计算结果x’为归一化后的数据，x为原始数据。（2）Min-Max归一化方法比较适用在数值比较集中的情况。
（3）缺点：如果max和min不稳定，很容易使得归一化结果不稳定，使得后续使用效果也不稳定。实际使用中可以用经验常量来替代max和min。

测试代码如下：

img = cv.imread('lenna.jpg')
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
h,w = gray.shape
mn = np.min(gray)
mx = np.max(gray)
norm = np.zeros((h,w),dtype=np.float32) # 自定义空白单通道图像，用于存放归一化图像
for i in range(h):
   for j in range(w):
       norm[i,j] = (gray[i,j] - mn) / (mx - mn)
       #norm[i,j] = gray[i,j] / 255

print('归一化前：')
print(gray)
print('归一化后：')
print(norm)

plt.subplot(121), plt.imshow(gray, 'gray'), plt.title('gray')
plt.axis('off')
plt.subplot(122), plt.imshow(norm, 'gray'), plt.title('normalization')
plt.axis('off')
plt.show()

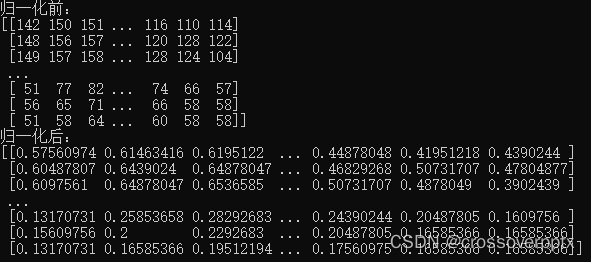
归一化前后灰度图像矩阵如下所示：

归一化前后灰度图像对比如下所示：

2.2 z-score标准化

z-score标准化公式如下：
$$x^{\prime }=(x-\mu )/\sigma$$
其中，μ、σ分别为原始数据集的均值和方法。
（1）将原始数据集归一化为均值为0、方差1的数据集。
（2）该种归一化方式要求原始数据的分布可以近似为高斯分布，否则归一化的效果会变得很糟糕。
（3）应用场景：在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，z-score standardization表现更好。

测试代码如下：

img = cv.imread('lenna.jpg')
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
h,w = gray.shape
x_mean = np.mean(gray)
vari = np.sqrt((np.sum((gray-x_mean)**2))/(h*w))
norm = np.zeros((h,w),dtype=np.float32) # 自定义空白单通道图像，用于存放归一化图像
for i in range(h):
   for j in range(w):
       norm[i,j] = (gray[i,j] - x_mean) / vari
       #norm[i,j] = gray[i,j] / 127.5 - 1

print('归一化前：')
print(gray)
print('归一化后：')
print(norm)

plt.subplot(121), plt.imshow(gray, 'gray'), plt.title('gray')
plt.axis('off')
plt.subplot(122), plt.imshow(norm, 'gray'), plt.title('normalization')
plt.axis('off')
plt.show()

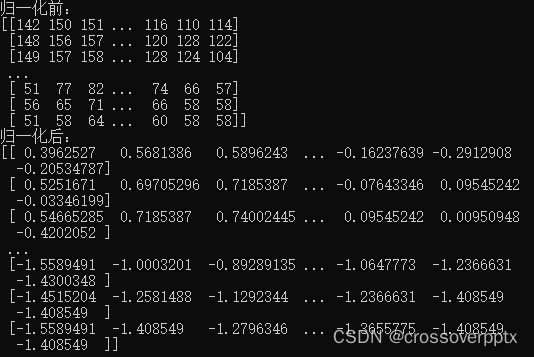
归一化前后灰度图像矩阵如下所示：

归一化前后灰度图像对比如下所示：

2.3 神经网络归一化

该归一化方法经常用在数据分化比较大的场景，有些数值很大，有些很小。通过一些数学函数，将原始值进行映射。该方法包括log，反正切等，需要根据数据分布的情况，决定非线性函数的曲线。

2.3.1 log对数函数归一化

y = log10(x)，即以10为底的对数转换函数，对应的归一化方法为：
$$x^{\prime }=log10(x)/log10(max)$$
其中max表示样本数据的最大值，并且所有样本数据均要大于等于1。

测试代码如下：

img = cv.imread('lenna.jpg')
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
h,w = gray.shape
norm = np.zeros((h,w),dtype=np.float32) # 自定义空白单通道图像，用于存放归一化图像
norm = np.log10(gray) / np.log10(gray.max())

print('归一化前：')
print(gray)
print('归一化后：')
print(norm)

plt.subplot(121), plt.imshow(gray, 'gray'), plt.title('gray')
plt.axis('off')
plt.subplot(122), plt.imshow(norm, 'gray'), plt.title('normalization')
plt.axis('off')
plt.show()

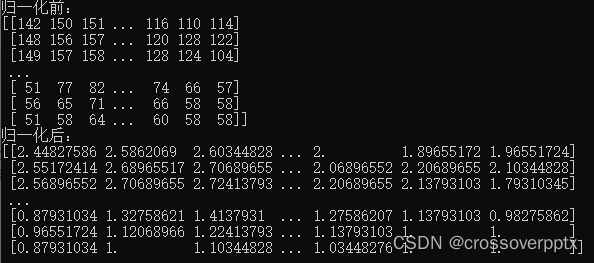
归一化前后灰度图像矩阵如下所示：

归一化前后灰度图像对比如下所示：

2.3.2 反正切函数归一化

对应的归一化方法为：x’ = atan(x)*(2/pi)

使用这个方法需要注意的是如果想映射的区间为[0,1]，则数据都应该大于等于0，小于0的数据将被映射到[－1,0]区间上。

测试代码如下：

img = cv.imread('lenna.jpg')
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
h,w = gray.shape
norm = np.zeros((h,w),dtype=np.float32) # 自定义空白单通道图像，用于存放归一化图像
norm = np.arctan(gray) * (2 / np.pi)

print('归一化前：')
print(gray)
print('归一化后：')
print(norm)

plt.subplot(121), plt.imshow(gray, 'gray'), plt.title('gray')
plt.axis('off')
plt.subplot(122), plt.imshow(norm, 'gray'), plt.title('normalization')
plt.axis('off')
plt.show()

归一化前后灰度图像矩阵如下所示：

归一化前后灰度图像对比如下所示：

2.4 L2范数归一化

定义：特征向量中每个元素均除以向量的范数，即如下公式：
$$x_i^{\prime }=x_i/(norm(x))$$
向量x(x1,x2,…,xn)的L2范数定义为：
$$norm(x)=\sqrt{(}{x}_1^2+x_2^2+\cdots +x_n^2)$$
测试代码如下：

img = cv.imread('lenna.jpg')
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
h,w = gray.shape
norm = np.zeros((h,w),dtype=np.float32) # 自定义空白单通道图像，用于存放归一化图像
for i in range(h):
   for j in range(w):
       norm_x = 0.0 + gray[i,j]**2
norm_x = np.sqrt(norm_x)
norm = gray / norm_x

print('归一化前：')
print(gray)
print('归一化后：')
print(norm)

plt.subplot(121), plt.imshow(gray, 'gray'), plt.title('gray')
plt.axis('off')
plt.subplot(122), plt.imshow(norm, 'gray'), plt.title('normalization')
plt.axis('off')
plt.show()

归一化前后灰度图像矩阵如下所示：

归一化前后灰度图像对比如下所示：

3. opencv-python中归一化方法的应用

opencv-python中使用cv2.normalize()函数实现归一化，其函数原型如下：

cv2.normalize(src[, dst[, alpha[, beta[, norm_type[, dtype[, mask]]]]]]) → dst

参数说明：
src：输入数组；
dst：输出数组，数组的大小和原数组一致；
alpha：1.用来规范值。2.规范范围，并且是下限；
beta：只用来规范范围并且是上限；
norm_type：归一化选择的数学公式类型；
dtype：当为负，输出在大小深度通道数都等于输入，当为正，输出只在深度与输入不同，不同的地方由dtype决定；
mark：掩码。选择感兴趣区域，选定后只能对该区域进行操作。

归一化选择的数学公式类型有如下几种：
NORM_MINMAX：数组的数值被平移或缩放到一个指定的范围，线性归一化，一般较常用；
NORM_INF：矩阵中绝对值的最大值；
NORM_L1：归一化数组的L1-范数(绝对值的和)；
NORM_L2：归一化数组的(欧几里德)L2-范数。

测试代码如下（以NORM_MINMAX为例）：

img = cv.imread('lenna.jpg')
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
h,w = gray.shape
norm = np.zeros((h,w),dtype=np.float32) # 自定义空白单通道图像，用于存放归一化图像
cv.normalize(gray, norm, alpha=0, beta=1, norm_type=cv.NORM_MINMAX, dtype=cv.CV_32F)

# norm = np.uint8(norm*255.0)

print('归一化前：')
print(gray)
print('归一化后：')
print(norm)

plt.subplot(121), plt.imshow(gray, 'gray'), plt.title('gray')
plt.axis('off')
plt.subplot(122), plt.imshow(norm, 'gray'), plt.title('normalization')
plt.axis('off')
plt.show()

归一化前后灰度图像矩阵如下所示，可以发现与2.1节Min-Max归一化处理结果一致：

归一化前后灰度图像对比如下所示：