力扣LeetCode刷题笔记总结2

 题型十三：二叉树

0.二叉树的基础知识

（1）二叉树的分类：

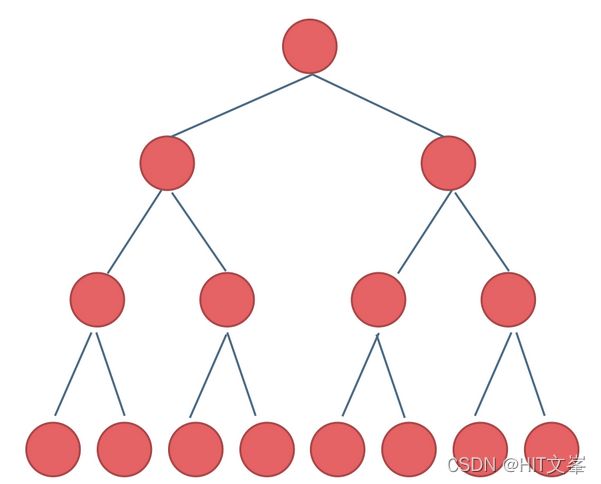
a. 满二叉树：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。

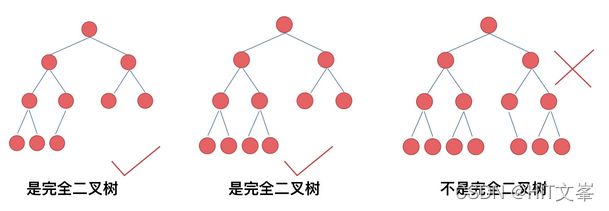
b.完全二叉树：除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。

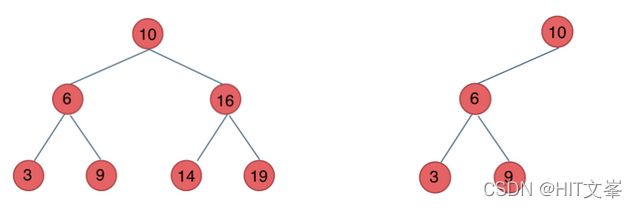
 c.二叉搜索树：不同于以上两种，二叉搜索树有数值，且数值有序。

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉排序树

d.平衡二叉搜索树 AVL：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

 

 （2）二叉树的存储方式：

• 链式存储
• 顺序存储：即用数组来存储二叉树，遍历数组中的树：如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。

 （3）二叉树的遍历 ：

• 深度优先遍历
  • 前序遍历（递归法，迭代法）
  • 中序遍历（递归法，迭代法）
  • 后序遍历（递归法，迭代法）
• 广度优先遍历
  • 层次遍历（迭代法）

 （4）二叉树的定义：

 struct TreeNode {
     int val;
     TreeNode *left;
     TreeNode *right;
     TreeNode() : val(0), left(nullptr), right(nullptr) {}
     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 };

 (5)  N叉树的定义：

class Node {
public:
    int val;
    vector children;
    Node() {}
    Node(int _val) { val = _val; }
    Node(int _val, vector _children) { val = _val;children = _children; }
}

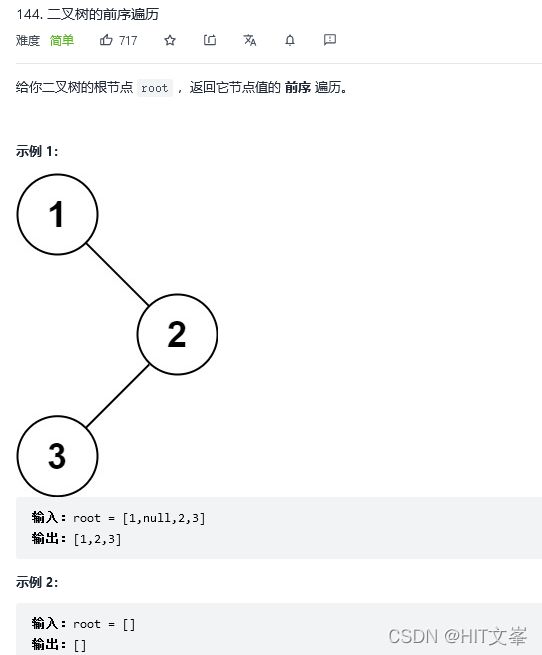
1. 二叉树的前序遍历

 

解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // 1、确定递归函数的参数和返回值   &nums必须按地址传递
    void Traversal(TreeNode *cur,vector &nums){
        //2、确定终止条件
        if(cur==nullptr) return;                          
        //3、确定单层递归的逻辑
        nums.push_back(cur->val);    //中
        Traversal(cur->left,nums);   //左
        Traversal(cur->right,nums);  //右
    }
    vector preorderTraversal(TreeNode* root) {
       vector ans;
       Traversal(root,ans);
       return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

• 空间复杂度：O(n)，为递归过程中栈的开销，平均情况下为 O(log⁡n)，最坏情况下树呈现链状，为 O(n)。

解法2：迭代

 区别：递归的时候隐式地维护了一个栈，而迭代的时候需要显式地将这个栈模拟出来，其余的实现与细节都相同

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector preorderTraversal(TreeNode* root) {
       vector ans;    //将元素放入ans数组中
       if(root==nullptr) return ans;
       stack stk;
       stk.push(root);       //中（根）
       while(!stk.empty()){
            TreeNode* node=stk.top();
            stk.pop();

            ans.push_back(node->val);                //中
            if(node->right)  stk.push(node->right);  //右，空节点不入栈
            if(node->left)  stk.push(node->left);    //左，空节点不入栈
       }
       return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

• 空间复杂度：O(n)，为迭代过程中栈的开销，平均情况下为 O(log⁡n)，最坏情况下树呈现链状，为 O(n)。

解法3：迭代（统一）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector preorderTraversal(TreeNode* root) {
     vector ans;
     stack stk;
     if(root!=nullptr) stk.push(root);
     while(!stk.empty()){
         TreeNode* node=stk.top();
         if(node!=nullptr){
             stk.pop();    //将根节点弹出，避免重复操作，，无此步，会超时

             if(node->right) stk.push(node->right);  //右
             if(node->left) stk.push(node->left);     //左
             stk.push(node);                          //中
             stk.push(nullptr);
         }
         else{
             stk.pop();
             node=stk.top();
             stk.pop();
             ans.push_back(node->val);
         }
     }
     return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

• 空间复杂度：O(n)，为迭代过程中栈的开销，平均情况下为 O(log⁡n)，最坏情况下树呈现链状，为 O(n)。

2.二叉树的中序遍历

 解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void Traversal(TreeNode *node,vector &vec){
        if(node==nullptr) return;
        Traversal(node->left,vec);
        vec.push_back(node->val);
        Traversal(node->right,vec);
    }
    vector inorderTraversal(TreeNode* root) {
        vector ans;
        Traversal(root,ans);
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

• 空间复杂度：O(n)，为递归过程中栈的开销，平均情况下为 O(log⁡n)，最坏情况下树呈现链状，为 O(n)。

解法2：迭代

使用栈，此法的迭代和前序后序不能统一，因为访问节点（遍历节点）和处理节点（将元素放入结果集）无法同时解决。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector inorderTraversal(TreeNode* root) {
       stack stk;
       vector ans;
       TreeNode* node=root;
       while(node!=nullptr || !stk.empty()){
           if(node!=nullptr){
               stk.push(node);   //指针访问节点，访问到最底层，将访问的节点放入栈中
               node=node->left;  //左
           }
           else{
               //栈中弹出的数据就是要处理的数据，即要放入ans数组里的数据
               node=stk.top();
               stk.pop();
               ans.push_back(node->val);  //中               
               node=node->right;          //右
           }
       }
       return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

• 空间复杂度：O(n)，为迭代过程中栈的开销，平均情况下为 O(log⁡n)，最坏情况下树呈现链状，为 O(n)。

解法3：迭代（统一）

将要处理的节点放入栈之后，紧接着放入一个空指针作为标记

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector inorderTraversal(TreeNode* root) {
     vector ans;  //存放结果
     stack stk;
     if(root!=nullptr) stk.push(root);  //将根节点放入栈中
     while(!stk.empty()){
         TreeNode* node = stk.top();   //取出栈中元素
         if(node!=nullptr){
             stk.pop();             //将节点弹出，避免重复操作
             if(node->right) stk.push(node->right);  //右  空节点不入栈
             stk.push(node);        //中
             stk.push(nullptr);     //中节点访问过，但是还没有处理， 加入空节点做标记
             if(node->left)   stk.push(node->left);  //左  空节点不入栈
         }

         else{
             //空节点做的标记，只有遇到空节点时，才将下一个节点放入结果集
             stk.pop();        //将空节点弹出
             node=stk.top();   //重新取出栈中元素
             stk.pop();
             ans.push_back(node->val);  //加入到结果集
         }
     }
     return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

• 空间复杂度：O(n)，为迭代过程中栈的开销，平均情况下为 O(log⁡n)，最坏情况下树呈现链状，为 O(n)。

3.二叉树的后序遍历

 解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void Traversal(TreeNode *root,vector &vec){
        if(root==nullptr) return;
        Traversal(root->left,vec);    //是root->left,而不是vec->left
        Traversal(root->right,vec);
        vec.push_back(root->val);
    }
    vector postorderTraversal(TreeNode* root) {
        vector ans;       //ans用于存放遍历后的二叉树
        Traversal(root,ans);
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

• 空间复杂度：O(n)，为递归过程中栈的开销，平均情况下为 O(log⁡n)，最坏情况下树呈现链状，为 O(n)。

 解法2：迭代

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector postorderTraversal(TreeNode* root) {
       vector ans;
       if(root==nullptr) return ans;
       stack stk;
       stk.push(root);
       while(!stk.empty()){
           TreeNode* node=stk.top();
           stk.pop();

           ans.push_back(node->val);
           if(node->left) stk.push(node->left);  //相对于前序遍历，这更改一下入栈顺序
           if(node->right) stk.push(node->right);
       }
       reverse(ans.begin(),ans.end());
       return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

• 空间复杂度：O(n)，为迭代过程中栈的开销，平均情况下为 O(log⁡n)，最坏情况下树呈现链状，为 O(n)。

 解法3：迭代（统一）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector postorderTraversal(TreeNode* root) {
      stack stk;
      vector ans;
      if(root!=nullptr)  stk.push(root);
      while(!stk.empty()){
          TreeNode* node=stk.top();
          if(node!=nullptr){
              stk.pop();       //将该节点弹出，避免重复操作
              stk.push(node);
              stk.push(nullptr);
              if(node->right)  stk.push(node->right);
              if(node->left)   stk.push(node->left);
          }
          else{
              stk.pop();      //将空节点弹出
              node=stk.top();
              stk.pop();
              ans.push_back(node->val);
          }
      }
      return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

• 空间复杂度：O(n)，为迭代过程中栈的开销，平均情况下为 O(log⁡n)，最坏情况下树呈现链状，为 O(n)。

4.#二叉搜索树的后序遍历序列

 

 解法1：递归

class Solution {
private:
    bool Traversal(vector& postorder,int i,int j){
        if(i>=j) return true;  // 此子树节点数量 ≤1，无需判别正确性，因此直接返回 true
        //寻找第一个大于根节点的节点，切分数组
        int p=i;
        while(postorder[p]postorder[j]) p++;

        //根节点p=j; 左子树[i,m-1]; 右子树[m,j-1]
        return p==j && Traversal(postorder,i,m-1) && Traversal(postorder,m,j-1);
    }
public:
    bool verifyPostorder(vector& postorder) {
        return Traversal(postorder,0,postorder.size()-1);
    }
};

• 时间复杂度：O(n^2)，其中 n 是二叉树的节点数。每次调用 Traversal(i,j) 减去一个根节点，因此递归占用 O(n) ；最差情况下（即当树退化为链表），每轮递归都需遍历树所有节点，占用 O(n)。

• 空间复杂度：O(n)，最差情况下（即当树退化为链表），递归深度将达到 n。

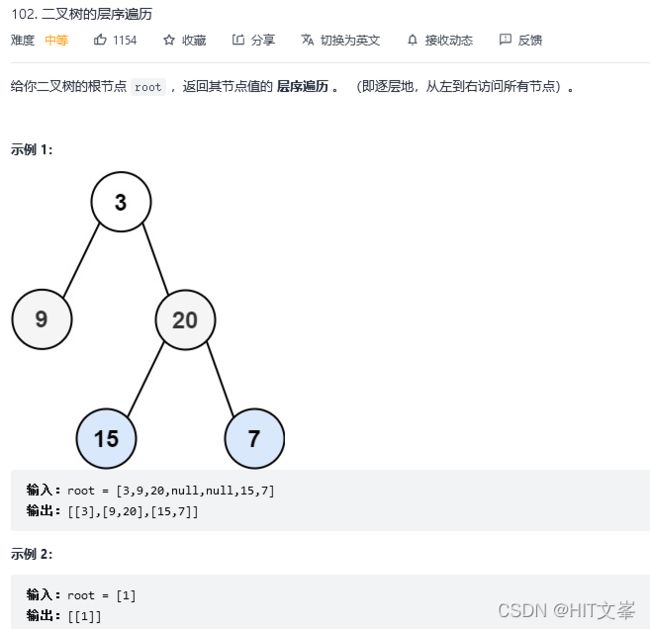
5.二叉树的层序遍历

 

解法1：广度优先搜索

 思路：一旦出现树的层序遍历，都可以用队列作为辅助结构。队列先进先出，符合一层一层遍历的逻辑，而是用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。

（1）首先根元素入队

（2）当队列不为空的时候：求当前队列的长度 si；依次从队列中取 si​ 个元素进行拓展，然后进入下一次迭代。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector> levelOrder(TreeNode* root) {
        vector> ans;
        queue que;         //队列先进先出，符合一层一层遍历的逻辑,故使用队列实现二叉树广度优先遍历,,,,,元素为二叉树
        if(root!=nullptr) que.push(root);

        while(!que.empty()){
            vector vec;
            int size=que.size();
            for(int i=0;ival);   //容器中放进值
                if(node->left)  que.push(node->left);     //队列中放入
                if(node->right) que.push(node->right);    //错误代码 vec.push(),  que_push_back()
            }
            ans.push_back(vec);
       }
       return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点进出队列各一次。

• 空间复杂度：O(n)，队列中元素个数不超过n。

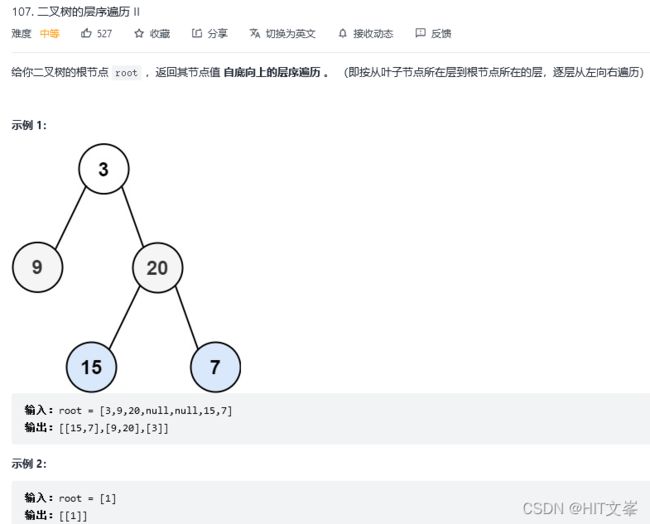
6.二叉树的层次遍历II

解法1：广度优先搜索 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector> levelOrderBottom(TreeNode* root) {
        vector>  ans;
        queue que;
        if(root!=nullptr) que.push(root);
        while(!que.empty()){
            vector vec;
            int size=que.size();
            for(int i=0;ival);
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            ans.push_back(vec);
        }
        reverse(ans.begin(),ans.end());  //不同：反转一下数组即可
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点进出队列各一次。

• 空间复杂度：O(n)，空间复杂度取决于队列开销，队列中元素个数不超过n。

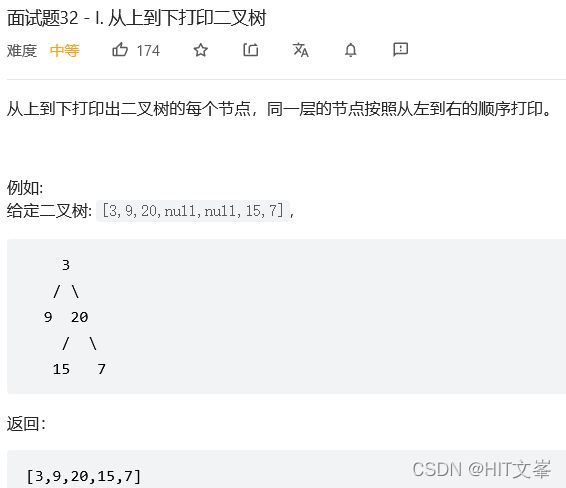
7.#从上到下打印二叉树

 

 解法1：广度优先搜索

class Solution {
public:
    vector levelOrder(TreeNode* root) {
        vector ans;
        queue que;
        if(root!=NULL) que.push(root);
        while(!que.empty()){           
            int size=que.size();
            for(int i=0;ival);
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
        }
        return ans;
    }
};

8.#从上到下打印二叉树II

 

 解法1：广度优先搜索

class Solution {
public:
    vector> levelOrder(TreeNode* root) {
        vector> ans;
        queue que;
        if(root!=NULL) que.push(root);
        while(!que.empty()){
            vector vec;
            int size=que.size();
            for(int i=0;ival);
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            ans.push_back(vec);
        }
        return ans;
    }
};

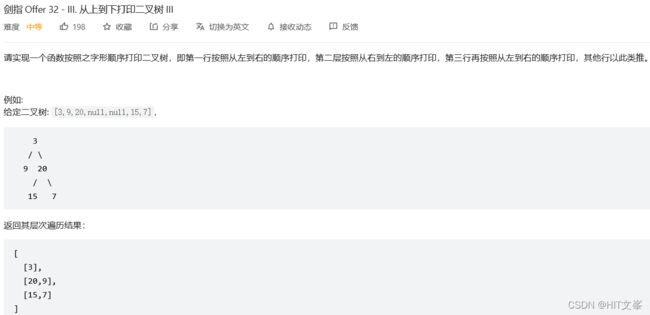
9.#从上到下打印二叉树III

 

 解法1：广度优先搜索

class Solution {
public:
    vector> levelOrder(TreeNode* root) {
        vector> ans;
        queue que;
        if(root!=NULL) que.push(root);
        while(!que.empty()){
            vector vec;
            int size=que.size();
            for(int i=0;ival);
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            // 若 ans 的长度为 奇数 ，说明当前是偶数层，则对 vec 执行 倒序 操作。
            if(ans.size()%2==1) reverse(vec.begin(),vec.end());
            ans.push_back(vec);
        }
        return ans;
    }
};

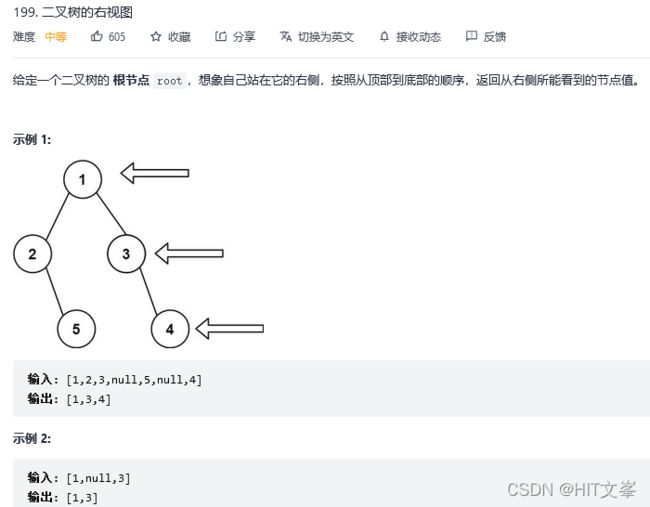
10.二叉树的右视图

 解法1：广度优先搜索

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector rightSideView(TreeNode* root) {
        vector ans;
        queue que;
        if(root!=nullptr) que.push(root);
        while(!que.empty()){
            int size=que.size();
            for(int i=0;ival);  //将每一层的最后一个元素放入ans数组中,之前是所有的元素全部放入数组中

                 if(node->left) que.push(node->left);
                 if(node->right) que.push(node->right);
           }
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点进出队列各一次。

• 空间复杂度：O(n)，空间复杂度取决于队列开销，队列中元素个数不超过n。

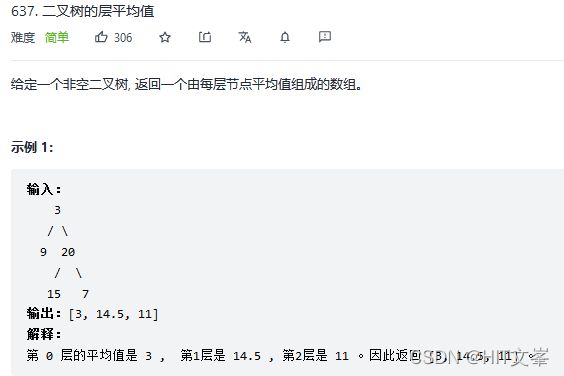
11.二叉树的层平均值

解法1：广度优先搜索

class Solution {
public:
    vector averageOfLevels(TreeNode* root) {
        vector ans;
        queue que;
        if(root!=nullptr) que.push(root);
        while(!que.empty()){
            int size=que.size();
            double sum=0;   // 统计每一层的和
            for(int i=0;ival;
          
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            ans.push_back(sum/size);   将每一层均值放进结果集，不是除以que.size()
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点进出队列各一次。需要对二叉树的每一层计算平均值，时间复杂度是 O(h)，其中 h 是二叉树的高度，任何情况下都满足 h≤n。因此总时间复杂度是 O(n)。

• 空间复杂度：O(n)，空间复杂度取决于队列开销，队列中元素个数不超过n。

12.在每个树行中找最大值

 解法1：广度优先搜索

class Solution {
public:
    vector largestValues(TreeNode* root) {
        vector ans;
        queue que;
        if(root!=nullptr) que.push(root);
        while(!que.empty()){
            int size=que.size();
            int maxValue=INT_MIN;
            for(int i=0;ival >maxValue? node->val :maxValue;
                // maxValue=max(node->val,maxValue);

                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            ans.push_back(maxValue);
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点进出队列各一次。

• 空间复杂度：O(n)，空间复杂度取决于队列开销，队列中元素个数不超过n。

解法2：广度优先搜索（sort排序）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector largestValues(TreeNode* root) {
     vector ans;
     queue que;
     if(root!=nullptr) que.push(root);
     while(!que.empty()){
         int size=que.size();
         vector vec;
         for(int i=0;ival);
             if(node->left) que.push(node->left);
             if(node->right) que.push(node->right);
         }
         sort(vec.begin(),vec.end(),greater());
         ans.push_back(vec[0]);
     }
     return ans;
    }
};

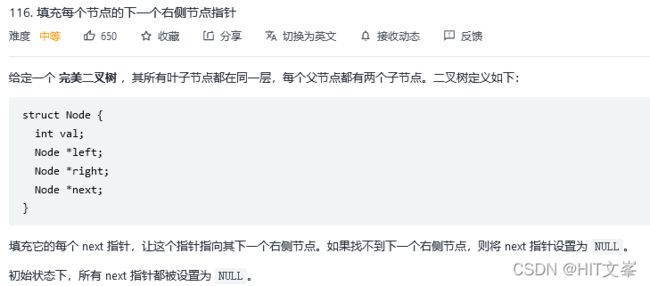
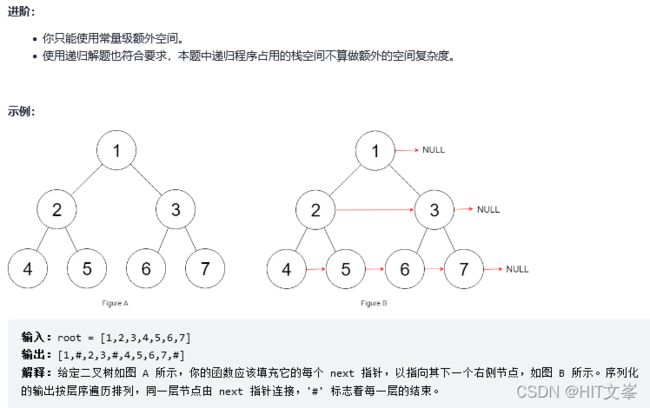
13.填充每个节点的下一个右侧节点指针

 解法1：广度优先搜索

/*// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;
    Node() : val(0), left(NULL), right(NULL), next(NULL) {}
    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};*/

class Solution {
public:
    Node* connect(Node* root) {
        queue que;
        if(root!=NULL) que.push(root);

        while(!que.empty()){                // 1、外层的 while 循环迭代的是层数
            int size=que.size();            // 记录当前队列大小           
            for(int i=0; inext = que.front();   // 连接
                
                if(node->left)  que.push(node->left);
                if(node->right) que.push(node->right);
            }
        }
        return root;
    }
};

• 时间复杂度：O(n)，每个节点会被访问一次且只会被访问一次，即从队列中弹出，并建立 next 指针。

• 空间复杂度：O(n)，这是一棵完美二叉树，它的最后一个层级包含 n/2 个节点。广度优先遍历的复杂度取决于一个层级上的最大元素数量。这种情况下空间复杂度为 O(n)。

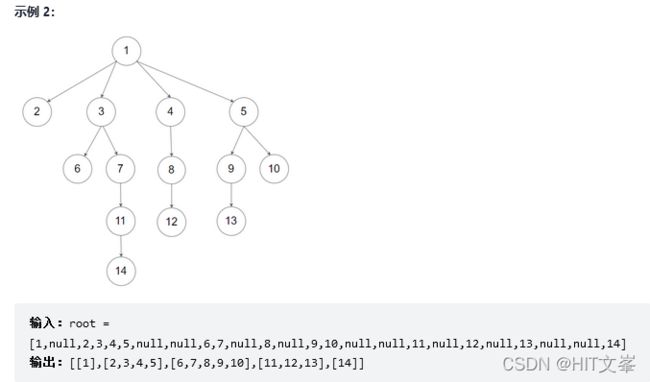
14.填充每个节点的下一个右侧节点指针II

 解法1：广度优先搜索

class Solution {
public:
    Node* connect(Node* root) {
        queue que;
        if(root!=NULL) que.push(root);

        while(!que.empty()){                // 1、外层的 while 循环迭代的是层数
            int size=que.size();            // 记录当前队列大小           
            for(int i=0; inext = que.front();
                }else{
                    node->next = NULL;
                }
                
                if(node->left)  que.push(node->left);
                if(node->right) que.push(node->right);
            }
        }
        return root;
    }
};

• 时间复杂度：O(n)，每个节点会被访问一次且只会被访问一次，即从队列中弹出，并建立 next 指针。

• 空间复杂度：O(n)，空间复杂度取决于队列开销，队列中元素个数不超过n。

15.N叉树的层序遍历

 

解法1：广度优先搜索

/*// Definition for a Node.
class Node {
public:
    int val;
    vector children;
    Node() {}
    Node(int _val) {
        val = _val;
    }
    Node(int _val, vector _children) {
        val = _val;
        children = _children;
    }
};*/
class Solution {
public:
    vector> levelOrder(Node* root) {
        vector> ans;
        queue que;
        if(root!=nullptr) que.push(root);
        while(!que.empty()){
            vector vec;
            int size=que.size();
            for(int i=0;ival);   //传入val,而不是_val

                //将节点孩子加入队列
                for(int i=0;ichildren.size();++i){
                    if(node->children[i])   que.push(node->children[i]);
                }
            }
            ans.push_back(vec);
        }
        return ans ;
    }
};

• 时间复杂度：O(n)，其中 n 是N叉树的节点数。每一个节点进出队列各一次。

• 空间复杂度：O(n)，空间复杂度取决于队列开销，队列中元素个数不超过n。

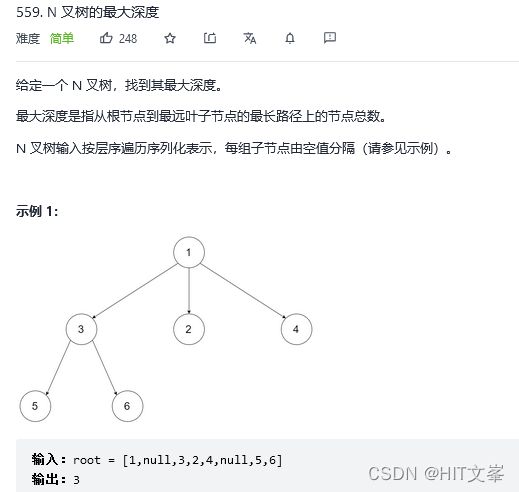
16.二叉树的最大深度

  解法1：广度优先搜索（迭代）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    //层序遍历的层数就是二叉树的最大深度
    int maxDepth(TreeNode* root) {
       if(root==nullptr)  return 0;
       int depth=0;
       queue que;
       que.push(root);
       while(!que.empty()){
           int size=que.size();
           depth++;  //记录深度
           for(int i=0;ileft) que.push(node->left);
               if(node->right) que.push(node->right);
           }
       }
       return depth;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点进出队列各一次。

• 空间复杂度：O(n)，空间复杂度取决于队列开销，队列中元素个数不超过n。

解法2：深度优先搜索 （递归）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * }; */
class Solution {
public:
    int getDepth(TreeNode *root){
        if(root==nullptr) return 0;
        int leftDepth  = getDepth(root->left);
        int rightDepth = getDepth(root->right);
        return 1+max(leftDepth,rightDepth);
    }
    int maxDepth(TreeNode* root) {
        return getDepth(root);
    }
};
/*   //简化
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root==nullptr)  return 0;
        return 1+max(maxDepth(root->left),maxDepth(root->right));
    }
}; */

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每个节点在递归中只被遍历一次。

• 空间复杂度：O(h)，其中 h 表示二叉树的高度。递归函数需要栈空间，而栈空间取决于递归的深度，因此空间复杂度等价于二叉树的高度。

17.#二叉树的深度

 解法1：递归

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root==NULL) return 0;
        return 1+max(maxDepth(root->left),maxDepth(root->right));
    }
};

18. N叉树的最大深度

 解法1：广度优先搜索（迭代）

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector children;
    Node() {}
    Node(int _val) {
        val = _val;
    }
    Node(int _val, vector _children) {
        val = _val;
        children = _children;
    }
};*/

class Solution {
public:
    int maxDepth(Node* root) {
        if(root==nullptr) return 0;    
        int depth=0;
        queue que;
        que.push(root);
        while(!que.empty()){
            int size=que.size();
            depth++;
            for(int i=0;ichildren.size();++i){
                    if(node->children[i]) que.push(node->children[i]);
                }
            }
        }
        return depth;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点进出队列各一次。

• 空间复杂度：O(n)，空间复杂度取决于队列开销，队列中元素个数不超过n。

解法2：深度优先搜索 （递归） 

思路：记 n 个子树的最大深度中的最大值为 maxChildDepth，则该 n 叉树的最大深度为 maxChildDepth+1。

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector children;
    Node() {}
    Node(int _val) {
        val = _val;
    }
    Node(int _val, vector _children) {
        val = _val;
        children = _children;
    }
};*/

class Solution {
public:
    int maxDepth(Node* root) {
        if(root==nullptr) return 0;    
        int maxChildDepth=0;
        vector children=root->children;
        for(auto child : children){
            maxChildDepth=max(maxChildDepth,maxDepth(child));
        }
        return 1+maxChildDepth;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每个节点在递归中只被遍历一次。

• 空间复杂度：O(h)，其中 h 表示二叉树的高度。递归函数需要栈空间，而栈空间取决于递归的深度，因此空间复杂度等价于二叉树的高度。

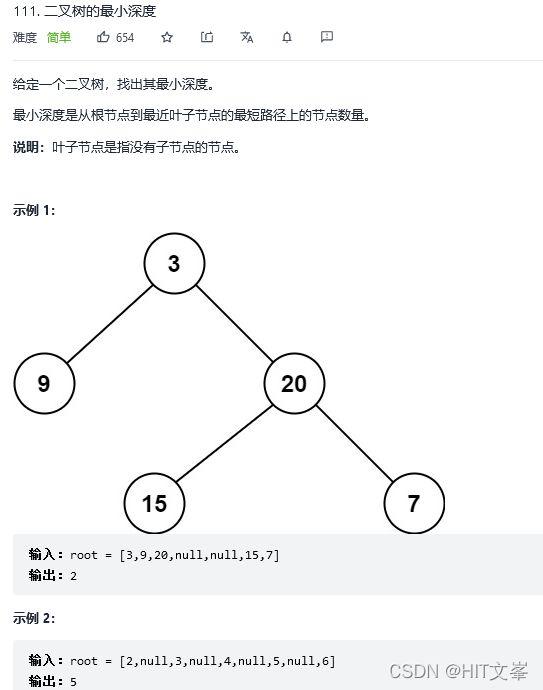
19.二叉树的最小深度

 解法1：广度优先搜索 （迭代）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {
public:
    int minDepth(TreeNode* root) {
      if(root==nullptr) return 0;
      int depth=0;
      queue que;
      que.push(root);
      while(!que.empty()){
         int size=que.size();
         depth++;
         for(int i=0;ileft) que.push(node->left);
             if(node->right) que.push(node->right);
             //遇到左右孩子为空，就找到了最小深度，就会提前return
             if(!node->left && !node->right) return depth;    
         }
      }
      return depth;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点进出队列各一次。

• 空间复杂度：O(n)，空间复杂度取决于队列开销，队列中元素个数不超过n。

 解法2：深度优先搜索 （递归）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root==nullptr) return 0;
        if(root->left==nullptr && root->right!=nullptr) 
        return 1+minDepth(root->right);
        if(root->left!=nullptr && root->right==nullptr)
        return 1+minDepth(root->left);

        return 1+min(minDepth(root->left),minDepth(root->right));
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每个节点在递归中只被遍历一次。

• 空间复杂度：O(h)，其中 h 表示二叉树的高度。递归函数需要栈空间，而栈空间取决于递归的深度，因此空间复杂度等价于二叉树的高度。最坏情况下，树呈现链状，空间复杂度为O(n)。

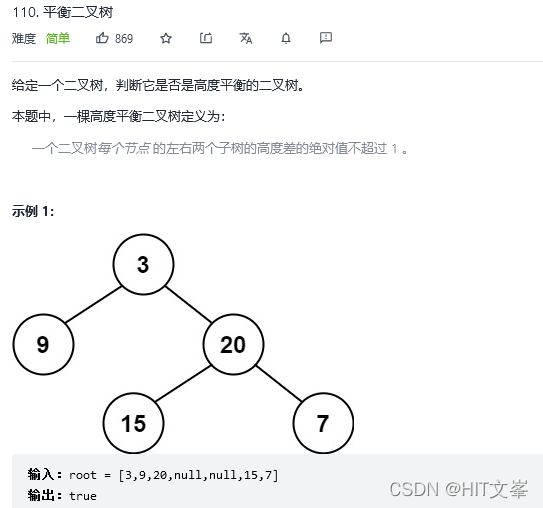
20.平衡二叉树

 

 解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution { 
public:
    //返回以该节点为根节点的二叉树的高度，如果不是平衡二叉树则返回-1
    int getHeight(TreeNode* node){
        if(node==nullptr) return 0;
        if(getHeight(node->left)==-1 || getHeight(node->right)==-1 || abs(getHeight(node->left)-getHeight(node->right))>1)  return -1;
        else return 1+max(getHeight(node->left),getHeight(node->right)); // 以当前节点为根节点的树的最大高度

        //if(getHeight(node->left)==-1) return -1;
        //if(getHeight(node->right)==-1) return -1;

        //if(abs(getHeight(node->left)-getHeight(node->right))>1) return -1;
        //else return 1+max(getHeight(node->left),getHeight(node->right));    
        //return abs(getHeight(node->left)-getHeight(node->right))>1 ? -1 : 1+max(getHeight(node->left),getHeight(node->right));
    }
    bool isBalanced(TreeNode* root) {
      return getHeight(root)>=0;
      //return getHeight(root)==-1?false:true;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树中的节点个数。使用自底向上的递归，每个节点的计算高度和判断是否平衡都只需要处理一次，最坏情况下需要遍历二叉树中的所有节点，因此时间复杂度是 O(n)。
• 空间复杂度：O(n)，其中 n 是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数，递归调用的层数不会超过 n。

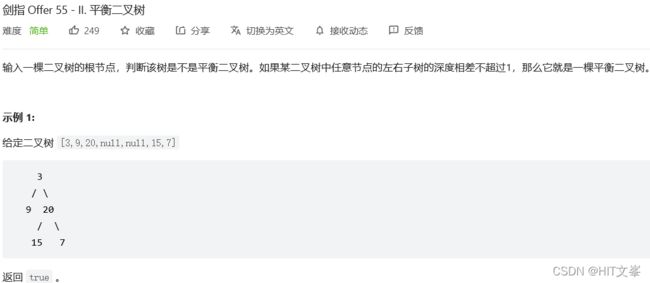
21.#平衡二叉树

 解法1：递归

class Solution {
private:
    int getHeight(TreeNode* root){
        if(root==NULL) return 0;
        int leftHeight=getHeight(root->left);
        int rightHeight=getHeight(root->right);
        if(leftHeight==-1||rightHeight==-1||abs(leftHeight-rightHeight)>1){
            return -1;
        }else{
            return 1+max(leftHeight,rightHeight);
        }
    }
public:
    bool isBalanced(TreeNode* root) {
        return getHeight(root)>=0;
    }
};

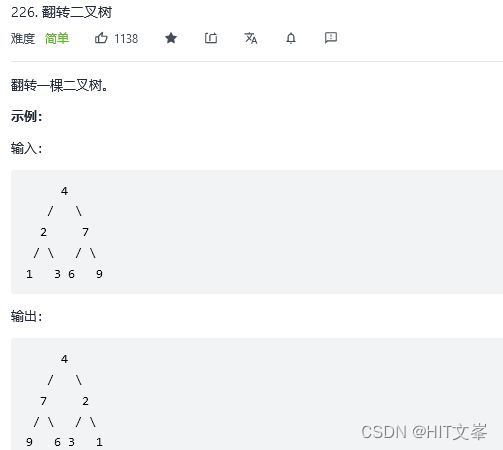
22.翻转二叉树

解法1：广度优先搜索

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/ 
class Solution {   
public:
    TreeNode* invertTree(TreeNode* root) {
      queue que;
      if(root!=nullptr) que.push(root);
      while(!que.empty()){
         int size=que.size();
         for(int i=0;ileft,node->right);
             if(node->left)  que.push(node->left);
             if(node->right) que.push(node->right);
         }
      }
      return root;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点进出队列各一次。

• 空间复杂度：O(n)，空间复杂度取决于队列开销，队列中元素个数不超过n。

解法2：递归（前序和后序）

 前序遍历和后序遍历可以，中序遍历不可以，因为中序遍历会把某些节点的左右孩子翻转两次

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution { 
public:   
    //递归三部曲：1、确定递归函数的参数和返回值
    TreeNode* invertTree(TreeNode* root) {
        //2、确定终止条件
        if(root==nullptr) return root;    
        //3、确定单层循环逻辑
        swap(root->left,root->right);    //中
        invertTree(root->left);          //左
        invertTree(root->right);         //右
        return root;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。我们会遍历二叉树中的每一个节点，对每个节点而言，我们在常数时间内交换其两棵子树。

• 空间复杂度：O(h)，其中 h 表示二叉树的高度。递归函数需要栈空间，而栈空间取决于递归的深度，因此空间复杂度等价于二叉树的高度。最坏情况下，树呈现链状，空间复杂度为O(n)。

解法3：迭代（前序）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/ 
class Solution { 
public:
    TreeNode* invertTree(TreeNode* root) {
      stack stk;
      if(root!=nullptr) stk.push(root);
      while(!stk.empty()){
         TreeNode *node=stk.top();  //取出栈顶元素
         if(node!=nullptr){
             stk.pop();      //将该节点弹出，避免重复操作
             if(node->right) stk.push(node->right); //右
             if(node->left) stk.push(node->left);   //左

             stk.push(node);                        //中  不是node->val
             stk.push(nullptr);
         }else{
             stk.pop();      //将空节点弹出
             node=stk.top(); //再次取出栈顶元素
             stk.pop();
             swap(node->left,node->right);    //交换左右节点
         }
      }
      return root;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。

• 空间复杂度：O(n)，为迭代过程中栈的开销，平均情况下为 O(log⁡n)，最坏情况下树呈现链状，为 O(n)

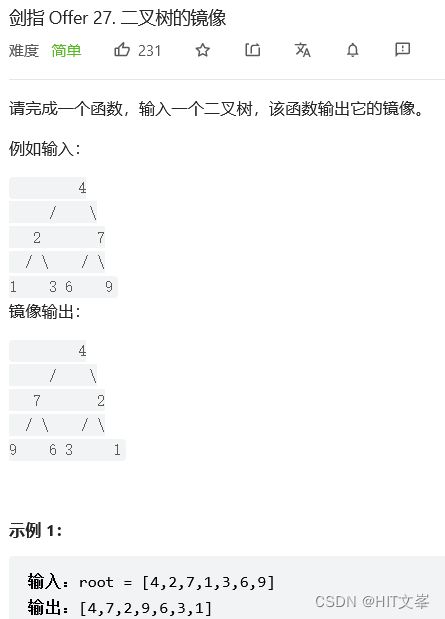
23.#二叉树的镜像

 解法1：递归

class Solution {
public:
    TreeNode* mirrorTree(TreeNode* root) {
        if(root==NULL) return root;
        swap(root->left,root->right);
        mirrorTree(root->left);
        mirrorTree(root->right);
        return root;
    }
};

 解法2：广度优先搜索（队列）

class Solution {
public:
    TreeNode* mirrorTree(TreeNode* root) {
        queue que;
        if(root!=NULL) que.push(root);
        while(!que.empty()){
            int n=que.size();
            for(int i=0;ileft,node->right);
                if(node->left)  que.push(node->left);
                if(node->right) que.push(node->right);
            }
        }
        return root;
    }
};

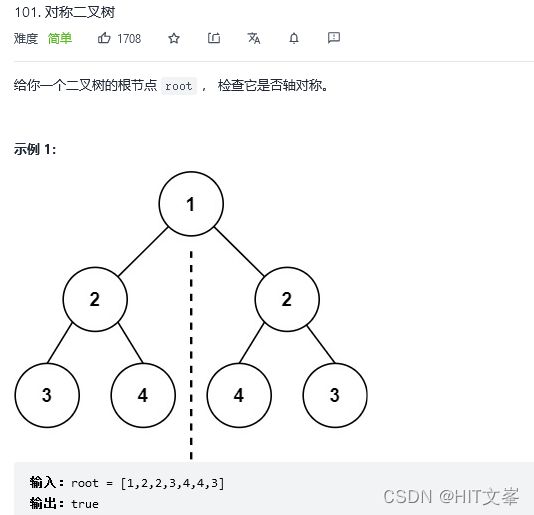
24.对称二叉树

解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * }; */
class Solution {
public:
    //递归三部曲：1、确定递归函数的参数和返回值
    bool compare(TreeNode* left,TreeNode *right){   
         //2、确定终止条件
         // 首先排除空节点的情况
        if (left == nullptr && right != nullptr) return false;
        else if (left != nullptr && right == nullptr) return false;
        else if (left == nullptr && right == nullptr) return true;
        // 排除了空节点，再排除数值不相同的情况
        else if (left->val != right->val) return false;
        // 此时就是：左右节点都不为空，且数值相同的情况，此时才做递归，做下一层的判断
        //3、确定单层递归逻辑
        else return compare(left->left, right->right) && compare(left->right, right->left);
        //等价于以下三行       
        //bool outside=compare(left->left,right->right);
        //bool inside=compare(left->right,right->left);
        //bool isSame=outside&&inside;        
    }
    bool isSymmetric(TreeNode* root) {
       if(root==nullptr) return true;
       return compare(root->left,root->right);
    }
};

class Solution {
public:
    //递归三部曲：1、确定递归函数的参数和返回值
    bool compare(TreeNode* left,TreeNode *right){   
        //2、确定终止条件
        if (left == nullptr && right == nullptr) return true;
        if (left == nullptr || right == nullptr) return false;
        //3、确定单层递归逻辑
        return left->val == right->val && compare(left->left, right->right) && compare(left->right, right->left);       
    }
    bool isSymmetric(TreeNode* root) {
      //if(root==nullptr) return true;
      return compare(root->left,root->right);
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。

• 空间复杂度：O(n)，递归函数需要栈空间，这里递归层数不超过 n，故渐进空间复杂度O(n)。

解法2：迭代

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (root == nullptr) return true;        
        queue que;
        que.push(root->left);   // 将左子树头结点加入队列
        que.push(root->right);  // 将右子树头结点加入队列        
        while (!que.empty()) {  // 接下来就要判断这两个树是否相互翻转
            TreeNode* leftNode = que.front(); que.pop();
            TreeNode* rightNode = que.front(); que.pop();
            if (!leftNode && !rightNode) {  // 左节点为空、右节点为空，此时说明是对称的
                continue;
            }

            // 左右一个节点不为空，或者都不为空但数值不相同，返回false
            if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
                return false;
            }
            que.push(leftNode->left);   // 加入左节点左孩子
            que.push(rightNode->right); // 加入右节点右孩子
            que.push(leftNode->right);  // 加入左节点右孩子
            que.push(rightNode->left);  // 加入右节点左孩子
        }
        return true;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。

• 空间复杂度：O(n)，为迭代过程中队列的开销，每个节点进出队列一次，队列中最多不会超过 n 个点，故渐进空间复杂度为 O(n)。

25.#对称的二叉树

 

 解法1：递归

class Solution {
public:
    bool compare(TreeNode* left,TreeNode* right){
        if(!left && !right) return true;
        if(!left || !right) return false;
        return left->val==right->val && compare(left->left,right->right) && compare(left->right,right->left);
    }
    bool isSymmetric(TreeNode* root) {
        if(root==NULL) return true;
        return compare(root->left,root->right);
    }
};

26. 相同的树

 

 解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
      if(!p && !q) return true;
      else if(p==nullptr||q==nullptr) return false;
      //else if(p==nullptr && q!=nullptr) return false;
      //else if(p!=nullptr && q==nullptr) return false;
      else return p->val==q->val && isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
    }
};

• 时间复杂度：O(min(m,n))，其中 m 和 n 分别是两个二叉树的节点数。对两个二叉树同时进行深度优先搜索，只有当两个二叉树中的对应节点都不为空时才会访问到该节点，因此被访问到的节点数不会超过较小的二叉树的节点数。

• 空间复杂度：O(min⁡(m,n))，其中 m 和 n 分别是两个二叉树的节点数。空间复杂度取决于递归调用的层数，递归调用的层数不会超过较小的二叉树的最大高度，最坏情况下，二叉树的高度等于节点数。

 解法2：迭代

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
      if (p==nullptr && q==nullptr) return true;     
        queue que;
        que.push(p);   // 将左根结点加入队列
        que.push(q);   // 将右根结点加入队列
        
        while (!que.empty()) {  // 接下来就要判断这两个树是否相同
            TreeNode* leftNode = que.front(); que.pop();
            TreeNode* rightNode = que.front(); que.pop();
            if (!leftNode && !rightNode) {  // 左节点为空、右节点为空，此时说明是对称的
                continue;
            }

            // 左右一个节点不为空，或者都不为空但数值不相同，返回false
            if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
                return false;
            }
            que.push(leftNode->left);    // 加入左节点左孩子
            que.push(rightNode->left);   // 加入右节点右孩子
            que.push(leftNode->right);   // 加入左节点右孩子
            que.push(rightNode->right);  // 加入右节点左孩子
        }
        return true;
    }
};

• 时间复杂度：O(min(m,n))，其中 m 和 n 分别是两个二叉树的节点数。对两个二叉树同时进行广度优先搜索，只有当两个二叉树中的对应节点都不为空时才会访问到该节点，因此被访问到的节点数不会超过较小的二叉树的节点数。

• 空间复杂度：O(min⁡(m,n))，其中 m 和 n 分别是两个二叉树的节点数。空间复杂度取决于队列中的元素个数，队列中的元素个数不会超过较小的二叉树的节点数。

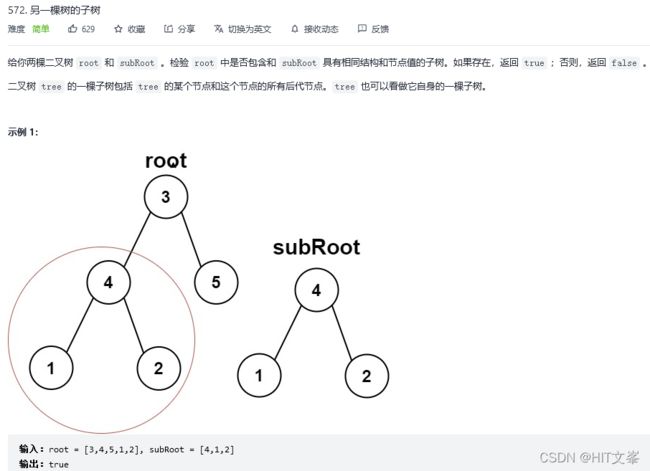
27.另一棵树的子树

 解法1：深度优先搜索（递归）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {   //深度优先搜索暴力匹配
public:
    bool check(TreeNode *s,TreeNode *t){
        if(!s && !t) return true;   //全空
        if(!s || !t) return false;
        return s->val == t->val && check(s->left,t->left) && check(s->right,t->right);
    }
    
    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        if(!root) return false;
        return check(root,subRoot) || isSubtree(root->left,subRoot) ||isSubtree(root->right,subRoot);
    }
};

• 渐进时间复杂度： O(∣s∣×∣t∣)，对于每一个 s 上的点，都需要做一次深度优先搜索来和 t 匹配，匹配一次的时间代价是 O(∣t∣)，那么总的时间代价就是 O(∣s∣×∣t∣)。

• 渐进空间复杂度： O(max⁡{ds,dt})，假设 s 深度为 ds​，t 的深度为 dt​，任意时刻栈空间的最大使用代价是 O(max⁡{ds,dt})。

28.#树的子结构

 解法1：深度优先搜索

思路：与“另一棵树的子树” 不同的是，子树不一定包含母树的一个节点后的所有节点

class Solution {
public:
    bool check(TreeNode *s,TreeNode *t){
        if(!t) return true;   
        if(!s) return false;
        return s->val == t->val && check(s->left,t->left) && check(s->right,t->right);
    }
    bool isSubStructure(TreeNode* A, TreeNode* B) {
        if(!A || !B) return false;
        return check(A,B)||isSubStructure(A->left,B)||isSubStructure(A->right,B);
    }
};

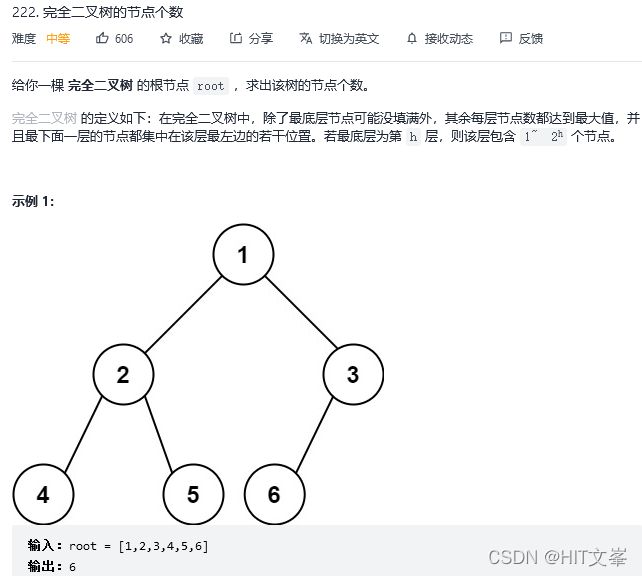
29. 完全二叉树的节点个数

解法1：深度优先搜索（递归）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
       if(root==nullptr) return 0;
       return 1+countNodes(root->left)+countNodes(root->right);//后序遍历
    }
};
/*int leftNum = getNodesNum(cur->left);      // 左
  int rightNum = getNodesNum(cur->right);    // 右
  int treeNum = leftNum + rightNum + 1;      // 中
  return treeNum; */

• 时间复杂度：O(n)
• 空间复杂度：O(log n)，主要是递归栈占用的空间。

解法2：广度优先搜索（迭代）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * }; */
class Solution {
public:
    int countNodes(TreeNode* root) {
      queue que;
      if(root!=nullptr) que.push(root);
      int ans=0;
      while(!que.empty()){
          int size=que.size();
          for(int i=0;ileft) que.push(node->left);
              if(node->right) que.push(node->right);
          }
      }
      return ans;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(n)

 解法3：完全二叉树的特性

思路：完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。

对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {          //递归到某一深度一定会有左孩子或者右孩子为满二叉树，利用满二叉树的特性:节点数= 2^树深度 - 1 
public:
    int countNodes(TreeNode* root) {
        if(root==nullptr) return 0;
        int leftHeight=0,rightHeight=0; // 这里初始为0是有目的的，为了下面求指数方便
        TreeNode *left=root->left;
        TreeNode *right=root->right;

        //求左子树深度
        while(left){
            left=left->left;
            leftHeight++;
        }
        //求右子树深度
        while(right){
            right=right->right;
            rightHeight++;
        }
        if(leftHeight==rightHeight){   //找到满二叉树
            return (2<left)+countNodes(root->right);
    }
};

• 时间复杂度：O(logn * logn)
• 空间复杂度：O(logn)

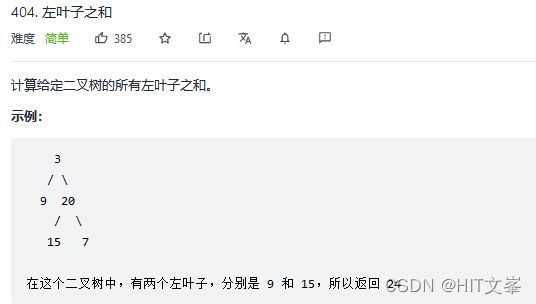
30.左叶子之和

 

解法1：深度优先搜索（递归）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {    //递归      左子树的左叶子+右子树的左叶子
public:        //后序遍历  左  右   中
    //1、确定递归函数的参数和返回值
    int sumOfLeftLeaves(TreeNode* root) {
        //2、确定终止条件
        if(root==nullptr) return 0;
        //3、确定单层递归的逻辑
        int leftSum=sumOfLeftLeaves(root->left);    //左
        int rightSum=sumOfLeftLeaves(root->right);  //右
        int midSum=0;                               //中
        if(root->left!=nullptr && root->left->left==nullptr && root->left->right==nullptr){//左叶子判断条件
            midSum=root->left->val;
        }  
        return leftSum+rightSum+midSum;
    }
};
/*int midSum=0;       简化                     
  if(root->left!=nullptr && root->left->left==nullptr && root->left->right==nullptr){//左叶子判断条件
        midSum=root->left->val;
  }  
  return sumOfLeftLeaves(root->left)+sumOfLeftLeaves(root->right)+midSum; */

• 时间复杂度：O(n)，其中 n 是二叉树中的节点个数。
• 空间复杂度：O(n)，其中 n 是二叉树中的节点个数。空间复杂度与深度优先搜索使用的栈的最大深度相关。最坏的情况下，树呈现链式结构，深度为 O(n)，对应的空间复杂度也为 O(n)。

 解法2：广度优先搜索（迭代）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution { 
public:        //前序遍历   中  左  右
    int sumOfLeftLeaves(TreeNode* root) {
      if(root==nullptr) return 0;
      queue que;
      que.push(root);
      int sum=0;
      while(!que.empty()){
          int size=que.size();
          for(int i=0;ileft!=nullptr && node->left->left==nullptr && node->left->right==nullptr)   //左叶子判断条件
              sum+=node->left->val;             
              if(node->left)  que.push(node->left);
              if(node->right) que.push(node->right);
          }
      }
      return sum;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树中的节点个数。
• 空间复杂度：O(n)，空间复杂度与广度优先搜索使用的队列需要的容量相关，为 O(n)。

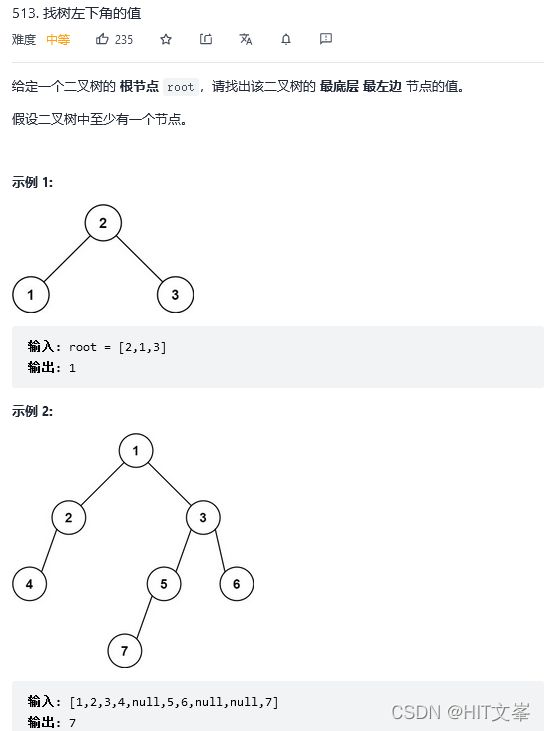
31.找树左下角的值

 

 解法1：广度优先搜索（层序遍历）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
      if(root==nullptr) return 0;
      queue que;
      que.push(root);
      int ans;
      while(!que.empty()){
          int size=que.size();
          for(int i=0;ival;     //每层最左侧的元素
              
              if(node->left) que.push(node->left);
              if(node->right) que.push(node->right);
          }
      }
      return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树中的节点个数。
• 空间复杂度：O(n)，空间复杂度与广度优先搜索使用的队列需要的容量相关，为 O(n)。

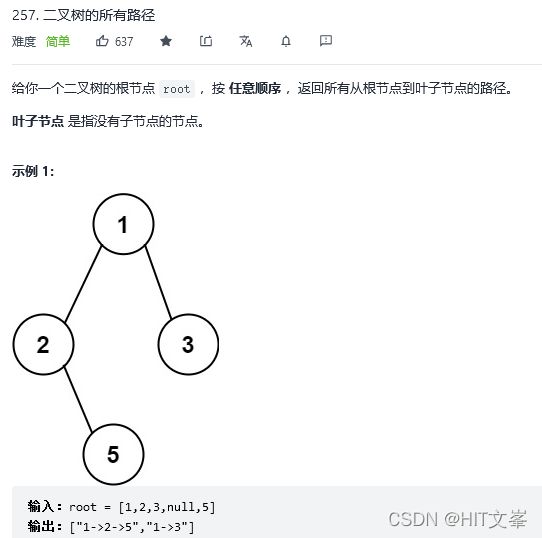
32.二叉树的所有路径

 

解法1：递归+回溯

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {
private:
    //要传入根节点、记录每一条路径的path、和存放结果集的ans，这里递归不需要返回值
    void Traversal(TreeNode *node,vector &path, vector &ans){
        path.push_back(node->val);     //因为是前序遍历，需要先处理中间节点，中间节点就是我们要记录路径上的节点，先放进path中
        //然后是递归和回溯的过程
        if(node->left==nullptr && node->right==nullptr){  //终止处理逻辑
            string sPath;
            for(int i=0;ileft){
            Traversal(node->left,path,ans);
            path.pop_back();       //回溯
        }
        if(node->right){
            Traversal(node->right,path,ans);
            path.pop_back();       //回溯
        }
    }
public:
    vector binaryTreePaths(TreeNode* root) {
        vector ans;
        vector path;
        if(root==nullptr) return ans;
        Traversal(root,path,ans);
        return ans;
    }
};

//简化
class Solution {
private:
    //string path，每次都是复制赋值，不用使用引用，否则就无法做到回溯的效果
    void Paths(TreeNode* root, string path, vector& ans) {
        if (root != nullptr) {
            path += to_string(root->val);        //中
            if (root->left == nullptr && root->right == nullptr) {  // 当前节点是叶子节点
                ans.push_back(path);                              // 把路径加入到答案中
            } else {
                path += "->";  // 当前节点不是叶子节点，继续递归遍历（隐藏了回溯）
                Paths(root->left, path, ans);    //左
                Paths(root->right, path, ans);   //右
            }
        }
    }
public:
    vector binaryTreePaths(TreeNode* root) {
        vector ans;
        Paths(root, "", ans);
        return ans;
    }
};

• 时间复杂度：O(n^2)，其中 n 是二叉树中的节点个数。在深度优先搜索中每个节点会被访问一次且只会被访问一次，每一次会对 path 变量进行拷贝构造，时间代价为 O(n)，故时间复杂度为 O(n^2)。
• 空间复杂度：O(n^2)，其中 n 是二叉树中的节点个数。我们需要考虑递归调用的栈空间。在最坏情况下，当二叉树中每个节点只有一个孩子节点时，即整棵二叉树呈一个链状，此时递归的层数为 n，此时每一层的 path 变量的空间代价的总和为O(n^2)， 空间复杂度为 O(n^2)。最好情况下，当二叉树为平衡二叉树时，它的高度为 log⁡n，此时空间复杂度为 O((log⁡n)^2)。 

递归函数是否需要返回值

• 如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。
• 如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。
• 如果需要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（注意返回的类型）

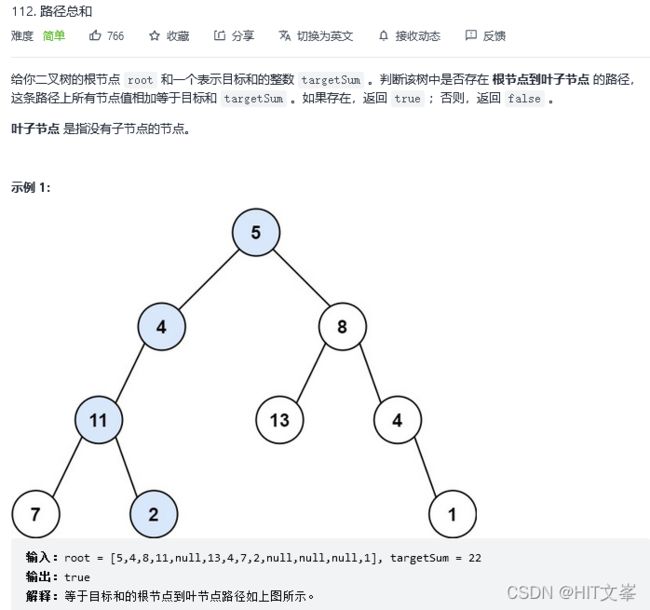
33.路径总和

解法1：深度优先搜索（递归）

思路：不要去累加然后判断是否等于目标和，那么代码比较麻烦。可以用递减，让计数器count初始为目标和，然后每次减去遍历路径节点上的数值。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution { 
public:
     //1、确定递归函数的参数和返回类型
    bool traversal(TreeNode *node, int count){
        //2、递归终止条件代码
        if(node->left==nullptr && node->right==nullptr && count==0) return true;
        //3、确定单层递归的逻辑
        if(node->left){// 左（空节点不遍历）
            count-=node->left->val;   //递归，处理节点
            if(traversal(node->left,count)) return true;
            count+=node->left->val;   //回溯，撤销处理结果
        }
        if(node->right){// 右（空节点不遍历）
            if(traversal(node->right,count - node->right->val))  return true;   //隐藏回溯的逻辑
            //count-=node->right->val;
            //if(traversal(node->right,count)) return true;
            //count+=node->right->val;     
        }
        return false;
    }
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root==nullptr) return false;
        return traversal(root,targetSum - root->val);
    }
};

class Solution {  //简化
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
      if(root==nullptr) return false;
      if(root->left==nullptr && root->right==nullptr && targetSum==root->val) return true;
      return hasPathSum(root->left,targetSum-root->val) || hasPathSum(root->right,targetSum-root->val);
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树中的节点个数。
• 空间复杂度：O(h)，其中 h 是树的高度。空间复杂度主要取决于递归时栈空间的开销，最坏情况下，树呈现链状，空间复杂度为 O(n)。平均情况下树的高度与节点数的对数正相关，空间复杂度为 O(log⁡n)。

解法2：广度优先搜索（迭代）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
       if(root==nullptr)  return false;
       // 此时栈里要放的是pair<节点指针，路径数值>
       stack> stk;
       stk.push(pair(root,root->val));

       while(!stk.empty()){
           pair node=stk.top();
           stk.pop();
           if(node.first->left==nullptr && node.first->right==nullptr && targetSum==node.second)  return true;

           //左节点，压进去一个节点的时候，将该节点的路径数值也记录下来
           if(node.first->left)  stk.push(pair(node.first->left,node.second+node.first->left->val));
           if(node.first->right) stk.push(pair(node.first->right,node.second+node.first->right->val));
       }
       return false;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树中的节点个数。
• 空间复杂度：O(n)，其中 n 是二叉树中的节点个数。空间复杂度主要取决于队列的开销，队列中的元素个数不会超过树的节点数。

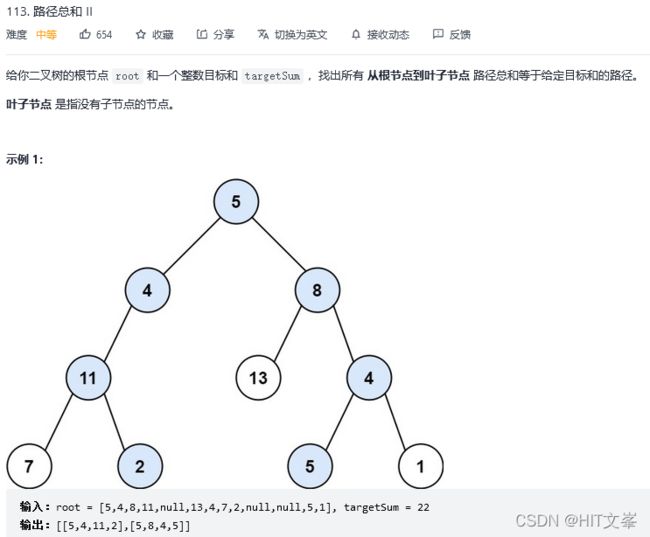
34.路径总和II

解法1：深度优先搜索（递归）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {
private:
     // 递归函数不需要返回值，因为我们要遍历整个树
     void traversal(TreeNode* node,int count){
         if(node->left==nullptr && node->right==nullptr && count==0){//找到叶子节点，且找到目标路径和
            ans.push_back(vec);
            return;
         }

         if(node->left){     //遍历左节点
             vec.push_back(node->left->val);
             count-=node->left->val;
             traversal(node->left,count);   //递归
             count+=node->left->val;        //回溯
             vec.pop_back();                //回溯
         }
         if(node->right){
             vec.push_back(node->right->val);
             traversal(node->right,count-=node->right->val); //隐藏回溯
             vec.pop_back();
         }
         return;
     }
     vector> ans;
     vector vec;
public:
    vector> pathSum(TreeNode* root, int targetSum) {
        //ans.clear();
        //vec.clear();
        if(root==nullptr) return ans;
        vec.push_back(root->val);    //把根节点放入路径
        traversal(root,targetSum-root->val);
        return ans;
    }
};

• 时间复杂度：O(n^2)，其中 n 是二叉树中的节点个数。在最坏情况下，树的上半部分为链状，下半部分为完全二叉树，并且从根节点到每一个叶子节点的路径都符合题目要求。此时，路径的数目为 O(n)，并且每一条路径的节点个数也为 O(n)，因此要将这些路径全部添加进答案中，时间复杂度为 O(n^2)。
• 空间复杂度：O(n)，其中 n 是二叉树中的节点个数。空间复杂度主要取决于栈空间的开销，栈中的元素个数不会超过树的节点数。

35.#二叉树中和为某一值的路径

 解法1：回溯+递归

class Solution {
private:
    void Traversal(TreeNode* node,int count){
        if(node->left==nullptr&&node->right==nullptr&&count==0){
            ans.push_back(path);return;
        }
        if(node->left){
            path.push_back(node->left->val);
            Traversal(node->left,count-node->left->val);
            path.pop_back();
        }
        if(node->right){
            path.push_back(node->right->val);
            Traversal(node->right,count-node->right->val);
            path.pop_back();
        }
        return;
    }
    vector path;
    vector> ans;
public:
    vector> pathSum(TreeNode* root, int target) {
        if(root==nullptr) return ans;
        path.push_back(root->val);
        Traversal(root,target-root->val);
        return ans; 
    }
};

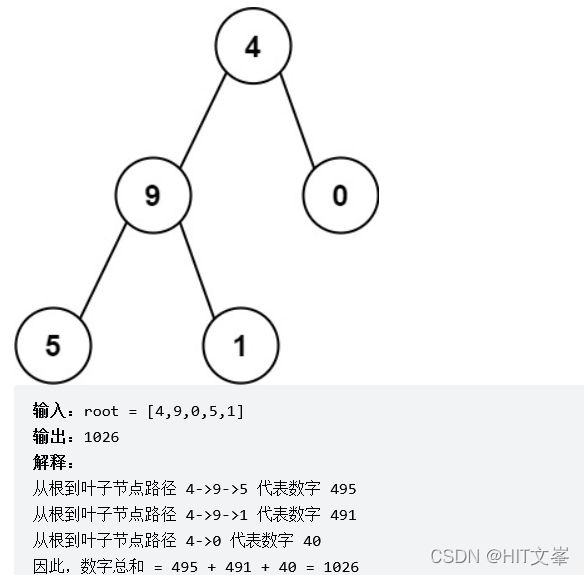
36.求根节点到叶节点数字之和

 

 解法1：深度优先搜索

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {
private:
    //将数组转化为int
    int pathToInt(vector &nums){
        int sum=0;
        for(int i=0;ileft && !node->right){  //终止条件是碰到叶子节点
            ans+=pathToInt(path);
            return;
        }
        if(node->left){// 左 （空节点不遍历）
            path.push_back(node->left->val); // 处理节点
            Traversal(node->left);           //递归
            path.pop_back();                  //回溯
        }
        if(node->right){
            path.push_back(node->right->val);
            Traversal(node->right);
            path.pop_back();
        }
    }
    int ans;
    vector path;
public:
    int sumNumbers(TreeNode* root) {
        if(root==nullptr) return 0;
        path.push_back(root->val);
        Traversal(root);
        return ans;
    }
};

class Solution {
private:
    int Traversal(TreeNode* node,int preSum){
        if(node==nullptr) return 0;
        int sum=preSum*10+node->val;
        if(!node->left && !node->right){  //终止条件是碰到叶子节点
            return sum;
        }else{
            return Traversal(node->left,sum)+Traversal(node->right,sum);
        }
    }
public:
    int sumNumbers(TreeNode* root) {
        return Traversal(root,0);
    }
};

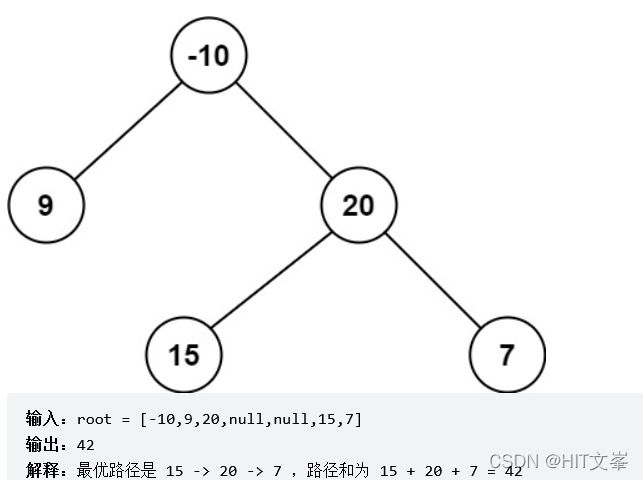
37.*二叉树中的最大路径和

 

 解法1：递归

class Solution {
private:
    //设置一个函数：返回该节点的最大贡献值
    int maxGain(TreeNode *node){
        if(node==nullptr) return 0;
        // 递归计算左右子节点的最大贡献值，并且只有在最大贡献值大于 0 时，才会选取对应子节点
        int left=max(0,maxGain(node->left));
        int right=max(0,maxGain(node->right));
        // 节点的最大路径和：取决于该节点的值与该节点的左右子节点的最大贡献值
        maxSum=max(maxSum,node->val + left + right);
        return node->val+max(left,right);   //最大贡献值：以该节点为根节点+左右子树最大的一个（只能选择一个）
    }
    int maxSum=INT_MIN;
public:
    int maxPathSum(TreeNode* root) {
        maxGain(root);
        return maxSum;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树中的节点个数。对每个节点访问不超过 2 次。
• 空间复杂度：O(n)，其中 n 是二叉树中的节点个数。空间复杂度主要取决于递归调用层数，最大层数等于二叉树的高度，最坏情况下，二叉树的高度等于二叉树中的节点个数。

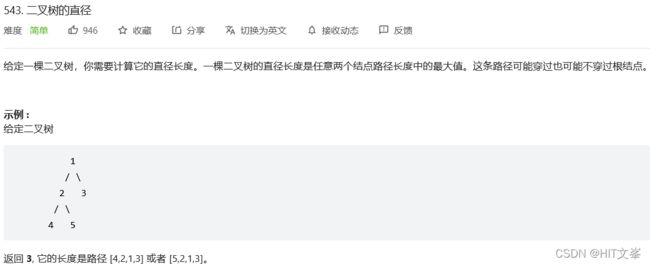
38.*二叉树的直径

 解法1：深度优先搜索

思路：求直径（即求路径长度的最大值）  等效于 求路径经过节点数的最大值 减一

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    int depth(TreeNode* root){
        if(root==nullptr){
            return 0;
        }
        int L=depth(root->left);   // 左儿子为根的子树的深度
        int R=depth(root->right);  // 右儿子为根的子树的深度
        ans=max(ans,L+R+1);        // 计算d_node即L+R+1 并更新ans
        return max(L,R)+1;      // 返回该节点为根的子树的深度
    }
    int ans=1;
public:
    int diameterOfBinaryTree(TreeNode* root) {
        depth(root);
        return ans-1;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树中的节点个数。即遍历一棵二叉树的时间复杂度，每个结点只被访问一次。
• 空间复杂度：O(Height)，其中 Height 为二叉树的高度。

39.从前序与中序遍历序列构造二叉树

 

 解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* Traversal(vector& preorder,vector& inorder){
        if(preorder.size()==0) return nullptr;
        int rootValue=preorder[0];
        TreeNode* root= new TreeNode(rootValue);
        if(preorder.size()==1) return root;
        int index=0;
        for(;index leftInorder(inorder.begin(),inorder.begin()+index);
        vector rightInorder(inorder.begin()+index+1,inorder.end());

        vector leftPreorder(preorder.begin()+1,preorder.begin()+1+leftInorder.size());   //此处  +1  
        vector rightPreorder(preorder.begin()+1+leftInorder.size(),preorder.end());
        root->left=Traversal(leftPreorder,leftInorder);
        root->right=Traversal(rightPreorder,rightInorder);
        return root;
    }
    TreeNode* buildTree(vector& preorder, vector& inorder) {
       if(preorder.size()==0 || inorder.size()==0) return nullptr;
       return Traversal(preorder,inorder);
    }
};

class Solution {
private:
        TreeNode* traversal (vector& inorder, int inorderBegin, int inorderEnd, vector& preorder, int preorderBegin, int preorderEnd) {
        if (preorderBegin == preorderEnd) return NULL;

        int rootValue = preorder[preorderBegin]; // 注意用preorderBegin 不要用0
        TreeNode* root = new TreeNode(rootValue);

        if (preorderEnd - preorderBegin == 1) return root;

        int delimiterIndex;
        for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }
        // 切割中序数组
        // 中序左区间，左闭右开[leftInorderBegin, leftInorderEnd)
        int leftInorderBegin = inorderBegin;
        int leftInorderEnd = delimiterIndex;
        // 中序右区间，左闭右开[rightInorderBegin, rightInorderEnd)
        int rightInorderBegin = delimiterIndex + 1;
        int rightInorderEnd = inorderEnd;

        // 切割前序数组
        // 前序左区间，左闭右开[leftPreorderBegin, leftPreorderEnd)
        int leftPreorderBegin =  preorderBegin + 1;
        int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // 终止位置是起始位置加上中序左区间的大小size
        // 前序右区间, 左闭右开[rightPreorderBegin, rightPreorderEnd)
        int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
        int rightPreorderEnd = preorderEnd;

        root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  preorder, leftPreorderBegin, leftPreorderEnd);
        root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);

        return root;
    }

public:
    TreeNode* buildTree(vector& preorder, vector& inorder) {
        if (inorder.size() == 0 || preorder.size() == 0) return nullptr;
        // 坚持左闭右开的原则
        return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
    }
};

40.从中序与后序遍历序列构造二叉树

解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {
public:
    TreeNode* Traversal(vector &inorder,vector &postorder){
        if(postorder.size()==0) return nullptr;
       
        // 1、后序遍历数组最后一个元素，就是当前的中间节点
        int rootValue=postorder[postorder.size()-1];
        TreeNode *root=new TreeNode(rootValue);     //重点理解
        if(postorder.size()==1) return root;        //叶子节点
        // 2、找到中序遍历的切割点 
        int index=0;    //后面需要用到，必须单独设出
        for(;index < inorder.size();index++){       //此处如果是 int index=0; 就是错误
            if(inorder[index]==rootValue) break;
        }
        // 3、切割中序数组：坚持一致的左闭右开  左闭右开  左闭右开
        vector leftInorder(inorder.begin(),inorder.begin()+index);
        vector rightInorder(inorder.begin()+index+1,inorder.end());
        // 4、切割后序元素：同样坚持左闭右开
        //leftInorder.size()利用前序左数组，因为两个左右数组的个数一定是相等的
        postorder.resize(postorder.size()-1);       //postorder 丢弃已经用过的最后一个元素
        vector leftPostorder(postorder.begin(),postorder.begin()+leftInorder.size());   
        vector rightPostorder(postorder.begin()+leftInorder.size(),postorder.end());
        // 5、递归处理左区间和右区间
        //root->left = traversal(中序左数组, 后序左数组);
        //root->right = traversal(中序右数组, 后序右数组);
        root->left =Traversal(leftInorder,leftPostorder);
        root->right=Traversal(rightInorder,rightPostorder);       
        return root;
    }               
    TreeNode* buildTree(vector& inorder, vector& postorder) {
      if(inorder.size()==0 || postorder.size()==0) return nullptr;
      return Traversal(inorder,postorder);
    }
};

class Solution {    //下表索引  因为原始的代码，每层递归定义了新的vector（就是数组），既耗时又耗空间，
private:
    // 中序区间：[inorderBegin, inorderEnd)，后序区间[postorderBegin, postorderEnd)
    TreeNode* traversal (vector& inorder, int inorderBegin, int inorderEnd, vector& postorder, int postorderBegin, int postorderEnd) {
        if (postorderBegin == postorderEnd) return nullptr;

        int rootValue = postorder[postorderEnd - 1];
        TreeNode* root = new TreeNode(rootValue);
        if (postorderEnd - postorderBegin == 1) return root;
        // 找到中序遍历的切割点
        int index;
        for (index = inorderBegin; index < inorderEnd; index++) {
            if (inorder[index] == rootValue) break;
        }
        // 切割中序数组
        // 左中序区间，左闭右开[leftInorderBegin, leftInorderEnd)
        int leftInorderBegin = inorderBegin;
        int leftInorderEnd = index;
        // 右中序区间，左闭右开[rightInorderBegin, rightInorderEnd)
        int rightInorderBegin = index + 1;
        int rightInorderEnd = inorderEnd;

        // 切割后序数组
        // 左后序区间，左闭右开[leftPostorderBegin, leftPostorderEnd)
        int leftPostorderBegin =  postorderBegin;
        int leftPostorderEnd = postorderBegin + index - inorderBegin; // 终止位置是 需要加上 中序区间的大小size
        // 右后序区间，左闭右开[rightPostorderBegin, rightPostorderEnd)
        int rightPostorderBegin = postorderBegin + (index - inorderBegin);
        int rightPostorderEnd = postorderEnd - 1; // 排除最后一个元素，已经作为节点了

        root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  postorder, leftPostorderBegin, leftPostorderEnd);
        root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);

        return root;
    }
public:
    TreeNode* buildTree(vector& inorder, vector& postorder) {
        if (inorder.size() == 0 || postorder.size() == 0) return NULL;
        // 左闭右开的原则
        return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
    }
};

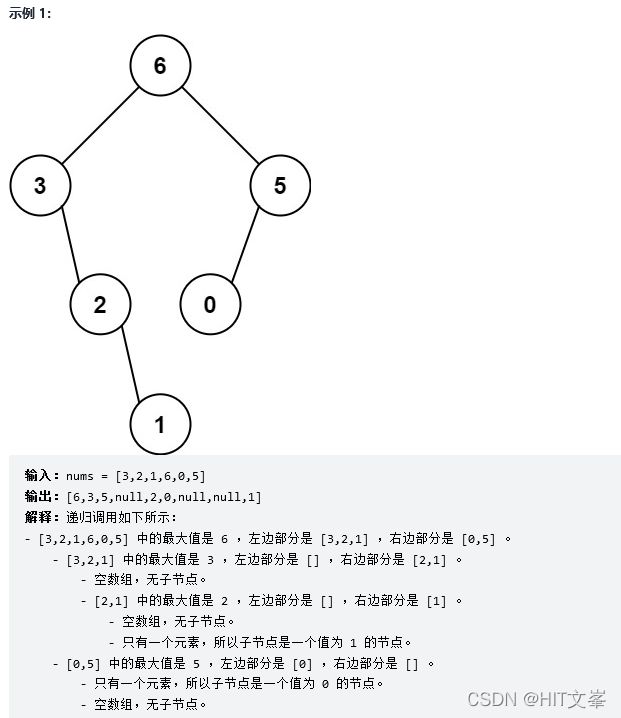
41.最大二叉树

 

 解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector& nums) {
        //当递归遍历的时候，如果传入的数组大小为1，说明遍历到了叶子节点了
        //定义一个新的节点，并把这个数组的数值赋给新的节点，然后返回这个节点。 这表示一个数组大小是1的时候，构造了一个新的节点，并返回。  
        TreeNode *node=new TreeNode(0);
        if(nums.size()==1){
            node->val=nums[0];
            return node;
        }
        //找到数组中最大的值和下标    有能力可考虑哈希
        int maxValue=0,maxValueIndex=0;
        for(int i=0;imaxValue){
                maxValue=nums[i];
                maxValueIndex=i;
            }
        }        
        node->val=maxValue;  //根节点
        //构造左子树
        if(maxValueIndex>0){   //保证左区间至少有一个数值
            vector newVec(nums.begin(),nums.begin()+maxValueIndex);
            node->left=constructMaximumBinaryTree(newVec);
        }
        //构造右子树
        if(maxValueIndex newVec(nums.begin()+maxValueIndex+1,nums.end());
            node->right=constructMaximumBinaryTree(newVec);
        }
        return node;
    }
};

class Solution {    //每次分隔不用定义新的数组，而是通过下表索引直接在原数组上操作
public:
    TreeNode* Traversal(vector &nums,int left,int right){
        if(left>=right) return nullptr;
        //分割点
        int maxValueIndex=left;
        for(int i=left+1;inums[maxValueIndex]) maxValueIndex=i;
        }
        TreeNode* root=new TreeNode(nums[maxValueIndex]);    //重点理解
        //允许空节点进入递归，所以不用在递归的时候加判断节点是否为空
        // 左闭右开：[left, maxValueIndex)
        root->left=Traversal(nums,left,maxValueIndex);
        // 左闭右开：[maxValueIndex + 1, right)
        root->right=Traversal(nums,maxValueIndex+1,right);
        return root;
    }
    TreeNode* constructMaximumBinaryTree(vector& nums) {
       return Traversal(nums,0,nums.size());
    }
};

• 时间复杂度：O(n^2)，其中 n 是二叉树中的节点个数。每次递归寻找根节点时，需要遍历当前索引范围内所有元素找出最大值。一般情况下，每次遍历的复杂度为 O(log⁡n)，总复杂度为 O(nlog⁡n)。最坏的情况下，数组 nums 有序，总的复杂度为O(n^2)。
• 空间复杂度：O(n)，递归调用深度为 n。平均情况下，长度为 n 的数组递归调用深度为O(log⁡n)。

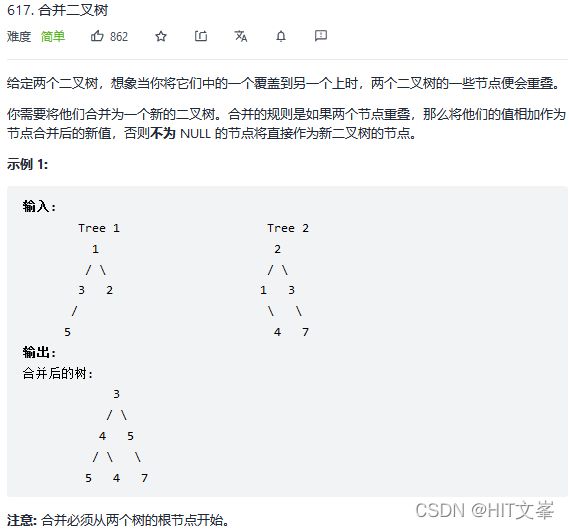
42.合并二叉树

解法1：深度优先搜索（递归）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {   //递归三部曲
public:
    // 1、确定递归函数的参数和返回值：
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        //2、确定终止条件
        if(root1==nullptr) return root2;
        if(root2==nullptr) return root1;
        //3、确定单层递归逻辑
        // 修改了t1的数值和结构
        root1->val+=root2->val;                            //中
        root1->left=mergeTrees(root1->left,root2->left);   //左
        root1->right=mergeTrees(root1->right,root2->right);//右
        return root1;
    }
};

• 时间复杂度：O(min⁡(m,n))，其中 m 和 n 分别是两个二叉树的节点个数。对两个二叉树同时进行深度优先搜索，只有当两个二叉树中的对应节点都不为空时才会对该节点进行显性合并操作，因此被访问到的节点数不会超过较小的二叉树的节点数。
• 空间复杂度：O(min⁡(m,n))，其中 m 和 n 分别是两个二叉树的节点个数。空间复杂度取决于递归调用的层数，递归调用的层数不会超过较小的二叉树的最大高度，最坏情况下，二叉树的高度等于节点数。

解法2：广度优先搜索（迭代）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {     //利用队列 ，模拟层序遍历 ，把两个树的节点同时加入队列
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
      if(root1==nullptr) return root2;
      if(root2==nullptr) return root1;
      queue que;
      que.push(root1);
      que.push(root2);
      while(!que.empty()){
          TreeNode* node1=que.front();  que.pop();
          TreeNode* node2=que.front();  que.pop();
          // 此时两个节点一定不为空，val相加
          node1->val+=node2->val;
          //如果两颗子树的左、右节点都不为空，加入队列
          if(node1->left!=nullptr && node2->left!=nullptr){
              que.push(node1->left);
              que.push(node2->left);
          }
          if(node1->right != nullptr && node2->right!=nullptr){
               que.push(node1->right);
               que.push(node2->right);
          }
          //如果1的左右节点为空，2不为空，就赋值过去
          if(node1->left==nullptr && node2->left!=nullptr)   node1->left=node2->left;
          if(node1->right==nullptr && node2->right!=nullptr)  node1->right=node2->right;
       }
       return root1;
    }
};

• 时间复杂度：O(min⁡(m,n))，其中 m 和 n 分别是两个二叉树的节点个数。对两个二叉树同时进行广度优先搜索，只有当两个二叉树中的对应节点都不为空时才会访问到该节点，因此被访问到的节点数不会超过较小的二叉树的节点数。
• 空间复杂度：O(min⁡(m,n))，其中 m 和 n 分别是两个二叉树的节点个数。空间复杂度取决于队列中的元素个数，队列中的元素个数不会超过较小的二叉树的节点数。

43.验证二叉搜索树

 

解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {       //递归： 中序遍历是递增数组
private:
    void Traversal(TreeNode* root){
        if(root==nullptr) return;     
        Traversal(root->left);
        vec.push_back(root->val);    //将二叉搜索树转化为数组
        Traversal(root->right);
    }
    vector vec;
public:
    bool isValidBST(TreeNode* root) {
        //vec.clear();
        Traversal(root);
        for(int i=1;i

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。在递归调用的时候二叉树的每个节点最多被访问一次，因此时间复杂度为 O(n)。
• 空间复杂度：O(n)，递归函数在递归过程中需要为每一层递归函数分配栈空间，所以这里需要额外的空间且该空间取决于递归的深度，即二叉树的高度。最坏情况下二叉树为一条链，树的高度为 n ，递归最深达到 n 层，故最坏情况下空间复杂度为 O(n)。

解法2：迭代

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) {
       stack stk;
       TreeNode* node=root;
       TreeNode* pre=nullptr;    //哨兵节点，记录前一个元素

       while(node!=nullptr || !stk.empty()){
           if(node!=nullptr){
               stk.push(node);
               node=node->left;
           }else{
               node=stk.top();   //取出栈顶元素
               stk.pop();
               if(pre!=nullptr && pre->val>=node->val)  return false;
               pre=node;        //保持前一个访问节点

               node=node->right;
           }
       }
       return true;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。二叉树的每个节点最多被访问一次，因此时间复杂度为 O(n)。
• 空间复杂度：O(n)，栈最多存储 n 个节点，因此需要额外的 O(n) 的空间。

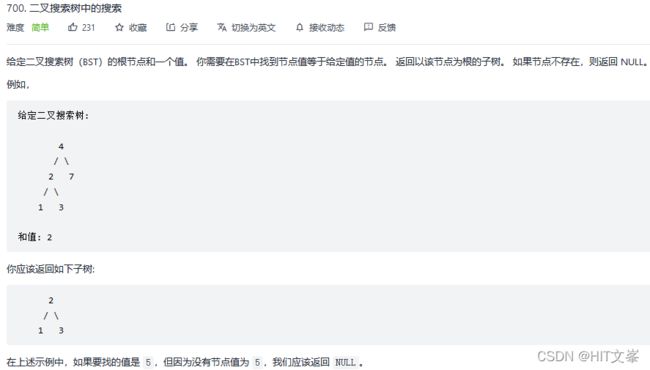
44.二叉搜索树中的搜索

二叉搜索树是一个有序树（中序遍历递增）：

      1、若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

      2、若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

      3、它的左、右子树也分别为二叉搜索树

 解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int target) {
       if(root==nullptr || root->val==target) return root;
       return  searchBST(root->val > target ? root->left : root->right,target);
       //因为搜索到目标节点了，就要立即return，这样才是找到节点就返回（搜索某一条边），如果不加return，就是遍历整棵树了
       //if(root->val > target)  return searchBST(root->left,target);  //搜索左子树 
       //if(root->val < target)  return searchBST(root->right,target); //搜索右子树
       //return root;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉搜索树的节点数。最坏情况下二叉搜索树是一条链，且要找的元素比链末尾的元素值还要小（大），这种情况下我们需要递归 n 次。
• 空间复杂度：O(n)，最坏情况下递归需要 O(n) 的栈空间。

解法2：迭代

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int target) {
      while(root!=nullptr){
          if(target == root->val)  return root;
          root = root->val > target ? root->left : root->right;
          // if(root->val > target)  root=root->left;
          //else if(root->valright;
          //else return root;
      }
      return nullptr;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉搜索树的节点数。最坏情况下二叉搜索树是一条链，且要找的元素比链末尾的元素值还要小（大），这种情况下我们需要迭代 n 次。
• 空间复杂度：O(1)，没有使用额外的空间。

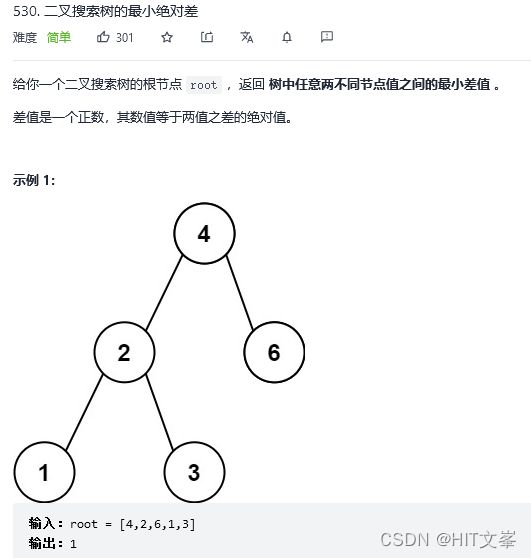
45.二叉搜索树的最小绝对差

解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {
private:
    void traversal(TreeNode* cur) {
        if (cur == nullptr) return;
        traversal(cur->left);   // 左
        if (pre != nullptr){    // 中
            ans = min(ans, cur->val - pre->val);
        }
        pre = cur; // 记录前一个
        traversal(cur->right);  // 右
    }
    int ans = INT_MAX;
    TreeNode  *pre;
public:
    int getMinimumDifference(TreeNode* root) {
        traversal(root);
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。在递归调用的时候二叉树的每个节点最多被访问一次，因此时间复杂度为 O(n)。
• 空间复杂度：O(n)，递归函数的空间复杂度取决于递归的栈深度，而栈深度在二叉搜索树为一条链的情况下会达到 O(n) 级别。

解法2：迭代

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int getMinimumDifference(TreeNode* root) {
      stack stk;
      TreeNode* node=root;
      TreeNode* pre=nullptr;
      int ans=INT_MAX;
      while(node!=nullptr || !stk.empty()){
          if(node!=nullptr) {
              stk.push(node);   //指针访问节点，访问到最底层，将访问的节点放入栈中
              node=node->left;
          }else{
             node=stk.top();
             stk.pop();
             if(pre!=nullptr)  ans=min(ans,node->val - pre->val);
             pre=node;

             node=node->right;
          }
      }
      return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。二叉树的每个节点最多被访问一次，因此时间复杂度为 O(n)。
• 空间复杂度：O(n)，栈最多存储 n 个节点，因此需要额外的 O(n) 的空间。

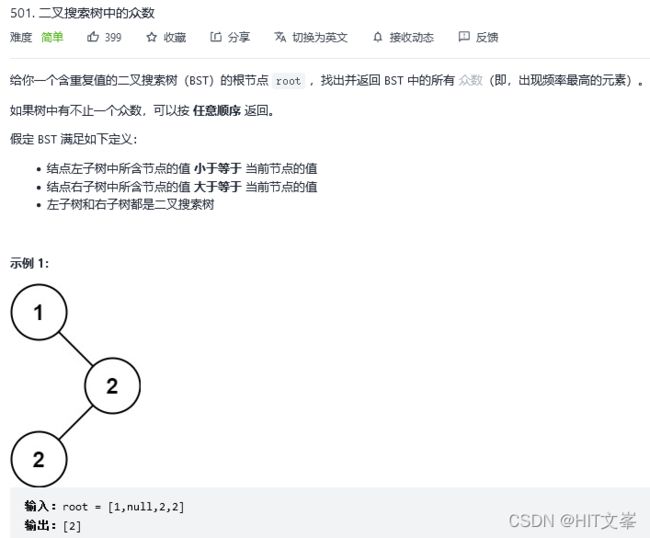
46.二叉搜索树中的众数

解法1：递归（普通二叉树）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {    //如果不是二叉搜索树，而是普通树
public:
    // map    key:元素，value:出现频率
    void searchBST(TreeNode* node,unordered_map& map){
        //前序
        if(node==nullptr) return;
        map[node->val]++;    //统计元素频率
        searchBST(node->left,map);
        searchBST(node->right,map);
        return;
    }
   
    bool static cmp(const pair& a,const pair& b)  {return a.second>b.second;}  // 按照频率从大到小排序

    vector findMode(TreeNode* root) {
        unordered_map map;
        vector ans;
        if(root==nullptr) return ans;
        searchBST(root,map);

        //把map转化数组即vector，再进行排序，当然vector里面放的也是pair类型的数据，第一个int为元素，第二个int为出现频率
        vector>  vec(map.begin(),map.end());
        sort(vec.begin(),vec.end(),cmp);   //给出现的频率排序

        //将出现频率最高的元素放在ans中
        ans.push_back(vec[0].first);
        for(int i=1;i

解法2：递归（二叉搜索树）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxCount,count;
    TreeNode* pre;
    vector ans;
    
    void searchBST(TreeNode* node){
        if(node==nullptr) return;
        searchBST(node->left);   //左
        //中
        if(pre==nullptr){count=1;}
        else if(pre->val==node->val){count++;}   //与前一个节点相同，需要统计频率+1
        else{count=1;}
        pre=node;  //更新上一个节点

        if(count==maxCount){ans.push_back(node->val);}  //和最大值相同，放入数组中
        if(count>maxCount){
            maxCount=count;
            ans.clear();    //更新最大频率后，需要将ans的数组清空，之前的元素全部失效
            ans.push_back(node->val);
        }
        searchBST(node->right);   //右
        return;
    }

    vector findMode(TreeNode* root) {
       count=0;maxCount=0;
       TreeNode* pre=nullptr;  //记录前一个节点
       ans.clear();
       searchBST(root);
       return ans;
    }
};

解法3：迭代

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {    //迭代
public:
    vector findMode(TreeNode* root) {
        int maxCount,count;
        vector ans;
       stack stk;
       TreeNode* node=root;
       TreeNode* pre=nullptr;

       while(node!=nullptr || !stk.empty()){
           if(node!=nullptr){
               stk.push(node);  //指针访问节点，将访问的节点放入栈中
               node=node->left;
           }
           else{
               node=stk.top();stk.pop();
               
               if(pre==nullptr){count=1;}
               else if(pre->val==node->val){count++;}
               else{count=1;}

               if(count==maxCount){ans.push_back(node->val);}
               if(count>maxCount){
                   maxCount=count;
                   ans.clear();
                   ans.push_back(node->val);
               }
               pre=node;
               node=node->right;
           }
       }
       return ans;
    }
};

47.二叉树的最近公共祖先

 

 解法1：递归

 思路： 如果一个节点中左、右子树分别含有p、q,说明找到了公共祖先。如果遇到p或者q，就把q或者p返回，返回值不为空，就说明找到了q或者p。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * }; */
class Solution {   
public:         
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==p || root==q || root==NULL) return root;
        //单层递归逻辑
        TreeNode* left=lowestCommonAncestor(root->left,p,q);
        TreeNode* right=lowestCommonAncestor(root->right,p,q);

        //对left和right进行逻辑处理
        //如果left 和 right都不为空，说明此时root就是最近公共节点。这个比较好理解
        //如果left为空，right不为空，就返回right，说明目标节点是通过right返回的，反之依然
        if(left!=NULL && right!=NULL) return  root;
        if(right==NULL) return  left;
        return right;
        //if(left!=NULL && right==NULL) return  left;
        //if(left==NULL && right!=NULL) return  right;
        //else return NULL;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉树的节点数。在递归调用的时候二叉树的每个节点最多被访问一次，因此时间复杂度为 O(n)。
• 空间复杂度：O(n)，递归函数的空间复杂度取决于递归的栈深度，而栈深度在二叉搜索树为一条链的情况下会达到 O(n) 级别。

48.#二叉树的最近公共祖先

 

 解法1：递归

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==p||root==q||root==NULL) return root;
        TreeNode* L=lowestCommonAncestor(root->left,p,q);
        TreeNode* R=lowestCommonAncestor(root->right,p,q);
        if(L!=NULL && R!=NULL) return root;
        if(L!=NULL){
            return L;
        }else{
            return R;
        }
        
    }
};

49.二叉搜索树的最近公共祖先

解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };*/

class Solution {   //递归:利用二叉搜索树的有序性，根节点的左小右大
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        //if(root==NULL) return root;
        if(root->val > p->val && root->val > q->val){
             return lowestCommonAncestor(root->left,p,q);
         }else if(root->val < p->val && root->val < q->val){
            return lowestCommonAncestor(root->right,p,q);
        } 
        return root;
    }
};

解法2：迭代

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };*/

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        while(root){
            if(root->val > p->val && root->val > q->val) {root=root->left;}
            else if(root->val < p->val && root->val < q->val) {root=root->right;}
            else return root;
        }
        return NULL;
    }
};

• 时间复杂度：O(n)，其中 n 是给定的二叉搜索树中的节点个数。上述代码需要的时间与节点 p 和 q 在树中的深度线性相关，而在最坏的情况下，树呈现链式结构，p 和 q 一个是树的唯一叶子结点，一个是该叶子结点的父节点，此时时间复杂度为 O(n)。
• 空间复杂度：O(1)

50.#二叉搜索树的最近公共祖先

 

解法1：递归

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root->val>p->val && root->val>q->val){
            return lowestCommonAncestor(root->left,p,q); 
        }else if(root->valval && root->valval){
            return lowestCommonAncestor(root->right,p,q);
        }else{
            return root;
        }
    }
};

解法2：迭代

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        while(root){
            if(root->val>p->val && root->val>q->val){
                root=root->left;
            }else if(root->valval && root->valval){
                root=root->right;
            }else{
                return root;
            }
        }
        return NULL;
    }
};

51.二叉搜索树的插入操作

解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {    //二叉搜索树的插入操作，其实是不需要重构搜索树的
public:
    TreeNode* insertIntoBST(TreeNode* root, int target) {
      //终止条件就是找到遍历的节点为null的时候，就是要插入节点的位置了，并把插入的节点返回
      if(root==nullptr){
           return new TreeNode(target);
           //TreeNode* node=new TreeNode(target);
           //return node;
      }
      //通过递归函数返回值完成了新加入节点的父子关系赋值操作，下一层将加入节点返回，本层用root->left或者root->right将其接住。
      if(root->val > target)  root->left = insertIntoBST(root->left,target);
      if(root->val < target)  root->right= insertIntoBST(root->right,target);
      return root;
    }
};

解法2：迭代

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {    //二叉搜索树的插入操作，其实是不需要重构搜索树的
public:
    TreeNode* insertIntoBST(TreeNode* root, int target) {
      //终止条件就是找到遍历的节点为null的时候，就是要插入节点的位置了，并把插入的节点返回
      if(root==nullptr){
          return new TreeNode(target);
          // TreeNode* node=new TreeNode(target);
          // return node;
      }

      TreeNode* node=root;
      TreeNode* parent=nullptr;   // 这个很重要，需要记录上一个节点，否则无法赋值新节点
      while(node!=nullptr){
          parent=node;
          if(node->val > target) node=node->left;
          else node=node->right;
      }

      //下面的迭代目的是把数值插入
      TreeNode* cur=new TreeNode(target);
      if(parent->val > target) parent->left=cur;      // 此时是用parent节点的进行赋值
      else parent->right=cur;
      return root;
    }
};

52.删除二叉搜索树中的节点

 解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
            // 第一种情况：没找到删除的节点，遍历到空节点直接返回了
       if(root==nullptr) return root;
       if(root->val > key) root->left=deleteNode(root->left,key);
       if(root->val < key) root->right=deleteNode(root->right,key);
       if(root->val ==key){
            // 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回nullptr为根节点
            if(root->left==nullptr && root->right==nullptr){
                  delete root;    //释放内存
                  return nullptr;
             }
            // 第三种情况：其左孩子为空，右孩子不为空，删除节点，右孩子补位 ，返回右孩子为根节点
             else if(root->left==nullptr){
                 auto rootNode=root->right;
                 delete root;
                 return rootNode;
             }  
             // 第四种情况：其右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
             else if(root->right==nullptr){
                 auto rootNode=root->left;
                 delete root;
                 return rootNode;
             }
             // 第五种情况：左右孩子节点都不为空，则将 删除节点的左子树 放到 删除节点的右子树的最左面节点 的左孩子 的位置
             // 并返回删除节点右孩子为新的根节点。
             else{
                 // 找右子树最左面的节点
                 TreeNode* node=root->right;       //右子树
                 while(node->left!=nullptr) { node=node->left;}

                 node->left=root->left;            // 把要删除的节点（root）左子树放在node的左孩子的后面

                 //TreeNode* tmp=root;              //为了释放内存做准备
                 root=root->right;                // 返回旧root的右孩子作为新root
                 //delete tmp;
                 return root;
             }
       } 
       return root;
    }
};

53.修剪二叉搜索树

 解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(root==nullptr) return nullptr;
        // 寻找符合区间[low, high]的节点
        if(root->val < low) return trimBST(root->right,low,high);
        if(root->val > high) return trimBST(root->left,low,high);
      
        root->left=trimBST(root->left,low,high);   // root->left接入符合条件的左孩子（将下一层处理完左子树的结果赋给root->left）
        root->right=trimBST(root->right,low,high); // root->right接入符合条件的右孩子
        return root;
    }
};
//if(root->val < low) return trimBST(root->right,low,high);
//root->left=trimBST(root->left,low,high);
//两步组合相当于 将不符合条件的节点删除

• 时间复杂度：O(n)，其中 n 是给定的二叉搜索树中的节点个数。我们最多访问每个节点一次。
• 空间复杂度：O(n)，在最糟糕的情况下，我们递归调用的栈可能与节点数一样大。

解法2：迭代

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
       if(!root)   return nullptr;
       //  1、 处理头结点，让root移动到[L, R] 范围内，注意是左闭右闭
       while(root!=nullptr && (root->valval>high)){
           if(root->val < low) {root=root->right;}
           else root=root->left;
       }

       TreeNode* node=root;
       // 2、此时root已经在[L, R] 范围内，处理左孩子元素小于L的情况
       while(node!=nullptr){
           while(node->left && node->left->val < low){
               node->left=node->left->right;
           }
           node=node->left;
       }

       node=root;
       // 此时root已经在[L, R] 范围内，处理右孩子大于R的情况
       while(node!=nullptr){
           while(node->right && node->right->val > high){
               node->right=node->right->left;
           }
           node=node->right;
       }
       return root;
    }
}

54.将有序数组转换为二叉搜索树

 

解法1：递归

思路：默认以数组的中间位置元素作为根节点，这样会自动的生成平衡二叉树。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {     //全程坚持左闭右闭区间      中序遍历
public:
    TreeNode* Traversal(vector& nums,int left,int right){
        if(left>right) return nullptr;

        int mid=left+(right-left)/2;    
        TreeNode* root=new TreeNode(nums[mid]);   //取了中间位置，就开始以中间位置的元素构造节点

        root->left=Traversal(nums,left,mid-1);    //构建左子树
        root->right=Traversal(nums,mid+1,right);
        return root;
    }
    TreeNode* sortedArrayToBST(vector& nums) {
      return Traversal(nums,0,nums.size()-1);
    }
};

• 时间复杂度：O(n)，其中 n 是数组的长度。每个数字只访问一次。
• 空间复杂度：O(log⁡n)，其中 n 是数组的长度。空间复杂度不考虑返回值，因此空间复杂度主要取决于递归栈的深度，递归栈的深度是 O(log⁡n)。

55.将二叉搜索树变平衡

 

 解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    //将二叉搜索树转化为有序数组：中序遍历
    void traversal(TreeNode* node){
        if(node==nullptr) return;
        traversal(node->left);
        vec.push_back(node->val);
        traversal(node->right);
    }
    //将有序数组转化为平衡二叉树
    TreeNode* getTree(vector& nums,int left,int right){
        if(left>right) return nullptr;  //终止条件
        int mid=(right-left)/2+left; 
        TreeNode* root=new TreeNode(nums[mid]);
        root->left=getTree(nums,left,mid-1);
        root->right=getTree(nums,mid+1,right);
        return root;
    }
    vector vec;
public:
    TreeNode* balanceBST(TreeNode* root) {
        traversal(root);
        return getTree(vec,0,vec.size()-1);
    }
};

• 时间复杂度：O(n)，其中 n 是数组的长度。每个数字只访问一次。
• 空间复杂度：O(n)，使用了一个数组作为辅助空间，存放中序遍历后的有序序列，故渐进空间复杂度为 O(n)。

56.把二叉搜索树转换为累加树

 

解法1：反中序遍历+递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {   //递归： 反中序遍历（右中左）  依次相加
private:
     void Traversal(TreeNode* root){  //不需要有返回值
        if(root==nullptr) return;
        Traversal(root->right);
        root->val += pre;
        pre=root->val;
        Traversal(root->left);
     }
     int pre=0;  //用于记录root前的数值
public:
    TreeNode* convertBST(TreeNode* root) {        
        Traversal(root);
        return root;
    }
};

class Solution {
private:
    int sum = 0;
public:
    TreeNode* convertBST(TreeNode* root) {
        if (root != nullptr) {
            convertBST(root->right);
            sum += root->val;
            root->val = sum;
            convertBST(root->left);
        }
        return root;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉搜索树的节点数。每一个节点恰好被遍历一次。
• 空间复杂度：O(n)，为递归过程中栈的开销，平均情况下为 O(log⁡n)，最坏情况下树呈现链状，为 O(n)。

解法2：反中序遍历+迭代

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * }; */
class Solution {   
public:
    TreeNode* convertBST(TreeNode* root) {
        stack stk;
        if(root!=nullptr) stk.push(root);
        int sum=0;
        while(!stk.empty()){
            TreeNode *node=stk.top();
            if(node!=nullptr){
                stk.pop();
                if(node->left) stk.push(node->left);    //左
                stk.push(node);                         //中
                stk.push(nullptr);
                if(node->right) stk.push(node->right);  //右
            }else{
                stk.pop();
                node=stk.top();   
                stk.pop();

                sum+=node->val;
                node->val=sum; 
            }
        }
        return root;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉搜索树的节点数。每一个节点恰好被遍历一次。
• 空间复杂度：O(n)

57.#二叉搜索树的第k大节点

 解法1：反中序遍历+递归

class Solution {
private:
    void Traversal(TreeNode* root, int& k){ //必须加 & 不然错误
        if(root==NULL) return;
        Traversal(root->right,k);
        if(--k==0) ans=root->val;
        Traversal(root->left,k);
    }
    int ans;
public:
    int kthLargest(TreeNode* root, int k) {
        Traversal(root,k);
        return ans;       
    }
};

58.*二叉树展开为链表

解法1：递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };*/
class Solution {   //递归实现前序遍历
private:
    void Traversal(TreeNode* root,vector &vec){
        if(root!=nullptr){
            vec.push_back(root);
            Traversal(root->left,vec);
            Traversal(root->right,vec);
        }
    }
public:
    void flatten(TreeNode* root) {
        vector vec;
        Traversal(root,vec);
        for(int i=1;ileft=nullptr;
            prev->right=cur;
        }
    }
};

• 时间复杂度：O(n)，其中 n 是二叉搜索树的节点数。前序遍历的时间复杂度是 O(n)，前序遍历之后，需要对每个节点更新左右子节点的信息，时间复杂度也是 O(n)。
• 空间复杂度：O(n)，其中 n 是二叉搜索树的节点数。空间复杂度取决于栈（递归调用栈或者迭代中显性使用的栈）和存储前序遍历结果的列表的大小，栈内的元素个数不会超过 n，前序遍历列表中的元素个数是 n。

解法2：寻找前驱节点

 思路：如果一个节点的左子节点为空，则该节点不需要进行展开操作。如果一个节点的左子节点不为空，则该节点的左子树中的最后一个节点被访问之后，该节点的右子节点被访问。该节点的左子树中最后一个被访问的节点是左子树中的最右边的节点，也是该节点的前驱节点。因此，问题转化成寻找当前节点的前驱节点。

class Solution {
public:
    void flatten(TreeNode* root) {
        TreeNode *cur=root;
        while(cur!=nullptr){
            //如果当前节点的左子节点不为空，则需要找到左子树中最下方最右边的节点，作为当前节点的右子节点的根节点
            if(cur->left!=nullptr){
                TreeNode *next=cur->left;
                TreeNode *pre=next;
                while(pre->right!=nullptr){   //寻找左子树中最下方最右边的节点（前驱节点）
                    pre=pre->right;
                }
                //作为当前节点的右子节点的根节点
                pre->right=cur->right;
                //为下一次循环做准备
                cur->left=nullptr;
                cur->right=next;
            }
            cur=cur->right;    //如果当前节点的左子节点为空，则该节点不需要进行展开操作。
        }
    }
};

• 时间复杂度：O(n)，其中 n 是二叉搜索树的节点数。展开为单链表的过程中，需要对每个节点访问一次，在寻找前驱节点的过程中，每个节点最多被额外访问一次。
• 空间复杂度：O(1)。

59.#二叉搜索树与双向链表

 

 

 

 解法1：递归

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node() {}
    Node(int _val) {
        val = _val;
        left = NULL;
        right = NULL;
    }
    Node(int _val, Node* _left, Node* _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};*/
class Solution {
private:
    void Traversal(Node* node){
        if(node==NULL) return;
        Traversal(node->left);
        if(tail!=NULL){//tail相当于前驱节点，node相当于当前节点
            tail->right=node;
            node->left=tail;
        }else{//代表正在访问链表头节点，记为 head ；
            head=node;
        }
        tail=node;  //更新 tail = node ，即节点 node 是后继节点的 tail 
        Traversal(node->right);
    }
    Node *head,*tail;
public:
    Node* treeToDoublyList(Node* root) {
        if(root==NULL) return NULL;
        Traversal(root); //中序遍历
        head->left=tail;
        tail->right=head;
        return head;
    }
};

• 时间复杂度：O(n)，其中 n 是二叉搜索树的节点数。中序遍历需要访问所有节点。
• 空间复杂度：O(n)，最差情况下，即树退化为链表时，递归深度达到 n，系统使用 O(n) 栈空间。

60.*二叉树的序列化与反序列化

 

 解法1：深度优先搜索

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * }; */
class Codec {   //深度优先搜索：前序遍历
private:
    void rserialize(TreeNode *root,string &str){
        if(root==NULL){
            str+="null,";
        }else{
            str+=to_string(root->val)+",";  //to_string 将数字转化为字符类型
            rserialize(root->left,str);
            rserialize(root->right,str);
        }
    }

    TreeNode *rdeserialize(list& data){
        if(data.front()=="null"){  //获取字符串第一个字符
            data.erase(data.begin());    //删除第一个元素：erase()返回值是删除元素的下一个迭代位置
            return NULL;                 //删除最后一个元素：data.pop_back();
        }
        //不为空：先解析这棵树的左子树，再解析它的右子树
        TreeNode *root=new TreeNode(stoi(data.front()));  //stoi()的参数是const string，作用是把数字字符串转换成int输出
        data.erase(data.begin());
        root->left=rdeserialize(data);
        root->right=rdeserialize(data);
        return root;
    }
public:
    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        string str;
        rserialize(root,str);
        return str;
    }

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        list dataList;
        string str;
        for(auto &ch:data){
            //首先我们需要根据 , 把原先的序列分割开来得到先序遍历的元素列表，然后从左向右遍历这个序列
            if(ch==','){
                dataList.push_back(str);
                str.clear();
            }else{
                str.push_back(ch);
            }
        }  
        if(!str.empty()){
            dataList.push_back(str);
            str.clear();
        }
        return rdeserialize(dataList);
    }
};

// Your Codec object will be instantiated and called as such:
// Codec ser, deser;
// TreeNode* ans = deser.deserialize(ser.serialize(root));

• 时间复杂度：O(n)，其中 n 是节点数，即树的大小。在序列化和反序列化函数中，我们只访问每个节点一次。
• 空间复杂度：O(n)，在序列化和反序列化函数中，我们递归会使用栈空间。

61.#序列化二叉树

 

 解法1：深度优先搜索

class Codec {   //深度优先搜索：前序遍历
private:
    void rserialize(TreeNode *root,string &str){
        if(root==NULL){
            str+="null,";
        }else{
            str+=to_string(root->val)+",";  //to_string 将数字转化为字符类型
            rserialize(root->left,str);
            rserialize(root->right,str);
        }
    }

    TreeNode *rdeserialize(list& data){
        if(data.front()=="null"){  //获取字符串第一个字符
            data.erase(data.begin());    //删除第一个元素：erase()返回值是删除元素的下一个迭代位置
            return NULL;                 //删除最后一个元素：data.pop_back();
        }
        //不为空：先解析这棵树的左子树，再解析它的右子树
        TreeNode *root=new TreeNode(stoi(data.front()));  //stoi()的参数是const string，作用是把数字字符串转换成int输出
        data.erase(data.begin());
        root->left=rdeserialize(data);
        root->right=rdeserialize(data);
        return root;
    }
public:
    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        string str;
        rserialize(root,str);
        return str;
    }

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        list dataList;
        string str;
        for(auto &ch:data){
            //首先我们需要根据 , 把原先的序列分割开来得到先序遍历的元素列表，然后从左向右遍历这个序列
            if(ch==','){
                dataList.push_back(str);
                str.clear();
            }else{
                str.push_back(ch);
            }
        }  
        if(!str.empty()){
            dataList.push_back(str);
            str.clear();
        }
        return rdeserialize(dataList);
    }
};

// Your Codec object will be instantiated and called as such:
// Codec ser, deser;
// TreeNode* ans = deser.deserialize(ser.serialize(root));

题型十四：回溯

0.回溯的基础知识

 （1） 回溯是递归的副产品，只要有递归就会有回溯。回溯的本质是穷举，其实就是暴力查找，并不是什么高效的算法，最多是加上剪枝进行优化。

（2）回溯能解决的几类问题：

• 组合问题：n个数里面按一定规则找出k个数的集合
• 切割问题：一个字符串按一定规则有几种切割方式
• 子集问题：一个n个数的集合里有多少符合条件的子集
• 排列问题：n个数按一定规则全排列，有几种排列方式
• 棋盘问题：n皇后，解数独等等

（3）回溯三步曲

 所有回溯法的问题都可以抽象为树形结构：回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度构成的树的深度。for循环可以理解为横向遍历，backTracking 就是纵向遍历。

void backTracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }
    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backTracking(路径，选择列表);   // 递归
        回溯，撤销处理结果 
    }
}

（4）  如果是一个集合来求组合的话，就需要startIndex，
           如果是多个集合取组合，各个集合之间相互不影响，那么就不用startIndex.

1.组合

解法1：回溯

class Solution {
private:
    void backTracking(int n,int k,int startIndex){//每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围，就是要靠startIndex。
        if(path.size()==k){
            ans.push_back(path);     //存放结果;
            return;
        }
        for(int i=startIndex;i<=n;++i){ // 控制树的横向遍历
            path.push_back(i);          // 处理节点 
            backTracking(n,k,i+1);      // 递归：控制树的纵向遍历，注意下一层搜索要从i+1开始
            path.pop_back();            // 回溯，撤销处理的节点
        }
    }
    vector path;
    vector> ans;
public:
    vector> combine(int n, int k) {
       //path.clear();
       //ans.clear(); 
       backTracking(n,k,1);
       return ans;
    }
};

解法2：回溯（优化）

思路：如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数，那么就没有必要搜索了。

//已经选择的元素个数：path.size();
//还需要的元素个数为: k - path.size();
//在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++)  //注意+1，保持左闭

2.*电话号码的字母组合

 解法1：回溯+哈希

class Solution {
private:
    //首先使用哈希表存储每个数字对应的所有可能的字母，然后进行回溯操作
    unordered_map phoneMap{
            {'2', "abc"},
            {'3', "def"},
            {'4', "ghi"},
            {'5', "jkl"},
            {'6', "mno"},
            {'7', "pqrs"},
            {'8', "tuv"},
            {'9', "wxyz"}
        };

    //index是记录遍历第几个数字了，就是用来遍历digits（数字字符串），同时index也表示树的深度。
    void backTracking(const string& digits,int index){
        if(digits.size()==index){
            ans.push_back(s);
            return;
        }
  
        //取出哈希表中数字所对应的字符集
        char digit=digits[index];
        string letters=phoneMap.at(digit);

        for(int i=0;i ans;
    string s;
public:
    vector letterCombinations(string digits) {
       //s.clear();
       //ans.clear();
       if(digits.empty()){return ans;}
       backTracking(digits,0);
       return ans;
    }
};

• 时间复杂度：O(3^m × 4^n)，其中 m 是输入中对应 3 个字母的数字个数，n 是输入中对应 4 个字母的数字个数，m+n 是输入数字的总个数。当输入包含 m 个对应 3 个字母的数字和 n 个对应 4 个字母的数字时，不同的字母组合一共有 3^m × 4^n 种，需要遍历每一种字母组合。
• 空间复杂度：O(m+n)，除了返回值以外，空间复杂度主要取决于哈希表以及回溯过程中的递归调用层数，哈希表的大小与输入无关，可以看成常数，递归调用层数最大为 m+n。

3.*组合总和

  解法1：回溯

class Solution {
private:
    void backTracking(vector& candidates,int target,int sum,int startIndex){
        if(sum>target){return;}
        if(sum==target){
            ans.push_back(path);
            return;
        }
        //本题元素是可以重复选择的
        for(int i=startIndex;ipath;
    vector> ans;

public:
    vector> combinationSum(vector& candidates, int target) {
      //path.clear();
      //ans.clear();
      backTracking(candidates,target,0,0);
      return ans;
    }
};

• 时间复杂度：O(s)，其中 s 是所有可行解的长度之和。
• 空间复杂度：O(target)，除答案数组外，空间复杂度取决于递归的栈深度，在最差情况下需要递归 O(target) 层。

解法2：回溯（优化）

class Solution {
private:
    void backTracking(vector& candidates,int target,int sum,int startIndex){
        //if(sum>target){return;}
        if(sum==target){
            ans.push_back(path);
            return;
        }
        //本题元素是可以重复选择的
        // 如果 sum + candidates[i] > target 就终止遍历（优化，需要排序）
        for(int i=startIndex;ipath;
    vector> ans;

public:
    vector> combinationSum(vector& candidates, int target) {;
      sort(candidates.begin(),candidates.end());   //需要排序
      backTracking(candidates,target,0,0);
      return ans;
    }
};

4.组合总和II

 解法1：回溯（startIndex去重）

class Solution {
private:
    //去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。
    void backTracking(vector& candidates,int target,int sum,int startIndex){
       if(sum==target){
           ans.push_back(path);
           return;
       }
       //单层搜索的逻辑
       for(int i=startIndex;istartIndex
           if(i>startIndex && candidates[i]==candidates[i-1]){continue;}

           sum+=candidates[i];
           path.push_back(candidates[i]);          
           backTracking(candidates,target,sum,i+1);// 和39.组合总和区别:这里是i+1，每个数字在每个组合中只能使用一次       
           sum-=candidates[i];
           path.pop_back();      
       }
    }
    vector path;
    vector> ans;
public:
    vector> combinationSum2(vector& candidates, int target) {
      //path.clear();
      //ans.clear();
      sort(candidates.begin(),candidates.end());  // 首先把给candidates排序，让其相同的元素都挨在一起。
      backTracking(candidates,target,0,0);
      return ans;
    }
};

• 时间复杂度：O( n × 2^n)，其中 n 是数组 candidates 的长度。在递归时，每个位置可以选或不选，如果数组中所有数的和不超过 target，那么 2^n 种组合都会被枚举到；每得到一个满足要求的组合，需要 O(n) 的时间将其放入答案中，因此我们将 O(2^n) 与 O(n) 相乘，即可估算出一个宽松的时间复杂度上界。由于 O( n × 2^n) 在渐进意义下大于排序的时间复杂度 O(nlog⁡n)，因此后者可以忽略不计。
• 空间复杂度：O(n)，空间复杂度取决于递归的栈深度，在最差情况下需要递归 O(n) 层。

 解法2：回溯（used去重）

class Solution {
private:
    //bool型数组used，用来记录同一树枝上的元素是否使用过，担负去重的重任
    //去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。
    void backTracking(vector& candidates,int target,int sum,int startIndex,vector& used){
       if(sum==target){
           ans.push_back(path);
           return;
       }
       //单层搜索的逻辑
       for(int i=startIndex;i0 && candidates[i]==candidates[i-1] && used[i-1]==false){continue;}

           sum+=candidates[i];
           path.push_back(candidates[i]);
           used[i]=true;
           backTracking(candidates,target,sum,i+1,used);// 和39.组合总和区别:这里是i+1，每个数字在每个组合中只能使用一次
           used[i]=false;
           sum-=candidates[i];
           path.pop_back();      
       }
    }
    vector path;
    vector> ans;
public:
    vector> combinationSum2(vector& candidates, int target) {
      vector used(candidates.size(),false);   
      sort(candidates.begin(),candidates.end());  // 首先把给candidates排序，让其相同的元素都挨在一起。
      backTracking(candidates,target,0,0,used);
      return ans;
    }
};

5.组合总和III

 

解法1：回溯

class Solution {
private:
    void backTracking(int k,int n,int sum,int startIndex){
        if(path.size()==k){  //数量要求体现在这里
            // sum：已经收集的元素的总和，也就是path里元素的总和。
            if(sum==n) ans.push_back(path);
            return;       // 如果path.size() == k 但sum != targetSum 直接返回
        }
        //处理过程 和 回溯过程是一一对应的，处理有加，回溯就要有减
        for(int i=startIndex;i<=9;++i){
            sum+=i;
            path.push_back(i);
            backTracking(k,n,sum,i+1);  // i+1表示不能重复
            sum-=i;
            path.pop_back();
        }
    }
    vectorpath;
    vector> ans;
public:
    vector> combinationSum3(int k, int n) {
      //path.clear();
      //ans.clear();
      backTracking(k,n,0,1);
      return ans;
    }
};

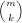• 时间复杂度：O(×k)，其中 m 为集合的大小，本题中 m 固定为 9。一共有 个组合，每次判断需要的时间代价是 O(k)。
• 空间复杂度：O(m)，path 数组的空间代价是 O(k)，递归栈空间的代价是 O(m)，故空间复杂度为 O(m+k)=O(m)。

解法2：回溯（优化）

 思路：已求总和超过目标和，就不需要继续了。

for(int i=startIndex;i<=9 && sum

6.分割回文串

 解法1：前后指针+回溯

class Solution {
private:
        //判断是不是回文串,利用双指针
        bool isPartition(const string& s,int start,int end){
           for(int i=start,j=end;i=s.size()){
            ans.push_back(path);
            return;
        }
        
        for(int i=startIndex;i path;
    vector> ans;
public:
    vector> partition(string s) {
       //path.clear();
       //ans.clear();
       backTracking(s,0);
       return ans;
    }
};

• 时间复杂度：O(n×2^n)，其中 n 是字符串 s 的长度。在最坏情况下，s 包含 n 个完全相同的字符，因此它的任意一种划分方法都满足要求。而长度为 n 的字符串的划分方案数为 2^(n−1)=O(2^n)，每一种划分方法需要 O(n) 的时间求出对应的划分结果并放入答案，因此总时间复杂度为 O(n×2^n)。
• 空间复杂度：O(n^2)，数组 ans 需要使用的空间为 O(n^2)，而在回溯的过程中，我们需要使用 O(n) 的栈空间以及 O(n) 的用来存储当前字符串分割方法的空间。由于 O(n) 在渐进意义下小于 O(n^2)，因此空间复杂度为 O(n^2))。

7.复原IP地址

 解法1：回溯

class Solution {
private:
     //判断子串是否合法  ,  左闭右闭[start,end]
     bool isValid(const string& s,int start,int end){
         if(start>end){return false;}
         //1、0开头的数字,不合法
         if(s[start]=='0' && start!=end){return false;}     //s[start]==0 是错误代码
         int num=0;
         for(int i=start;i<=end;i++){
             //2、遇到非数字字符,不合法
             //if(s[i]<'0' || s[i]>'9'){return false;}     
             //3、如果大于255,不合法
             num=num*10+(s[i]-'0');    //(s[i]-'0') 字符转化为数字
             if(num>255){return false;}
         }
         return true;
     }
     // startIndex: 搜索的起始位置，pointNum:添加小数点的数量
    void backTracking(string& s,int startIndex,int pointNum){//此处不能定义为 const string& s
        if(pointNum==3){   // 小数点数量为3时，分隔结束
            // 判断第四段子字符串是否合法，如果合法就放进result中
            if(isValid(s,startIndex,s.size()-1)){   //因为是左闭右闭的区间，所以用 s.size()-1
                ans.push_back(s);
            }
            return;
        }
        for(int i=startIndex;i ans;
public:
    vector restoreIpAddresses(string s) {
       //ans.clear();
       //if(s.size()>12) return ans;
       backTracking(s,0,0);
       return ans;
    }
};

8.*子集

 

解法1：回溯

class Solution {
private:
    void backTracking(vector& nums,int startIndex){
        ans.push_back(path);            // 收集子集，要放在终止添加的上面，否则会漏掉自己
        // if(startIndex>=nums.size()){return;}   终止条件可以不加，因为本层for循环本来也结束了
        for(int i=startIndex;i path;
    vector> ans;
public:
    vector> subsets(vector& nums) {
     //path.clear();
     //ans.clear();
     backTracking(nums,0);
     return ans;
    }
};

• 时间复杂度：O(n×2^n)，一共 2^n 个状态，每种状态需要 O(n) 的时间来构造子集。
• 空间复杂度：O(n)，临时数组 path 需要使用的空间为 O(n)，递归时栈空间的代价为 O(n)。

9.子集II

 

 解法1：回溯（startIndex去重）

class Solution {
private:
    void backTracking(vector& nums,int startIndex){
        ans.push_back(path);
        unordered_set set;  //利用set去重
        for(int i=startIndex;istartIndex && nums[i]==nums[i-1]){continue;} 
            path.push_back(nums[i]);
            backTracking(nums,i+1);
            path.pop_back();
        }

    }
    vector path;
    vector> ans;
public:
    vector> subsetsWithDup(vector& nums) {
      //path.clear();
      //ans.clear();
      sort(nums.begin(),nums.end()); //去重需要提前排序
      backTracking(nums,0);
      return ans;
    }
};

• 时间复杂度：O(n×2^n)，其中 n 是数组 nums 的长度。排序的时间复杂度为 O(nlog⁡n)。最坏情况下 nums 中无重复元素，需要枚举其所有 2^n 个子集，每个子集加入答案时需要拷贝一份，耗时 O(n)，一共需要 O(n×2^n)+O(n)=O(n×2^n) 的时间来构造子集。由于在渐进意义上 O(nlog⁡n) 小于 O(n×2^n)，故总的时间复杂度为 O(n×2^n)。
• 空间复杂度：O(n)，临时数组 path 需要使用的空间为 O(n)，递归时栈空间的代价为 O(n)。

解法2：回溯（used去重） 

class Solution {
private:
    void backTracking(vector& nums,int startIndex,vector& used){
        ans.push_back(path);
        for(int i=startIndex;i0 && nums[i]==nums[i-1] && used[i-1]==false){continue;} 
            path.push_back(nums[i]);
            used[i]=true;   //true 代表同一树枝使用过
            backTracking(nums,i+1,used);
            used[i]=false;
            path.pop_back();
        }
    }
    vector path;
    vector> ans;
public:
    vector> subsetsWithDup(vector& nums) {
      //path.clear();
      //ans.clear();
      vector used(nums.size(),false);
      sort(nums.begin(),nums.end()); //去重需要提前排序
      backTracking(nums,0,used);
      return ans;
    }
};

解法3：回溯（set去重）

class Solution {
private:
    void backTracking(vector& nums,int startIndex){
        ans.push_back(path);
        unordered_set set;  //利用set去重
        for(int i=startIndex;i path;
    vector> ans;
public:
    vector> subsetsWithDup(vector& nums) {
      //path.clear();
      //ans.clear();
      sort(nums.begin(),nums.end()); //去重需要提前排序
      backTracking(nums,0);
      return ans;
    }
};

10.*全排列

排列问题的特点：

• 每层都是从0开始搜索而不是startIndex
• 需要used数组记录path里都放了哪些元素

解法1：回溯

class Solution {
private:
    void backTracking(vector& nums,vector& used){
        if(path.size()==nums.size()){
            ans.push_back(path);
            return;
        }
        for(int i=0;i path;
    vector> ans;
public:
    vector> permute(vector& nums) {
     //path.clear();
     //ans.clear();
     vector used(nums.size(),false);
     backTracking(nums,used);
     return ans;
    }
};

• 时间复杂度：O(n×n!)，其中 n 是序列的长度。backTracking 的调用次数是 O(n!) 。而对于 backTracking 调用的每个叶结点（共 n! 个），我们需要将当前答案使用 O(n) 的时间复制到答案数组中，相乘得时间复杂度为 O(n×n!)。
• 空间复杂度：O(n)，递归时栈空间的代价为 O(n)。

11.全排列II

 解法1：回溯

思路：如果要对树层中前一位去重，就用used[i - 1] == false，如果要对树枝前一位去重用used[i - 1] == true。

对于排列问题，树层上去重和树枝上去重，都是可以的，但是树层上去重效率更高！

class Solution {
private:
    void backTracking(vector& nums,vector& used){
        if(path.size()==nums.size()){
            ans.push_back(path);
            return;
        }
        for(int i=0;i0 && nums[i]==nums[i-1] && used[i-1]==false){continue;}
            if(used[i]==false){  //注意：保证没有被使用过
                path.push_back(nums[i]);
                used[i]=true;
                backTracking(nums,used);
                used[i]=false;
                path.pop_back();          
            }*/
            if((i>0 && nums[i]==nums[i-1] && used[i-1]==false) || used[i]==true){continue;}
                path.push_back(nums[i]);
                used[i]=true;
                backTracking(nums,used);
                used[i]=false;
                path.pop_back();      
        }
    }
    vector path;
    vector> ans;
public:
    vector> permuteUnique(vector& nums) {
     //path.clear();
     //ans.clear();
     sort(nums.begin(),nums.end());
     vector used(nums.size(),false);
     backTracking(nums,used);
     return ans;
    }
};

• 时间复杂度：O(n×n!)，其中 n 是序列的长度。backTracking 的调用次数是 O(n!) 。而对于 backTracking 调用的每个叶结点（共 n! 个），我们需要将当前答案使用 O(n) 的时间复制到答案数组中，相乘得时间复杂度为 O(n×n!)。
• 空间复杂度：O(n)，递归时栈空间的代价为 O(n)。

12.#字符串的排列

 解法1：回溯

class Solution {
private:
    void backTracking(string& s,vector& used){
        if(path.size()==s.size()){
            ans.push_back(path); return;
        }
        for(int i=0;i0&&s[i-1]==s[i]&&used[i-1]==false) || used[i]==true){continue;}
            path.push_back(s[i]);
            used[i]=true;
            backTracking(s,used);
            used[i]=false;
            path.pop_back();
        }
    }
    vector ans;
    string path;
public:
    vector permutation(string s) {
        sort(s.begin(),s.end()); //字符串可以直接排序
        vector used(s.size(),false);
        backTracking(s,used);
        return ans;
    }
};

13.N皇后

 

 解法1：回溯

class Solution {   
private:
    //判断是不是N皇后
    //1、不能同行
    //2、不能同列
    //3、不能同斜线 （45度和135度角）
    bool isValid(vector& chessboard,int row,int col,int n){
        //检查列（不必检查行）
        for(int i=0;i=0 && j>=0; i--,j--){
            if(chessboard[i][j]=='Q'){return false;}
        }
        //检查 135度角是否有皇后(副斜线)
        for(int i=row-1,j=col+1;i>=0 && j& chessboard,int n,int row){
      if(row==n){
          ans.push_back(chessboard);   //存放结果
          return;
      }
      //棋盘的宽度就是for循环的长度，递归的深度就是棋盘的高度
      for(int col=0;col> ans;
public:
    vector> solveNQueens(int n) {
      //ans.clear();
      vector chessboard(n,string(n,'.'));  //重点
      backTracking(chessboard,n,0);
      return ans;
    }
};

• 时间复杂度：O(n!)，其中 n 是皇后数量。
• 空间复杂度：O(n)，递归时栈空间的代价为 O(n)。

14.N皇后 II

 解法1：回溯

class Solution {
private:
    //判断是否为N皇后
    bool isValid(vector& chessboard,int row,int col,int n){
        for(int i=0;i=0 && j>=0;--i,--j){
            if(chessboard[i][j]=='Q') return false;
        }
        for(int i=row-1,j=col+1;i>=0 && j& chessboard,int n,int row){
        if(row==n){
           count++;    //ans.push_back(chessboard); 存放结果
           return; 
        }
        for(int col=0;col chessboard(n,string(n,'.'));
        backTraversal(chessboard,n,0);
        return count;
    }
};

• 时间复杂度：O(n!)，其中 n 是皇后数量。
• 空间复杂度：O(n)，递归时栈空间的代价为 O(n)。

15.解数独

 

 解法1：回溯

class Solution {
private:
    //判断棋盘是否合法
    bool isValid(vector>& board,int row,int col,char val){
        //1、判断行中是否重复
        for(int i=0;i<9;++i){
            if(board[row][i]==val){return false;}
        }
        //2、判断列中是否重复
        for(int j=0;j<9;++j){
            if(board[j][col]==val){return false;}
        }
        //3、判断9宫格中是否重复
        int startRow=(row/3)*3;
        int startCol=(col/3)*3;
        for(int i=startRow;i>& board){
        for(int i=0;i>& board) {
      backTracking(board);
    }
};

 

解法2：回溯（带输入输出）

#include
using namespace std;
//判断棋盘是否合法
bool isValid(vector>& board,int row,int col,char val){
//1、判断行中是否重复
for(int i=0;i<9;++i){
    if(board[row][i]==val){return false;}
}
//2、判断列中是否重复
for(int j=0;j<9;++j){
    if(board[j][col]==val){return false;}
}
//3、判断9宫格中是否重复
int startRow=(row/3)*3;
int startCol=(col/3)*3;
for(int i=startRow;i>& board){
     for(int i=0;i> board(9,vector(9));
    for(int i=0;i<9;++i){
        for(int j=0;j<9;++j){
            cin>>board[i][j];
        }
    }
    
    backTracking(board);
    
    for(int i=0;i<9;++i){
        for(int j=0;j<9;++j){
            cout<

16.递增子序列

 解法1：回溯

思路：本题求自增子序列，是不能对原数组经行排序的，排完序的数组都是自增子序列了，所以不能使用之前的去重逻辑！

class Solution {
private:
    void backTracking(vector& nums,int startIndex){
        if(path.size()>1){
            ans.push_back(path);
        }  //注意这里不要加return ，要取树上的节点
        unordered_set uset;  //去重
        for(int i=startIndex;i path;
    vector> ans;
public:
    vector> findSubsequences(vector& nums) {
      //path.clear();
      //ans.clear();
      backTracking(nums,0);
      return ans;
    }
}

• 时间复杂度：O(n×2^n)，需要 O(n) 的时间添加到答案中。
• 空间复杂度：O(n)，临时数组的空间代价是 O(n)，递归使用的栈空间的空间代价也是 O(n)。

17.重新安排行程

 解法1：回溯

class Solution {
private:
    // bool类型：因为我们只需要找到一个行程，就是在树形结构中唯一的一条通向叶子节点的路线
    bool backTracking(int ticketNum,vector& ans){ //ticketNum，表示有多少个航班
        if(ans.size()==ticketNum+1){return true;}    //机场个数=航班数量+1 ，说明找到了一个行程    
        for(pair& target : targets[ans[ans.size()-1]]){ //pair里要有const，因为map中的key是不可修改的
            if(target.second>0){   //飞机还可以飞（航班次数的增减，判断是否飞过）
                ans.push_back(target.first);
                target.second--;
                if(backTracking(ticketNum,ans)) return true;
                target.second++;
                ans.pop_back();   
            }
        }
        return false;
    }
    // unordered_map<出发机场, map<到达机场, 航班次数>> targets
    unordered_map> targets;
public:
    vector findItinerary(vector>& tickets) {
      //targets.clear();
      vector ans;     
      for(const vector& vec:tickets){targets[vec[0]][vec[1]] ++ ;}  //记录映射关系
      ans.push_back("JFK");  //起始机场

      backTracking(tickets.size(),ans);
      return ans;
    }
};

18.*括号生成 

 解法1：回溯

思路：列举所有可能结果，想到用回溯。剪枝：左括号小于右括号，提前退出

class Solution {
private:    
    void backTraversal(string& s,int left,int right,int n){
        //左括号数⽬等于右括号数⽬ => 左括号数⽬ + 右括号数⽬ = 2 * n
        if(s.size()==2*n) {
            ans.push_back(s);
            return;
        }
        if(left){
            s.push_back('(');
            backTraversal(s,left-1,right,n);
            s.pop_back();
        }
        if(left ans;
public:
    vector generateParenthesis(int n) {
        string s;
        backTraversal(s,n,n,n);
        return ans;
    }
};

• 时间复杂度：O(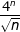)，需要 O(n) 的时间添加到答案中。
• 空间复杂度：O(n)，除了答案数组之外，我们所需要的空间取决于递归栈的深度，每一层递归函数需要 O(1) 的空间，最多递归 2n 层，因此空间复杂度为 O(n)。

19.*单词搜索

解法1：回溯

 思路：设函数 check(i,j,k) 表示判断以网格的 (i,j) 位置出发，能否搜索到单词 word[k..]，其中 word[k..] 表示字符串 word 从第 k 个字符开始的后缀子串。如果能搜索到，则返回 true，反之返回 false。

class Solution {
private:
    bool check(vector>& board,vector>& visited,string &s,int i,int j,int k){
        if(board[i][j]!=s[k]){
            return false;
        }else if(k==s.length()-1){
            return true;
        }
        //为了防止重复遍历相同的位置，需要 visited 数组，用于标识每个位置是否被访问过。
        visited[i][j]=true;   //表示已经访问
        bool ans=false;    
        vector> directions{{0,1},{0,-1},{-1,0},{1,0}};   //重要：表示 上下左右 遍历网格
        for(const auto& dir: directions){
            int new_i=i+dir.first, new_j=j+dir.second;   //重要：表示 上下左右 遍历网格
            int row=board.size(),col=board[0].size();
            if(new_i>=0 && new_i=0 &&new_j>& board, string word) {
        int row=board.size(),col=board[0].size();
        vector> visited(row,vector(col));
        for(int i=0;i

• 时间复杂度：一个非常宽松的上界为 O(mn⋅3L)，其中 m,n 为网格的长度与宽度，L 为字符串 word 的长度。在每次调用函数 check 时，除了第一次可以进入 4 个分支以外，其余时间我们最多会进入 3 个分支（因为每个位置只能使用一次，所以走过来的分支没法走回去）。由于单词长为 L，故 check(i,j,0) 的时间复杂度为 O(3L)，而我们要执行 O(mn) 次检查。然而，由于剪枝的存在，我们在遇到不匹配或已访问的字符时会提前退出，终止递归流程。因此，实际的时间复杂度会远远小于 O(mn⋅3L)。
• 空间复杂度：O(mn)，额外开辟 O(mn) 的 visited 数组，同时栈的深度最大为 O(min⁡(L,mn))。

20.#矩阵中的路径

 

 解法1：回溯

class Solution {
private:
    bool check(vector>& board,vector>& visited,string &s,int i,int j,int k){
        if(board[i][j]!=s[k]){
            return false;
        }else if(k==s.length()-1){
            return true;
        }
        //为了防止重复遍历相同的位置，需要 visited 数组，用于标识每个位置是否被访问过。
        visited[i][j]=true;   //表示已经访问
        bool ans=false;    
        vector> directions{{0,1},{0,-1},{-1,0},{1,0}};   //重要：表示 上下左右 遍历网格
        for(const auto& dir: directions){
            int new_i=i+dir.first, new_j=j+dir.second;   //重要：表示 上下左右 遍历网格
            int row=board.size(),col=board[0].size();
            if(new_i>=0 && new_i=0 &&new_j>& board, string word) {
        int row=board.size(),col=board[0].size();
        vector> visited(row,vector(col));
        for(int i=0;i

题型十五：贪心

1.分发饼干

 

解法1：排序+贪心

避免使用两个for循环的技巧： 用了一个index来控制饼干数组的遍历，遍历饼干并没有再起一个for循环，而是采用自减的方式。

class Solution {      //大饼干留给胃口大的
public:
    int findContentChildren(vector& g, vector& s) {
       sort(g.begin(),g.end());
       sort(s.begin(),s.end());
       
       int ans=0;
       int index=s.size()-1;    //饼干数组的下标
       for(int i=g.size()-1; i>=0; i--){
          if(index>=0 && s[index]>=g[i]){
              ans++;
              index--;
          }
       }
       return ans;
    }
};

class Solution {      //小饼干留给胃口小的
public:
    int findContentChildren(vector& g, vector& s) {
       sort(g.begin(),g.end());
       sort(s.begin(),s.end());

       int ans=0;
       for(int i=0; i=g[ans]){
              ans++;
          }
       }
       return ans;
    }
};

• 时间复杂度：O(mlog⁡m+nlog⁡n)，其中 m 和 n 分别是数组 g 和 s 的长度。对两个数组排序的时间复杂度是 O(mlog⁡m+nlog⁡n)，遍历数组的时间复杂度是 O(m+n)，因此总时间复杂度是 O(mlog⁡m+nlog⁡n)。
• 空间复杂度：O(log⁡m+log⁡n)，空间复杂度主要是排序的额外空间开销。

2.K次取反后最大化的数组和

解法1：贪心

class Solution {
static bool cmp(int a,int b){  //一定要加 static
    return abs(a)>abs(b);
}
public:
    int largestSumAfterKNegations(vector& nums, int k) {
       sort(nums.begin(),nums.end(),cmp);   //将数组按绝对值由大到小的顺序排列
       //将数组中的负数取反
       for(int i=0;i0){
               nums[i] *=-1;
               k--;
           }
       }
       //k还大于0，且为奇数，反转数组最后一个最小的数
       if(k%2==1)  nums[nums.size()-1] *=-1;

       int ans=0;
       for(int num:nums) ans+=num;
       return ans;
    }
};

3.柠檬水找零

解法1：贪心

class Solution {
public:
    bool lemonadeChange(vector& bills) {
        int five=0,ten=0;
        for(int bill: bills){
            if(bill==5){five++;}
            if(bill==10){
                if(five>0){
                    ten++;
                    five--;
                }else return false;
            }
            // 优先消耗10美元，因为5美元的找零用处更大，能多留着就多留着(此处用到贪心)
            if(bill==20){
                if(five>0 && ten>0){
                    five--;
                    ten--;
                }
                else if(five>=3){five-=3;}
                else return false;
            }
        }
        return true;
    }
};

• 时间复杂度：O(n)，其中 n 是 bills 的长度。
• 空间复杂度：O(1)

4.摆动序列

解法1：贪心

思路：我们记录当前序列的上升下降趋势。每次加入一个新元素时，用新的上升下降趋势与之前对比，如果出现了「峰」或「谷」，答案加一，并更新当前序列的上升下降趋势。

class Solution {
public:
    int wiggleMaxLength(vector& nums) {
       if(nums.size()<=1)  return nums.size();
       int curDiff=0;   //记录当前一对的差值
       int preDiff=0;   //记录前一对的差值（初始化为0）
       int ans=1;       //记录峰值个数，序列默认，最右侧有一个峰值

       for(int i=0;i0 && preDiff<=0) || (curDiff<0 && preDiff>=0)){
              ans++;
              preDiff=curDiff;
          }
       }
       return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是序列的长度。我们只需要遍历该序列一次。
• 空间复杂度：O(1)，只需要常数空间来存放若干变量。

解法2：动态规划

up[i] ：第i个元素结尾的最长的「上升摆动序列」的长度。（最后一个元素为 峰）

down[i]：第i个元素结尾的最长的「下降摆动序列」的长度。（最后一个元素为 谷）

class Solution {   
public:
    int wiggleMaxLength(vector& nums) {
        int n=nums.size();
        if(n<=1)  return n;
        vector up(n,1),down(n,1);
        for(int i=1;inums[i-1]){
                up[i]=max(up[i-1],down[i-1]+1);
                down[i]=down[i-1];
            }else if(nums[i]

• 时间复杂度：O(n)，其中 n 是序列的长度。我们只需要遍历该序列一次。
• 空间复杂度：O(n)，需要开辟两个长度为 n 的数组。

解法3：动态规划（优化）

思路：前一种动态规划中，我们仅需要前一个状态来进行转移，所以我们维护两个变量即可。注意到每有一个「峰」到「谷」的下降趋势，down 值才会增加，且过程中 down与 up 的差的绝对值差恒不大于 1，即 up≤down+1，于是有 max⁡(up,down+1)=down+1。这样我们可以省去不必要的比较大小的过程。

class Solution {   
public:
    int wiggleMaxLength(vector& nums) {
        int n=nums.size();
        if(n<=1)  return n;
        int up=1,down=1;
        for(int i=1;inums[i-1]){
                up=down+1;
            }else if(nums[i]

• 时间复杂度：O(n)，其中 n 是序列的长度。我们只需要遍历该序列一次。
• 空间复杂度：O(1)，只需要常数空间来存放若干变量。

5.单调递增的数字

 

 解法1：贪心

class Solution {
public:
    int monotoneIncreasingDigits(int n) {
       string strNum=to_string(n);    //转化为字符串操作更方便
       // flag用来标记赋值9从哪里开始
       int flag=strNum.size();
       for(int i=strNum.size()-1;i>0;i--){
           if(strNum[i-1]>strNum[i]){
               flag=i;
               strNum[i-1]--;  // 赋值9的前一位，需要相应的减1
           }
       }

       for(int i=flag;i

• 时间复杂度：O(n)，其中 n 是数字长度。
• 空间复杂度：O(n)，需要一个字符串。

6.分发糖果

 

解法1：贪心

思路：评分更高的孩子必须比他两侧的邻位孩子获得更多的糖果 => 正反遍历

        1、从左到右遍历，只比较右边孩子评分比左边大的情况。

        2、从右到左遍历，只比较左边孩子评分比右边大的情况。

class Solution {
public:
    int candy(vector& ratings) {
        vector candyVec(ratings.size(),1); //至少有1个糖果
        for(int i=1;iratings[i-1]) candyVec[i]=candyVec[i-1]+1;
        }       
        for(int j=ratings.size()-1;j>0;--j){
            if(ratings[j-1]>ratings[j]) candyVec[j-1]=max(candyVec[j-1],candyVec[j]+1);
        }

        int ans=0;
        for(int i=0;i

• 时间复杂度：O(n)，其中 n 是孩子的数量。我们需要遍历两次数组以分别计算满足正反遍历的最少糖果数量。
• 空间复杂度：O(n)，需要保存所有的正向遍历对应的糖果数量。

7.根据身高重建队列

 解法1：贪心

思路：遇到两个维度权衡的时候，一定要先确定一个维度，再确定另一个维度。按照身高排序之后，优先按身高高的people的k来插入。后序插入节点也不会影响前面已经插入的节点，最终按照k的规则完成了队列。

排序完的people： [[7,0], [7,1], [6,1], [5,0], [5,2]，[4,4]]

插入的过程：

• 插入[7,0]：[[7,0]]
• 插入[7,1]：[[7,0],[7,1]]
• 插入[6,1]：[[7,0],[6,1],[7,1]]
• 插入[5,0]：[[5,0],[7,0],[6,1],[7,1]]
• 插入[5,2]：[[5,0],[7,0],[5,2],[6,1],[7,1]]
• 插入[4,4]：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]

class Solution {
public:
    static bool cmp(const vector a,const vector b){
        if(a[0]==b[0])  return a[1]b[0];                  //身高降序排列
    }
    vector> reconstructQueue(vector>& people) {
        sort(people.begin(),people.end(),cmp);
        vector> ans;
        for(int i=0;i

• 时间复杂度：O(n^2)，其中 n 是数组 people的长度。我们需要 O(nlog⁡n)的时间进行排序，随后需要 O(n^2) 的时间遍历每一个人并将他们放入队列中。由于前者在渐近意义下小于后者，因此总时间复杂度为 O(n^2)。
• 空间复杂度：O(logn)。

8.*跳跃游戏

 解法1：贪心

思路：局部最优解：每次取最大跳跃步数（取最大覆盖范围），

          整体最优解：最后得到整体最大覆盖范围，看是否能到终点 

class Solution {
public:     
    bool canJump(vector& nums) {
       if(nums.size()==1) return true;   //只有一个元素，必定可以达到
       int cover=0;
       for(int i=0;i<=cover;++i){
           cover=max(i+nums[i],cover);   //i+nums[i] 表示该位置的覆盖范围
           if(cover>=nums.size()-1) return true;
       }
       return false;
    }
};

• 时间复杂度：O(n)，其中 n 是数组的大小。只需要访问 nums 数组一遍，共 n 个位置。
• 空间复杂度：O(1)，不需要额外的空间开销。

9.跳跃游戏II

 

 解法1：贪心

思路：在具体的实现中，我们维护当前能够到达的最大下标位置，记为边界。我们从左到右遍历数组，到达边界时，更新边界并将跳跃次数增加 1。在遍历数组时，我们不访问最后一个元素，这是因为在访问最后一个元素之前，我们的边界一定大于等于最后一个位置，否则就无法跳到最后一个位置了。

class Solution {
public:
    int jump(vector& nums) {
       int cur=0,next=0,ans=0;
       //控制移动下标i只移动到 nums.size()-2 的位置，所以移动下标只要遇到当前覆盖最远距离的下标，直接步数加一。
       for(int i=0;i

• 时间复杂度：O(n)，其中 n 是数组的大小。只需要访问 nums 数组一遍，共 n 个位置。
• 空间复杂度：O(1)，不需要额外的空间开销。

10.用最少数量的箭引爆气球

 解法1：排序+贪心

class Solution {
private:
    static bool cmp(const vector& a,const vector& b){return a[0]>& points) {
       if(points.size()==0) return 0;
       sort(points.begin(),points.end(),cmp);   //按照Xstart进行由小到大的排序
       int ans=1;
       for(int i=1;i

• 时间复杂度：O(nlog⁡n)，其中 n 是数组 points 的长度。排序的时间复杂度为 O(nlog⁡n)，对所有气球进行遍历并计算答案的时间复杂度为 O(n)，其在渐进意义下小于前者，因此可以忽略。
• 空间复杂度：O(log⁡n)，即为排序需要使用的栈空间。

11.无重叠区间

 

解法1： 排序+贪心

 思路：（逆向思维）右边界排序，从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。因为右边界越小越好，只要右边界越小，留给下一个区间的空间就越大，所以从左向右遍历，优先选右边界小的。   （左右边界排序都可以）

class Solution {  
private:   
    static bool cmp(const vector& a,const vector& b) {return a[1]>& intervals) {
       if(intervals.size()==0) return 0;
       sort(intervals.begin(),intervals.end(),cmp);
       int count=1;      // points不为空，至少需要一支箭
       for(int i=1;i

• 时间复杂度：O(nlog⁡n)，其中 n 是区间的数量。我们需要 O(nlog⁡n) 的时间对所有的区间按照右端点进行升序排序，并且需要 O(n) 的时间进行遍历。由于前者在渐进意义下大于后者，因此总时间复杂度为 O(nlog⁡n)。
• 空间复杂度：O(log⁡n)，即为排序需要使用的栈空间。

12.划分字母区间

 

 解法1：贪心

思路：统计每一个字符最后出现的位置；从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点

class Solution {
public:
    vector partitionLabels(string s) {
      int hash[26]={0};
      for(int i=0;i ans;
      int left=0,right=0;
      for(int i=0;i

• 时间复杂度：O(n)，其中 n 是字符串的长度。需要遍历字符串两次，第一次遍历时记录每个字母最后一次出现的下标位置，第二次遍历时进行字符串的划分。
• 空间复杂度：O(∣Σ∣)，其中 Σ 是字符串中的字符集。这道题中，字符串只包含小写字母，因此 ∣Σ∣=26。

13.*合并区间

 

解法1：排序+贪心

class Solution {
private:
    static bool cmp(const vector& a,const vector& b){return a[0]> merge(vector>& intervals) {
       if(intervals.size()==0) return {};
       sort(intervals.begin(),intervals.end(),cmp);
       // 排序的参数使用了lamda表达式
       //sort(intervals.begin(), intervals.end(), [](const vector& a, const vector& b){return a[0] < b[0];});
       vector> ans;
       ans.push_back(intervals[0]);
       for(int i=1;i

• 时间复杂度：O(nlog⁡n)，其中 n 是区间的数量。除去排序的开销，我们只需要一次线性扫描，所以主要的时间开销是排序的 O(nlog⁡n)。
• 空间复杂度：O(log⁡n)，即为排序需要使用的栈空间。

14.最大子数组和(最大子序列和)

解法1：贪心

class Solution {
public:
    int maxSubArray(vector& nums) {
      int ans=INT_MIN;
      int count=0;
      for(int i=0;ians) ans=count;  // 取区间累计的最大值（相当于不断确定最大子序终止位置）
          if(count<=0) count=0;     // 相当于重置最大子序起始位置，因为遇到负数一定是拉低总和
      }
      return ans;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

解法2：动态规划

dp[i]： 以第 i 个数结尾的「连续子数组的最大和」

class Solution {
public:
    int maxSubArray(vector& nums) {    
        vector dp(nums.size());  //此处 +1 可有可无
        dp[0]=nums[0];
        int ans=dp[0];  //此处不是定义为 INT_MIN
        for(int i=1;ians) ans=dp[i];
        }
        return ans;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(n)，需要一个数组来保存 dp[i] 的值。

解法3：动态规划（优化）

思路：考虑到 dp[i] 只和 dp[i−1] 相关，于是我们可以只用一个变量 pre 来维护对于当前 dp[i] 的 dp[i−1] 的值是多少，从而让空间复杂度降低到 O(1)。

class Solution {
public:
    int maxSubArray(vector& nums) {
        int pre=0,maxAns=nums[0];    //考虑了唯一值为负值
        for(const auto &num:nums){   //用num读取容器vector的值
           pre=max(pre+num,num);
           maxAns=max(pre,maxAns);
        }
        return maxAns;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

15.#连续子数组的最大和

16.加油站

解法1：暴力

class Solution {
public:
    int canCompleteCircuit(vector& gas, vector& cost) {
        //for循环适合模拟从头到尾的遍历，而while循环适合模拟环形遍历
        for(int i=0;i0 && i!=index){
                rest+=gas[index]-cost[index];
                index=(index+1)%cost.size();
            }
            if(rest>=0 && i==index) return i;
        }
        return -1;
    }
};

• 时间复杂度：O(n^2)
• 空间复杂度：O(1)

解法2：贪心

 思路：局部最优：当前累加rest[i]的和curSum一旦小于0，起始位置至少要是i+1，因为从i开始一定不行。全局最优：直到找到可以跑一圈的起始位置。

class Solution {
public:
    int canCompleteCircuit(vector& gas, vector& cost) {
        int start=0,curSum=0,totalSum=0;
        for(int i=0;i

• 时间复杂度：O(n)
• 空间复杂度：O(1)

17.监控二叉树

 

解法1：贪心

 思路：局部最优：让叶子节点的父节点安摄像头，所用摄像头最少，整体最优：全部摄像头数量所用最少！使用后序遍历也就是左右中的顺序，可以在回溯的过程中实现从下到上进行推导。

假设：0表示该节点无监控，1表示本节点有监控 （ 注意空节点上是判定为有监控 ），2表示本节点有摄像头。则将有以下8种情况：

一： 左右节点都有监控， 则中间节点应该是0（无监控的状态）

（1） left == 1 && right == 1

二： 左右节点至少有一个有摄像头，则其父节点就应该是1（监控的状态）

（2） left == 1 && right == 2

（3） left == 2 && right == 1

三：左右节点至少有一个无监控的情况，则中间节点（父节点）应该是2（放摄像头）

（4） left == 0 && right == 0     左右节点无监控

（5） left == 0 && right == 1 

（6） left == 0 && right == 2

（7） left == 1 && right == 0

（8） left == 2 && right == 0

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * }; */
class Solution {    //if 的顺序很重要 
private:
    int Traversal(TreeNode* node){
       if(node==nullptr) return 1;
       int left=Traversal(node->left),right=Traversal(node->right);
       if(left==0 || right==0){          //1、需要添加摄像头的情况：至少有一个节点没有监控
           ans++;
           return 2;
       }
       if(left==1 && right==1) return 0; //2、左右节点都有监视    
       if(left==2 || right==2) return 1; //3、左右节点至少有一个有摄像头
       return -1;    //逻辑不会走到这里，但需要有这一步
    }
    int ans=0;
public:   
    int minCameraCover(TreeNode* root) {
       if(Traversal(root)==0) {ans++;}   //4、根节点没有被监视
       return ans;
    }
};

class Solution {
private:
    int Traversal(TreeNode* node){
       if(node==nullptr) return 1;
       int left=Traversal(node->left),right=Traversal(node->right);
       //使用else就不能把各个分支的情况展示出来，出错几率小
       if(left==0 || right==0){   
            ans++;
            return 2;
       }else if(left==1 && right==1){
            return 0;
       }else{
            return 1;
       }
    }
    int ans=0;
public:   
    int minCameraCover(TreeNode* root) {
       if(Traversal(root)==0) {ans++;}   //根节点没有被监视
       return ans;
    }
};

18.Dota2 参议院

解法1：贪心

class Solution {
public:
    string predictPartyVictory(string senate) {
        bool R=true,D=true;   // R = true表示本轮循环结束后，字符串里依然有R ; D同理
        //用一个变量flag记录当前参议员之前有几个敌人，进而判断自己是否被消灭了
        //flag>0 : R可以消灭D ， 反之亦然
        int flag=0;
        while(R && D){     // 一旦R或者D为false，就结束循环，说明本轮结束后只剩下R或者D了
            R=false,D=false;
            for(int i=0;i0) senate[i]=0;
                    else D=true;
                    flag--;
                }
            }
        }
        return R==true?"Radiant":"Dire";   // 循环结束之后，R和D只能有一个为true
    }
};

• 时间复杂度：O(n)，其中 n 是字符串 senate 的长度。
• 空间复杂度：O(1)

19.分割平衡字符串

 解法1：贪心

class Solution {
public:
    int balancedStringSplit(string s) {
        int ans=0,count=0;
        for(int i=0;i

20.@删除被覆盖区间

思路：在 lj=li 时，第 i 个区间还是有可能被出现在其之后的区间覆盖的。一种常用的解决方法是将区间按照左端点为第一关键字且递增、右端点为第二关键字且递减进行排序。此时对于第 i 个区间 [li,ri)，出现在其之后的区间 [lj,rj) 即使满足 lj=li，但根据新的排序规则，一定有 rj区间 [li,ri) 不可能被任何出现在其之后的区间覆盖。

解法1：排序+贪心

class Solution {
public:
    int removeCoveredIntervals(vector>& intervals) {
        int n = intervals.size();
        sort(intervals.begin(), intervals.end(), [](const vector& u, const vector& v) {
            return u[0] < v[0] || (u[0] == v[0] && u[1] > v[1]);
        });
        int ans = n;
        int rmax = intervals[0][1];
        for (int i = 1; i < n; ++i) {
            if (intervals[i][1] <= rmax) {
                --ans;
            }
            else {
                rmax = max(rmax, intervals[i][1]);
            }
        }
        return ans;
    }
};

• 时间复杂度：O(nlogn)，其中 n 是区间的个数。
• 空间复杂度：O(logn)，为排序需要的空间。

题型十六：动态规划

 0.动态规划的基础知识

 （1）动态规划，英文：Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。所以动态规划中每一个状态一定是由上一个状态推导出来的。

（2）动态规划5步曲

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

（3）动态规划主要解决的题型：打家劫舍、背包、股票、子序列

1.斐波那契数

解法1：递归

class Solution {
public:
    int fib(int n) {
       if(n<2) return n;
       return fib(n-1)+fib(n-2);
    }
};

• 时间复杂度：O(2^n)
• 空间复杂度：O(n)

解法2：动态规划

优化思路：由于 F(n) 只和 F(n−1) 与 F(n−2) 有关，因此可以使用「滚动数组思想」把空间复杂度优化成 O(1)。

class Solution {
public:
    int fib(int n) {
      if(n<2) return n;
      vector dp(n+1);
      dp[0]=0,dp[1]=1;
      for(int i=2;i<=n;++i){
          // dp[i]=dp[i-1]+dp[i-2];
          int sum=dp[0]+dp[1];
          dp[0]=dp[1];
          dp[1]=sum;
      }
      return dp[1];
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

 2.#斐波那契数列

 解法1：动态规划

class Solution {
public:
    int fib(int n) {
        int MOD=1000000007;
        if(n<2) return n;
        vector dp(n+1);
        dp[0]=0;dp[1]=1;
        for(int i=2;i<=n;++i){
            int sum=(dp[0]+dp[1])%MOD; //不同之处
            dp[0]=dp[1];
            dp[1]=sum;
        }
        return dp[1];
    }
};

3.爬楼梯

 

解法1：动态规划

思路：用 f(x) 表示爬到第 x 级台阶的方案数，考虑最后一步可能跨了一级台阶，也可能跨了两级台阶，所以我们可以列出如下式子：f(x)=f(x−1)+f(x−2)。它意味着爬到第 x 级台阶的方案数是爬到第 x−1 级台阶的方案数和爬到第 x−2 级台阶的方案数的和。因为每次只能爬 1 级或 2 级，所以 f(x) 只能从 f(x−1) 和 f(x−2) 转移过来。

class Solution {
public:
    int climbStairs(int n) {
      vector dp(n+1);
      dp[0]=1;dp[1]=1;
      for(int i=2;i<=n;++i){
          //利用滚动数组，降低空间复杂度
          int sum=dp[0]+dp[1];
          dp[0]=dp[1];
          dp[1]=sum;
      }
      return dp[1];
    }
};

 解法2：动态规划（完全背包）

class Solution {
public:
    int climbStairs(int n) {
       vector dp(n+1,0);
       dp[0]=1;    //完全背包记得初始化(完全背包是物品可以重复使用)
       for(int i=1;i<=n;++i){      //先遍历背包
           //进阶：2表示每次最多可以爬2个台阶
           for(int j=1;j<=2;++j){  //再遍历物品
               if(i-j>=0)  dp[i]+=dp[i-j];
           }
       }
       return dp[n];
    }
};

4.#青蛙跳台阶问题

 解法1：动态规划

class Solution {
public:
    int numWays(int n) {
        int MOD=1000000007;
        int p=0,q=1,r=1;
        for(int i=2;i<=n;++i){
            p=q;
            q=r;
            r=(p+q)%MOD;
        }
        return r;
    }
};

class Solution {
public:
    int numWays(int n) {
        int MOD=1000000007;
        if(n==0) return 1;
        vector dp(n+1);
        dp[0]=1;dp[1]=1;
        for(int i=2;i<=n;++i){
            int sum=(dp[0]+dp[1])%MOD; //不同之处
            dp[0]=dp[1];
            dp[1]=sum;
        }
        return dp[1];
    }
};

5. #把数字翻译成字符串

 解法1：动态规划

思路：字符串的第 i 位置的翻译规则：

(1)可以单独作为一位来翻译：单独翻译对 f(i) 的贡献为 f(i−1)；
(2)如果第 i−1 位和第 i 位组成的数字在 10 到 25 之间，可以把这两位连起来翻译：如果第 i−1 位存在，并且第 i−1 位和第 i 位形成的数字 x 满足 10≤x≤25，那么就可以把第 i−1 位和第 i 位连起来一起翻译，对 f(i) 的贡献为 f(i−2)，否则为 0。f(i)=f(i−1)+f(i−2)

class Solution {
public:
    int translateNum(int num) {
        int a=1,b=1,c;
        int x,y=num%10;
        while(num!=0){
            num/=10;
            x=num%10;

            c=(10<=(10*x+y) && (10*x+y)<=25) ? a+b :a;
            //滑动数组优化空间
            b=a;
            a=c;

            y=x;
        }
        return a;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

6.使用最小花费爬楼梯

 解法1：动态规划

class Solution {
public:
    int minCostClimbingStairs(vector& cost) {
       int n=cost.size();
       vector dp(n+1);
       //由于可以选择下标 0 或 1 作为初始阶梯，因此有 dp[0]=dp[1]=0
       // 默认第一步都是不花费体力的，最后一步花费体力
       dp[0]=0;   
       dp[1]=0;       
       for(int i=2;i<=n;++i){
           dp[i]=min(dp[i-2]+cost[i-2],dp[i-1]+cost[i-1]) ;
       }
       return dp[n];  
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(n)

解法2：动态规划（优化）

class Solution {
public:
    int minCostClimbingStairs(vector& cost) {
       int n=cost.size();
       int pre=0,cur=0;
       for(int i=2;i<=n;++i){
           int next=min(pre+cost[i-2],cur+cost[i-1]) ;
           pre=cur;
           cur=next;
       }
       return cur;  
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

7.*不同路径

 解法1：动态规划

class Solution {
public:
    int uniquePaths(int m, int n) {
       vector>  dp(m,vector(n));  //定义二维数组
       for(int i=0;i

• 时间复杂度：O(mn)
• 空间复杂度：O(mn)

8.不同路径II

 

 解法1：动态规划

class Solution {
public:
    int uniquePathsWithObstacles(vector>& obstacleGrid) {
        //取一个二维数组的横坐标数和纵坐标数
        int m=obstacleGrid.size();
        int n=obstacleGrid[0].size();
        vector> dp(m,vector(n,0));  //初始化为0
        //一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作
        for(int i=0;i

• 时间复杂度：O(mn)
• 空间复杂度：O(mn)

9.*最小路径和

 解法1：动态规划

思路： dp[i][j] 表示从左上角出发到 (i,j) 位置的最小路径和

class Solution {    
public:
    int minPathSum(vector>& grid) {
        //注意二维数组 行和列的定义
        int row=grid.size(),col=grid[0].size();       
        if(row==0 && col==0) return 0;
        vector> dp(row+1,vector(col+1));
        dp[0][0]=grid[0][0];       
        for(int j=1;j

• 时间复杂度：O(mn)
• 空间复杂度：O(mn)

10.#礼物的最大价值

 解法1：动态规划

class Solution {
public:
    int maxValue(vector>& grid) {
        int row=grid.size(),col=grid[0].size();
        vector> dp(row+1,vector(col+1));
        dp[0][0]=grid[0][0];
        for(int j=1;j

11.整数拆分

 解法1：动态规划

思路：对于的正整数 n，当 n≥2 时，可以拆分成至少两个正整数的和。令 k 是拆分出的第一个正整数，则剩下的部分是 n−k 可以不继续拆分，或者继续拆分成至少两个正整数的和。

特别地，0 不是正整数，1 是最小的正整数，0 和 1 都不能拆分，因此 dp[0]=dp[1]=0。

class Solution {
public:
    int integerBreak(int n) {
       vector dp(n+1);
       dp[2]=1;     //初始化 dp[0]=dp[1]=1   没有意义
       for(int i=3;i<=n;++i){
           for(int j=1;j

• 时间复杂度：O(n^2)
• 空间复杂度：O(n)

12.#剪绳子

 解法1：动态规划

class Solution {
public:
    int cuttingRope(int n) {
        vector dp(n+1); //必须 +1
        dp[2]=1;
        for(int i=3;i<=n;++i){
            for(int j=1;j

• 时间复杂度：O(n^2)
• 空间复杂度：O(n)

解法2：贪心（数学规律）

 思路：（1）将绳子 以相等的长度等分为多段 ，得到的乘积最大。（2）尽可能将绳子以长度 3 等分为多段时，乘积最大。

a) 当 n≤3 时，按照规则应不切分，但由于题目要求必须剪成 m>1 段，因此必须剪出一段长度为 1 的绳子，即返回 n−1 。
b) 当 n>3 时，求 n 除以 3 的 整数部分 a 和 余数部分 b （即 n=3a+b ），并分为以下三种情况：

    1) 当 b=0 时，直接返回 3^a；
    2) 当 b=1 时，要将一个 1+3 转换为 2+2，因此返回 3^{a-1} ×4；
    3) 当 b=2 时，返回 3^a ×2。

class Solution {
public:
    int cuttingRope(int n) {
        if(n<=3) return n-1;
        int a=n/3,b=n%3;  //n=3a+b
        if(b==0){
            return (int)pow(3,a);
        }else if(b==1){
            return (int)pow(3,a-1)*4;
        }else{
            return (int)pow(3,a)*2;
        }
    }
};

• 时间复杂度：O(1)。涉及到的操作包括计算商和余数，以及幂次运算，时间复杂度都是常数。
• 空间复杂度：O(1)。只需要使用常数复杂度的额外空间。

13.#剪绳子II

 解法1：贪心

思路：不适合用动态规划，大数越界的求余问题

class Solution {
public:
    int cuttingRope(int n) {
        if(n<=3) return n-1;
        int MOD=1000000007;
        int a=n/3,b=n%3;  
        long ans=1; //防止溢出 一定是long
        for(int i=1;i

14.*不同的二叉搜索树

解法1：动态规划

思路：给定一个有序序列 1⋯n，为了构建出一棵二叉搜索树，我们可以遍历每个数字 i，将该数字作为树根，将 1⋯(i−1) 序列作为左子树，将 (i+1)⋯n 序列作为右子树。接着我们可以按照同样的方式递归构建左子树和右子树。在上述构建的过程中，由于根的值不同，因此我们能保证每棵二叉搜索树是唯一的。

class Solution {
public:
    int numTrees(int n) {
      vector dp(n+1);
      dp[0]=1;   //空树
      for(int i=1;i<=n;++i){
          for(int j=1;j<=i;++j){
              //j-1 为以 j 为头结点左子树节点数量， i-j 为以 j 为头结点右子树节点数量
              dp[i] += dp[j-1]*dp[i-j]; 
          }
      }
      return dp[n];
    }
};

• 时间复杂度：O(n^2)
• 空间复杂度：O(n)

15.分割等和子集

 解法1：动态规划(0-1背包)

class Solution {
public:
    bool canPartition(vector& nums) {
        int n=nums.size(),sum=0;
        if(n<2) return false;
        for(auto &num:nums){sum+=num;}
        if(sum%2==1) return false;
        int target=sum/2;

        // dp[i]中的i表示背包内总和,初始化为0
        vector dp(target+1,0);
        //开始0-1背包 
        //使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒叙遍历！
        for(int i=0;i=nums[i];--j){
                dp[j]=max(dp[j],dp[j-nums[i]]+nums[i]);
            }
        }
        //传统的「0−1 背包问题」要求选取的物品的重量之和  不能超过  背包的总容量，
        //这道题则要求选取的数字的和  恰好等于  整个数组的元素和的一半
        if(dp[target]==target) return true;
        return false;
    }
};

• 时间复杂度：O(n×target)，其中 n 是数组的长度，target 是整个数组的元素和的一半。需要计算出所有的状态，每个状态在进行转移时的时间复杂度为 O(1)。
• 空间复杂度：O(target)，其中 target 是整个数组的元素和的一半。空间复杂度取决于 dp 数组，在不进行空间优化的情况下，空间复杂度是 O(n×target)，在进行空间优化的情况下，空间复杂度可以降到 O(target)。

16.最后一块石头的重量

解法1：动态规划(0-1背包)

class Solution {
public:
    int lastStoneWeightII(vector& stones) {
       int sum=0;
       for(auto &stone:stones){sum+=stone;}
       int target=sum/2;
       vector dp(target+1,0);  //初始化为0
       for(int i=0;i=stones[i];--j){   //再遍历背包，必须还是倒序遍历
               dp[j]=max(dp[j],dp[j-stones[i]]+stones[i]);
           }
       }
       //分成两堆石头，一堆石头的总重量是dp[target]，另一堆就是sum - dp[target]。
       //在计算target的时候，target = sum / 2 因为是向下取整，所以sum - dp[target] 一定是大于等于dp[target]的。
       return (sum-dp[target])-dp[target];
    }
};

• 时间复杂度：O(n×target)，其中 n 是数组的长度，target 是整个数组的元素和的一半。需要计算出所有的状态，每个状态在进行转移时的时间复杂度为 O(1)。
• 空间复杂度：O(target)，其中 target 是整个数组的元素和的一半。

17.*目标和

解法1:回溯

思路:数组 nums 的每个元素都可以添加符号 + 或 -，因此每个元素有 2 种添加符号的方法，n 个数共有 2^n 种添加符号的方法，对应 2^n 种不同的表达式。当 n 个元素都添加符号之后，即得到一种表达式，如果表达式的结果等于目标数 target，则该表达式即为符合要求的表达式。

class Solution {
private:
    void backTracking(vector& candidates,int target,int startIndex,int sum){
        if(sum==target){ans.push_back(path);}
        for(int i=startIndex;i> ans;
    vector path;
public:
    int findTargetSumWays(vector& nums, int target) {
       int sum=0;
       for(auto &num:nums) sum+=num;
       //没有此方案
       if(target>sum || (target+sum)%2) return 0;
       //left + right等于sum，而sum是固定的。
       //left - (sum - left) = target    =>    left = (target + sum)/2 
       //目标和问题 转化为 组合求和问题
       int bagSize=(target+sum)/2;

       sort(nums.begin(),nums.end());
       backTracking(nums,bagSize,0,0);
       return ans.size();
    }
};

• 时间复杂度：O(2^n)，其中 n 是数组 nums 的长度。回溯需要遍历所有不同的表达式，共有 2^n 种不同的表达式，每种表达式计算结果需要 O(1) 的时间，因此总时间复杂度是 O(2^n)。
• 空间复杂度：O(n)，其中 n 是数组 nums 的长度。空间复杂度主要取决于递归调用的栈空间，栈的深度不超过 n。

解法2:动态规划(0-1背包)

要点:在求装满背包有几种方法的情况下，递推公式一般为：dp[ j ] += dp[ j-nums[i] ]

class Solution {
public:
    int findTargetSumWays(vector& nums, int target) {
       int sum=0;
       for(auto &num:nums) sum+=num;
       if(abs(target)>sum || (target+sum)%2) return 0;
       //问题转化为 装满容量为bagSize 背包，有几种方法
       int bagSize=(target+sum)/2;
       vector dp(bagSize+1,0);  //初始化为0 , dp[j] 才能正确的由dp[j - nums[i]]推导出来
       dp[0]=1;     //装满容量为0的背包，有1种方法，就是装0件物品

       for(int i=0;i=nums[i];--j){
               dp[j]+=dp[j-nums[i]];
           }
       }
       return dp[bagSize];  //装满容器为bagSize背包，有  dp[bagSize]  种方法
    }
};

• 时间复杂度：O(n×bagSize)，其中 n 是数组 nums的长度。
• 空间复杂度：O(bagSize)。

18.一和零

 

 解法1:动态规划(0-1背包)

class Solution {
public:
    int findMaxForm(vector& strs, int m, int n) {
         vector> dp(m+1,vector(n+1,0));   //默认初始化为0
         for(string str:strs){   //1、遍历物品
             int zeroNum=0,oneNum=0;  
             for(char c:str){
                if(c=='0') zeroNum++;
                else oneNum++;
             }
            //2、 遍历背包容量且从后向前遍历。
            //与典型的0-1背包问题不同的是，这个物品的重量有两个维度,一个是m 一个是n，而不同长度的字符串就是不同大小的待装物品
            for(int i=m;i>=zeroNum;--i){
                for(int j=n;j>=oneNum;--j){
                  //dp[i][j] 可以由前一个strs里的字符串推导出来，strs里的字符串有zeroNum个0，oneNum个1。
                  //dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。
                  dp[i][j]=max(dp[i][j],dp[i-zeroNum][j-oneNum]+1);
                }
            }
        }
        return dp[m][n];
    }
};

• 时间复杂度：O(lmn+L)，其中 l 是数组 strs 的长度，m 和 n 分别是 0 和 1 的容量，L 是数组 strs 中的所有字符串的长度之和。动态规划需要计算的状态总数是 O(lmn)，每个状态的值需要 O(1) 的时间计算。对于数组 strs 中的每个字符串，都要遍历字符串得到其中的 0 和 1 的数量，因此需要 O(L) 的时间遍历所有的字符串。总时间复杂度是 O(lmn+L)。
• 空间复杂度：O(mn)，其中 m 和 n 分别是 0 和 1 的容量。使用空间优化的实现，需要创建 m+1 行 n+1 列的二维数组 dp。

19.*零钱兑换

解法1: 动态规划(完全背包)

思路:dp[j] ：凑足总额为j所需钱币的最少个数为dp[j] ; dp[j]必须初始化为一个最大的数，否则就会在min(dp[j] , dp[j - coins[i]] + 1 )比较的过程中被初始值覆盖 ; 凑足总额为j - coins[i]的最少个数为dp[j - coins[i]]，只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j]

class Solution {
public:
    int coinChange(vector& coins, int amount) {
        vector dp(amount+1,INT_MAX);    
        dp[0]=0;   //凑足总金额为0  所需钱币的个数一定是0
        for(int i=0;i

• 时间复杂度：O(n×m)，其中 n 是面值数,m为题目所给的总金额。我们一共需要计算 O(m) 个状态，m 对于每个状态，每次需要枚举 n 个面额来转移状态，所以一共需要O(mn) 的时间复杂度。
• 空间复杂度：O(m),数组 dp 需要开长度为总金额 m 的空间.

20.零钱兑换II

解法1:动态规划(完全背包)

//求组合数  就是外层for循环遍历物品，内层for遍历背包。

//求排列数  就是外层for遍历背包，内层for循环遍历物品。

//此题需要求组合数，与顺序无关

求装满背包有几种方法，一般公式都是：dp[j] += dp[j - nums[i]]

class Solution {
public:
    int change(int amount, vector& coins) {
        //下标非0的dp[j]初始化为0，这样累计加dp[j - coins[i]]的时候才不会影响真正的dp[j]
        vector dp(amount+1,0);  
        dp[0]=1;   //凑成总金额0的货币组合数为1
        for(int i=0;i

• 时间复杂度：O(n×m)，其中 n 是面值数,m为题目所给的总金额。我们一共需要计算 O(m) 个状态，m 对于每个状态，每次需要枚举 n 个面额来转移状态，所以一共需要O(mn) 的时间复杂度。
• 空间复杂度：O(m),数组 dp 需要开长度为总金额 m 的空间.

21.组合总和IV

 解法1:动态规划(完全背包)

class Solution {
public:
    int combinationSum4(vector& nums, int target) {
        vector dp(target+1,0);
        dp[0]=1;

        //完全背包，数可以无限的用，此处求和是错误的
        //int sum=0;
        //for(auto &num:nums){sum+=num;}
        //if(sum=0 && dp[i]

• 时间复杂度：O(n×m)，其中 n 是面值数,m为题目所给的总金额。
• 空间复杂度：O(m),数组 dp 需要开长度为总金额 m 的空间.

22.*完全平方数

 解法1:动态规划(完全背包1)

 思路:本题同零钱兑换一样,组合和排列一样,不需要考虑是先遍历物品还是先遍历背包

class Solution {
public:
    int numSquares(int n) {
       //dp[i]：和为i的完全平方数的最少数量为dp[i]
       vector dp(n+1,INT_MAX);
       dp[0]=0;
       //先遍历物品，再遍历背包
       for(int i=1;i*i<=n;++i){
           for(int j=1;j<=n;++j){
               if(j-i*i>=0)
               dp[j]=min(dp[j],dp[j-i*i]+1);
           }
       }
       return dp[n];
    }
};

• 时间复杂度：O(n​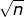)，其中 n 为给定的正整数。状态转移方程的时间复杂度为 O(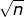)，共需要计算 n 个状态，因此总时间复杂度为 O(n​)。
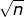• 空间复杂度：O(n),我们需要 O(n) 的空间保存状态。

解法2:动态规划(完全背包2)

class Solution {
public:
    int numSquares(int n) {
       //dp[i]：和为i的完全平方数的最少数量为dp[i]
       vector dp(n+1,INT_MAX);
       dp[0]=0;
       //先遍历背包，再遍历物品
       for(int i=1;i<=n;++i){
           for(int j=1;j*j<=i;++j){
              dp[i]=min(dp[i],dp[i-j*j]+1);
           }
       }
       return dp[n];
    }
};

23.*单词拆分

 解法1:动态规划(完全背包)

思路:对于检查一个字符串是否出现在给定的字符串列表里一般可以考虑哈希表来快速判断.

class Solution {
public:
    bool wordBreak(string s, vector& wordDict) {
         unordered_set wordDictSet(wordDict.begin(),wordDict.end());
         int n=s.size();
         vector dp(n+1,false);
         dp[0]=true;
         //先遍历背包，再遍历物品。因为要求子串
         for(int i=1;i<=n;++i){
             for(int j=0;j

• 时间复杂度：O(n^2) ，其中 n 为字符串 s 的长度。我们一共有 O(n) 个状态需要计算，每次计算需要枚举 O(n) 个分割点，哈希表判断一个字符串是否出现在给定的字符串列表需要 O(1) 的时间，因此总时间复杂度为 O(n^2)。
• 空间复杂度：O(n)，其中 n 为字符串 s 的长度。我们需要 O(n)的空间存放 dp 值以及哈希表亦需要 O(n) 的空间复杂度，因此总空间复杂度为 O(n)。

24.*打家劫舍

解法1:动态规划

思路: (1) 如果只有一间房屋，则偷窃该房屋，可以偷窃到最高总金额。如果只有两间房屋，则由于两间房屋相邻，不能同时偷窃，只能偷窃其中的一间房屋，因此选择其中金额较高的房屋进行偷窃，可以偷窃到最高总金额。

(2) 如果房屋数量大于两间，有两个选项：

    a) 偷窃第 k 间房屋，那么就不能偷窃第 k−1 间房屋，偷窃总金额为前 k−2 间房屋的最高总金额与第 k 间房屋的金额之和。b) 不偷窃第 k 间房屋，偷窃总金额为前 k−1 间房屋的最高总金额。

在两个选项中选择偷窃总金额较大的选项，该选项对应的偷窃总金额即为前 k 间房屋能偷窃到的最高总金额。

class Solution {
public:
    int rob(vector& nums) {
       int n=nums.size();
       if(n==0) return 0;
       if(n==1) return nums[0];
       vector dp(n);
       dp[0]=nums[0];
       dp[1]=max(nums[0],nums[1]);
       for(int i=2;i

• 时间复杂度：O(n) ，其中 n 是数组长度。只需要对数组遍历一次。
• 空间复杂度：O(n)

25.打家劫舍II

 解法1:动态规划

class Solution {
public:
    int rob(vector& nums) {
        int n=nums.size();
        if(n==0) return 0;
        if(n==1) return nums[0];
        int ans1=robRange(nums,0,n-2);  //情况1：包含首元素，不包含尾元素
        int ans2=robRange(nums,1,n-1);  //情况2：不包含首元素，包含尾元素
        //以上两种情况包含情况3：既不含首元素，又不含尾元素
        return max(ans1,ans2);
    }

    int robRange(vector& nums,int start,int end){
        if(start==end) return nums[start];
        vector dp(nums.size());
        dp[start]=nums[start];
        dp[start+1]=max(nums[start],nums[start+1]);
        for(int i=start+2;i

• 时间复杂度：O(n) ，其中 n 是数组长度。只需要对数组遍历两次。
• 空间复杂度：O(n)

26.*打家劫舍III

 解法1:动态规划+后序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * }; */
class Solution {
public:
    int rob(TreeNode* root) {
        //dp数组就是一个长度为2的数组,
        //下标为0记录 不偷该节点 所得到的的最大金钱，
        //下标为1记录  偷该节点  所得到的的最大金钱
        vector ans=robTree(root);
        return max(ans[0],ans[1]);
    }
    vector robTree(TreeNode* node){
        if(node==nullptr) return vector{0, 0};
        //后序遍历树
        vector left=robTree(node->left);
        vector right=robTree(node->right);

        //偷该节点 => 左右子树不能偷
        int val1=node->val + left[0] + right[0];
        //不偷该节点 => 左右孩子就可以偷，至于到底偷不偷一定是选一个最大的
        int val2=max(left[1],left[0]) + max(right[1],right[0]);
        return {val2,val1};
    }
};

• 时间复杂度：O(n) ，其中 n 是二叉树的节点个数。对二叉树做了一次后序遍历，时间复杂度是 O(n)。
• 空间复杂度：O(n) ，递归会使用到栈空间，空间代价是 O(n)。

27.*买卖股票的最佳时机

 解法1:贪心

class Solution {   //贪心：最左最小值，最右最大值
public:
    int maxProfit(vector& prices) {
       int ans=0;
       int low=INT_MAX;
       for(int i=0;i

• 时间复杂度：O(n) ，只需要遍历一次。
• 空间复杂度：O(1) ，只使用了常数个变量。

解法2:动态规划

思路:注意这里说的是“持有”，“持有”不代表就是当天“买入”！也有可能是昨天就买入了，今天保持持有的状态.  二维数组: 0表示 不持有, 1表示 持有

class Solution {
public:
     //dp[i][0] : 第i天 不持有 股票所得最多现金
     //dp[i][1] : 第i天 持有 股票所得最多现金
    int maxProfit(vector& prices) {
       int len=prices.size();
       if(len==0) return 0;
       vector>  dp(len,vector(2));
       //第0天不持有股票，不持有股票那么现金就是0   
       dp[0][0]=0;
       //第0天持有股票，此时的持有股票就一定是买入股票了
       dp[0][1]=-prices[0];

       for(int i=1;i

• 时间复杂度：O(n) 。
• 空间复杂度：O(n) ，dp[i] 只是依赖于 dp[i - 1] 的状态 , 有能力再优化。

28.买卖股票的最佳时机II

解法1:贪心

class Solution {     //局部最优：收集每天的正利润，全局最优：求得最大利润
public:
    int maxProfit(vector& prices) {
       int ans=0;
       for(int i=1;i

• 时间复杂度：O(n) ，只需要遍历一次。
• 空间复杂度：O(1) ，只使用了常数个变量。

解法2:动态规划

class Solution {
public:
     //dp[i][0] : 第i天 不持有 股票所得最多现金
     //dp[i][1] : 第i天 持有 股票所得最多现金
    int maxProfit(vector& prices) {
       int len=prices.size();
       if(len==0) return 0;
       vector> dp(len,vector(2));
       dp[0][0]=0;
       dp[0][1]=-prices[0];   //注意此处为负值
       for(int i=1;i

• 时间复杂度：O(n) 。
• 空间复杂度：O(n) ，dp[i] 只是依赖于 dp[i - 1] 的状态 , 有能力再优化。

29.买卖股票的最佳时机III

 解法1:动态规划

思路:  一天一共就5种状态 :

0、没有操作  1、第一次买入  2、第一次卖出  3、第二次买入  4、第二次卖出

dp[i][j]中 i 表示第i天，j为 [0 - 4] 五个状态，dp[i][j]表示第i天状态j所剩最大现金

无论题目中是否允许「在同一天买入并且卖出」这一操作，最终的答案都不会受到影响，这是因为这一操作带来的收益为零。

class Solution {
public:
    int maxProfit(vector& prices) {
        int n=prices.size();
        if(n==0) return 0;
        vector> dp(n,vector(5,0));  //初始值为0
        dp[0][1]=-prices[0];
        dp[0][3]=-prices[0];   //注意
        for(int i=1;i

• 时间复杂度：O(n) ，其中 n 是数组 prices 的长度。
• 空间复杂度：O(n) 。

30.买卖股票的最佳时机IV

 解法1:动态规划

class Solution {
public:
    int maxProfit(int k, vector& prices) {
       int len=prices.size();
       if(len==0) return 0;
       vector> dp(len,vector(2*k+1,0));
       for(int j=1;j<2*k;j+=2){
           dp[0][j]-=prices[0];
       }
       for(int i=1;i

• 时间复杂度：O(nmin⁡(n,k))，其中 n 是数组 prices 的大小，即我们使用二重循环进行动态规划需要的时间。
• 空间复杂度：O(nmin⁡(n,k)) 。

31.*最佳买卖股票时机含冷冻期

解法1:动态规划

class Solution {
public:
     //0、买入
     //1、卖出：两天前就卖出了股票，度过了冷冻期，一直没操作，今天保持卖出股票状态
     //2、卖出：今日卖出
     //3、冷冻期
    int maxProfit(vector& prices) {
       int len=prices.size();
       if(len==0) return 0;
       vector> dp(len,vector(4,0));
       dp[0][0]-=prices[0];
       for(int i=1;i

• 时间复杂度：O(n)。
• 空间复杂度：O(n) 。

解法2:动态规划(官方)

class Solution {
public:
     //0、持有股票后的最多现金
     //1、不持有股票（能购买）的最多现金
     //2、不持有股票（冷冻期）的最多现金
    int maxProfit(vector& prices) {
       int len=prices.size();
       if(len==0) return 0;
       vector> dp(len,vector(3,0));
       dp[0][0]-=prices[0];
       for(int i=1;i

• 时间复杂度：O(n)，其中 n 为数组 prices 的长度。
• 空间复杂度：O(n) ，我们需要 3n 的空间存储动态规划中的所有状态，对应的空间复杂度为 O(n)。如果使用空间优化，空间复杂度可以优化至 O(1)。

32.买卖股票的最佳时机含手续费

解法1:贪心

class Solution {
public:
    int maxProfit(vector& prices, int fee) {
        int ans=0;
        int minPrice=prices[0]+fee;
        for(int i=1;iminPrice){
               ans+=prices[i]-minPrice;
               //看成当前手上拥有一支买入价格为 prices[i]的股票，将 minPrice 更新为 prices[i]。
               //这样一来，如果下一天股票价格继续上升，我们会获得 prices[i+1]−prices[i]的收益，
               //加上这一天 prices[i]−minPrice的收益，恰好就等于在这一天不进行任何操作，而在下一天卖出股票的收益；
               minPrice=prices[i];
           }
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 为数组 prices 的长度。
• 空间复杂度：O(1) 。

解法2:动态规划

class Solution {
public:
     //dp[i][0] : 第i天 不持有 股票所得最多现金
     //dp[i][1] : 第i天 持有 股票所得最多现金
    int maxProfit(vector& prices, int fee) {
        int len=prices.size();
        if(len==0) return 0;
        vector> dp(len,vector(2,0));
        dp[0][1]-=prices[0];
        for(int i=1;i

• 时间复杂度：O(n)，其中 n 为数组 prices 的长度。
• 空间复杂度：O(n) 。

33.股票的最大利润

解法1:贪心

class Solution {
public:
    int maxProfit(vector& prices) {
        int len=prices.size();
        if(len==0) return 0;
        int low=INT_MAX,ans=0;
        for(int i=0;i

解法2:动态规划

class Solution {
public:
    int maxProfit(vector& prices) {
        int len=prices.size();
        if(len==0) return 0;
        vector> dp(len+1,vector(2,0));
        dp[0][1]=-prices[0];
        for(int i=1;i

34.最长递增子序列

 解法1:动态规划

class Solution {    //dp[i] ：i之前 包含i 的最长严格递增子序列的长度
public:
    int lengthOfLIS(vector& nums) {
        int len=nums.size();
        if(len==0) return 0;
        vector dp(len,1);
        int ans=1;
        for(int i=0;i

• 时间复杂度：O(n^2)，其中 n 为数组 nums 的长度。动态规划的状态数为 n，计算状态 dp[i] 时，需要 O(n) 的时间遍历 dp[0…i−1] 的所有状态，所以总时间复杂度为 O(n^2)。
• 空间复杂度：O(n) ，需要额外使用长度为 n 的 dp 数组。

35.最长连续递增序列

解法1:贪心

class Solution {
public:
    int findLengthOfLCIS(vector& nums) {
        int len=nums.size();
        if(len==0) return 0;
        int ans=1,count=1;
        for(int i=0;inums[i]){
                count++;
            }else{count=1;}
            ans=max(ans,count);
            //if(count>ans) ans=count;
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是数组 nums 的长度。需要遍历数组一次。
• 空间复杂度：O(1) ，额外使用的空间为常数。

 解法2:动态规划

class Solution {
public: 
    int findLengthOfLCIS(vector& nums) {
        int len=nums.size();
        if(len==0) return 0;
        vector dp(len,1);
        int ans=1;
        for(int i=0;inums[i]){ //求“连续”递增的特别之处：相邻元素相比
                dp[i+1]=dp[i]+1;
            }
            ans=max(ans,dp[i+1]);
        }
        return ans;
    }
};

• 时间复杂度：O(n)，其中 n 是数组 nums 的长度。需要遍历数组一次。
• 空间复杂度：O(n) 。

36.最长递增子序列的个数

 

 解法1:动态规划

class Solution {
public:
    int findNumberOfLIS(vector& nums) {
        int len=nums.size(),maxLen=0,ans=0;
        if(len<=1) return len;
        //dp[i] 用于记录最长递增子序列的长度； count[i] 用于记录最长递增子序列的个数
        vector dp(len,1),count(len,1);
        for(int i=0;inums[j]){
                    //同时考虑 dp[i] 与 count[i] 的更新
                    if(dp[j]+1>dp[i]){    //找到一个更长的递增子序列
                        dp[i]=dp[j]+1;
                        count[i]=count[j];     //重置计数:以j为结尾的子串的最长递增子序列的个数，就是最新的以i为结尾的子串的最长递增子序列的个数
                    }else if(dp[j]+1==dp[i]){  //找到两个相同长度的递增子序列
                        count[i]+=count[j]; //以i为结尾的子串的最长递增子序列的个数 就应该加上以j为结尾的子串的最长递增子序列的个数
                    }
                }
            }
            //统计结果
            if(dp[i]>maxLen){
                maxLen=dp[i];
                ans=count[i]; //重置计数
            }else if(dp[i]==maxLen){
                ans+=count[i];
            }
        }
        return ans;   
    }
};

• 时间复杂度：O(n^2)，其中 n 为数组 nums 的长度。
• 空间复杂度：O(n) ，需要额外使用长度为 n 的 dp 数组。

37.最长重复子数组

 解法1:动态规划

思路: 题目事实上就是求连续子序列, 动态规划最拿手

class Solution {
public:
    int findLength(vector& nums1, vector& nums2) {
        int len1=nums1.size(),len2=nums2.size();
        vector> dp(len1+1,vector(len2+1,0));
        int ans=0;
        for(int i=1;i<=len1;++i){     //从1开始，需要考虑相等的情况
            for(int j=1;j<=len2;++j){
                if(nums1[i-1]==nums2[j-1]){  //与求最大公共子序列不同：不需要考虑不相等的情况
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                ans=max(ans,dp[i][j]);
            }
        }
        return ans;
    }
};

• 时间复杂度：O(mn)，其中 m 为数组 nums1 的长度，n 为数组 nums2 的长度。
• 空间复杂度：O(mn) 。

38.最长公共子序列

 解法1:动态规划

思路:  最长公共子序列问题是典型的二维动态规划问题。dp[i][j]：长度为[0, i-1]的字符串text1与长度为[0, j-1]的字符串text2的最长公共子序列为dp[i][j]( 不是[0,i] 是为了方便后面 )

class Solution {  
public:
    int longestCommonSubsequence(string text1, string text2) {
        int len1=text1.length(),len2=text2.length();
        vector> dp(len1+1,vector(len2+1,0));  // 定义2维数组必须 +1
        for(int i=1;i<=len1;++i){
            for(int j=1;j<=len2;++j){
                //两种情况：text1[i-1] 和 text2[j-1] 相同或者不同
                if(text1[i-1]==text2[j-1]){
                    dp[i][j] = dp[i-1][j-1] + 1 ;
                }else {
                    dp[i][j] = max( dp[i][j-1] , dp[i-1][j] ) ;  //特别注意不相等的情况
                }
            }
        }
        return dp[len1][len2];
    }
};

• 时间复杂度：O(mn)，其中 m 为字符串 text1 的长度，n 为字符串 text2 的长度。二维数组 dp 有 m+1 行和 n+1 列，需要对 dp 中的每个元素进行计算。
• 空间复杂度：O(mn) ，创建了 m+1 行 n+1 列的二维数组 dp。

39.不相交的线

 解法1:动态规划

思路: 直线不能相交，这就是说明在字符串A中 找到一个与字符串B相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，链接相同数字的直线就不会相交。本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度。

class Solution {
public:
    int maxUncrossedLines(vector& nums1, vector& nums2) {
        int len1=nums1.size(),len2=nums2.size();
        vector> dp(len1+1,vector(len2+1,0));  // 定义2维数组必须 +1
        for(int i=1;i<=len1;++i){
            for(int j=1;j<=len2;++j){
                if(nums1[i-1]==nums2[j-1]){
                    dp[i][j] = dp[i-1][j-1] + 1 ;
                }else {
                    dp[i][j] = max( dp[i][j-1] , dp[i-1][j] ) ;
                }
            }
        }
        return dp[len1][len2];
    }
};

• 时间复杂度：O(mn)，其中 m 为字符串 text1 的长度，n 为字符串 text2 的长度。二维数组 dp 有 m+1 行和 n+1 列，需要对 dp 中的每个元素进行计算。
• 空间复杂度：O(mn) ，创建了 m+1 行 n+1 列的二维数组 dp。

40.判断子序列

 解法1:动态规划

思路:  编辑距离中,只涉及删除,不涉及增加  替换

class Solution {
public:
    //dp[i][j] : 以下标 i-1 为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]
    //因为这样的定义在dp二维矩阵中可以留出初始化的区间
    bool isSubsequence(string s, string t) {
        int len1=s.length(),len2=t.length();
        vector> dp(len1+1,vector(len2+1,0));
        for(int i=1;i<=len1;++i){
            for(int j=1;j<=len2;++j){
                if(s[i-1]==t[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }else{
                    dp[i][j]=dp[i][j-1];    //此处相当于把t[j-1]删除,dp[i][j] 的数值就是 看s[i-1]与 t[j-2]的比较结果
                }
            }
        }
        return dp[len1][len2]==len1 ? true : false ;
    }
};

• 时间复杂度：O(mn)，其中 m 为 s 的长度，n 为 t 的长度。
• 空间复杂度：O(mn)

 解法2:双指针

思路: 初始化两个指针 i 和 j，分别指向 s 和 t 的初始位置。每次贪心地匹配，匹配成功则 i 和 j 同时右移，匹配 s 的下一个位置，匹配失败则 j 右移，i 不变，尝试用 t 的下一个字符匹配 s。最终如果 i 移动到 s 的末尾，就说明 s 是 t 的子序列。

class Solution {
public:
    bool isSubsequence(string s, string t) {
        int len1=s.length(),len2=t.length();
        int i=0,j=0;
        while(i

• 时间复杂度：O(m+n)，其中 m 为 s 的长度，n 为 t 的长度。每次无论是匹配成功还是失败，都有至少一个指针发生右移，两指针能够位移的总距离为 m+n。
• 空间复杂度：O(1) 。

41.不同的子序列

 解法1:动态规划

思路:  题目如果不是子序列，而是要求连续序列，那就可以考虑用KMP 。只有删除,没有增加替换

class Solution {
public:
    //dp[i][j]：以i-1为结尾的s子序列中 出现以j-1为结尾的t的个数
    int numDistinct(string s, string t) {
        int len1=s.size(),len2=t.length();
        if(len1> dp(len1+1,vector(len2+1));   //必须记得  +1
        //题干中有:题目数据保证答案符合 32 位带符号整数范围。   故不可以用 int / long
        //vector> dp(len1+1,vector(len2+1));
        //dp[i][0] 表示：以i-1为结尾的s可以删除所有元素，出现空字符串的个数为1
        //dp[0][j]：空字符串s可以随便删除元素，出现以j-1为结尾的字符串t的个数为0
        //特别的： dp[0][0]=1
        for(int i=0;i<=len1;++i) dp[i][0]=1;
        //for(int j=1;j

class Solution {
public:
    int numDistinct(string s, string t) {
        int len1=s.size(),len2=t.length();
        if(len1> dp(len1+1,vector(len2+1));   
        for(int i=0;i<=len1;++i) dp[i][0]=1;
        for(int i=1;i<=len1;++i){
            for(int j=1;j<=len2;++j){
                if(s[i-1]==t[j-1]){
                    dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
                }else{
                    dp[i][j]=dp[i-1][j];
                }
            }
        }
        return dp[len1][len2];
    }
};

• 时间复杂度：O(mn)，其中 m 和 n 分别是字符串 s 和 t 的长度。二维数组 dp 有 m+1 行和 n+1 列，需要对 dp 中的每个元素进行计算。
• 空间复杂度：O(mn)，其中 m 和 n 分别是字符串 s 和 t 的长度。创建了 m+1 行 n+1 列的二维数组 dp。

42.两个字符串的删除操作

 

 解法1:动态规划

 思路: dp[i][j]：以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，想要达到相等，所需要删除元素的  最少次数

class Solution {
public:
    int minDistance(string word1, string word2) {
        int len1=word1.length(),len2=word2.length();
        vector> dp(len1+1,vector(len2+1));
        for(int i=0;i<=len1;++i) dp[i][0]=i;
        for(int j=0;j<=len2;++j) dp[0][j]=j;
        for(int i=1;i<=len1;++i){
            for(int j=1;j<=len2;++j){
                //去掉一个字符公共字符之后，最少删除操作次数不变，因此 dp[i][j]=dp[i−1][j−1]
                if(word1[i-1]==word2[j-1]) dp[i][j]=dp[i-1][j-1];  
                //不相等情况一：删word1[i - 1]，最少操作次数为dp[i-1][j] + 1
                //不相等情况二：删word2[j - 1]，最少操作次数为dp[i][j-1] + 1
                //不相等情况三：同时删除，操作的最少次数为dp[i-1][j-1] + 2  。注意此处是 +2
                //else dp[i][j]=min({dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+2});  //3个数相比，需要加大括号
                //求最小,就一定不会是情况三
                else dp[i][j]=min(dp[i-1][j],dp[i][j-1]) +1;
            }
        }
        return dp[len1][len2];
    }
};

• 时间复杂度：O(mn)，其中 m 和 n 分别是字符串 word1 和 word2 的长度。二维数组 dp 有 m+1 行和 n+1 列，需要对 dp 中的每个元素进行计算。
• 空间复杂度：O(mn)，其中 m 和 n 分别是字符串 word1​ 和 word2​ 的长度。创建了 m+1 行 n+1 列的二维数组 dp。

解法2:动态规划(最长公共子序列)

思路:给定两个字符串 word1​ 和 word2​，分别删除若干字符之后使得两个字符串相同，则剩下的字符为两个字符串的公共子序列。为了使删除操作的次数最少，剩下的字符应尽可能多。当剩下的字符为两个字符串的最长公共子序列时，删除操作的次数最少。因此，可以计算两个字符串的最长公共子序列的长度，然后分别计算两个字符串的长度和最长公共子序列的长度之差，即为两个字符串分别需要删除的字符数，两个字符串各自需要删除的字符数之和即为最少的删除操作的总次数。

class Solution {
public:
    int minDistance(string word1, string word2) {
        int len1=word1.length(),len2=word2.length();
        vector> dp(len1+1,vector(len2+1,0)); 
        for(int i=1;i<=len1;++i){
            for(int j=1;j<=len2;++j){
                if(word1[i-1]==word2[j-1]){
                    dp[i][j] = dp[i-1][j-1] + 1 ;
                }else {
                    dp[i][j] = max( dp[i][j-1] , dp[i-1][j] ) ;  //特别注意不相等的情况
                }
            }
        }
        return len1+len2-2*dp[len1][len2];
    }
};

• 时间复杂度：O(mn)，其中 m 和 n 分别是字符串 word1 和 wprd2 的长度。二维数组 dp 有 m+1 行和 n+1 列，需要对 dp 中的每个元素进行计算。
• 空间复杂度：O(mn)，其中 m 和 n 分别是字符串 word1​ 和 word2​ 的长度。创建了 m+1 行 n+1 列的二维数组 dp。

43.*编辑距离

 

解法1:动态规划

思路:    dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离

class Solution {
public:
    int minDistance(string word1, string word2) {
         int len1=word1.length(),len2=word2.length();
         vector> dp(len1+1,vector(len2+1));
         for(int i=0;i<=len1;++i) dp[i][0]=i;    //必须带有  =
         for(int j=0;j<=len2;++j) dp[0][j]=j;
         for(int i=1;i<=len1;++i){
             for(int j=1;j<=len2;++j){
                 if(word1[i-1]==word2[j-1])   dp[i][j]=dp[i-1][j-1];
                 //1、插入与删除操作等价：word2插入一个元素，相当于word1删除一个元素
                 //   word1删除一个元素，那么就是以下标i-2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 + 一个删除操作
                 //   即 dp[i][j] = dp[i - 1][j] + 1;
                 //   同理：word2 删除一个元素，dp[i][j]=dp[i][j-1]+1
                 //2、替换：word1替换word1[i - 1]，使其与word2[j - 1]相同，此时不用增加元素，
                 //   以下标i-2为结尾的word1 与 j-2为结尾的word2的最近编辑距离 + 一个替换的操作
                 //   即，dp[i][j]=dp[i-1][j-1]+1
                 else dp[i][j]=min({dp[i-1][j],dp[i][j-1],dp[i-1][j-1]}) + 1;
             }
         }
         return dp[len1][len2];
    }
};

• 时间复杂度：O(mn)，其中 m 和 n 分别是字符串 word1 和 word2 的长度。二维数组 dp 有 m+1 行和 n+1 列，需要对 dp 中的每个元素进行计算。
• 空间复杂度：O(mn)，其中 m 和 n 分别是字符串 word1​ 和 word2​ 的长度。创建了 m+1 行 n+1 列的二维数组 dp。

44.*回文子串

 

 解法1:双指针

class Solution {
public:
    int countSubstrings(string s) {
        int ans=0;
        for(int i=0;i=0 && j

• 时间复杂度：O(n^2)，其中  n 是字符串 s  的长度。枚举回文中心的是 O(n) 的，对于每个回文中心拓展的次数也是 O(n) 的，所以时间复杂度是 O(n^2)。
• 空间复杂度：O(1)。

解法2:动态规划

class Solution {
public:
    //dp[i][j]：(bool类型) 表示区间范围[i,j]的子串是否是回文子串，如果是dp[i][j]为true，否则为false
    int countSubstrings(string s) {
        //此处定义为 bool类型，而且大小不 +1， 初始化为false, 因为 s[i]!=s[j] 一定不是回文串
         vector> dp(s.size(),vector(s.size(),false));
         int ans=0;
         //从递推公式中可以看出，根据dp[i + 1][j - 1]对dp[i][j]进行赋值true的
         //dp[i + 1][j - 1] 在 dp[i][j]的左下角, 故选择从下到上，从左到右的遍历顺序。dp[i][j] 的定义一定是j>i
         for(int i=s.size()-1;i>=0;--i){
             for(int j=i;j  dp[i][j] 为true
                 //j-i>1  : 例如cabac，此时s[i]与s[j]已经相同，我们看i到j区间是不是回文子串就看aba是不是回文，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
                 if(s[i]==s[j] && (j-i<=1 || dp[i+1][j-1])){
                     dp[i][j]=true;
                     ans++;
                 }
             }
         }
         return ans;
    }
};

class Solution {
public:
    int countSubstrings(string s) {
         vector> dp(s.size(),vector(s.size(),false));
         int ans=0;
         for(int i=s.size()-1;i>=0;--i){
             for(int j=i;j

• 时间复杂度：O(n^2)。
• 空间复杂度：O(n^2)。

45.*最长回文子串

 

解法1:双指针

class Solution {
public:
    string longestPalindrome(string s) {
        int len=s.length();
        for(int i=0;i=0 && jmaxlen){
                begin=i;
                maxlen=j-i+1;
            }
            --i;
            ++j;
        }
    }
    int begin=0,maxlen=0;
};

• 时间复杂度：O(n^2)，其中  n 是字符串 s  的长度。枚举回文中心的是 O(n) 的，对于每个回文中心拓展的次数也是 O(n) 的，所以时间复杂度是 O(n^2)。
• 空间复杂度：O(1)。

解法2:动态规划

class Solution {
public:
    string longestPalindrome(string s) {
         int len=s.length();
         int left=0,maxlen=0;
         vector> dp(len,vector(len,false));
         for(int i=len-1;i>=0;--i){
             for(int j=i;jmaxlen){
                     left=i;
                     maxlen=j-i+1;
                 }
             }
         }
         return s.substr(left,maxlen);
    }
};

• 时间复杂度：O(n^2)，其中 n 是字符串的长度。动态规划的状态总数为 O(n^2)，对于每个状态，我们需要转移的时间为 O(1)。
• 空间复杂度：O(n^2)，即存储动态规划状态需要的空间。

46.分割回文串 II

 解法1：动态规划

class Solution {
public:
    int minCut(string s) {
        int len=s.size();
        //判断是否为回文串
         vector> gg(len,vector(len,false));
         for(int i=len-1;i>=0;--i){
             for(int j=i;j dp(len,INT_MAX);
         for(int i=0;i

• 时间复杂度：O(n^2)，其中 n 是字符串的长度。动态规划的状态总数为 O(n^2)，对于每个状态，我们需要转移的时间为 O(1)。
• 空间复杂度：O(n^2)，即存储动态规划状态需要的空间。

47.最长回文子序列

 解法1:动态规划

思路: 回文子串是要连续的，回文子序列可不是连续的

class Solution { 
public:
    int longestPalindromeSubseq(string s) {
        int len=s.length();
        vector> dp(len,vector(len,0));  //没有 +1
        //由于任何长度为 1 的子序列都是回文子序列，因此对任意 0≤i=0;--i){
            for(int j=i+1;j

• 时间复杂度：O(n^2)，其中 n 是字符串 s 的长度。动态规划需要计算的状态数是 O(n^2)。
• 空间复杂度：O(n^2)，其中 n 是字符串 s 的长度。需要创建二维数组 dp，空间是 O(n^2)。

48.*正则表达式匹配

 解法1：动态规划

 思路：f[i][j] 表示 s 的前 i个字符与 p 中的前 j 个字符是否能够匹配。

（1）必须将 a* 看成一个整体进行匹配 ！！！！a* 中a 如果不匹配，还要看后面有没有跟着*，*的出现可以把a干掉，即出现了0次a 。 （2） .*  可以与任意两个字符匹配。

主要分三种情况：情况1：未进行任何匹配，对应 f[0][0] 。情况2：使用了 p 中的一些字符，但没有匹配 s（也就是出现 * 的情况），对应 f[0][>0] 。情况3：使用了 p 中的一些字符且匹配了 s 的一些字符，对应 f[>0][>0]    。不存在「没有使用 p 中的字符，但匹配了 s 的一些字符」这种情况 

class Solution {
private:
    bool match(string &s,string &p,int i,int j){
        if(i==0) return false;     // s 为空，p不为空
        //只有当 p[j-1]='.' 或 s[i-1]=p[j-1] 才会匹配
        if(p[j-1]=='.') return true;  //'.'是万能的，一定可以匹配上
        return s[i-1]==p[j-1]; 
    }
public:
    bool isMatch(string s, string p) {
        int m=s.length(),n=p.length();
        vector> dp(m+1,vector(n+1));
        dp[0][0]=true;
        for(int i=0;i<=m;++i){    // i从0开始，j从1开始 （且必须得带等号）
            for(int j=1;j<=n;++j){  //j=0 表示p为空串
                if(p[j-1]=='*'){   
                    //s[i]=p[j-1] : 可以选择匹配，或者不匹配，就浪费一个 '*'
                    //dp[i-1][j]匹配 s 末尾的一个字符，将该字符扔掉，而该组合还可以继续进行匹配；dp[i][j-2]不匹配
                    dp[i][j] = match(s,p,i,j-1) ? (dp[i-1][j] or dp[i][j-2]) : dp[i][j-2];
                }
                else{
                    //如果 p 的第 j 个字符是一个小写字母，那么我们必须在 s 中匹配一个相同的小写字母
                    dp[i][j] = match(s,p,i,j) ? dp[i-1][j-1] : false;
                }
            }
        }
        return dp[m][n];
    }
};

• 时间复杂度：O(mn)，其中 m 和 n 分别是字符串 s 和 p 的长度。我们需要计算出所有的状态，并且每个状态在进行转移时的时间复杂度为 O(1)。
• 空间复杂度：O(mn)，即为存储所有状态使用的空间。

49.*乘积最大子数组

解法1：动态规划

class Solution {    //动态规划
public:
    //maxDp[i]：第 i 个元素结尾的乘积最大子数组的乘积
    //minDp[i]：第 i 个元素结尾的乘积最小子数组的乘积
    int maxProduct(vector& nums) {
        int n=nums.size(),ans=nums[0];
        vector maxDp(n),minDp(n);
        maxDp[0]=minDp[0]=nums[0];    //初始化
        for(int i=1;i

• 时间复杂度：O(n)。
• 空间复杂度：O(n)。

解法2：动态规划（优化空间）

class Solution {    //动态规划
public:
    //maxDp[i]：第 i 个元素结尾的乘积最大子数组的乘积
    //minDp[i]：第 i 个元素结尾的乘积最小子数组的乘积
    int maxProduct(vector& nums) {
        int n=nums.size();
        int maxDp=nums[0],minDp=nums[0],ans=nums[0];
        for(int i=1;i

• 时间复杂度：O(n)。
• 空间复杂度：O(1)，优化后只使用常数个临时变量作为辅助空间，与 n 无关。

50.统计全为1的正方形子矩阵

解法1：动态规划

思路：f[i][j] 表示以 (i, j) 为右下角的正方形的最大边长，那么除此定义之外，f[i][j] = x 也表示以 (i, j) 为右下角的正方形的数目为 x（即边长为 1, 2, ..., x 的正方形各一个）。在计算出所有的 f[i][j] 后，我们将它们进行累加，就可以得到矩阵中正方形的数目。

class Solution {
public:
    int countSquares(vector>& matrix) {
        int row=matrix.size(),col=matrix[0].size();
        if(!row || !col) return 0;
        vector> dp(row,vector(col));
        int ans=0;
        for(int i=0;i

• 时间复杂度：O(mn)。
• 空间复杂度：O(mn)，由于递推式中 f[i][j] 只与本行和上一行的若干个值有关，因此空间复杂度可以优化至 O(n)。

51.*最大正方形

 解法1：动态规划

思路：动态规划：先求边长，再求面积。dp[i][j]表示以 (i, j) 为右下角(以元素为角)，且只包含 1 的正方形的 边长 最大值。如果该位置的值是 1，则 dp(i,j) 的值由其上方、左方和左上方的三个相邻位置的 dp 值决定。

class Solution {    
public:
    int maximalSquare(vector>& matrix) {
        int row=matrix.size(),col=matrix[0].size();
        if( !row || col==0) return 0;
        int ans=0;
        vector> dp(row,vector(col));
        for(int i=0;i

• 时间复杂度：O(mn)，其中 m 和 n 是矩阵的行数和列数。需要遍历原始矩阵中的每个元素计算 dp 的值。
• 空间复杂度：O(mn)，其中 m 和 n 是矩阵的行数和列数。创建了一个和原始矩阵大小相同的矩阵 dp。由于状态转移方程中的 dp(i,j) 由其上方、左方和左上方的三个相邻位置的 dp 值决定，因此可以使用两个一维数组进行状态转移，空间复杂度优化至 O(n)。

52.*戳气球

 解法1：动态规划

反向思维：戳气球的操作会导致两个气球从不相邻变成相邻，使得后续操作难以处理。于是我们倒过来看这些操作，将全过程看作是每次添加一个气球。问题转化为在开区间 (i,j) 中添加气球。开区间：因为不能和已经计算过的产⽣联系，我们这样定义之后，利⽤两个虚拟⽓球（第一个和最后一个为1） 就可完成本题。

（1）当 i≥j−1 时，开区间中没有气球，solve(i,j) 的值为 0；（2）当 i

class Solution {     //是典型的枚举分割点 DP  
public:
    int maxCoins(vector& nums) {
        int n=nums.size();
        vector> dp(n+2,vector(n+2));
        vector val(n+2);
        val[0]=val[n+1]=1;  //初始化添加的最前和最后的两个虚拟指针为 1
        for(int i=1;i<=n;++i){
            val[i]=nums[i-1];  //重要
        }       
        //「自底向上」的动态规划
        for(int i=n-1;i>=0;--i){
            for(int j=i+2;j<=n+1;++j){
                for(int k=i+1;k

• 时间复杂度：O(n^3)，其中 n 是气球数量。状态数为 n^2，状态转移复杂度为 O(n)，最终复杂度为 O(n^2×n)=O(n^3)。
• 空间复杂度：O(n^2)，其中 n 是气球数量。

解法2：记忆化搜索

class Solution {     
private:
    int solve(int left,int right){
        if(left>=right-1){
            return 0;
        }
        if(re[left][right]!=-1){
            return re[left][right];
        }       
        for(int i=left+1;i> re;
    vector val;  
public:
    int maxCoins(vector& nums) {
        int len=nums.size();
        val.resize(len+2);  //前后分别加了一个数，防止越界
        for(int i=1;i<=len;++i){
            val[i]=nums[i-1];  //重要
        }
        val[0]=val[len+1]=1;  //初始化添加的最前和最后的两个虚拟指针为 1
        re.resize(len+2,vector(len+2,-1));
        return solve(0,len+1);
    }
};

53.丑数

 

 

 解法1：数学

 思路：当 n>0 时，若 n 是丑数，则 n 可以写成 n= 2^a × 3^b × 5^c 的形式，其中 a,b,c 都是非负整数。特别地，当 a,b,c 都是 0 时，n=1。为判断 n 是否满足上述形式，可以对 n 反复除以 2,3,5直到 n 不再包含质因数 2,3,5。若剩下的数等于 1，则说明 n 不包含其他质因数，是丑数；否则，说明 n 包含其他质因数，不是丑数。

class Solution {
public:
    bool isUgly(int n) {
        if(n<=0) return false; //0 和负整数一定不是丑数
        vector factors={2,3,5};
        for(int factor:factors){
            while(n%factor==0){
                n/=factor;
            }
        }
        return n==1;
    }
};

• 时间复杂度：O(logn)，时间复杂度取决于对 n 除以 2,3,5 的次数，由于每次至少将 n 除以 2，因此除法运算的次数不会超过 O(log⁡n)。
• 空间复杂度：O(1)。

54.丑数II

 

 解法1：动态规划

思路：丑数只包含因子 2,3,5，因此有 “丑数 = 某较小丑数 × 某因子”

每轮计算 dp[i] 后，需要更新索引 p2,p3,p5 的值，使其始终满足方程条件。实现方法：分别独立判断 dp[i] 和 dp[p2]×2 , dp[p3]×3 , dp[p5]×5 的大小关系，若相等则将对应索引 p2,p3,p5 加 1；

class Solution {
public:
    int nthUglyNumber(int n) {
        int p2=0,p3=0,p5=0;
        vector dp(n);
        dp[0]=1;
        for(int i=1;i

• 时间复杂度：O(n)，需要计算数组 dp 中的 n 个元素，每个元素的计算都可以在 O(1) 的时间内完成。
• 空间复杂度：O(n)，空间复杂度主要取决于数组 dp 的大小。

55.#丑数

 

 解法1：动态规划

class Solution {
public:
    int nthUglyNumber(int n) {
        int p2=0,p3=0,p5=0;
        vector dp(n);
        dp[0]=1;
        for(int i=1;i

56.超级丑数

 解法1：动态规划

class Solution {
public:
    int nthSuperUglyNumber(int n, vector& primes) {
        int m = primes.size();
        vector p(m, 0);
        vector dp(n);
        dp[0]=1;
        for (int i = 1; i < n; ++i) {
            long minNum = INT_MAX;
            for (int j = 0; j < m; j++) {
                minNum = min(minNum, dp[p[j]] * primes[j]);
            }
            dp[i] = minNum;
            for (int j = 0; j < m; ++j) {
                if (dp[i] == dp[p[j]] * primes[j])  p[j]++;
            }
        }
        return dp[n-1];
    }
};

• 时间复杂度：O(nm)，其中 n 是待求的超级丑数的编号，m 是数组 primes 的长度。需要计算数组 dp 中的 n 个元素，每个元素的计算都需要 O(m) 的时间。
• 空间复杂度：O(n+m)，其中 n 是待求的超级丑数的编号，m 是数组 primes 的长度。需要创建数组 dp、数组 p，空间分别是 O(n) 和 O(m) 。

57、小红取数

 解法1：动态规划

#include
using namespace std;
// dp[i][j]表示前i个数截止，余数为j的最大和
long long maxSum(vector nums, long long k){
    int len=nums.size();
    vector> dp(len+1,vector(k,LONG_LONG_MIN));
    dp[0][0]=0;
    for(int i=1; i<=len; ++i){
        for(int j=0;j>n>>k;
     vector vec(n);   // 必须指定数组长度后，才能使用for循环 cin>>vec[i]
     for(int i=0;i>vec[i];
     }
     cout<

58、背包最多能装多大价值的物品（未装满+恰好装满）

 解法1：完全背包

#include
using namespace std;
int main(){
    int n,V;
    cin >> n >> V;
    vector v(n+1),w(n+1);
    for (int i=0; i>v[i]>>w[i];
    }
    
    vector dp1(V+1,0);
    for (int i=0; i dp2(V+1,INT_MIN);
    dp2[0] = 0;
    for (int i=0; i

59、鸡蛋掉落

 解法1：动态规划+二分查找

class Solution {
public:
    int superEggDrop(int k, int n) {
        // 要与原来的dp比较求小的值,必定要初始化为最大值才不会对第一个值大的比较产生影响
        vector> dp(n+1,vector(k+1,INT_MAX));
        // 初始化i=0,1与j=0,1
        // j=0时,鸡蛋数目为0:操作数怎样都是0(无法操作)
        // j=1时,鸡蛋数目为1:当楼层数n>=1时候为n
        for(int i = 1; i <= n; i++) {
            dp[i][0] = 0;
            dp[i][1] = i;
        }
        dp[0][1] = 0;
        // i=0时,楼层数目为0:操作数怎样都是0(无法上楼)
        for(int j = 0; j <= k; j++) {
            dp[0][j] = 0;
        }
        // i=1时,楼层数目为1:当鸡蛋数k>=1时候为1,只需要扔一次即可
        for(int j = 1; j <= k; j++) {
            dp[1][j] = 1;
        }

        // 之后遍历范围为i∈[2,n],j∈[2,k]
        for(int i = 2; i <= n; i++) {
            for(int j = 2; j <= k; j++) {
                // 通过二分法在区间[1,i]确定一个最优值
                int left = 1, right = i;
                // 这里用二分查找k∈[1,i]中最小的那个dp(k)->一个v形函数
                // 最低点在中间,可以通过二分在O(logn)时间复杂度内找到最小的k值
                while(left < right) {
                    // 这里的mid是偏右的,因此右边主动-1往左收缩
                    int mid = left + (right - left + 1) / 2;
                    // 碎了，就需要往低层继续扔：层数少 1 ，鸡蛋也少 1
                    // 不碎，就需要往高层继续扔：层数是当前层到最高层的距离差，鸡蛋数量不少
                    // 两种情况都做了一次尝试，所以加 1
                    int breakCount = dp[mid - 1][j - 1];    // 递增
                    int notBreakCount = dp[i - mid][j];     // 递减
                    // 排除法（减治思想），先想什么时候不是解
                    // 严格大于的时候一定不是解，此时 mid 一定不是解
                    // 下一轮搜索区间是 [left, mid - 1]                    
                    if(breakCount > notBreakCount) {
                        right = mid - 1;
                    }else {
                        // 这个区间一定是上一个区间的反面，即 [mid, right]
                        left = mid;
                    }
                }
                // left == right时退出循环,这个下标就是最优的 k 
                // 把它代入转移方程 max(dp[k - 1][j - 1], dp[i - k][j]) + 1) 即可
                dp[i][j] = max(dp[left - 1][j - 1], dp[i - left][j] + 1);
            }
        }
        return dp[n][k];
    }
};

• 时间复杂度：O(knlogn)。我们需要计算 O(kn) 个状态，每个状态计算时需要 O(log⁡n) 的时间进行二分查找。
• 空间复杂度：O(kn)。我们需要 O(kn) 的空间存储每个状态的解。

60.猜数字大小II

解法1：动态规划

为了将支付的金额最小化，除了需要将每次支付的金额控制在较低值以外，还需要在猜数字的过程中缩小所选数字的范围。

class Solution {
public:
    int getMoneyAmount(int n) {
        vector> dp(n+1,vector(n+1));
        for(int i=1;i=1;--i){
            for(int j=i+1;j<=n;++j){
                dp[i][j]=dp[i][j-1]+j;  //为了避免出现下标越界:当j=n时，如果k=j则 k+1>n，此时 f[k][j]会出现下标越界。
                for(int k=i;k