数据结构：基本概念【详解】

友情链接：数据结构专栏

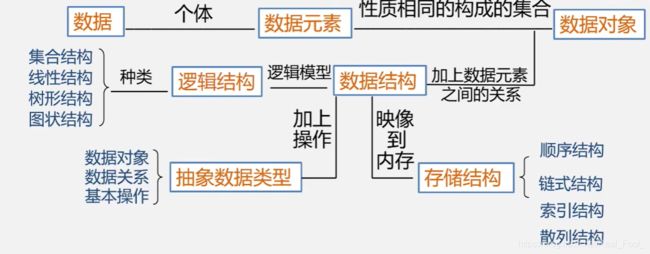
知识框架

数据结构是一门研究非数值计算的程序设计问题中的操作对象，以及它们之间的关系的操作等相关问题的学科

程序设计=数据结构+算法

---

No.1 什么是数据结构？

一、基本概念和术语

1.数据

数据：是描述客观事物的符号，是计算机中可以操作的对象，是能被计算机识别，并输入给计算机处理的符号集合。（数据不仅包含整型、实型等数值类型，还包括字符及声音、图像、视频等非数值类型。）

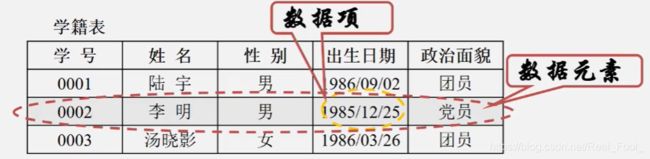
2.数据元素

数据元素：是组成数据的、有一定意义的基本单位，在计算机中通常作为整体处理。也被成为记录。（比如：鸡鸭牛羊猪狗等动物就是禽类的数据元素）

3.数据项

数据项：一个数据元素可以由若干个数据项组成。（比如：人可以有眼耳口鼻这些数据项）。
数据项是数据不可分割的最小单位。

4.数据对象

数据对象：是性质相同的数据元素的集合，是数据的子集。（什么是性质相同呢，是指数据元素具有相同数量和类型的数据项，比如：人都有姓名、生日、性别等相同的数据项）
既然数据对象是数据的子集，在实际应用中，处理的数据元素通常具有相同性质，在不产生混淆的情况下，我们都将数据对象简称为数据。

5.数据结构

不同的数据元素之间不是独立的，而是存在特定的关系，我们将这些关系成为结构。
数据结构：是相互之间存在一种或多种特定关系的数据元素的集合。

二、逻辑结构和物理结构

1.逻辑结构

逻辑结构：是指数据对象中数据元素之间的相互关系。

集合结构
集合结构：集合结构中的数据元素除了同属于一个集合外，他们之间没有其他关系。

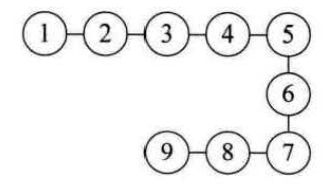
线性结构
线性结构：线性结构中的数据元素之间是一对一的关系

树形结构
树形结构：树形结构中的数据元素之间存在一种一对多的层次关系。

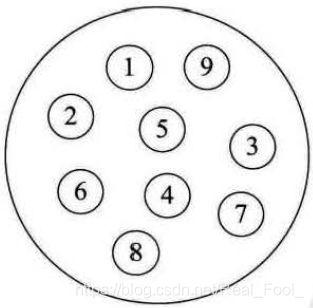
图形结构
图形结构：图形结构的数据元素是多对多的关系

2.物理结构（存储结构）

物理结构：是指数据的逻辑结构在计算机中的存储形式。
数据元素的存储结构形式有两种：顺序存储和链式存储。
顺序存储结构
顺序存储结构：是把数据存放在地址连续的存储单元里，其数据间的逻辑关系和物理关系是一致的。

链式存储结构
链式存储结构：是把数据元素存放在任意的存储单元里，这组存储单元可以是连续的，也可以是不连续的。数据元素的存储关系并不能反映其逻辑关系，因此需要用一个指针存放数据元素的地址，这样通过地址就可以找到相关联数据元素的位置。

三、抽象数据类型

1.数据类型

数据类型：是指一组性质相同的值的集合及定义在此集合上的一些操作的总称。
不同的数据类型，开辟出的内存空间也不一样。
在C语言中，按照取值的不同，数据类型可以分为两类：

• 原子类型：是不可再分解的基本类型，包括整型、实型、字符型。
• 结构类型：由若干个类型组合而成，是可以再分解的。例如，整型数组是由若干个整型数据组成的。

比如，在C语言中变量生命int a，b，这就意味着，在给变量a和b赋值时不能超出int的取值范围，变量a和b之间的运算只能是int类型所允许的运算。

2.抽象数据类型

抽象是指抽取事物具有的普遍性的本质。
**抽象数据类型（Abstract Data Type, ADT）：是指一个数学模型及定义在改模型上的一组操作。**抽象数据类型的定义仅取决于它的一组逻辑特性，而与其他计算机内部如何表示和实现无关。抽象数据类型体现了程序设计中的问题分解、抽象和信息隐藏的特性。

---

No.2 算法

一、算法定义

算法是解决特定问题求解步骤的描述，在计算机中表现为指令的有限序列，并且每条指令表示一个或多个操作。

二、算法特性

算法具有五个基本特性：输入、输出、有穷性、确定性和可行性。
算法的设计要求：正确性、可读性、健壮性、高效率和低存储量需求。
算法的度量方法：事后统计方法（不科学、不准确）、事前分析估算方法。

三、函数的渐进增长

函数的渐进增长：给定两个函数f(n)和g(n)，如果存在一个整数N，使得对于所有的n > N，f(n)总是比g(n)大，那么，我们说f(n)的增长渐进快于g(n)。

判断一个算法效率时，函数中的常熟和其他次要项常常可以忽略，而更应该关注主项（最高阶项）的阶数。

判断一个算法好不好，我们只通过少量的数据是不能做出准确的判断的。如果我们可以对比某些算法的关键执行次数函数的渐进增长性，基本就可以分析出：某个算法，随着n的增大，它会越来越优于另一算法，或者越来越差于另一算法。

四、算法时间复杂度

1.算法时间复杂度定义

在进行算法分析时，语句总的执行次数T(n)是关于问题规模n的函数，进而分析T(n)随n的变化情况并确定T(n)的数量级。
算法的时间复杂度，也就是算法的时间度量，记作：$$T(n)=O(f(n))$$。他表示随问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐进时间复杂度，简称为时间复杂度。其中f(n)是问题规模n的某个函数。

这样用大写O()来体现算法时间复杂度的记法，我们称之为大O记法。
一般情况下，随着n的增大，T(n)增长最慢的算法为最优算法。

常见的时间复杂度

执行次数函数举例	阶	非正式术语
12	O(1)	常数阶
2n+3	O(n)	线性阶
3n2+2n+1	O(n2)	平方阶
5log2n+20	O(logn)	对数阶
2n+3nlog2n+19	O(nlogn)	nlogn阶
6n3+2n2+3n+4	O(n3)	立方阶
2n	O(2n)	指数阶

所消耗的时间从小到大的比较：

$$O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)$$

2.推导大O阶方法

推导大O阶

1. 用常数1取代运行时间中的所有加法常数。
2. 在修改后的运行次数函数中，只保留最高阶项。
3. 如果最高阶项存在且不是1，则去除与这个项相乘的常数。
   得到的结果就是大O阶。

3.最坏情况和平均情况

我们查找一个有n个随机数字数组的某个数字，最好的情况是第一个数字就是，那么算法的时间复杂度为O(1)，但也有可能这个数字就在最后一个位置上待着，那么算法的时间复杂度就是O(n)，这就是最坏的一种情况了。
最坏情况运行时间是一种保证，那就是运行时间将不会再坏了。在应用中，这是一种最重要的需求，通常，除非特别指定，我们提到的运行时间都是最坏情况的运行时间。

4.算法空间复杂度

算法的空间复杂度通过计算算法所需的存储空间实现，算法空间复杂度的计算公式记作：$$S(n)=O(f(n))$$其中，n为问题的规模，f(n)为语句关于n所占存储空间的函数。

附录

下文链接

数据结构：线性表

专栏

数据结构专栏

参考资料

1、严蔚敏、吴伟民：《数据结构（C语言版）》
2、程杰：《大话数据结构》
3、王道论坛：《数据结构考研复习指导》
4、托马斯·科尔曼等人：《算法导论》