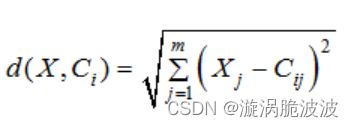k-means聚类算法学习笔记(案例分析、python代码,结果可视化)
文章目录
- 1 什么是k-means聚类
- 2 案例分析(计算过程)
- 3 python代码
- 4 结果可视化
1 什么是k-means聚类
K-Means算法是一种典型的基于划分的聚类算法,也是一种无监督学习算法。K-Means算法的思想很简单,对给定的样本集,用欧氏距离作为衡量数据对象间相似度的指标,相似度与数据对象间的距离成反比,相似度越大,距离越小。
预先指定初始聚类数以及个初始聚类中心,按照样本之间的距离大小,把样本集划分为个簇根据数据对象与聚类中心之间的相似度,不断更新聚类中心的位置,不断降低类簇的误差平方和(Sum of Squared Error,SSE),当SSE不再变化或目标函数收敛时,聚类结束,得到最终结果。
K-Means算法的核心思想:首先从数据集中随机选取k个初始聚类中心Ci(i≤1≤k),计算其余数据对象与与聚类中心Ci的欧氏距离,找出离目标数据对象最近的聚类中心Ci,并将数据对象分配到聚类中心Ci所对应的簇中。然后计算每个簇中数据对象的平均值作为新的聚类中心,进行下一次迭代,直到聚类中心不再变化或达到最大的迭代次数时停止。
2 案例分析(计算过程)
将如下8个点(用(x,y)代表位置)聚类为3个类:X1(2,10)、X2(2,5)、X3(8,4)、X4(5,8)、X5(7,5)、X6(6,4)、X7(1,2)、X8(4,9),距离计算方式采用欧几里德距离。假设初始化时选择X1、X4、X7为每个聚类的中心,用K-means算法对8个点进行聚类。
第一轮迭代过程如下:计算出各点到中心点的欧氏距离(此处用平方值简略代表),计算出新一轮的中心点坐标。

第二轮迭代,计算各点到新中心点的距离,计算出新的中心点

由以上方法同理得出:
第三轮聚类中心节点坐标为:(3.67,9),(7,4.33),(1,2.33)
第四轮聚类中心节点坐标为:(3.67,9),(1.5,3.5),(7,4.33)
第三次和第四次中心节点坐标结果一致,表明聚类无需在聚,聚类结果为:{X1,X3,X8} ,{X2,X7},{X3,X5,X6}
3 python代码
import random
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 计算欧式距离
def Distance(dataSet, centroids, k) -> np.array:
dis = []
for data in dataSet:
diff = np.tile(data, (k, 1)) - centroids # 行数上复制k份,方便作差
temp1 = diff ** 2
temp2 = np.sum(temp1, axis=1) # 按行相加
dis_temp = temp2 ** 0.5
dis.append(dis_temp)
dis = np.array(dis) # 转换为一个array类型
#print(dis)
return dis
# 更新质心
def Update_cen(dataSet, centroids, k):
# 计算每个样本到质心的距离,返回值是array数组
distance = Distance(dataSet, centroids, k)
# print("输出所有样本到质心的距离:", distance)
# 分组并计算新的质心
minIndex = np.argmin(distance, axis=1) # axis=1 返回每行最小值的索引
# print("输出最小值索引", minIndex)
newCentroids = pd.DataFrame(dataSet).groupby(minIndex).mean()
# print("新的质心(dataframe):", newCentroids)
newCentroids = newCentroids.values
# print("新的质心(值):", newCentroids)
# 计算变化量
changed = newCentroids - centroids
return changed, newCentroids
# k-means 算法实现
def kmeans(dataSet, k):
# (1) 随机选定k个质心
#centroids = random.sample(dataSet, k)
centroids=[[2,10],[5,8],[1,2]]
print("随机选定两个质心:", centroids)
# (2) 计算样本值到质心之间的距离,直到质心的位置不再改变
changed, newCentroids = Update_cen(dataSet, centroids, k)
while np.any(changed):
changed, newCentroids = Update_cen(dataSet, newCentroids, k)
centroids = sorted(newCentroids.tolist())
# (3) 根据最终的质心,计算每个集群的样本
cluster = []
dis = Distance(dataSet, centroids, k) # 调用欧拉距离
minIndex = np.argmin(dis, axis=1)
for i in range(k):
cluster.append([])
for i, j in enumerate(minIndex): # enumerate()可同时遍历索引和遍历元素
cluster[j].append(dataSet[i])
return centroids, cluster
# 创建数据集
def createDataSet():
return [[2,10],[2,5],[8,4],[5,8],[7,5],[6,4],[1,2],[4,9]]
if __name__ == '__main__':
dataset = createDataSet() # type(dataset)='list'
centroids, cluster = kmeans(dataset, 3) # 2 代表的是分为2类=2个质心
print('质心为:%s' % centroids)
print('集群为:%s' % cluster)
# x = list(np.array(dataset).T[0])
# y = list(np.array(dataset).T[1])
plt.scatter(list(np.array(dataset).T[0]), list(np.array(dataset).T[1]), marker='o', color='green', label="数据集" )
plt.scatter(list(np.array(centroids).T[0]), list(np.array(centroids).T[1]), marker='x', color='red', label="质心")
plt.show()
运行结果:
随机选定两个质心: [[2, 10], [5, 8], [1, 2]]
质心为:[[1.5, 3.5], [3.6666666666666665, 9.0], [7.0, 4.333333333333333]]
集群为:[[[2, 5], [1, 2]], [[2, 10], [5, 8], [4, 9]], [[8, 4], [7, 5], [6, 4]]]
4 结果可视化
代码跑出来可视化聚类结果为:
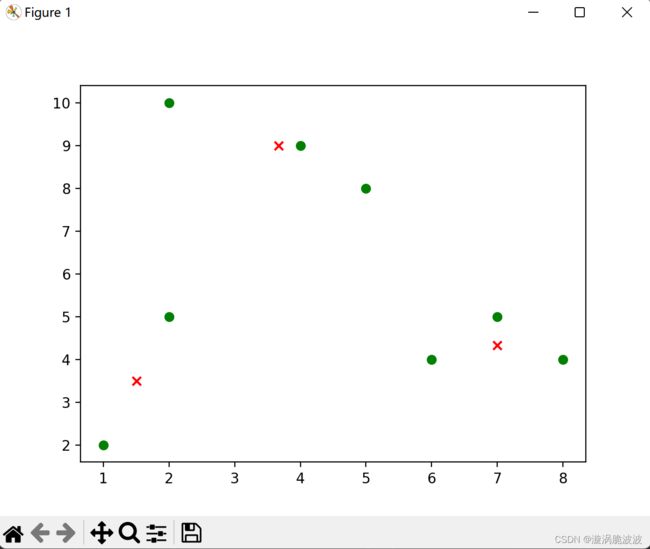
可能不太明显,是因为数据太少了,不过主要是为了了解该算法的原理,在接下来的学习中便于进一步探索。