最近公共祖先问题

最近公共祖先问题

1.在将最近公共祖先问题之前，先来回顾一个简单算法：

给你输入一棵没有重复元素的二叉树根节点root和一个目标值val，请你写一个函数寻找树中值为val的节点。

这道题有以下三种解法：

// 定义：在以 root 为根的二叉树中寻找值为 val 的节点
TreeNode find(TreeNode root, int val) {
    // base case
    if (root == null) {
        return null;
    }
    // 看看 root.val 是不是要找的
    if (root.val == val) {
        return root;
    }
    // root 不是目标节点，那就去左子树找
    TreeNode left = find(root.left, val);
    if (left != null) {
        return left;
    }
    // 左子树找不着，那就去右子树找
    TreeNode right = find(root.right, val);
    if (right != null) {
        return right;
    }
    // 实在找不到了
    return null;
}

二叉树的前序遍历：

但是这段代码的实际运行效率会低一些，因为如果在左子树能找到目标节点就没有必要去右子树寻找了。但是这段代码还是会去右子树找一圈所以效率会相对差一些

TreeNode find(TreeNode root, int val) {
    if (root == null) {
        return null;
    }
    // 前序位置
    if (root.val == val) {
        return root;
    }
    // root 不是目标节点，去左右子树寻找
    TreeNode left = find(root.left, val);
    TreeNode right = find(root.right, val);
    // 看看哪边找到了
    return left != null ? left : right;
}

二叉树的后序遍历：

在这里利用后序遍历效率会进一步下降，因为在后序位置判断，就算根节点就是目标节点也要先去左右子树遍历完所有节点才能判断出来。而前序遍历，只要找到了目标值就可以停止搜索。

TreeNode find(TreeNode root, int val) {
    if (root == null) {
        return null;
    }
    // 先去左右子树寻找
    TreeNode left = find(root.left, val);
    TreeNode right = find(root.right, val);
    // 后序位置，看看 root 是不是目标节点
    if (root.val == val) {
        return root;
    }
    // root 不是目标节点，再去看看哪边的子树找到了
    return left != null ? left : right;
}

2.基于上一题的基础，对题目进行修改

寻找值为val1或val2的节点

这道题和上一道题的实现基本一致

// 定义：在以 root 为根的二叉树中寻找值为 val1 或 val2 的节点
TreeNode find(TreeNode root, int val1, int val2) {
    // base case
    if (root == null) {
        return null;
    }
    // 前序位置，看看 root 是不是目标值
    if (root.val == val1 || root.val == val2) {
        return root;
    }
    // 去左右子树寻找
    TreeNode left = find(root.left, val1, val2);
    TreeNode right = find(root.right, val1, val2);
    // 后序位置，已经知道左右子树是否存在目标值

    return left != null ? left : right;
}

而最近公共祖先系列问题的解法都是基于这个代码框架的

3.最近公共祖先系列问题

3.1 236. 二叉树的最近公共祖先

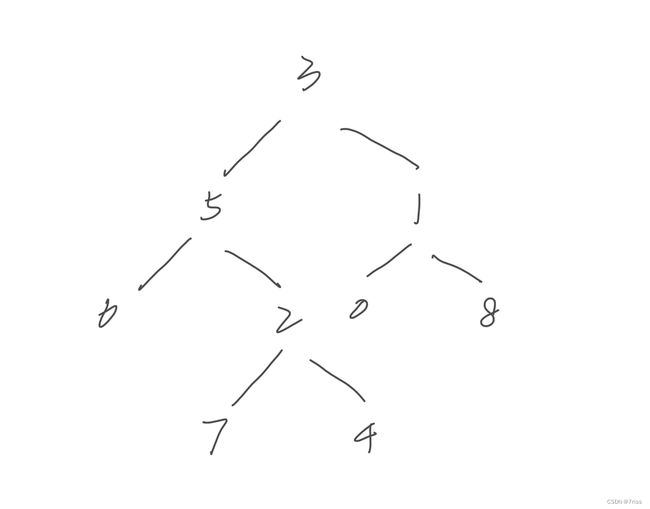
这道题就是给你输入一棵不含重复值的二叉树，以及存在于树中的两个节点p和q，请你计算p和q的最近公共祖先节点。

对于最近公共祖先，有以下两种情况：

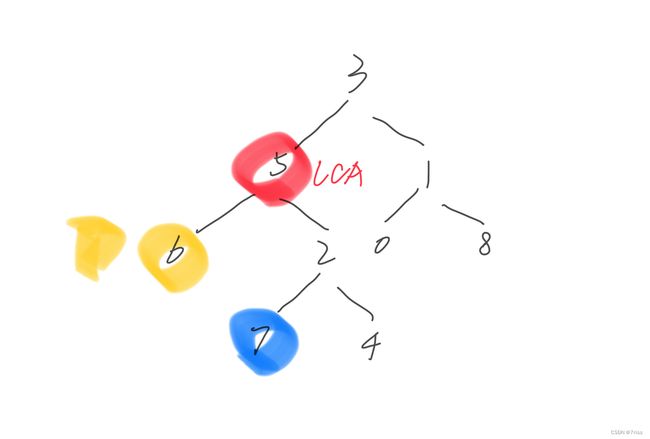
• 情况1：如果p是节点6，q是节点7，那么它俩的LCA就是节点5

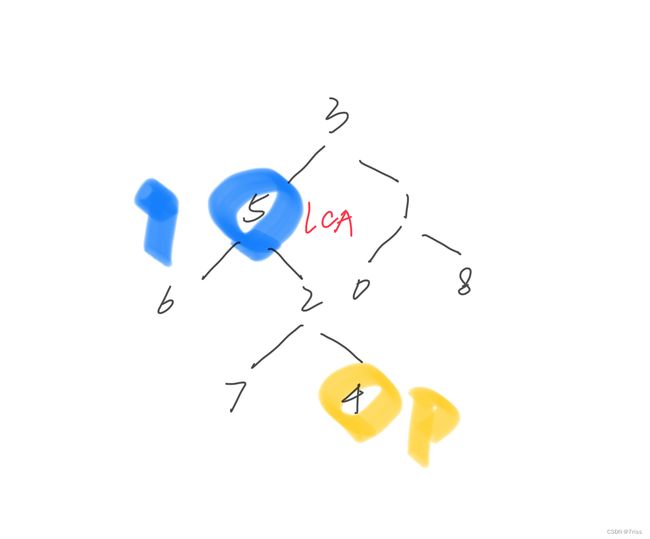
• 情况2：p和q本身也可能是LCA，比如这种情况q本身就是LCA节点

对以上两种情况进行总结：两个节点的最近公共祖先其实就是这两个节点向根节点的「延长线」的交汇点

那对于任意一个节点，它如何知道自己是不是p和q的最近公共祖先？（情况1）

答：如果一个节点能够在它的左右子树中分别找到p和q，则该节点为LCA节点

而根据这个说明是先到左右子树中寻找，也就是说我们可以用到的是后序位置，在后序位置判断当前节点的左右子树是否为空，都不为空，则该节点为LCA节点。

那对于任意一个节点，它如何知道自己是不是p或q并且是最近公共祖先？（情况2）

答：其实这个 很容易解决，如果当前节点是p或q说明他就是最近公告最先，那就直接返回当前节点，否则就遍历他的左右子树。显然这是在前序位置完成逻辑判断。

那为什么只要遇到p或者q就直接返回呢？这是因为题目说了p和q一定存在于二叉树中，所以只要遇到p就说明q在p的下面，那么p就是LCA节点。

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        return find(root,p,q);
    }
    public TreeNode find(TreeNode root,TreeNode p,TreeNode q){
        if(root==null) return null;
        if(root==p||root==q){
            return root;
        }
        TreeNode left=find(root.left,p,q);
        TreeNode right=find(root.right,p,q);
        if(left!=null&&right!=null){
            return root;
        }
        return left!=null?left:right;
    }

3.2 1676二叉树的最近公共祖先 IV

依然给你输入一棵不含重复值的二叉树，但这次不是给你输入p和q两个节点了，而是给你输入一个包含若干节点的列表nodes（这些节点都存在于二叉树中），让你算这些节点的最近公共祖先。

这道题的解题框架是一样的，只是有点细节不一样

TreeNode lowestCommonAncestor(TreeNode root, TreeNode[] nodes) {
    // 将列表转化成哈希集合，便于判断元素是否存在
    HashSet<Integer> values = new HashSet<>();
    for (TreeNode node : nodes) {
        values.add(node.val);
    }
    return find(root, values);
}

// 在二叉树中寻找 values 的最近公共祖先节点
TreeNode find(TreeNode root, HashSet<Integer> values) {
    if (root == null) {
        return null;
    }
    // 前序位置
    if (values.contains(root.val)){
        return root;
    }

    TreeNode left = find(root.left, values);
    TreeNode right = find(root.right, values);
    // 后序位置，已经知道左右子树是否存在目标值
    if (left != null && right != null) {
        // 当前节点是 LCA 节点
        return root;
    }
    return left != null ? left : right;
}

3.3 1644二叉树的最近公共祖先 II

给你输入一棵不含重复值的二叉树的，以及两个节点p和q，如果p或q不存在于树中，则返回空指针，否则的话返回p和q的最近公共祖先节点。

在解决标准的最近公共祖先问题时，我们在find函数的前序位置有这样一段代码：

// 前序位置
if (root.val == val1 || root.val == val2) {
    // 如果遇到目标值，直接返回
    return root;
}

因为p和q都存在于树中，所以这段代码恰好可以解决最近公共祖先的第二种情况。

但是对于这道题来说，p和q不一定存在于树中，所以你不能遇到一个目标值就直接返回，而应该对二叉树进行完全搜索（遍历每一个节点），如果发现p或q不存在于树中，那么是不存在LCA的。

而在前面分析的几种find函数的写法，哪种写法能够对二叉树进行完全搜索来着？

TreeNode find(TreeNode root, int val) {
    if (root == null) {
        return null;
    }
    // 先去左右子树寻找
    TreeNode left = find(root.left, val);
    TreeNode right = find(root.right, val);
    // 后序位置，判断 root 是不是目标节点
    if (root.val == val) {
        return root;
    }
    // root 不是目标节点，再去看看哪边的子树找到了
    return left != null ? left : right;
}

答案是在后序位置进行逻辑判断

所以代码实现如下：

// 用于记录 p 和 q 是否存在于二叉树中
boolean foundP = false, foundQ = false;

TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    TreeNode res = find(root, p.val, q.val);
    if (!foundP || !foundQ) {
        return null;
    }
    // p 和 q 都存在二叉树中，才有公共祖先
    return res;
}

// 在二叉树中寻找 val1 和 val2 的最近公共祖先节点
TreeNode find(TreeNode root, int val1, int val2) {
    if (root == null) {
        return null;
    }
    TreeNode left = find(root.left, val1, val2);
    TreeNode right = find(root.right, val1, val2);

    // 后序位置，判断当前节点是不是 LCA 节点
    if (left != null && right != null) {
        return root;
    }

    // 后序位置，判断当前节点是不是目标值
    if (root.val == val1 || root.val == val2) {
        // 找到了，记录一下
        if (root.val == val1) foundP = true;
        if (root.val == val2) foundQ = true;
        return root;
    }

    return left != null ? left : right;
}

这样改造，对二叉树进行完全搜索，同时记录p和q是否同时存在树中，从而满足题目的要求。

3.4 1650二叉树的最近公共祖先 III

这次输入的二叉树节点比较特殊，包含指向父节点的指针：

class Node {
    int val;
    Node left;
    Node right;
    Node parent;
};

由于节点中包含父节点的指针，所以二叉树的根节点就没必要输入了。

这道题其实不是公共祖先的问题，而是单链表相交的问题，你把parent指针想象成单链表的next指针，题目就变成了：

给你输入两个单链表的头结点p和q，这两个单链表必然会相交，请你返回相交点。

Node lowestCommonAncestor(Node p, Node q) {
    // 施展链表双指针技巧
    Node a = p, b = q;
    while (a != b) {
        // a 走一步，如果走到根节点，转到 q 节点
        if (a == null) a = q;
        else           a = a.parent;
        // b 走一步，如果走到根节点，转到 p 节点
        if (b == null) b = p;
        else           b = b.parent;
    }
    return a;
}

4.二叉搜索树的最近公共祖先

235. 二叉搜索树的最近公共祖先

给你输入一棵不含重复值的二叉搜索树，以及存在于树中的两个节点p和q，请你计算p和q的最近公共祖先节点。

这道题显然可以用之前我们在二叉树中寻找最近公共祖先，但是没有用到BST左小右大，显然效率是不高的。

在标准的最近公共祖先问题中，我们要在后序位置通过左右子树的搜索结果来判断当前节点是不是LCA：

TreeNode left = find(root.left, val1, val2);
TreeNode right = find(root.right, val1, val2);

// 后序位置，判断当前节点是不是 LCA 节点
if (left != null && right != null) {
    return root;
}

但是对于 BST 来说，根本不需要老老实实去遍历子树，由于 BST 左小右大的性质，将当前节点的值与val1和val2作对比即可判断当前节点是不是LCA：

假设val1 < val2，那么val1 <= root.val <= val2则说明当前节点就是LCA；若root.val比val1还小，则需要去值更大的右子树寻找LCA；若root.val比val2还大，则需要去值更小的左子树寻找LCA。

TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    // 保证 val1 较小，val2 较大
    int val1 = Math.min(p.val, q.val);
    int val2 = Math.max(p.val, q.val);
    return find(root, val1, val2);
}

// 在 BST 中寻找 val1 和 val2 的最近公共祖先节点
TreeNode find(TreeNode root, int val1, int val2) {
    if (root == null) {
        return null;
    }
    if (root.val > val2) {
        // 当前节点太大，去左子树找
        return find(root.left, val1, val2);
    }
    if (root.val < val1) {
        // 当前节点太小，去右子树找
        return find(root.right, val1, val2);
    }
    // val1 <= root.val <= val2
    // 则当前节点就是最近公共祖先
    return root;
}