代码随想录Day36
今天继续学习贪心算法解决相关问题
134.加油站
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。
思路:
1.最初想到的是借助双重for循环,外层遍历整个数组作为起始位置的判断,内层遍历是否能完整跑完一圈。那么借助贪心的思路进一步想一想,如果所有的油量加起来比总消耗量少,那么一定不可能跑完全程;如果要跑完全程那么总油量加起来一定要比总消耗量大,那么每一个站点的gas[i] - cost[i]全部加起来后应当是≥0的。
2.本题实质上和之前找最大子序和的思路有些类似,子序和中一旦当前连续和小于0就舍弃当前连续和,从下一个位置开始重新记录;而本题中的连续和实质上就是连续的gas[i] - cost[i]之和,而一旦当前位置的gas[i] - cost[i]小于0说明我们到达不了下一个站点了,此时应当从下一个站点重新作为开始位置进行模拟。
class Solution {
public:
int canCompleteCircuit(vector& gas, vector& cost) {
int totalSum = 0;//计算总的加油量减消耗量
int curSum = 0;//计算当前跑过的路线里的加油量减消耗量
int start = 0;//记录开始的位置
for(int i = 0; i < gas.size(); i++){
totalSum += gas[i] - cost[i];
curSum += gas[i] - cost[i];
//curSum < 0说明开不到下一站了,之前选择的开始位置无效,从下一个位置重新作为开始位置
if(curSum < 0){
start = i + 1;
curSum = 0;
}
}
//遍历完毕后如果totalSum < 0,说明总的加油量小于总的消耗量,无论如何都不可能存在解
if(totalSum < 0) return -1;
return start;
}
}; 启发:
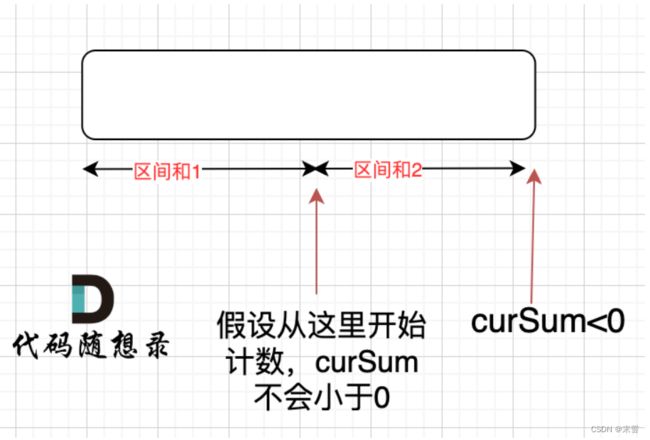
1.在做本题时有产生疑问,如果当前位置的curSum < 0,那我从前面一段路的中间再选一个开始位置,到达当前位置会不会让curSum > 0?
假设我们将前一段路的中间从选择的新的开始位置拆成两段road1和road2,由于当前位置的curSum < 0,那么可以保证road1和road2的curSum相加一定小于0,又因为目前我们假设的从新的开始位置到目前位置的curSum > 0,即road2的curSum > 0,那么前半段路road1的curSum一定小于0,实质上依旧是在当前的curSum < 0后选择了下一个位置作为新的开始位置。
(此处引用代码随想录中的讲解原图)
2.本题也是通过一个变量记录总油量减总消耗量,一个变量记录当前位置的剩余量以做到将双层的循环优化为单层循环,在这种思路上需要进一步理解。
135.分发糖果
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求,给这些孩子分发糖果:
每个孩子至少分配到 1 个糖果。
相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
示例 1:
输入:ratings = [1,0,2]
输出:5
解释:你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。
示例 2:
输入:ratings = [1,2,2]
输出:4
解释:你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果,这满足题面中的两个条件。
思路:
1.根据题目,我们可以将增加糖果的数目分为两种情况:(1)当前孩子比左边孩子分数高,(2)当前孩子比右边孩子分数高。
2.分别根据以上两种情况遍历两次数组,当满足情况的条件时就在分数较低的那个孩子的糖果数量基础上加一个糖果就是当前孩子的糖果数量。至于为什么要将两种情况区分开,一个是因为同时兼顾两种情况会很复杂,一个是因为当我们先遍历完一种情况后,另一个情况遍历时需要用到前一种情况遍历后的结果。
class Solution {
public:
int candy(vector& ratings) {
int result = 0;
vector candys(ratings.size(), 1);
//先找当前孩子比左边孩子分高的情况
for(int i = 1; i < ratings.size(); i++){
if(ratings[i] > ratings[i - 1]){
candys[i] = candys[i - 1] + 1;
}
}
//再找当前孩子比右边孩子分高的情况
for(int i = candys.size() - 2; i >= 0; i--){
if(ratings[i] > ratings[i + 1]){
//注意要取最大值,因为先前已经找过了比左边孩子分高的情况
candys[i] = max(candys[i + 1] + 1, candys[i]);
}
}
for(int i = 0; i < candys.size(); i++){
result += candys[i];
}
return result;
}
}; 启发:
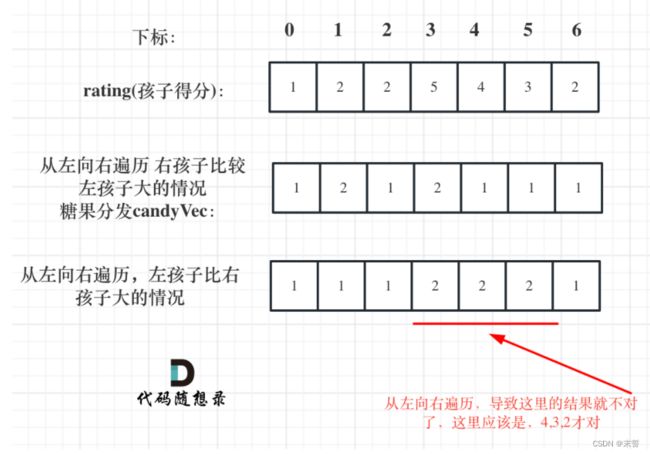
1.本题中的遍历顺序也非常有讲究,在确定当前孩子比右孩子分数高的情况时一定要从后向前遍历。我们假设要比较的时下标为0,1,2的三个孩子,且0>1>2,如果从前向后遍历,那么下标为0和下标为1的孩子都只会分得两个糖果,这里问题就显示出来了:下标为0的孩子并不满足比下标为1的孩子糖果数量多一个。因为下标为0的孩子与下标为1的孩子的结果要取决于下标为1的孩子与下标为2的孩子的结果情况;从后向前遍历的时候,先比较了1和2,此时1的糖果个数为2,再比较0和1,0的糖果数量为3,这样才满足了题目的要求。
(此处引用代码随想录中的讲解原图)
2.在对第二种情况进行遍历时一定要对糖果数量取最大值,只有取最大值才能在与右边孩子和左边孩子的糖果数量比较时同时满足题目的要求。