((蓝桥杯 刷题全集)【备战(蓝桥杯)算法竞赛-第6天(动态规划 专题)】( 从头开始重新做题,记录备战竞赛路上的每一道题 )距离蓝桥杯还有61天
欢迎观看我的博客,如有问题交流,欢迎评论区留言,一定尽快回复!(大家可以去看我的专栏,是所有文章的目录)
文章字体风格:
红色文字表示:重难点✔★
蓝色文字表示:思路以及想法✔★
如果大家觉得有帮助的话,感谢大家帮忙
点赞!收藏!转发!
我的qq号是:1210931886,欢迎大家加群,一起学习,互相交流,共同进步✨✨
蓝桥杯系列,为大家提供
- 做题全集,备战蓝桥杯,就做这个系列的题即可
- 一个大概的做题规划——大家最好在此基础上提前两个月准备
备战蓝桥杯就刷这些题
第一天博客链接 - 基础算法 -上
第二天博客链接 - 基础算法 -下 + 数据结构专题
第三天博客链接 - 搜索与图论-上 专题
第四天博客链接 - 搜索与图论-下 专题
第五天博客链接 - 数学知识专题
第六天博客链接 - 动态规划 专题
第七天博客链接 - 贪心算法 专题
蓝桥杯 刷题全集
- 一、背包问题
-
-
-
-
- ★f[i][j] 背包容量为j,前i个物品的最大价值
- 1. 01背包问题(不需要初始化) ✔1.6 ✔1.7
- 2. 完全背包问题 ✔1.6
-
-
- 一、朴素做法
- 二、二维数组的优化(需要判断j是否大于v[i])
- 三、一维数组的优化
-
- 3. 多重背包问题 I ✔1.6
- 4. 多重背包问题 II ✔1.6
-
-
- s 分解成 哪些数 可以加和表示 1-s
-
- 5. 分组背包问题 ✔1.6
-
-
-
- 二、线性DP
-
-
-
- 1. 数字三角形 ✔1.6
- 2. 最长上升子序列
-
-
- ★双重循环(子序列不一定连续)
-
- 3. 最长上升子序列 II ✔1.6
-
-
- ★f[i] 存储 最长上升子序列的 示范串
- ★ 二分 + dp优化
-
- 4. 最长公共子序列 ✔1.6
-
-
- ★f[i][j]表示a的前i个字母,和b的前j个字母的最长公共子序列长度
- 思路 (在推导示例时,可以总结出)
-
- 5. 最短编辑距离 ✔1.6
-
-
- ★f[i][j] 所有把a中的前i个字母 变成 b中前j个字母的集合的操作集合
- 做题总结:f[i-1][j] 到 f的距离 和 f[i][j-1] 到f的距离差很远
-
- 6. 编辑距离
-
-
- ★f[i][j] 所有把a中的前i个字母 变成 b中前j个字母的集合的操作集合
-
-
-
- 三、区间dp
-
-
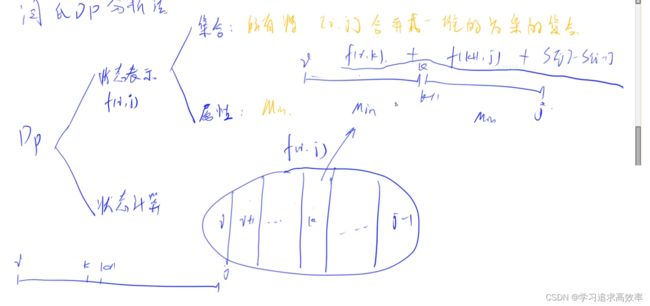
- 1. 石子合并
-
- ★f[i][j]表示将 i 到 j 合并的最小值
-
-
- 区间dp的套路
-
-
- 四、计数类DP
-
-
- ★1. 整数划分
-
- ★f[i][j] 表示 背包为j的 前i个物品 的方案数
-
- f[i][0] 是1
-
一、背包问题
★f[i][j] 背包容量为j,前i个物品的最大价值
1. 01背包问题(不需要初始化) ✔1.6 ✔1.7
原题链接
f[i][j]怎么想出来
在j体积下 前i个物品的最大价值
一、为什么要从0到v把背包中各种体积下的情况都存储下来呢?(算法理解)
因为我们需要回溯
二、但我们选i的时候,需要明白两件事
选不选第i件物品的判断依据
- 当 背包中限定的体积,小于v【i】一定不能选
- 当 背包中限定的体积可以装下v[i]时,那么我们就需要知道,到底装下这个价值大,还是不装下这个价值大
装下的价值 = f[i-1][j-v[i]] + w[i]
不装下的价值 = f[i-1][j];
总结:深刻记住 f[i][j] 表示 在j体积中前i个物品下的最大价值
二维
#include一维
#include 2. 完全背包问题 ✔1.6
一、朴素做法
#include二、二维数组的优化(需要判断j是否大于v[i])
#include三、一维数组的优化
#include二维
#include一维
#include怎么由二维变成一维
看更新f[i][j] 需要的是本行数据还是上行数据
3. 多重背包问题 I ✔1.6
原题链接
三重循环(针对的是f[i][j]处理)
★不需要处理j不够的情况
#include4. 多重背包问题 II ✔1.6
s 分解成 哪些数 可以加和表示 1-s
原题链接
#include5. 分组背包问题 ✔1.6
原题链接
二维
#include一维
#include 二、线性DP
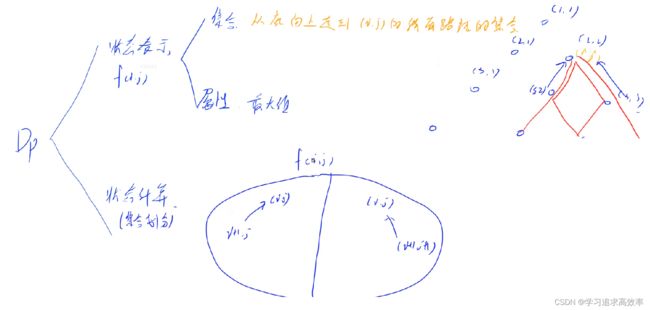
1. 数字三角形 ✔1.6
★f[i][j] 从下到上 走到f[i][j]的所有路径的最大值
原题链接
原题链接
#include2. 最长上升子序列
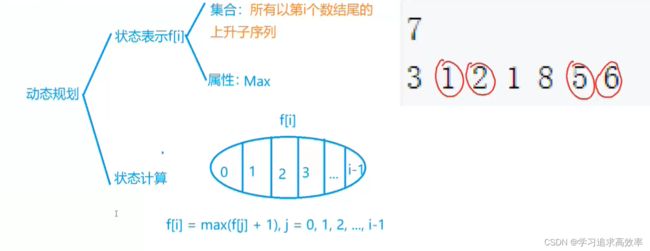
★双重循环(子序列不一定连续)
★f[i] 以第i个数结尾的 上升子序列的最大值
原题链接
原题链接
#include3. 最长上升子序列 II ✔1.6
★f[i] 存储 最长上升子序列的 示范串
★ 二分 + dp优化
原题链接
#include4. 最长公共子序列 ✔1.6
★f[i][j]表示a的前i个字母,和b的前j个字母的最长公共子序列长度
原题链接
思路 (在推导示例时,可以总结出)
- f[i][j] 表示什么需要先想清楚。
表示的是:在i,j组合的情况下,的最大子串 长度
所以当 i,j相等时
f[i][j] = f[i-1][j-1] + 1
不相等的时候
f[i][j] = max(f[i-1][j],f[i][j-1]);
#include5. 最短编辑距离 ✔1.6
原题链接
★f[i][j] 所有把a中的前i个字母 变成 b中前j个字母的集合的操作集合
做题总结:f[i-1][j] 到 f的距离 和 f[i][j-1] 到f的距离差很远
#include 6. 编辑距离
★f[i][j] 所有把a中的前i个字母 变成 b中前j个字母的集合的操作集合
原题链接
三、区间dp
- 遍历区间长度值
- 遍历左端点
得到右端点 - 遍历左右端点之间的值
1. 石子合并
★f[i][j]表示将 i 到 j 合并的最小值
区间dp的套路
- 先遍历区间长度
- 遍历区间左端点,由左端点+区间长度 找到右端点
本题
- 求f[i][j] 是求从i到j 中取哪个k值使得总和最小,
所以要遍历i到j中的 每个值(用k遍历)
#include 四、计数类DP
题解
★1. 整数划分
★f[i][j] 表示 背包为j的 前i个物品 的方案数
f[i][0] 是1
#include