java实现归并排序(详解)
主要思想
归并排序和快速排序都是基于分而治之的算法思想。
归并排序先将待排序的数组不断拆分,直到拆分到区间里只剩下一个元素的时候。不能再拆分的时候。这个时候我们再想办法合并两个有序的数组,得到长度更长的有序数组。当前合并好的有序数组为下一轮得到更长的有序数组做好了准备。一层一层的合并回去,直到整个数组有序。
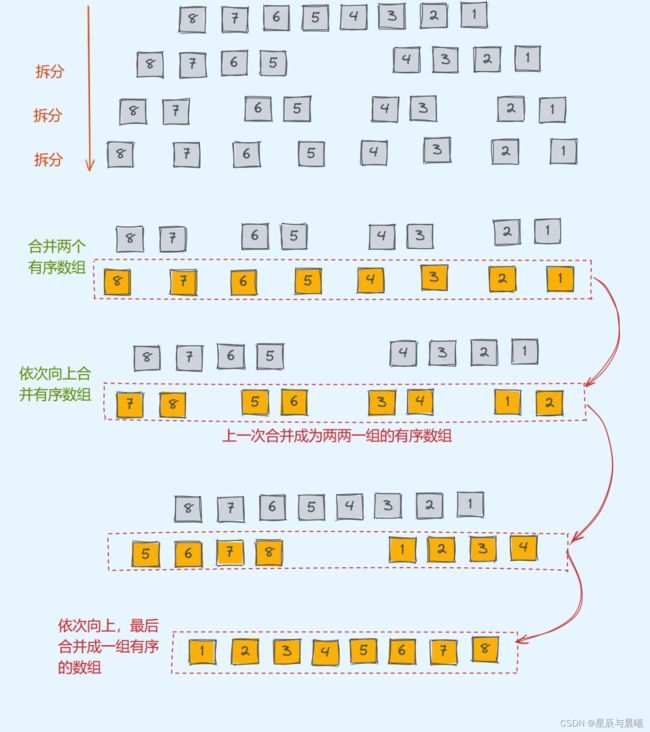
在这各整个过程当中,不停做的事情就是拆分问题和组合子问题的解,在这里很显然我们是需要使用递归来实现归并排序。
如何合并两个有序数组
在这里我们是一个一个的选出来的。
先选出两个数组里最小的元素,然后再选出两个数组中第二小的元素,因为两个数组都是有序的,所以两个数组里的最小的元素肯定是出现在两个数组的开头。
所以我们只需要比较两个数组中开头的两个元素,较小的那一个就是两个数组中最小的那一个,我们就将它拿出来放到一个新的地方,接着选出两个元素中第二小的元素,依然是比较这个时候两个数组开头的两个元素,谁较小,谁就是数组中第二小的,依次向下进行。
直到将所有的元素选择出来,我们就把两个有序的数组成功合并为一个更长的有序数组。
在我们实际应用的时候,两个有序数组是两个紧挨着的两个有序空间。
在使用的时候,我们先把原始数组要合并的部分复制到一个新的区域,然后在复制出来的辅助数组上设置两个下标 i 和 j ,分别指向两个有序区间的第一个元素,然后再在输入数组上设置一个变量k用于赋值。
首先比较 i 和 j 所指向的元素,我把就把小的数赋值为k,然后向后移动下标。
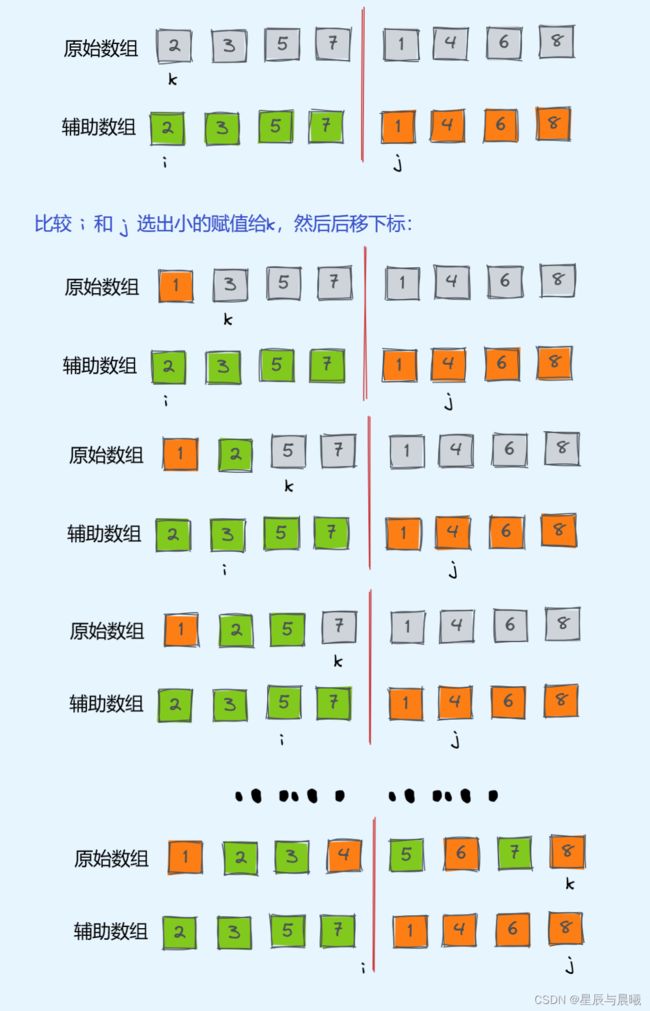
这也是个典型的空间换时间的一种做法。
在开始时那为了演示,使用的是同时拆分同时合并的,但在归并排序当中,实际使用的是按照深度优先的顺序完成归并排序的。
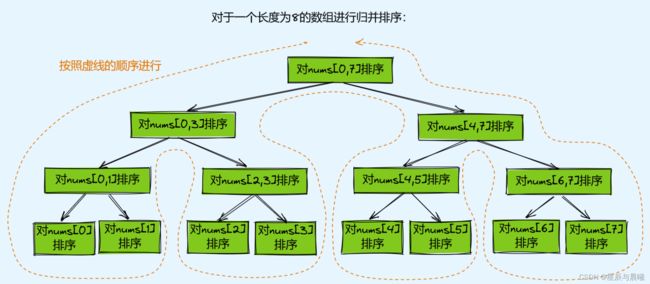
按照深度优先的顺序进行:
0 ~ 7分为0 ~ 3和4 ~ 7两组;
然后0 ~ 3分为0 ~ 1和2 ~ 3两组;
然后0 ~ 1分为 0和1;
再然后0和1整理为有序数组;
再又对2 ~ 3分为 2 和 3;
对2 和3 进行整理为有序数组;
再将 0 ~ 1和2 ~ 3进行整理为有序数组;
再对 4 ~ 7分为 4 ~ 5和 6 ~ 7两组;
。。。。。
最后整理成为有序数组。
深度优先遍历只要可以继续拆分问题,就先拆分问题;直到只有一个元素时不能拆分的时候,才回到之前它走过的地方走另一条还没有走过的路径继续走下去。直到走完所有的可能走的路径。因此称为深度优先遍历
代码实现:
import java.util.Arrays;
public class Demo912_2 {
public static void main(String[] args) {
int[] nums = {-1, 2, -8, -10}; //给定一个数组
int[] after = sortArray(nums); //的带排序后的数组
System.out.println(Arrays.toString(after)); //打印输出得到数组
}
private static int[] sortArray(int[] nums) {
int len = nums.length;
int[] temp = new int[len];
mergeSort(nums,0,len-1,temp);
return nums;
}
/**
* 递归函数对nums[left...right]进行归并排序
* @param nums 原数组
* @param left 左边的索引
* @param right 右边记录索引位置
* @param temp
*/
private static void mergeSort(int[] nums, int left, int right, int[] temp) {
if (left == right){//当拆分到数组当中只要一个值的时候,结束递归
return;
}
int mid = (left+right)/2; //找到下次要拆分的中间值
mergeSort(nums,left,mid,temp);//记录树左边的
mergeSort(nums,mid+1,right,temp);//记录树右边的
//合并两个区间
for (int i = left; i <= right; i++) {
temp[i] = nums[i];
//temp就是辅助列表,新列表的需要排序的值就是从辅助列表中拿到的
}
int i = left; //给辅助数组里面的值标点
int j = mid +1;
for (int k = left; k <= right ; k++) {//k 就为当前要插入的位置
if (i == mid + 1){
nums[k] = temp[j];
j++;
}else if (j == right+1){
nums[k] = temp[i];
i++;
}
else if (temp[i] <= temp[j]){
nums[k] = temp[i];
i++;
}else {
nums[k] = temp[j];
j++;
}
}
}
}
对于复杂度分析来讲,可以忽略这个常数项,而且对数的底我们也不在乎。
所以我们最终的时间复杂度为:

归并排序的优化
第一个优化:
可以在小区间内使用插入排序。就是在判断当left == right这里使用一个区间的插入排序,当数组长度较小的时候,使用插入排序。
在这里我们将这个值设置为16。当数组的长度小于16的时候,就使用插入排序,提高代码执行效率。

第二个优化:
就是在合并两个有序的数组之前,我们先看看这两个数组拼接起来,是不是已经成为了有序的数组。

最终代码:
归并排序后两种优化结束后的最终代码:
import java.util.Arrays;
public class Demo912_2 {
public static void main(String[] args) {
int[] nums = {-1, 2, -8, -10}; //给定一个数组
int[] after = sortArray(nums); //的带排序后的数组
System.out.println(Arrays.toString(after)); //打印输出得到数组
}
private static int[] sortArray(int[] nums) {
int len = nums.length;
int[] temp = new int[len];
mergeSort(nums, 0, len - 1, temp);
return nums;
}
/**
* 递归函数对nums[left...right]进行归并排序
*
* @param nums 原数组
* @param left 左边的索引
* @param right 右边记录索引位置
* @param temp
*/
private static void mergeSort(int[] nums, int left, int right, int[] temp) {
if (right - left < 16) {//当拆分到数组长度小于16的时候,直接插入排序来提高代码运行速度
insertionSort(nums, right, left);
return;
}
int mid = (left + right) / 2; //找到下次要拆分的中间值
mergeSort(nums, left, mid, temp);//记录树左边的
mergeSort(nums, mid + 1, right, temp);//记录树右边的
if (nums[mid] <= nums[mid + 1]) {
//因为整数除法是向下取整,所以这里不会代写mid + 1越界
return;
}
//合并两个区间
for (int i = left; i <= right; i++) {
temp[i] = nums[i]; //temp就是辅助列表,新列表的需要排序的值就是从辅助列表中拿到的
}
int i = left; //给辅助数组里面的值标点
int j = mid + 1;
for (int k = left; k <= right; k++) {//k 就为当前要插入的位置
if (i == mid + 1) {
nums[k] = temp[j];
j++;
} else if (j == right + 1) {
nums[k] = temp[i];
i++;
} else if (temp[i] <= temp[j]) {
nums[k] = temp[i];
i++;
} else {
nums[k] = temp[j];
j++;
}
}
}
/**
* 执行插入排序
* @param nums
* @param right
* @param left
*/
private static void insertionSort(int[] nums, int right, int left) {
for (int i = left + 1; i <= right; i++) {
int temp = nums[i];
int j;
for (j = i; j > left; j--) {
if (nums[j - 1] > temp) {
nums[j] = nums[j - 1];
} else {
break;
}
}
nums[j] = temp;
}
}
}
总结
归并排序采用的是分治算法。
分治算法每一次执行都可以分为三个步骤:
- 分解:把一个大问题拆成小问题;
- 解决:逐个解决小问题;
- 合并:再把这些小问题的结果组合起来组成大问题的解。
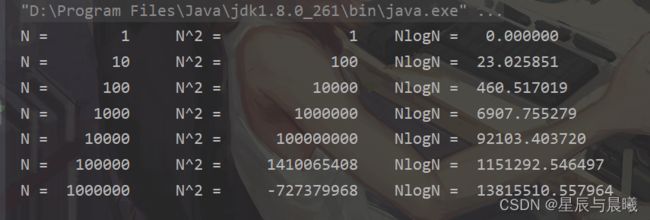
O(N logN)比O(N^2)快多少?
一段代码演示:
public class Demo {
public static void main(String[] args) {
for (int N = 1; N <= 100_0000; N *= 10) {
System.out.printf("N = % 8d", N);
System.out.printf("\t N^2 = % 14d", N*N);
System.out.printf("\t NlogN = % 10f", N * Math.log(N));
System.out.println();
}
}
}
我们这采用的是递归来实现归并排序,还有自底向上的归并排序和原地完成的归并排序。
在理论自底向上的归并排序是比采用递归快一丢丢的,但是考虑到学习成本来讲,就没必要了╰(●’◡’●)╮ ٩(๑′0`๑)۶
在上面的代码中,我们使用了 int mid = (left + right) / 2;来找出当前数组中的中间值.
在这里我们可以采用一个防止整型溢出的写法:
int mid = left +(right - left)/ 2;
也可以使用一个无符号右移的方式,理论上更快一点点:
int mid = left + (right - left) >> 1;
也可以直接写成:
int mid =(right - left) >> 1;
因为即使left +right会造成溢出,但右移以后,无符号的高位依然会补0,所以结论依然正确。
练习:
剑指offer 51. 数组中的逆序对
LeetCode315、计算右侧小于当前元素的个数