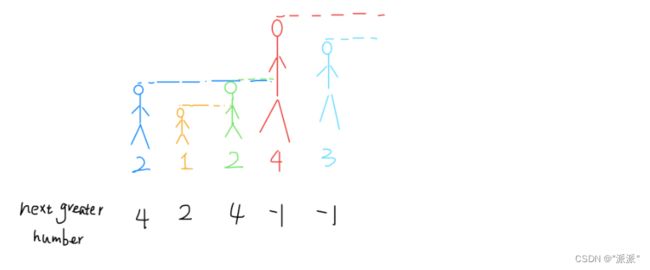单调栈入门详解
目录
基本概念
相关题型
下一个更大元素(力扣496)
接雨水(力扣42)
柱状图中最大的矩形(力扣84)
基本概念
概念:创建一个栈,使得每次新元素入栈后,栈内的元素都保持有序(单调递增或单调递减)。
举个例子看下:
给你一个数组,返回一个等长的数组,对应索引存储着下一个更大元素,如果没有更大的元素,就存 -1。
例如:输入数组[2,1,2,4,3],输出数组[4,2,4,-1,-1]。
解决方法:可以暴力遍历,时间复杂度较高O(n^2)。利用栈的特性,从后往前去遍历这个数组。题目意思是要返回对应位置的下一个更大元素,这个问题可以这样抽象思考:把数组的元素想象成并列站立的人,元素大小想象成人的身高。这些人面对你站成一列,如何求元素「2」的 Next Greater Number 呢?很简单,如果能够看到元素「2」,那么他后面可见的第一个人就是「2」的 Next Greater Number,因为比「2」小的元素身高不够,都被「2」挡住了,第一个露出来的就是答案。
具体思路:
从后往前遍历数组的元素,将这个元素(Cur)与栈顶(Din)的元素相比较(如栈为空,即设为-1),若当前元素小于栈顶元素,说明当前位置往后且比当前位置大的元素就是Din,设为Din,并将Cur入栈。若Cur大于Din,说明自己后面的元素(Din)都比自己小,将Din出栈,继续比较,最后也把Cur入栈。
代码编写:
vector nextGreaterElement(vector& nums) {
vector ans(nums.size()); // 存放答案的数组
stack s;
for (int i = nums.size() - 1; i >= 0; i--) { // 倒着往栈里放
while (!s.empty() && s.top() <= nums[i]) { // 判定个子高矮
s.pop(); // 矮个起开,反正也被挡着了。。。
}
ans[i] = s.empty() ? -1 : s.top(); // 这个元素身后的第一个高个
s.push(nums[i]); // 进队,接受之后的身高判定吧!
}
return ans;
}
补充:可以利用这个思路解决其它类似问题,例如:
给你一个数组 T = [73, 74, 75, 71, 69, 72, 76, 73],这个数组存放的是近几天的天气气温(这气温是铁板烧?不是的,这里用的华氏度)。你返回一个数组,计算:对于每一天,你还要至少等多少天才能等到一个更暖和的气温;如果等不到那一天,填 0 。
例题1:
给你 T = [73, 74, 75, 71, 69, 72, 76, 73],你返回 [1, 1, 4, 2, 1, 1, 0, 0]。
思路:与上一题完全一样,栈中存元素下标即可。
例题2:
思路:可以将原始数组“翻倍”,就是在后面再接一个原始数组,这样的话,按照之前“比身高”的流程,每个元素不仅可以比较自己右边的元素,而且也可以和左边的元素比较了。
代码:
vector nextGreaterElements(vector& nums) {
int n = nums.size();
vector res(n); // 存放结果
stack s;
// 假装这个数组长度翻倍了
for (int i = 2 * n - 1; i >= 0; i--) {
while (!s.empty() && s.top() <= nums[i % n])
s.pop();
res[i % n] = s.empty() ? -1 : s.top();
s.push(nums[i % n]);
}
return res;
}
以上代码思路图片来源链接:力扣
相关题型
下一个更大元素(力扣496)
题目描述:
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素
思路:同样是查找比自己大的下一个元素,只不过这题查找的元素是对应于另一个数组,在另一个数组进行查找。所以可以用哈希的思想,先对数组2操作,找到每个元素值(key)对应的下一个更大元素(value),再去遍历数组1,用建立好的映射关系直接查找即可。
代码:
class Solution {
public:
vector nextGreaterElement(vector& nums1, vector& nums2) {
stack s_;
unordered_map m_;
for(int i=nums2.size()-1;i>=0;i--)//遍历数组2
{
while(!s_.empty()&&s_.top()<=nums2[i])
{
s_.pop();
}
m_[nums2[i]]=s_.empty()?-1:s_.top();//找到数组2中下一个最大元素,用unordered_map
//建立映射关系
s_.push(nums2[i]);
}
vector nums3;
for(int i=0;i 接雨水(力扣42)
题目描述:给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
思路:暴力遍历,每次找到比当前元素(cur)左右的最大的元素(p1,p2)。min(p1,p2)-cur就是cur位置能接的雨水。时间杂度(n²)
优化:用两个数组,分别记录比当前左右位置最大元素,时间复杂度(n)。空间杂度(n)。
代码:
class Solution {
public:
int trap(vector& height) {
if (height.size() <= 2) return 0;
vector maxLeft(height.size(), 0);
vector maxRight(height.size(), 0);
int size = maxRight.size();
// 记录每个柱子左边柱子最大高度
maxLeft[0] = height[0];
for (int i = 1; i < size; i++) {
maxLeft[i] = max(height[i], maxLeft[i - 1]);
}
// 记录每个柱子右边柱子最大高度
maxRight[size - 1] = height[size - 1];
for (int i = size - 2; i >= 0; i--) {
maxRight[i] = max(height[i], maxRight[i + 1]);
}
// 求和
int sum = 0;
for (int i = 0; i < size; i++) {
int count = min(maxLeft[i], maxRight[i]) - height[i];//可认为宽度为1
if (count > 0) sum += count;
}
return sum;
}
}; 单调栈解法:
之前上面题型所用到的栈都是单调递增的,且是倒着遍历数组的。这题与之相反。
假设对应下标为 0 1 2 3 4
1.从前往后看,下标0--2,数组都是递减的,这就说明这样不可能存储到雨水。(用栈模拟:将下标为0-1-2的元素依次入栈,每次入栈时当前元素都小于栈顶元素)
2.当遍历到下标为3的元素时,它对应位置的元素大于前面那个元素,说明可以存储到雨水了。(用栈模拟:当前位置元素大于栈顶元素,将栈顶元素(cur)出栈(也就是下标为2的),同时记录其高度(元素大小),那么此时cur左右的元素都比它大,确定cur左右元素的较小值-cur高度就是雨水的高度,同时也能根据下标确定其宽度,那么就可以确定当前元素cur的雨水了)。
代码示例:
class Solution {
public:
int trap(vector& height) {
stack s_;
int count=0;
for(int i=0;i 柱状图中最大的矩形(力扣84)
题目描述:
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
解法1:暴力遍历,每次找到比当(cur)左右最小且最近的那个(p1,p2),说明以cur为基准,可以扩展到p1,p2,且为矩形。例如以元素1为例,它可以扩展到整个数组为矩形。例如以元素5为例,它可以扩展到(左边界为1,右边界为元素2)为矩形。时间复杂度n²
优化:与上题一样,用两个数组分别记录比当前左右位置最小但且最近元素,时间复杂度(n)。空间杂度(n)(前提是要有这样的两个数组)。
但这题要找到的是最小元素还得是离自己最近的元素,似乎又要暴力遍历了啊。。。。。这里可以使用前面介绍的单调栈来解决。
例如:数组 2 1 5 6 2 3为例,先找到比当前位置小且最近且在右边的元素。(用栈模拟,从后往前遍历,若栈为空,则填入数组的大小(这里方便计算宽度),若当前元素比栈顶元素小,则持续将栈顶元素出栈,直到栈顶元素比当前元素小,填入栈顶元素下标)
例如:数组 2 1 5 6 2 3为例
比它当前元素小且最近的数组,这里记录下标,后面方便计算宽度
Ri: 1 6 4 4 6 6
Lf: -1 -1 1 2 1 4
代码:
class Solution {
public:
int largestRectangleArea(vector& heights) {
vector Lf(heights.size()+1,0);
vector Ri(heights.size()+1,0);
stack s1_;
stack s2_;
int maxcount=0;
for(int i=0;i=0;i--)
{
while(!s2_.empty()&&heights[i]<=heights[s2_.top()])
{
s2_.pop();
}
if(s2_.empty())
Ri[i]=heights.size();
else
Ri[i]=s2_.top();//记录比当前元素小且在其右边边且最近的元素下标
s2_.push(i);
}
for(int i=0;i 解法2:
思路:对于一个高度,如果能得到向左和向右的边界,那么就可以计算其面积。例如
当数组元素一直在递增时,那么当前的元素都可以向右扩展,直到遇到比自己小的元素。
用栈模拟实现,当元素递增时,可以将元素入栈,当遇到比栈顶元素小的元素时,说明以栈顶元素为基准的矩形不能再往右扩展了,可以计算其矩形面积了。
class Solution {
public:
int largestRectangleArea(vector& heights)
{
int ans = 0;
vector st;
heights.insert(heights.begin(), 0);
heights.push_back(0);
for (int i = 0; i < heights.size(); i++)
{
while (!st.empty() && heights[st.back()] > heights[i])
{
int cur = st.back();
st.pop_back();
int left = st.back() + 1;
int right = i ;
ans = max(ans, (right - left) * heights[cur]);
}
st.push_back(i);
}
return ans;
}
};