地理空间索引实现：z 曲线、希尔伯特曲线、四叉树, 最邻近几何特征查询、范围查询

我的GIS/CS学习笔记：https://github.com/yunwei37/ZJU-CS-GIS-ClassNotes
<一个浙江大学本科生的计算机、地理信息科学知识库 >
详细代码可在其中查看

空间索引

在谈论空间索引之前，我们必须了解数据索引的概念：索引是为了提高数据集的检索效率。打个比喻，一本书的目录就是这本书的内容的“索引”，我们查看感兴趣的内容前，通过查看书的目录去快速查找对应的内容，而不是一字一句地找我们感兴趣的内容；就像这样，事先构建的索引可以有效地加速查询的速度。

然而，和一般的数据相比，有效地查询地理空间数据是相当大的挑战，因为数据是二维的（有时候甚至更高），不能用如传统的B+树这样标准的索引技术来加速查询位置相关的数据。因此，我们就引入了空间索引技术来解决这个问题。

空间索引的定义：

依据空间实体的位置和形状或空间实体之间的某种空间关系，按一定顺序排列的一种数据结构，其中包含空间实体的概要信息，如对象的标识，最小边界矩形及指向空间实体数据的指针

常见的空间索引技术有网格索引、四叉树索引，空间填充曲线索引，以及最用于地理空间数据库的R树索引以及相关变体等等。

网格索引

网格索引的基本思想是将研究区域用横竖线划分大小相等和不等的网格，每个网格可视为一个桶(bucket)，构建时记录落入每一个网格区域内的空间实体编号。

进行空间查询时，先计算出查询对象所在网格，再在该网格中快速查
询所选空间实体

• 网格索引优点：简单，易于实现，具有良好的可扩展性；

• 网格索引缺点：网格大小影响网格索引检索性能

理想的情况下，网格大小是使网格索引记录不至于过多，同时每个网格内的要素个数的均值与最大值尽可能地少。如要获得较好的网格划分，可以根据用户的多次试验来获得经验最佳值， 也可以通过建立地理要素的大小和空间分布等特征值来定量确定网格大小。

网格索引的实现这里暂时没有涉及。

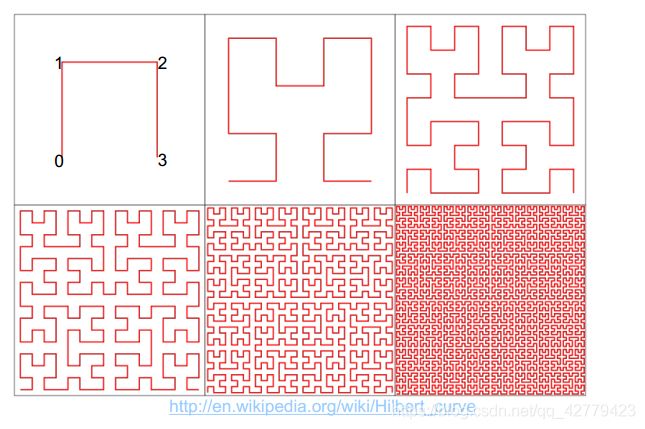
空间填充曲线索引

常用的空间索引曲线有z曲线、希尔伯特曲线，其目的是在空间网格的基础上降低空间维度，以便于在顺序读取的磁盘上存取信息。

空间填充曲线(space-filling curve)是一条连续曲线，自身没有任何交叉；通过访问所有单元格来填充包含均匀网格的四边形。

• z曲线
  

• 希尔伯特曲线
  

Z曲线和Hilbert曲线共同特点：

• 填充曲线值临近的网格，其空间位置通常也相对临近；
• 任何一种空间排列都不能完全保证二维数据空间关系的维护（编号相邻，空间位置可能很远）

不同点：

• Hilbert曲线的数据聚集特性更优，Z曲线的数据聚集特性较差
• Hilbert曲线的映射过程较复杂，Z曲线的映射过程较简单

z曲线实现：

Z-curve曲线的二维坐标与Z值的相互转换：

基于bit-shuffling思想，实现二维坐标(coor)与Z值(value)的相互转换。order为Z-Curve的阶数，order为4时，平面网格大小为(2^4, 2^4)，即16x16。

/*
 * zorder - Calculate the index number (Z-value) of the point (represented by coordinate) in the Z-curve with given order
 */
void zorder(int order, int& value, int coor[2])
{
	// Calculate the z-order by bit shuffling
	value = 0;
	for (int i = 0; i < 2; ++i) {
		for (int j = 0; j < order; ++j) {
			// Task 1.1 zorder，修改以下代码
			int mask = 1<<j;
			// Check whether the value in the position is 1
			if (coor[1-i] & mask)
				// Do bit shuffling
				value |= 1 << (i + j*2);
		}
	}
}

/*
 * izorder - Calculate the coordinate of the point with given Z-value and order
 */
void izorder(int order, int value, int coor[2])
{
	// Initialize the coordinate to zeros
	for (int i = 0; i < 2; ++i)
		coor[i] = 0;
	// Task 1.2 izoder
	// Write your code here
	for (int i = 0; i < 2; ++i) {
		for (int j = 0; j < order; ++j) {
			// Task 1.1 zorder，修改以下代码
			int mask = 1 << j*2+i;
			// Check whether the value in the position is 1
			if (value & mask)
				// Do bit shuffling
				coor[1-i] |= 1 << j;
		}
	}
}

希尔伯特曲线实现

Hilbert Curve的二维坐标与H值的相互转换：

基于linear-quadtrees递归填充思想，实现二维坐标(coor)到H值(value)的相互转换。order为Hilbert Curve的阶数，order为4时，平面网格大小为(2^4, 2^4)，即16x16。

/*
 * horder - Calculate the index number (H-value) of the point (represented by coordinate) in Hilbert curve with given order
 */
void horder(int order, int& value, int coor[2])
{
	// order = 1
	int num = int(pow(2, 1));
	int * hcurve = new int[num * num];
    hcurve[0] = 1;
    hcurve[1] = 2;
    hcurve[2] = 0;
    hcurve[3] = 3;

    for(int i = 2; i <= order; ++i) {
		int add = (int)pow(2, 2 * i - 2);		// the number of values in order - 1
		int blockLen = (int)pow(2, i - 1);
		int * temp = hcurve;

        num = int(pow(2, i));
		hcurve = new int[num * num];

		for (int j = 0; j < blockLen; ++j) {
			for (int k = 0; k < blockLen; ++k) {
				// Task 2.1 horder，修改以下四行代码
				hcurve[j * num + k] = temp[j * blockLen + k] + add;
				hcurve[j * num + k + blockLen] = temp[j * blockLen + k] + add*2;
				hcurve[(j + blockLen) * num + k] = temp[(blockLen - k-1) * blockLen + (blockLen - j-1)] + 0;
				hcurve[(j + blockLen) * num + k + blockLen] = temp[k * blockLen + j] + add * 3;
			}
		}

		delete temp;
    }

	// Task 2.1 horder，修改以下一行代码
	value = hcurve[num*(num - coor[1] - 1)+coor[0]];
	delete[] hcurve;
}

/*
 * ihorder - Calculate the coordinate of the point with given H-value and order
 */
void ihorder(int order, int value, int coor[2])
{
	// order = 1
	int num = int(pow(2, 1));
	int * hcurve = new int[num * num];
	hcurve[0] = 1;
	hcurve[1] = 2;
	hcurve[2] = 0;
	hcurve[3] = 3;
	
	for (int i = 2; i <= order; ++i) {
		int add = (int)pow(2, 2 * i - 2);		// the number of values in order - 1
		int blockLen = (int)pow(2, i - 1);
		int* temp = hcurve;

		num = int(pow(2, i));
		hcurve = new int[num * num];

		for (int j = 0; j < blockLen; ++j) {
			for (int k = 0; k < blockLen; ++k) {
				// Task 2.1 horder，修改以下四行代码
				hcurve[j * num + k] = temp[j * blockLen + k] + add;
				hcurve[j * num + k + blockLen] = temp[j * blockLen + k] + add * 2;
				hcurve[(j + blockLen) * num + k] = temp[(blockLen - k - 1) * blockLen + (blockLen - j - 1)] + 0;
				hcurve[(j + blockLen) * num + k + blockLen] = temp[k * blockLen + j] + add * 3;
			}
		}

		delete temp;
	}
	for (int i = 0; i < 2; ++i)
		coor[i] = 0;
	int i = 0;
	for (; i < num * num; ++i) {
		if (value == hcurve[i])
			break;
	}
	coor[0] = i % num;
	coor[1] = num - 1 - i / num;
	delete[] hcurve;
}

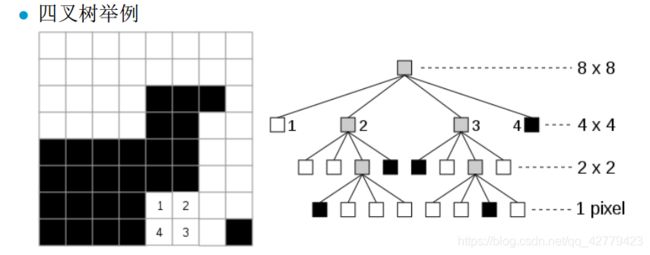
四叉树索引

四叉树索引是在网格索引的思想基础上，为了实现要素真正被网格分割，同时保证桶内要素不超过一个量而提出的一种空间索引方法。

构造方法：

1. 首先将整个数据空间分割成为四个相等的矩阵，分别对应西北(NW)，东北(NE)，西南(SW)，东南(SE)四个象限；
2. 若每个象限内包含的要素不超过给定的桶量则停止，否则对超过桶量的矩形再按照同样的方法进行划分，直到桶量满足要求或者不再减少为止，最终形成一颗有层次的四叉树。
   
   四叉树优缺点：

• 与网格索引相比，四叉树在一定程度上实现了地理要素真正被网格分割，保证了桶内要素不超过某个量，提高了检索效率；
• 对于海量数据，四叉树的深度会很深，影响查询效率
• 可扩展性不如网格索引：当扩大区域时，需要重新划分空间区域，重建四叉树，当增加或删除一个对象，可能导致深度加一或减一，叶节点也有可能重新定位。

四叉树索引构建：

四叉树创建输入一组几何特征，将节点分裂为四个子节点，每个特征加到包围盒重叠的子节点中（即一个特征可能在多个节点中），删除当前节点的几何特征记录（即所有特征只存储在叶节点中），如果子节点的几何特征个数大于capacity，递归分裂子节点。

/*
 * QuadNode
 */
void QuadNode::split(size_t capacity)
{
	for (int i = 0; i < 4; ++i) {
		delete []nodes[i];
		nodes[i] = NULL;
	}
	
	if (features.size() > capacity) {
		double midx = (bbox.getMinX() + bbox.getMaxX()) / 2.0;
		double midy = (bbox.getMinY() + bbox.getMaxY()) / 2.0;
		Envelope e0(bbox.getMinX(), midx, midy, bbox.getMaxY());
		nodes[0] = new QuadNode(e0);
		Envelope e1(midx, bbox.getMaxX(), midy, bbox.getMaxY());
		nodes[1] = new QuadNode(e1);
		Envelope e2(midx, bbox.getMaxX(), bbox.getMinY(), midy);
		nodes[2] = new QuadNode(e2);
		Envelope e3(bbox.getMinX(), midx, bbox.getMinY(), midy);
		nodes[3] = new QuadNode(e3);

		for (Feature f : features) {
			for (int i = 0; i < 4; ++i) {
				if (nodes[i]->getEnvelope().intersect(f.getEnvelope())) {
					nodes[i]->add(f);
				}
			}
		}

		for (int i = 0; i < 4; ++i) {
			nodes[i]->split(capacity);
		}
		features.clear();
	}
}

/*
 * QuadTree
 */
bool QuadTree::constructQuadTree(vector<Feature>& features)
{
	if (features.empty())
		return false;

	// Task 5.1 construction
	// Write your code here

	Envelope e(DBL_MAX, -DBL_MAX, DBL_MAX, -DBL_MAX);
	for (Feature f : features) {
		e = e.unionEnvelope(f.getEnvelope());
	}
	root = new QuadNode(e);

	root->add(features);

	root->split(capacity);

	bbox = e; // 注意此行代码需要更新为features的包围盒，或根节点的包围盒
	//bbox = Envelope(-74.1, -73.8, 40.6, 40.8);
	return true;
}

效果：

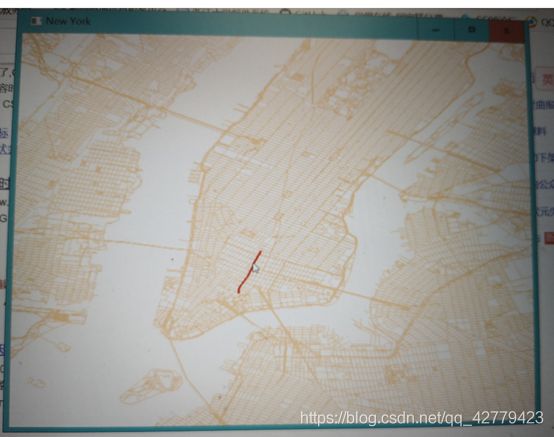
四叉树上的最邻近几何特征查询、范围查询：

最邻近几何特征查询：

最邻近几何特征查询(K-NN)输入查询点(x, y)，返回与该点最邻近的几何特征，存储在feature。首先，通过pointInLeafNode查询点(x, y)所在的叶节点，计算查询点(x, y)与该叶节点内的几何特征包围盒的最大距离的最小值minDist，即通过包围盒而非原始几何加速最小距离计算；然后，构造查询区域 (x – minDist, x + minDist, y – minDist, y + minDist)，查询几何特征的包围盒与该区域相交的几何特征（filter），再查询与查询点(x, y)距离最近的几何特征（refine）。

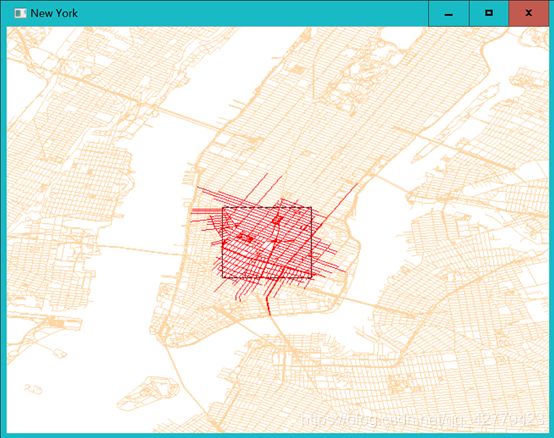
范围查询：

区域查询输入区域rect，查询与区域rect相交的几何特征，存储在features。区域rect如果与当前节点的包围盒bbox相交，递归遍历四叉树，查询哪些几何特征的包围盒和查询区域相交（filter）；再获得可能和查询区域相交的候选几何特征后，精确判断几何特征是否与查询区域相交（refine）。

效果：

具体代码可在我的github项目中查看：

https://github.com/yunwei37/myClassNotes