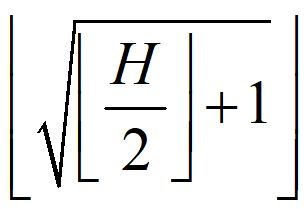蓝桥杯2022初赛
一、[蓝桥杯2022初赛] 九进制转十进制
九进制正整数(2022) 转换成十进制等于多少?
这是一道结果填空的题,你只需要算出结果后提交即可。
本题的结果为一个整数,在提交答案时只输出这个整数,输出多余的内容将无法得分。
本体为基本的进制转换问题个位乘以 (9的0次方) 加上 十位乘以 (9的一次方) 加上 百位乘以 (9的二次方)。也即2*1+2*9+0*9*9+2*9*9*9;
代码如下:
#include
using namespace std;
int main()
{
cout << 2 + 2 * 9 + 2 * 9 * 9 * 9 << endl;
} 二、 [蓝桥杯2022初赛] 顺子日期
小明特别喜欢顺子。顺子指的就是连续的三个数字:123、456 等。
顺子日期指的就是在日期的 yyyymmdd 表示法中,存在任意连续的三位数是一个顺子的日期。
例如20220123 就是一个顺子日期,因为它出现了一个顺子:123;
本题顺子的定义:i j k 是一个顺子,满足 i+1=j、j+1=k、i≥0。
而20221023 则不是一个顺子日期,它一个顺子也没有。
小明想知道在整个2022年份中,一共有多少个顺子日期。
这是一道结果填空的题,你只需要算出结果后提交即可。
本题的结果为一个整数,在提交答案时只输出这个整数,输出多余的内容将无法得分。
根据日期进行遍历即可。
代码如下:
#include
using namespace std;
int month[13] = { 0,31,28,31,30,31,30,31,31,30,31,30,31 };
int main()
{
int get[4];
int count = 0;
for (int i = 20220101; i <= 20221231; i++)
{
get[0] = i % 10;
get[1] = (i/10) % 10;
get[2] = (i / 100) % 10;
get[3] = (i / 1000) % 10;
if (get[3] * 10 + get[2] <= 12 && get[3] * 10 + get[2] >= 1)
{
if (get[1] * 10 + get[0] >= 1 && get[1] * 10 + get[0] <= month[get[3] * 10 + get[2]])
{
if (get[3] + 1 == get[2] && get[2] + 1 == get[1] || get[2] + 1 == get[1] && get[1] + 1 == get[0])
{
count++;
}
}
}
}
cout << count << endl;
} 三、 [蓝桥杯2022初赛] 刷题统计
小明决定从下周一开始努力刷题准备蓝桥杯竞赛。
他计划周一至周五每天做 a 道题目,周六和周日每天做 b 道题目。
请你帮小明计算,按照计划他将在第几天实现做题数大于等于 n 题?
通过简要模拟即可得到:
#include
using namespace std;
int main()
{
long long a, b, n;
long long sum = 0; int i;
scanf("%lld%lld%lld", &a, &b, &n);
long long week = n / (a * 5 + b * 2);
long long orther=n-week* (a * 5 + b * 2);
sum = week * 7;
for (i = 1; i <= 7; i++)
{
if(orther >0)
{
if (i < 6)orther -= a;
else orther -= b;
sum++;
}
}
cout << sum< 四、[蓝桥杯2022初赛] 修剪灌木
爱丽丝要完成一项修剪灌木的工作。
有 N 棵灌木整齐的从左到右排成一排。
爱丽丝在每天傍晚会修剪一棵灌木,让灌木的高度变为 0 厘米。
爱丽丝修剪灌木的顺序是从最左侧的灌木开始,每天向右修剪一棵灌木。
当修剪了最右侧的灌木后,她会调转方向,下一天开始向左修剪灌木。
直到修剪了最左的灌木后再次调转方向。然后如此循环往复。
灌木每天从早上到傍晚会长高 1 厘米,而其余时间不会长高。
在第一天的早晨,所有灌木的高度都是 0 厘米。爱丽丝想知道每棵灌木最高长到多高。
每棵灌木所拥有的生长时间分别为i,2*(n-i),2*(i-1)三段。
#include
#include
using namespace std;
int main()
{
int n, i;
cin >> n;
for (int i = 1; i <= n; i++)
{
cout << max({ i,2 * (n - i),2 * (i - 1) })< 五、[蓝桥杯2022初赛] X进制减法
进制规定了数字在数位上逢几进一。
X 进制是一种很神奇的进制,因为其每一数位的进制并不固定!
例如说某种X 进制数,最低数位为二进制,第二数位为十进制,第三数位为八进制:
则 X 进制数321 转换为十进制数为65。65=3*(2*10)+2*(2)+1*(1)。
现在有两个 X 进制表示的整数 A 和 B,但是其具体每一数位的进制还不确定。
只知道 A 和 B 是同一进制规则,且每一数位最高为 N 进制,最低为二进制。
请你算出 A − B 的结果最小可能是多少。
请注意,你需要保证 A 和 B 在 X 进制下都是合法的,即每一数位上的数字要小于其进制。
第一行一个正整数 N,含义如题面所述。
第二行一个正整数 Ma,表示 X 进制数 A 的位数。
第三行 Ma 个用空格分开的整数,表示 X 进制数 A 按从高位到低位顺序各个数位上的数字在十进制下的表示。
第四行一个正整数 Mb,表示 X 进制数 B 的位数。
第五行 Mb 个用空格分开的整数,表示 X 进制数 B 按从高位到低位顺序各个数位上的数字在十进制下的表示。
请注意,输入中的所有数字都是十进制的。
30%的测试数据:2≤N≤10,1≤Ma,Mb≤8。
100%的测试数据:2≤N≤1000,1≤Ma,Mb≤100000,B≤A。
A:An-1,An-2,...,A1,A0;
B:Bn-1,Bn-2,...,B1,b0;
A-B=((An-1)-(Bn-1))*(Pn-2*Pn-3*...*P1*p0)+((An-2)-(Bn-2))*(Pn-3*Pn-4*...*P1*P0)+...+(A1-B1)*P0+A0-B0;
#include
#include
#include
using namespace std;
const int maxn = 1000000007;
int A[1000005], B[1000005];
int main()
{
int N;
scanf("%d", &N);
int len1,len2;
scanf("%d", &len1);
memset(A, 0, sizeof(A));
memset(B, 0, sizeof(B));
for (int i = len1 - 1; i >= 0; i--)
{
scanf("%d", &A[i]);
}
scanf("%d", &len2);
for (int i = len2 - 1; i >= 0; i--)
{
scanf("%d", &B[i]);
}
long long result=0;
for (int i = len1 - 1; i >= 0; i--)
{
result = (result * (max({A[i],B[i],1}) + 1) + A[i] - B[i])%maxn;
}
cout << result << endl;
} 六、[蓝桥杯2022初赛] 统计子矩阵
给定一个 N × M 的矩阵A,请你统计有多少个子矩阵(最小 1 × 1,最大 N × M) 满足:
子矩阵中所有数的和不超过给定的整数K?
第一行包含三个整数N, M 和K.
之后 N 行每行包含 M 个整数,代表矩阵A.
30%的测试数据:1≤N,M≤20;
70%的测试数据:1≤N,M≤100;
100%的测试数据:1≤N,M≤500;0≤Aij≤1000;1≤K≤250000000。
用前缀和加上双指针扫描:
#include
#include
using namespace std;
int s[600][600];
int main()
{
int n, m;
long long k, ans = 0;
cin >> n >> m >> k;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> s[i][j];
s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
}
}
for (int l = 1; l <= m; l++)
{
for (int r = l; r <= m; r++)
{
for (int i = 1, j = 1; i <= n; i++)
{
while (j <= i && s[i][r] - s[j - 1][r] - s[i][l - 1] + s[j - 1][l - 1] > k)j++;
if (j <= i)ans += (i - j + 1);
}
}
}
cout << ans << endl;
return 0;
} 七、[蓝桥杯2022初赛] 积木画
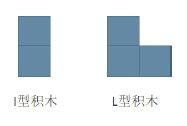
小明最近迷上了积木画,有这么两种类型的积木,分别为 I 型(大小为 2 个单位面积)和 L 型(大小为 3 个单位面积):
同时,小明有一块面积大小为 2 × N 的画布,画布由 2 × N 个 1 × 1 区域构成。
小明需要用以上两种积木将画布拼满,他想知道总共有多少种不同的方式?
积木可以任意旋转,且画布的方向固定。
#include
#include
using namespace std;
const int N = 1e7 + 4, C = 1e9 + 7;
#define max 10000000
long long dp[max],sum[max];
int main()
{
int n;
cin >> n;
dp[0] = sum[0] = 1;
dp[1] = 1;
dp[2] = 2;
for(int i=3; i<=n ; i++)
{
dp[i] = (dp[i - 1] + dp[i - 2] + 2 * sum[i - 3]) % C;
sum[i - 2] = (sum[i - 3] + dp[i - 2]) % C;
}
cout << dp[n];
return 0;
} 八、[蓝桥杯2022初赛] 扫雷
小明最近迷上了一款名为《扫雷》的游戏。
其中有一个关卡的任务如下,在一个二维平面上放置着 n 个炸雷
第 i 个炸雷(xi, yi, ri) 表示在坐标(xi, yi) 处存在一个炸雷,它的爆炸范围是以半径为 ri 的一个圆。
为了顺利通过这片土地,需要玩家进行排雷。
玩家可以发射 m 个排雷火箭,小明已经规划好了每个排雷火箭的发射方向。
第 j 个排雷火箭(xj, yj, rj) 表示这个排雷火箭将会在(xj, yj) 处爆炸,它的爆炸范围是以半径为 rj 的一个圆,可以存在多个炸雷和排雷火箭。当炸雷位于爆炸范围的边界上时也会被引爆。
在其爆炸范围内的炸雷会被引爆。同时,当炸雷被引爆时,在其爆炸范围内的炸雷也会被引爆。
现在小明想知道他这次共引爆了几颗炸雷?
你可以把炸雷和排雷火箭都视为平面上的一个点。
一个点处输入的第一行包含两个整数n、m.
接下来的 n 行,每行三个整数xi, yi, ri,表示一个炸雷的信息。
再接下来的 m 行,每行三个整数xj, yj, rj,表示一个排雷火箭的信息。
40% 的评测用例:0 ≤ x, y ≤ 10^9; 0 ≤ n,m ≤ 10^3; 1 ≤ r ≤ 10:
100% 的评测用例:0 ≤ x, y ≤ 10^9; 0 ≤ n,m ≤ 5 × 10^4; 1 ≤ r ≤ 10:
#include
#include
#include
using namespace std;
long long n, m, ans;
double dis(double x1, double y1, double x2, double y2) {
return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}
struct zhalei
{
long long x, y, r;
bool flag = 0;
}a[50005];
struct pailei
{
long long x, y, r;
}b[50005];
bool cmp(zhalei a, zhalei b)
{
return a.x < b.x;
}
void dfs(int x, int y, int r) {
int Lmid, Rmid, L = 1, R = n;
while (L <= R) {
Lmid = (L + R) / 2;
if (a[Lmid].x < x - r)L = Lmid + 1;
else R = Lmid - 1;
}
Lmid = L;
L = 1, R = n;
while (L <= R) {
Rmid = (L + R) / 2;
if (a[Rmid].x <= x + r)L = Rmid + 1;
else R = Rmid - 1;
}
for (long long i = Lmid; i <= Rmid; i++) {
if (!a[i].flag && dis(x, y, a[i].x, a[i].y) <= r) {
a[i].flag = 1, ans++;
dfs(a[i].x, a[i].y, a[i].r);
}
}
}
int main() {
long long i;
scanf("%lld%lld", &n, &m);
for (i = 1; i <= n; i++)scanf("%lld%lld%lld", &a[i].x, &a[i].y, &a[i].r);
for (i = 1; i <= m; i++)scanf("%lld%lld%lld", &b[i].x, &b[i].y, &b[i].r);
sort(a + 1, a + n + 1, cmp);
for (i = 1; i <= m && ans < n; i++)
dfs(b[i].x, b[i].y, b[i].r);
printf("%lld", ans);
return 0;
} 九、[蓝桥杯2022话说初赛] 李白打酒加强版
话说大诗人李白,一生好饮。幸好他从不开车。
一天,他提着酒壶,从家里出来,酒壶中有酒 2 斗。他边走边唱:
无事街上走,提壶去打酒。
逢店加一倍,遇花喝一斗。
这一路上,他一共遇到店 N 次,遇到花 M 次。
已知最后一次遇到的是花,他正好把酒喝光了。
请你计算李白这一路遇到店和花的顺序,有多少种不同的可能?
注意:壶里没酒( 0 斗) 时遇店是合法的,加倍后还是没酒;但是没酒时遇花是不合法的。
输入包含多组测试数据。
第一行为T,表示存在T组测试数据,T不超过30。
对于每组测试数据,输入两个整数N 和M.
1 ≤ N, M ≤ 100。
#include
using namespace std;
int n, m;
int f[205][105][105];
int main() {
cin >> n >> m;
f[0][0][2] = 1;
for (int i = 0; i < n + m; i ++)
for (int j = 0; j < m; j ++)
for (int k = 0; k <= m; k ++)
if (f[i][j][k]) {
if (k > 0) f[i + 1][j + 1][k - 1] = (f[i + 1][j + 1][k - 1] + f[i][j][k]) % 1000000007;
if (k <= 50) f[i + 1][j][k * 2] = (f[i + 1][j][k * 2] + f[i][j][k]) % 1000000007;
}
cout << f[n + m][m][0];
return 0;
} 十、[蓝桥杯2022初赛] 砍竹子
这天,小明在砍竹子,他面前有 n 棵竹子排成一排,一开始第 i 棵竹子的高度为 hi.
他觉得一棵一棵砍太慢了,决定使用魔法来砍竹子。
魔法可以对连续的一段相同高度的竹子使用,假设这一段竹子的高度为H,
那么使用一次魔法可以把这一段竹子的高度都变为:
其中 ⌊x⌋ 表示对 x 向下取整。
小明想知道他最少使用多少次魔法可以让所有的竹子的高度都变为1。
第一行为一个正整数 n,表示竹子的棵数。
第二行共 n 个空格分开的正整数 hi,表示每棵竹子的高度。
20%的测试数据:n ≤ 1000; hi ≤ 10^6。
100%的测试数据:n ≤ 2 × 10^5; hi ≤ 10^18。
#include
using namespace std;
#define N 200005
#define int long long
#define For(i, j, n) for(int i = j ; i <= n ; ++i)
int n, cnt, fa[N];
struct node{
int h, p;
friend bool operator < (node x, node y){
if(x.h == y.h) return x.p < y.p;
return x.h < y.h;
}
}t, a[N];
inline int find(int x){ return fa[x] ^ x ? fa[x] = find(fa[x]) : x; }
signed main(){
scanf("%lld", &n);
priority_queueq;
For(i, 1, n) scanf("%lld", &a[i].h), a[i].p = fa[i] = i;
For(i, 2, n) if(a[i].h == a[i - 1].h) fa[find(i)] = find(i - 1);
For(i, 1, n) if(find(i) == i && a[i].h > 1) q.push(a[i]);
while(!q.empty()){
t = q.top();
q.pop();
if(t.h == a[find(t.p - 1)].h) fa[find(t.p)] = find(t.p - 1);
if(find(t.p) ^ t.p) continue;
a[t.p].h = t.h = sqrt((int)(t.h / 2) + 1);
if(t.h > 1) q.push(t);
++cnt;
}
printf("%lld", cnt);
return 0;
}