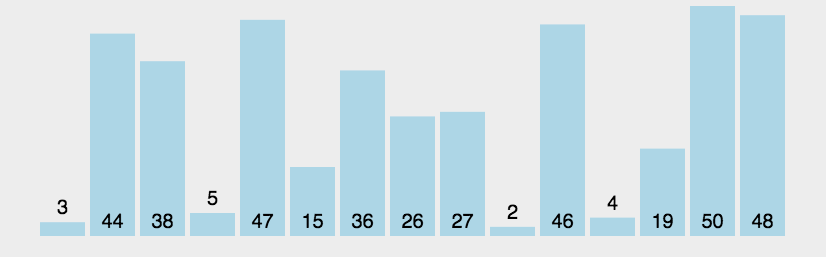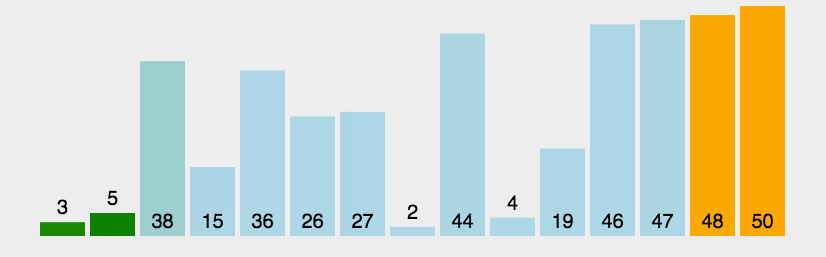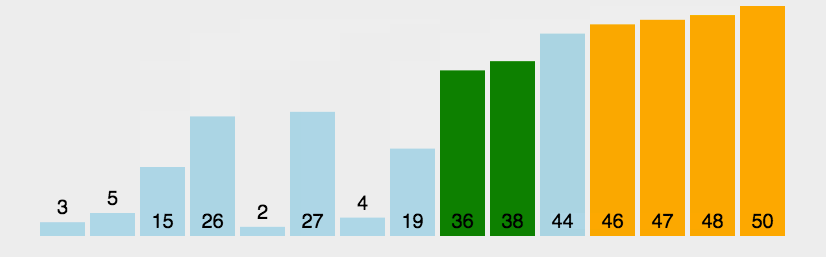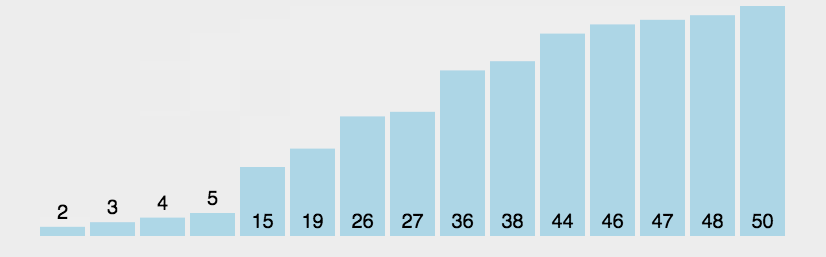【算法】排序算法(插入排序、希尔排序、选择排序、冒泡排序、快速排序、归并排序、基数排序、堆排序)

一.常见排序类型

• 插入排序：插入排序、希尔排序
• 选择排序：选择排序、堆排序
• 交换排序：冒泡排序、快速排序
• 归并排序
• 基数排序(又叫桶排序)

二.排序详解

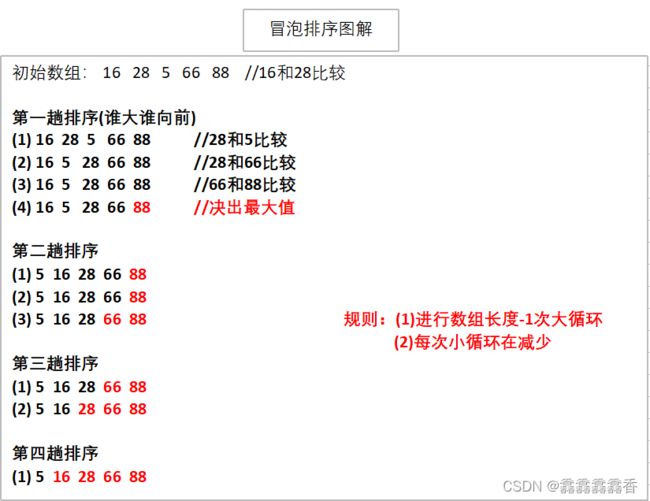
1.冒泡排序

(1)思路图解

从头开始比较相邻元素的值(就是从下标较小的元素开始)，使值较大的元素逐渐从前移向后部，就像水里的气泡一样，越来越大，向上冒。最终得到从小到大的一个序列。

(2)算法实现(java)

/**
 * 冒泡排序
 * author：xinxin
 * 时间复杂度是(n*n)
 */
public class GuLouSort {
    public static void main(String[] args) {
        int[] arr = {16,28,5,66,88}; //初始化数组
        int temp = 0; //临时变量
        for (int i = 0; i < arr.length-1; i++){ //代表大循环  第几趟
            for (int j = 0; j < arr.length-1-i; j++){ //代表小循环
                if (arr[j] > arr[j+1]){ //如果前面的值大于前面的值，那就交换位置
                    temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
            }
            System.out.println("第"+(i+1)+"趟，排序后的结果");
            System.out.println(Arrays.toString(arr));
        }
    }
}

运行结果

2.选择排序

(1)思路图解

先从arr[0] ~ arr[n-1]找到一个最小值，和arr[0]交换，在从arr[1] ~ arr[n-1]中找到最小值，和arr[1]交换，以此类推，最终得到一个从小到大排列的序列。

(2)算法实现(java)

/**
 * 选择排序
 * author：xinxin
 * 时间复杂度是(n*n)
 */
public class SelectSort {
    public static void main(String[] args) {
        int[] arr = {16,6,88,2}; //初始化数组
        for (int i = 0; i < arr.length-1; i++) { //代表第几轮循环
            int minIndex = i; //假定最小下标
            int minArr = arr[i]; //假定最小的值
            for (int j = i+1; j < arr.length; j++) { //代表每轮循环中去查找最小的值
                if (minArr > arr[j]){ //如果假定的最小值比他后面的值要大,记录下标和值(这个地方控制是从大到小排序还是从小到大排序)
                    minIndex = j;    //记录下标
                    minArr = arr[j]; //记录值
                }
            }
            //交换值
            if (minIndex != i){
                arr[minIndex] = arr[i];
                arr[i] = minArr;
            }
            System.out.println("第"+(i+1)+"轮结果为");
            System.out.println(Arrays.toString(arr));
        }
    }
}

运行结果

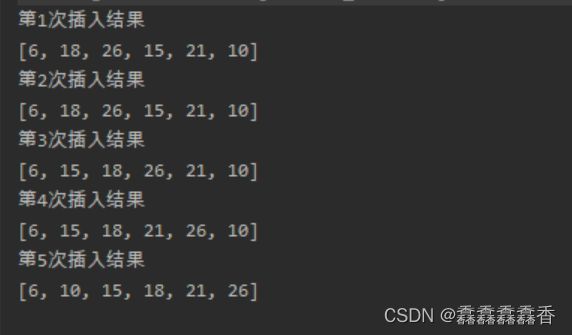
3.插入排序

(1)思路图解

n个元素，分成一个有序序列和无序序列，开始有序序列只有一个元素，无序序列包含n-1个元素，排序时每次从无序序列取出第一个元素，和有序序列的元素的排序码进行比较，然后放到合适的位置，最后形成新的有序序列。

(2)算法实现(java)

/**
 * 插入排序
 * author：xinxin
 */
public class InsertSort {
    public static void main(String[] args) {
        int[] arr = {18, 6, 26, 15,  21,10};//初始化数组
        for (int i = 1; i < arr.length; i++) {
            int currValue = arr[i]; //要插入的元素，从arr[1]开始，因为arr[0]是有序序列第一个元素
            int beforeIndex = i-1; //要插入元素前面的元素的下标
            while(beforeIndex >= 0 && currValue < arr[beforeIndex]){ //判断要插入元素的位置，并且没有找到插入位置(从这里可以改变从大到小排序还是从小到大)
                arr[beforeIndex + 1] = arr[beforeIndex]; //arr[beforeIndex]后移
                beforeIndex--;
            }

            //当退出while循环，找到插入位置
            arr[beforeIndex + 1] = currValue;
            System.out.println("第"+i+"次插入结果");
            System.out.println(Arrays.toString(arr));
        }

    }
}

运行结果

4.希尔排序

(1)思路图解

希尔排序也是一种插入排序，但是更加高效，也称为速效增量排序。
按照一定的增量(步长)进行分组，然后对每组进行插入排序，随着增量减少，每组的元素就越多，当增量减至1时，元素被分为一组，算法结束。

(2)算法实现(交换法)

/**
 * 希尔排序(交换法)
 * author：xinxin
 */
public class ShellSort {
    public static void main(String[] args) {
        int[] arr = {8, 9, 1, 7, 2, 3, 5, 4, 6, 0};//初始数组
        int temp = 0;
        int count = 0;
        //增量
        for (int gap = arr.length/2; gap > 0; gap=gap/2){
            //遍历组中所有元素，gap为步长
            for (int i = gap; i < arr.length; i++){
                for (int j = i - gap; j >= 0; j = j-gap){
                    //如果当前元素大于加上步长的元素，那就交换位置
                    if (arr[j] > arr[j+gap]){
                        temp = arr[j];
                        arr[j] = arr[j+gap];
                        arr[j+gap] = temp;
                    }
                }
            }
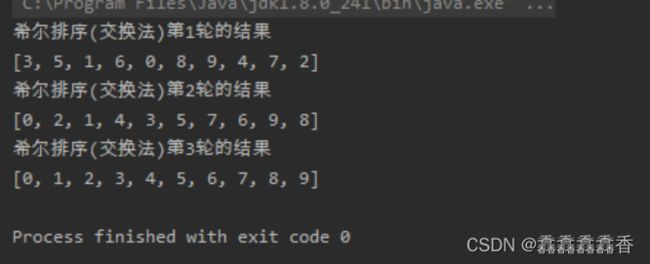
            System.out.println("希尔排序(交换法)第"+(++count)+"轮的结果");
            System.out.println(Arrays.toString(arr));
        }
    }
}

运行结果(交换法)

(3)算法实现(移动法)

/**
 * 希尔排序(移动法)
 * author：xinxin
 */
public class ShellSort2 {
    public static void main(String[] args) {
        int[] arr = {8, 9, 1, 7, 2, 3, 5, 4, 6, 0};//初始数组
        int count = 0;
        for (int gap = arr.length/2; gap > 0; gap = gap/2){
            //从第gap元素开始进行插入排序
            for (int i = gap; i<arr.length; i++){
                int j = i;
                int temp = arr[j];
                if (arr[i] < arr[j - gap]){
                    while(j - gap >= 0 && temp < arr[j - gap]){
                        //移动
                        arr[j] = arr[j - gap];
                        j = j - gap;
                    }
                    arr[j] = temp;
                }
            }
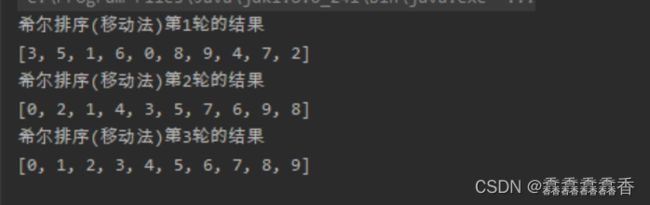
            System.out.println("希尔排序(移动法)第"+(++count)+"轮的结果");
            System.out.println(Arrays.toString(arr));
        }
    }
}

运行结果(移动法)

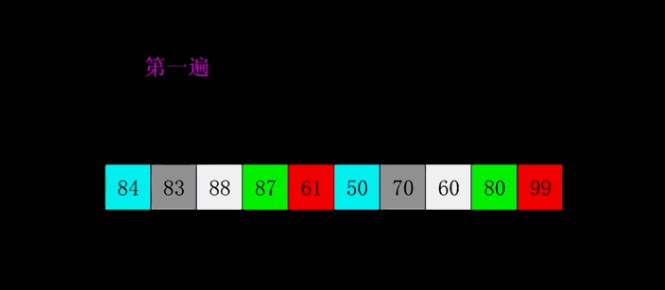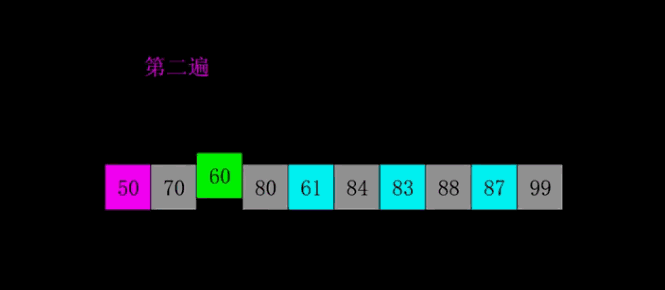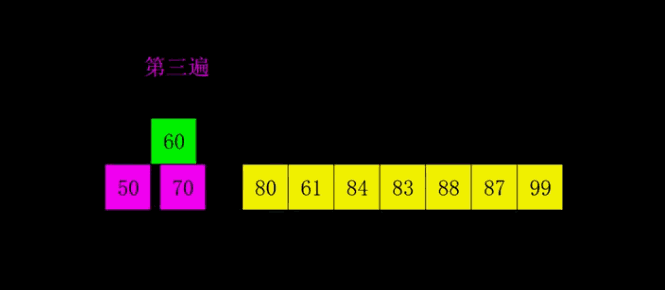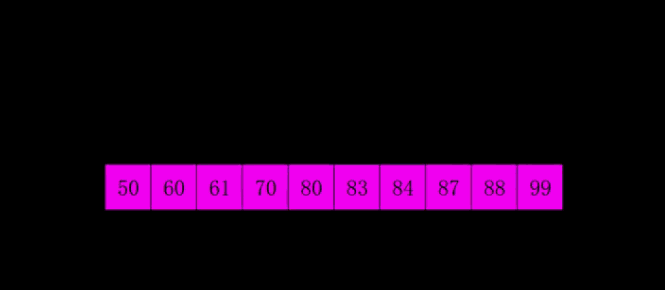
5.快速排序

(1)思路图解

快速排序是对冒泡排序的一种改进。
基本思想是：把需要排序的元素分成两部分，一部分比另一部分都要小，然后进行快速排序，然后递归，最终得到有序序列。

这个图是以第一个元素为中间值分割。（黄色的就相当于中间值，然后把比大小分成两组）

(2)算法实现(java)

/**
 * 快速排序
 * author：xinxin
 */
public class QuikeSort {
    public static void main(String[] args) {
        int[] arr = {1, 66, 2, 28, 0, 18};
        quickeSotr(arr,0,arr.length-1);
        System.out.println("快速排序结果为"+ Arrays.toString(arr));
    }

    public static void quickeSotr(int arr[],int left,int right){
        int l = left;//左下标
        int r = right;//右下标
        int center = arr[(l + r)/2];//中间值
        int temp = 0;//临时变量

        //找到比center值小的放左边，比center值大的放右边
        while(l < r){
        
            //找到比center小的值，才退出
            while (arr[l] < center){
                l = l + 1;
            }
            //找到比center大的值，才退出
            while (arr[r] > center){
                r = r - 1;
            }

            //证明左边都是小于center的数，右边都是大于center的数
            if (l >= r){
                break;
            }
            //交换变量
            temp = arr[l];
            arr[l] = arr[r];
            arr[r] = temp;

            //前移
            if (arr[l] == center){
                r = r - 1;
            }

            //后移
            if (arr[r] == center){
                l = l + 1;
            }
        }

        //如果相等必须进行下面操作，不然会栈溢出
        if (l == r){
            l = l + 1;
            r = r - 1;
        }

        //向左递归
        if (left < r){
            quickeSotr(arr,left,r);
        }

        //向右递归
        if (right > l){
            quickeSotr(arr,l,right);
        }
    }
}

运行结果

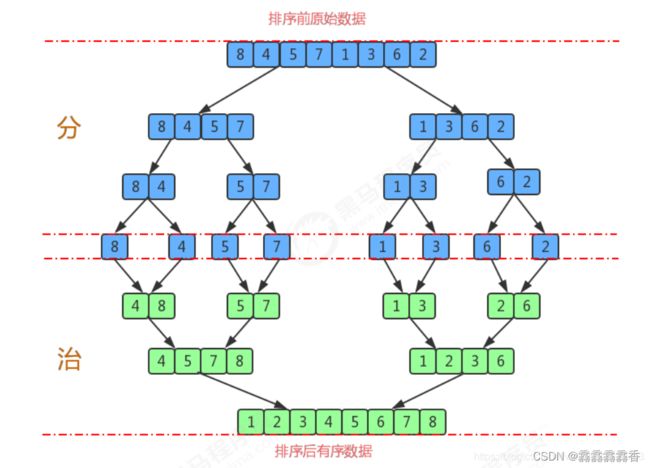
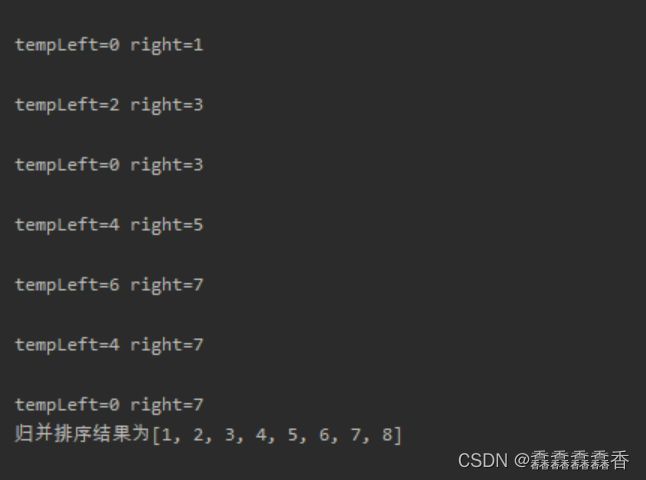
6.归并排序

(1)思路图解

利用归并的思想实现排序，采用分治策略：将问题分成小的问题然后递归求解，而治的阶段将分的阶段得到的结果放一起组合，即分而治之。

下面治的阶段相当于 [4,5,7,8]和[1,2,3,6]各有指针去移动比较两个数组元素大小(和快速排序移动指针一样)，然后放入新的数组。

(2)算法实现(java)

public class MergeSort {
    public static void main(String[] args) {
        int[] arr = {8, 4, 5, 7, 1, 3, 6, 2};
        int[] temp = new int[arr.length];
        mergeSort(arr,0,arr.length-1,temp);
        System.out.println("归并排序结果为"+ Arrays.toString(arr));
    }

    /**
     * 分 + 合
     * @param arr
     * @param left
     * @param right
     * @param temp
     */
    public static void mergeSort(int[] arr, int left, int right, int[] temp) {
        if (left < right){
            int center = (left + right)/2;//中间索引
            mergeSort(arr,left,center,temp);//左递归
            mergeSort(arr,center + 1,right,temp);//右递归
            merge(arr,left,center,right,temp);//合并(治)
        }
    }
        /**
         * 合并的方法
         * 
         * @param arr 原数组
         * @param left 左下标
         * @param center 中间值
         * @param right 右下标
         * @param temp 中转数组
         */
    public static void merge(int[] arr, int left, int center, int right, int[] temp){
        int i = left;//左边序列初始索引
        int j = center + 1;//右边序列初始索引
        int t = 0;//temp数组初始下标

        //把左右两边的有序序列按规则填充到temp中
        while(i <= center && j <= right){
            //当左边序列元素小于右边序列元素，把左边序列元素放进temp数组中
            if (arr[i] < arr[j]){
                temp[t] = arr[i];
                i = i + 1;
                t = t + 1;
            }else{//反之，将右边序列元素放进temp数组中
                temp[t] = arr[j];
                j = j + 1;
                t = t + 1;
            }
        }
        //左边序列剩余元素放进temp数组
        while(i <= center){
            temp[t] = arr[i];
            i = i + 1;
            t = t + 1;
        }

        //右边序列剩余元素放进temp数组
        while(j <= right){
            temp[t] = arr[j];
            j = j + 1;
            t = t + 1;
        }
        
        //将temp拷贝到arr，有可能不是全部拷贝
        t = 0;
        int tempLeft = left;
        System.out.println(" ");
        System.out.println("tempLeft="+tempLeft+" right="+right);
        while (tempLeft < right){
            arr[tempLeft] = temp[t];
            tempLeft = tempLeft + 1;
            t = t + 1;
        }
    }
}

运行结果

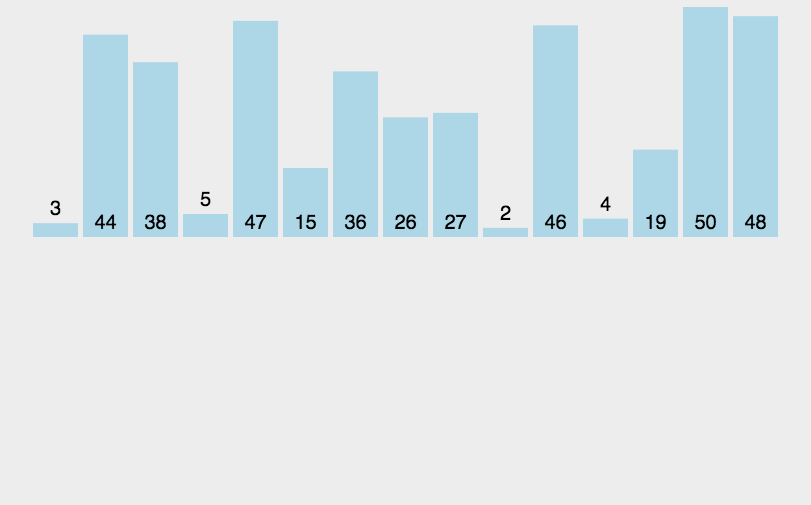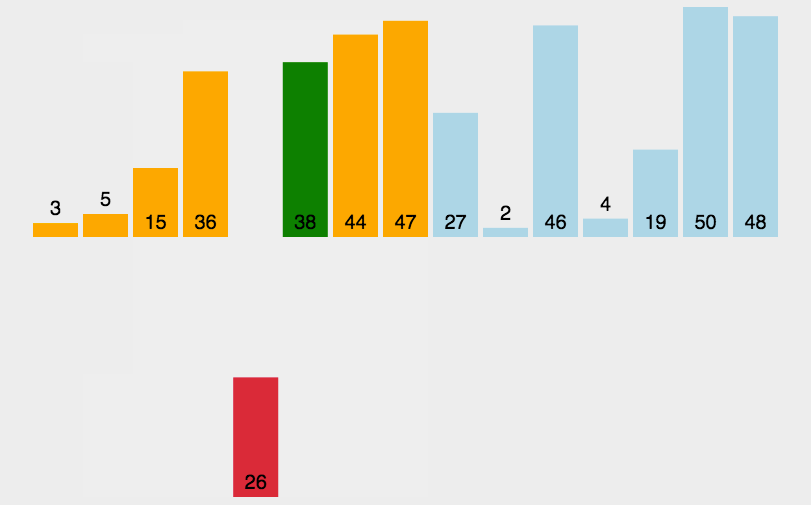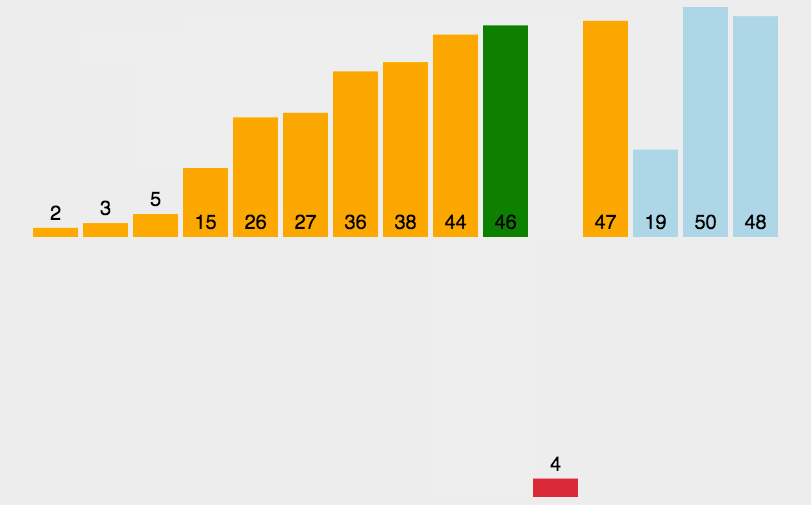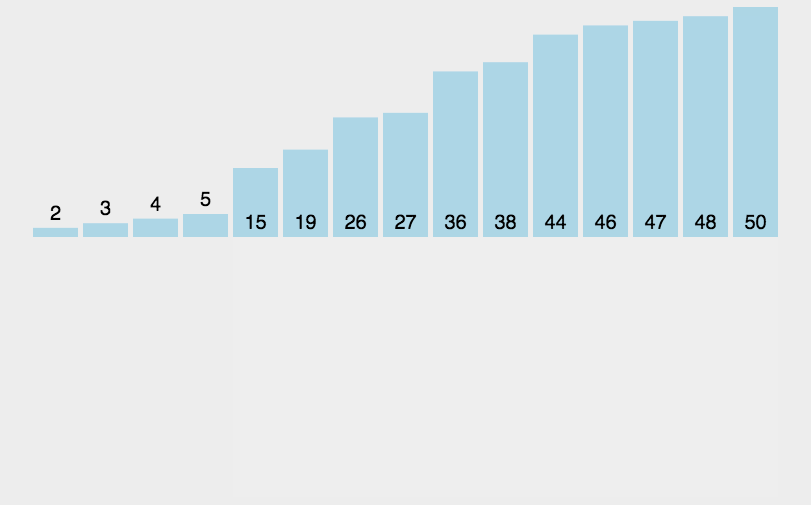
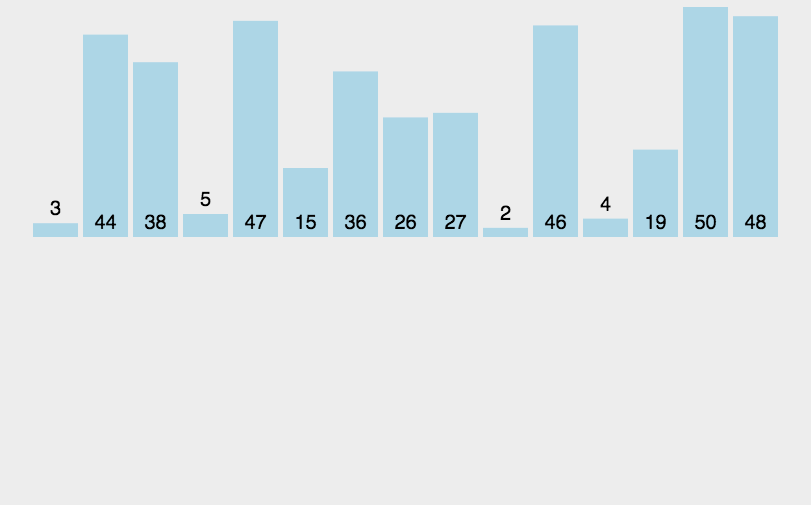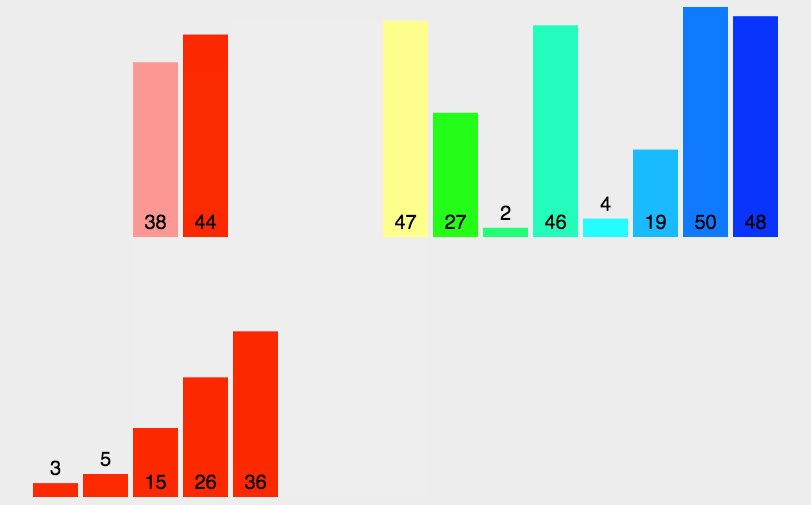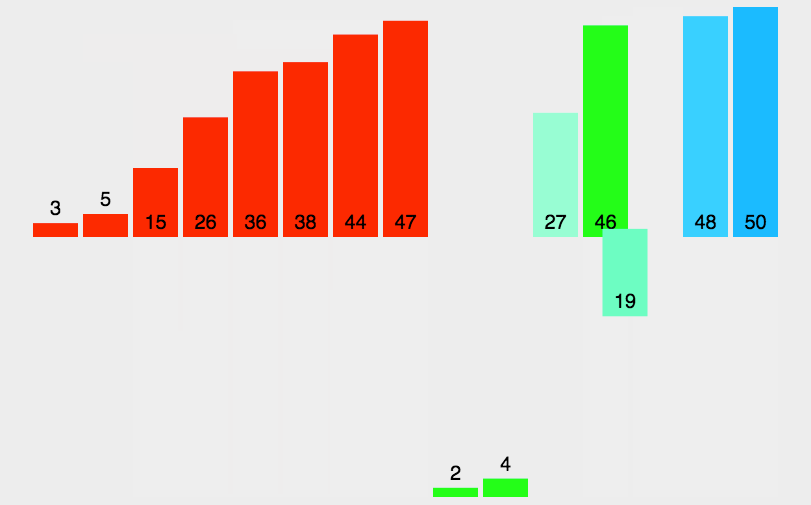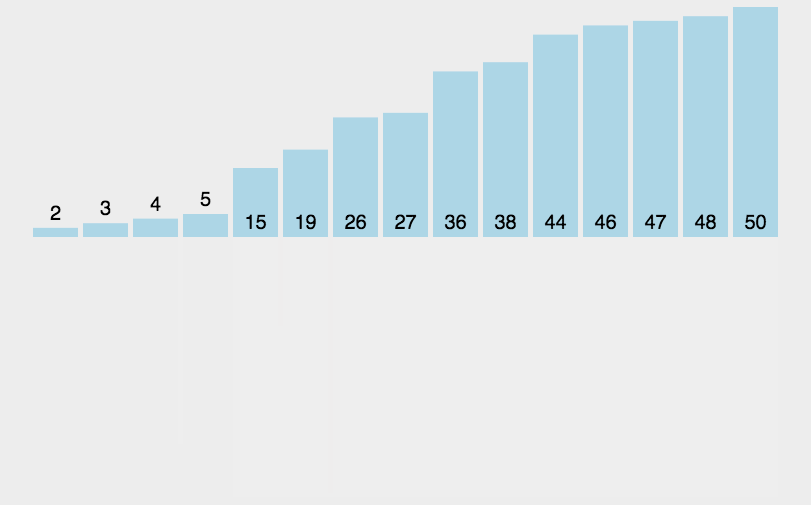
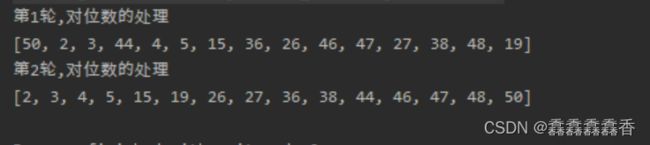
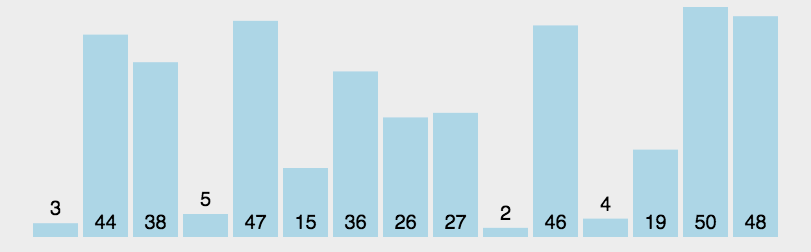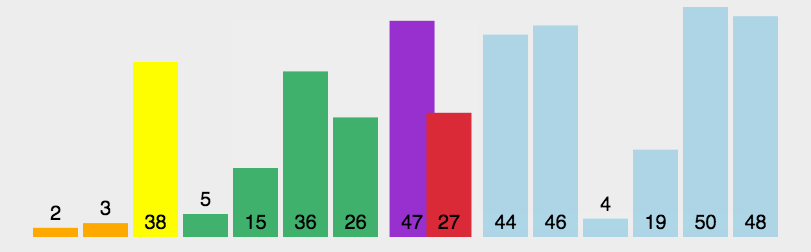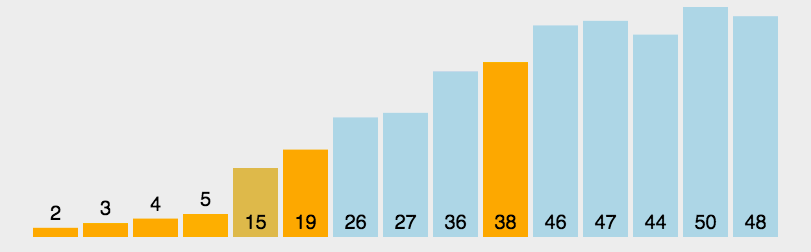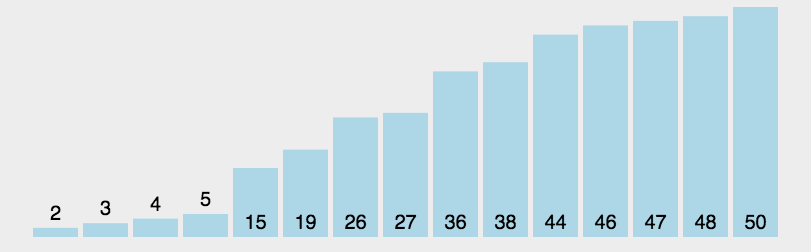
7.基数排序(桶排序)

(1)思路图解

将整数按位数切割成不同数字，然后按每个位数分别比较。
将所有待比较数值统一为同样的数位长度，数位较短的数前面补零。然后从最低位开始，依次进行依次排序。这样从最低到最高位排序完成之后，就得到一个有序序列。

(2)算法实现(java)

/**
 * 基数排序(桶排序)
 * author：xinxin
 */
public class BucketSort {
    public static void main(String[] args) {
        int[] arr = {3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};

        //找到最大的数
        int max = arr[0];
        for (int k = 1; k < arr.length; k++){
            if (max < arr[k]){
                max = arr[k];
            }
        }
        //最大的数位数是几位
        int maxLength = (max + "").length();
        
        //表示10个桶，每个一维数组都是一个桶
        int[][] bucket = new int[10][arr.length];

        //记录每个桶放入数据的个数
        int[] qty = new int[10];

        for (int l = 0,n = 1; l < maxLength; l++,n = n * 10) {
            //取对应位数数放进桶(第一次个位，第二次十位，第三次百位以此类推)
            for (int i = 0; i < arr.length; i++) {
                int bits = arr[i] / n % 10;
                //放到这个桶第一个位置，第二次放在第二个位置
                bucket[bits][qty[bits]] = arr[i];
                qty[bits]++;
            }

            //取出桶的数据放回原数组
            int index = 0;
            for (int j = 0; j < qty.length; j++) {
                if (qty[j] != 0){
                    for (int y = 0; y < qty[j]; y++){
                        arr[index++] = bucket[j][y];
                    }
                }
                //需要把桶归零
                qty[j] = 0;
            }
            System.out.println("第"+(l+1)+"轮,对位数的处理");
            System.out.println(Arrays.toString(arr));
        }

    }
}

运行结果

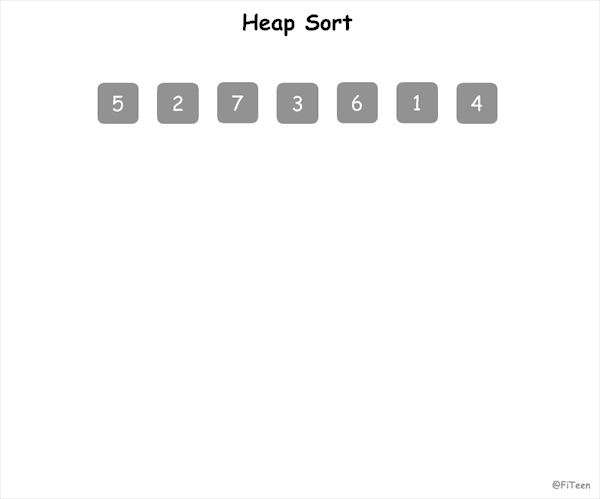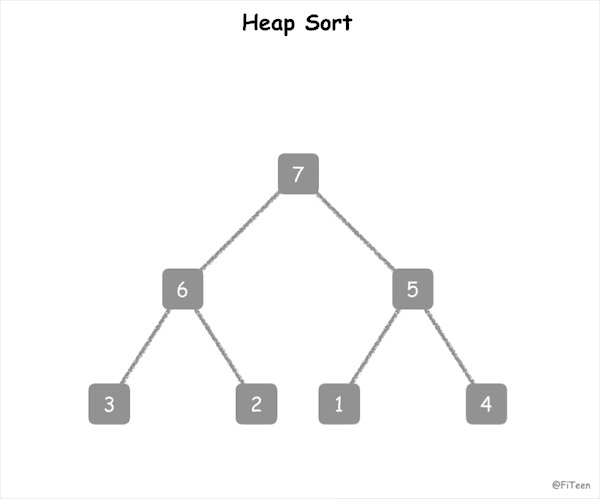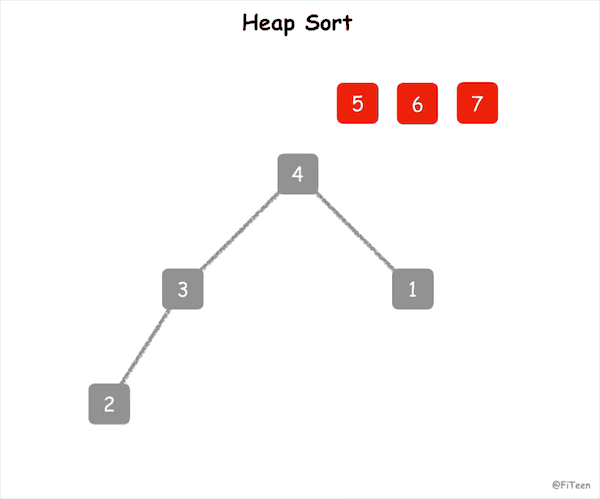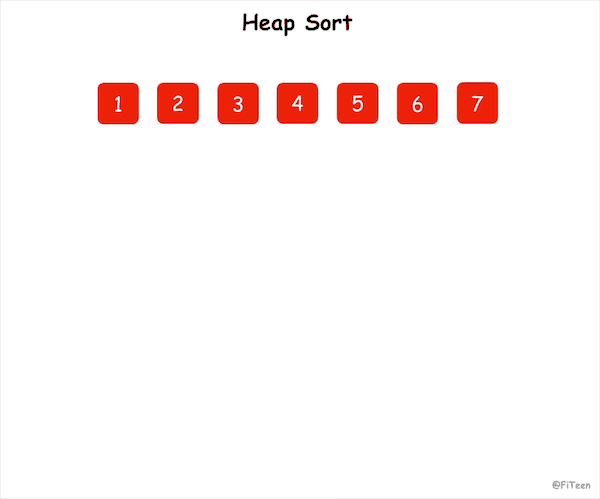
8.堆排序

(1)思路图解

将待排序序列构成一个大顶堆，最大值就是堆的根节点，将其与末尾元素交换，此时末尾就是最大值，然后剩余的元素重新构成堆，然后反复执行，最终形成一个有序序列。

(2)算法实现(java)

/**
 * 堆排序
 * author：xinxin
 */
public class HeapSort {
    public static void main(String[] args) {
        int[] arr = {5,2,7,3,6,1,4};
        int temp = 0;

        //使数组形成大顶堆
        for (int i = arr.length / 2 - 1; i >= 0; i--) {
            bigHeap(arr,i,arr.length);
        }

        //堆顶元素与末尾元素交换，使最大元素放在数组末端
        for (int j = arr.length-1; j > 0; j--) {
            temp = arr[j];
            arr[j] = arr[0];
            arr[0] = temp;
            bigHeap(arr,0,j);
        }
        System.out.println("堆排序结果");
        System.out.println(Arrays.toString(arr));
    }

    /**
     * 使待排序数组形成大顶堆
     * @param arr  初始数组
     * @param i    非叶子节点在数组中的下标
     * @param length 对多少个元素进行调整，length在减少
     */
    public static void bigHeap(int[] arr, int i, int length){
        int temp = arr[i];

        //i * 2 + 1是 i 的左子节点
      for (int k = i * 2 + 1; k < length; k = k * 2 + 1){
          //左子节点小于右子节点
          if(k + 1 < length && arr[k] < arr[k+1]){
              //指向右子节点
              k++;
          }
          //子节点大于根节点
          if (arr[k] > temp){
              arr[i] = arr[k];
              i = k;
          }else{
              break;
          }

          //把temp放在调整后的位置
          arr[i] = temp;
      }
    }
}

运行结果

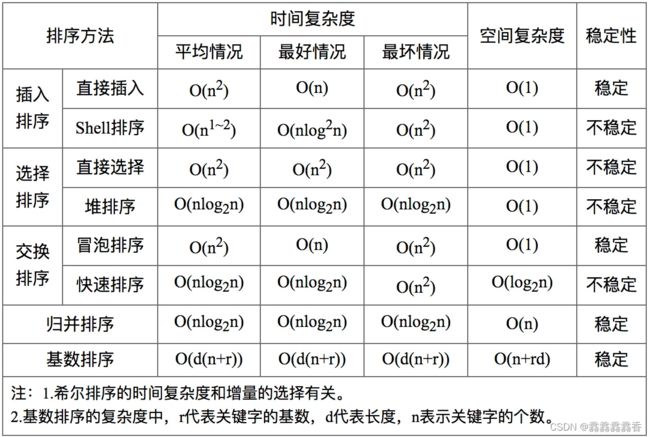
三.排序算法比较

shell排序是希尔排序

• 稳定

a原本在b前面，而a=b，排序之后a还在b前面。

• 不稳定

a原本在b前面，而a=b，排序之后a可能在b后面。

• 时间复杂度

算法执行需要的时间。

• 空间复杂度

算法运行需要的内存的大小。