哈希思想的简介、实现与深入

 

一、定义

    一个哈希组是满足下列条件的四元组(x,y,k,h):

        1) x是所有可能的消息的集合；

        2）y是由可能的消息摘要或认证标签构成的优先级，摘要即压缩后的数据；

        3）K 是密钥空间，是所有可能的密钥构成的有限集；

        4）对每个k ∈K, 存在一个哈希函数h: x->y;

 ͼK，存在一个hash函数hk ͼ H,hk:

x→yͼ

二、简介

     哈希的主要工作是将高维数据变为低维紧凑的二值码，即将复杂类型的数据用二进制串作为存储密码存储在计算机中，因此哈希表针对图像、视频或者文本数据库进行存储，实质是对原始数据的有损压缩。

     分类： 无监督哈希和有监督哈希；

     过程：key -> hash值 -> 桶号code ->存储；

     目的：让hash值均匀分布在桶中，使查找的消耗降到O(1)；

     优点：数据存储和查询消耗的时间大大降低；

     缺点：消耗比较多的内存;

三、常见哈希函数

     直接定址法

    1、除留余数法

         设哈希桶大小为m,取一个接近m的数p, hash(key) = key % p；

     随机数法

     折叠法

    数学分析法

    平方取中法

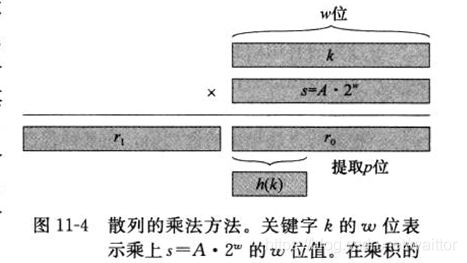
    2、乘法散列法

                                            hash(key) = floor( m * ((key *A) mod 1))

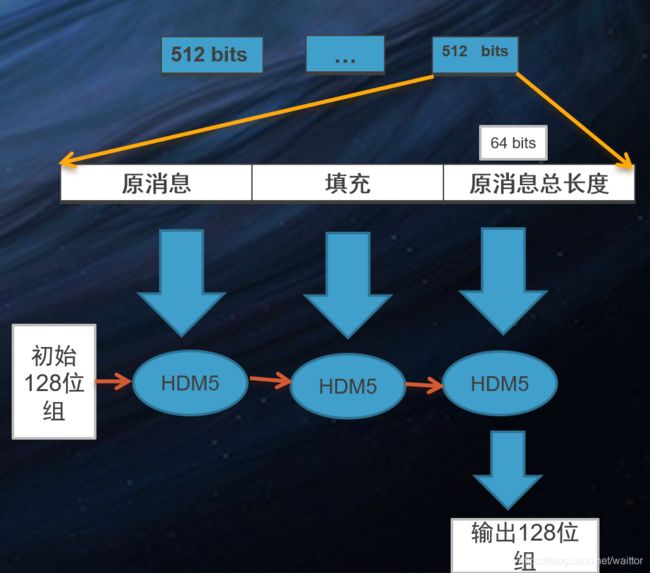
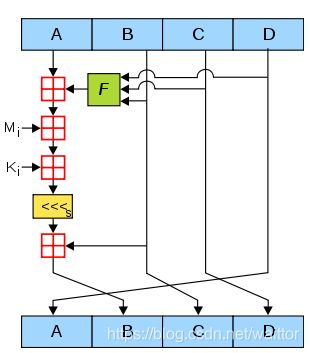
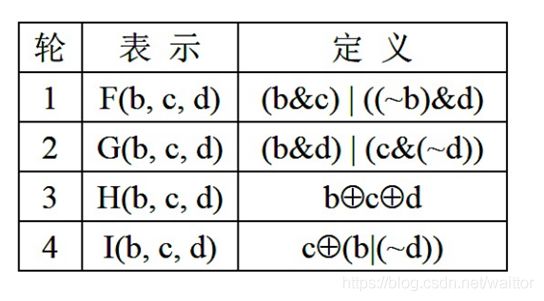
        设w为计算机字长,0

               取 s = A * 2w, key *s 为2w位数，前w位为整数部分，后w位为小数部分；

               再看上述散列，哈希函数的运算为取s的后w位的前几位为散列值。

    3、全域散列法

解释：

       为防范恶意存储数据到相同槽，哈希函数被设置为从哈希函数集中随机选取。

                                                 Data   ==>  {  hash_f1,hash_f2,hash_f3,…}  ===>  hashcode

一个常见方法：

        取 m 为素数，取随机数 A 为r+1位m进制数，表示为，

        将 key 转换为m 进制数，表示为 ,

        则哈希函数H[A](k)为：

                                                H[A](k) = sum { Ai * ki, i= 1,..m-1}  mod m

        结果为桶数组的槽数。

四、冲突处理方法

   1、开放寻址法

  1）线性检测

       以{12,15,4,5}为例

    2）二次检测

    3）双重散列     

hashcode = (h1(key) + i * h2(key)) mod m

   2、链地址法

        做法是在每一个表格(哈希桶)元素中维护一个list/queue/tree，然后我们在list/queue/tree上进行元素的插入和搜索删除等操作。虽然对list进行搜索是一种线性操作，但是只要list足够短，速度还是很快。

五、哈希函数性能评价

   评价标准：

      1) 正向快速--高效率、结果分布均匀;

      2) 逆向困难;

      3) 输入敏感，同时抗干扰强;

      4) 冲突避免;

   评价角度：

      1) 定址---创建时，能够快速有效地确定桶号

             e.g 除留余数法的取模运算时间

      2) 查找---取值时，能够准确快速地找到内容

             e.g 链接法查找时间与表的长度成正比

六、哈希函数的改进

1、取模运算优化

      除留余数法是最常用的哈希方法，但取模运算在计算机中的运算效率并不高，所以可以用以下操作代替：

                                        a % b = (b-1) & a,  当b（数组长度）为2的幂时等式成立

      JDK中的Hashmap采用的是这样的办法，也因此哈希桶的长度为2的幂。

2、位运算优化

      字符串哈希函数（如Time33算法）会遇到大量的数乘运算，可以使用加法和移位代替乘法提升效率：

                                                              Hash * 33 = hash + hash << 5

3、扩容

      当哈希表容量超过一定程度时，冲突会产生更多，冲突处理降低了哈希表的效率，这时需要对哈希表进行扩容。容量扩张是一次完毕的，期间要花非常长时间一次转移hash表中的全部元素。这样在hash表达到临界时，往里插入一个元素将会等候非常长的时间。

      1）扩容多少？

          通常为扩容为原来的2倍。当桶数组的长度为2的幂时，意味着不需要重新计算哈希值，而只是判断在原来哈希值的最高位是1还是0.即：

                                     new_hash = 1/0 + old_hash

      2）解决扩容带来的时间消耗 ---- 分摊转移

           声明一个新的扩容后的哈希表，每当增加一个新元素时，先将旧哈希表一个槽的所有元素转移到新哈希表，再计算该元素位置。

七、哈希思想的实现---MD5

   1. 主体描述

1) 输入：512 bits分组

2) 输出：128 bits消息摘要

3) 过程：

   a. 消息填充，补齐消息长度为模512时为448 ;

   b. 附加消息的长度值，在最后64位加上消息长度，消息总长度达到512的整数倍；

   c. 初始化消息摘要（MD）缓存器，128位组；

   d. 处理每一组的512位的报文分组

   e. 输出

  2. 迭代哈希函数HMD5 -- 思想：单向散列函数 干扰函数(待续)

HMD5由4轮运算组成，每轮16步，分别处理512/32=16个分组，经过64轮处理后，存储初始摘要的位置变为输出摘要。

过程：

    (1)对 A 迭代：a ← b + ((a + g(b, c, d) + X[k] + T[i]) <<

    (2)缓冲区 (A, B, C, D) 作循环轮换：(B, C, D, A) ← (A, B, C, D)

注：

    1）a, b, c, d : MD 缓冲区 (A, B, C, D) 的当前值；

     2）g : 轮函数 (F, G, H, I 中的一个)；

     3）<<

     4） X[k] : 32位子明文块；

     5）T[i] : 常数；

     6）“⊕”为模232操作，基于Davies-Meyer construction理论--- f(x, y) = Ey(x)⊕x

八、哈希思想的实现---通用模型(C)

接口文件hash.h

/* 功能：实现一个哈希函数的通用模型
 * 作者：waitor
 * 日期：20190514
 * 描述：使用单链表作为链地址法的数据结构
 * 备注：负载因子达到75%时未实现扩容，解决冲突的数据结构可以扩展为红黑树
 * */

#include 
#include 
#include 
#include 
// #include "myQueue.h"

// 哈希函数
typedef __uint32_t (*hash_code)(void *key);
//  冲突检测函数
typedef int (*compare)(void *key1, void *key2);

typedef struct hash_item hash_item_t;
struct hash_item
{
    void *key;
    void *value;
    hash_item_t *next;
};

typedef struct hash_map hash_map_t;
struct hash_map
{
    int size;            // 桶大小
    int capacity;        // 初始容量
    float loadFactory;   // 负载因子: 所占空间/总大小

    void *ths;           // 回调类型
    hash_code hf;        // 回调函数
    compare cf;          // 回调函数

    hash_item_t **map_struct; // 单链表数据结构
};

// 哈希表存储： 0--存储成功； -1 --存储失败，已存在
int hashmap_insert(void *key, hash_map_t *hashmap);
// 哈希表元素删除： 0--删除成功； -1 --删除失败，未找到
int hashmap_delete(void *key, hash_map_t *hashmap);
// 建立并初始化哈希表
hash_map_t *hashmap_new(int size, int capacity);
// 释放哈希表空间
int hashmap_release(hash_map_t *hashmap);
// 设置回调函数
void hashmap_set_hf(hash_map_t *hashmap, void *usr_data, hash_code hf);
// 设置回调函数
void hashmap_set_cf(hash_map_t *hashmap, void *usr_data, compare cf);

具体实现 hash.c 

#include "hash.h"

// 新建哈希表
hash_map_t *hashmap_new(int size, int capacity)
{
    hash_map_t *hashmap;

    hashmap = (hash_map_t *)malloc(sizeof(hashmap));
    hashmap->size = size;
    hashmap->capacity= capacity;

    hashmap->ths = NULL;
    hashmap->hf = NULL;
    hashmap->cf = NULL;
    hashmap->map_struct =(hash_item_t *)malloc(hashmap->size*sizeof(hash_item_t));

    return hashmap;
}

// 释放哈希表空间
int hashmap_release(hash_map_t *hashmap)
{
    hash_item_t *qn;
    hash_item_t *tmp;

    for(int i=0; isize; i++)
    {
        qn = hashmap->map_struct[i];
        while(qn) {
            tmp = qn->next;
            free(qn);
            qn = tmp;
        }
    }
    free(hashmap);

    return 0;
}

// 设置哈希回调函数
void hashmap_set_hf(hash_map_t *hashmap, void *usr_data, hash_code hf)
{
    hashmap->hf = hf;
    hashmap->ths = usr_data;
}
// 设置冲突检测回调函数
void hashmap_set_cf(hash_map_t *hashmap, void *usr_data, compare cf)
{
    hashmap->cf = cf;
    hashmap->ths = usr_data;
}

int hashmap_insert(void *key, hash_map_t *hashmap)
{
    __uint32_t hashcode;
    hash_item_t *qn;
    
    hashcode = hashmap->hf(key);
    qn = hashmap->map_struct[hashcode];
    while(qn->next) {
        qn = qn->next;
        if(hashmap->cf(qn->key, key) == 1) {
            printf("已存在\n");
            return -1;
        }
    }
    qn->next = (hash_item_t *)((void*)((char*)key-offsetof(hash_item_t,key)));

    return 0;
}

int hashmap_delete(void *key, hash_map_t *hashmap)
{
    __uint32_t hashcode;
    hash_item_t *qn;

    hashcode = hashmap->hf(key);
    qn = hashmap->map_struct[hashcode];
    while(qn->next) {
        if(hashmap->cf(qn->next->key, key) == 1) {
            hash_item_t *tmp = qn->next->next;
            free(qn->next);
            qn->next = tmp;
            return 0;
        }
        qn = qn->next;
    }
    printf("未找到\n");
    return -1;
}

测试demo

#include "hash/hash.h"

__uint32_t hashcode(char *str)
{
    __uint32_t code = 5381;
    while(*str) {
        code = (code << 5) + code + *str++;
    }
    return (code & 0x7FFFFFFF);
}

int compare(char *str1, char *str2)
{
    while(*str1)
    {
        if((*str1++) != (*str2++))
            return 0;
    }
    return 1;
}

int main() {

    hash_map_t *hashmap;

    hashmap = hashmap_new(10, 100);
    hashmap_set_hf(hashmap, NULL, (hashcode)hashcode);
    hashmap_set_cf(hashmap, NULL, (compare)compare);
    
    hashmap_release(hashmap);

    return 0;
}

参考资料

  《算法导论第三版》

  《算法笔记》

  《Sorting and Searching, Volume 3 of The Art of Compute Programming》;

  《Handbook of Algoruthms and Data Structures》;

  《Dynamic perfect hashing :Upper and lower bounds 》;

    Coron, J.-S., Dodis, Y., Malinaud, C., & Puniya, P. (2005). Merkle-Damgård Revisited: How to Construct a Hash Function.