例题
买不到的数目

这道题目通过打表找规律,得到答案为(n-1)*(m-1)-1,然后直接输出答案即可,下面附上打表代码和ac代码(打表是找规律的一种好的方法)
性质:两个互质的数p和q,最大不能表示的数为(p-1)*(q-1)-1
打表代码:
#include
#include
#include
#include
#include
#include
ac代码:
#include
#include
#include
#include
#include
#include
蚂蚁感冒

输入样例1:
3
5 -2 8
输出样例1:
1
输入样例2:
5
-10 8 -20 12 25
输出样例2:
3
这道题需要发现一个特点,就是蚂蚁与蚂蚁之间其实是没什么区别的,也就是说两个蚂蚁碰头之后转身继续行走相当于直接穿过对方的身体,知道了这个性质之后这道题目就比较好想了,举一个简单的例子,假如一开始蚂蚁是向右走的,首先他初始位置右边且向左走的蚂蚁都会被传染,那他左边向右走的蚂蚁呢?这个时候就要看看是否存在他右边且向左走的蚂蚁了,如果有的话就会被传染,否则就不会,如果一开始蚂蚁是向左走的也是一样的分析方式
代码:
#include
#include
#include
#include
#include
#include
饮料换购
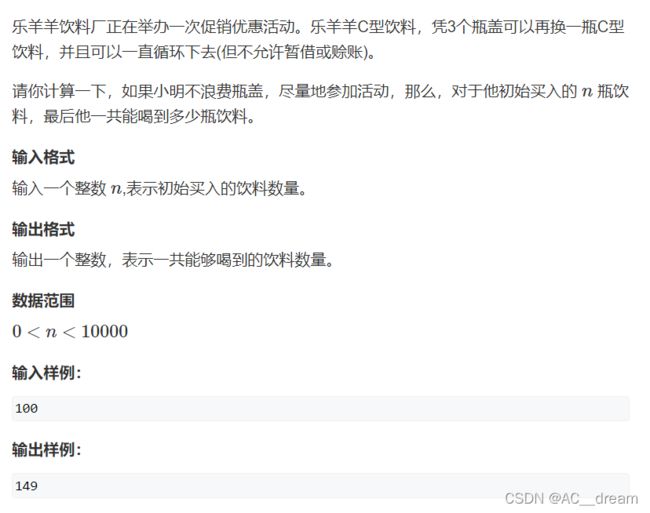
这个直接按照题意模拟就行,终止条件就是当前瓶盖数小于3.详情见代码
代码:
#include
#include
#include
#include
#include
#include
背包问题
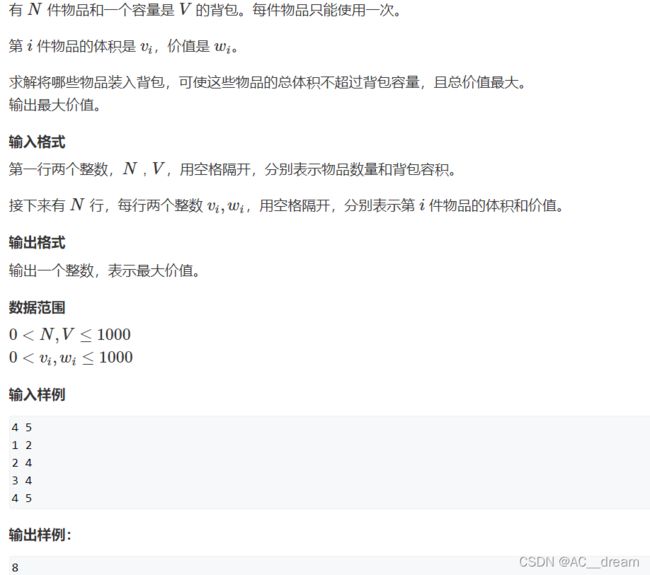
常见的背包问题我在之前博客种有过详细介绍,可以参考下之前博客常见背包问题_AC__dream的博客-CSDN博客
#include
#include
#include
#include
#include
#include
摘花生


这道题目是一个递推题,我们从左下到右上依次递推,走到当前格子所能获得的花生的最大数量等于当前格子的花生数量加上当前格子上面一个格子和左面一个格子的最大值,就这样最后输出终点坐标处所能获得的最大花生数量即可
代码:
#include
#include
#include
#include
#include
#include
最长上升子序列
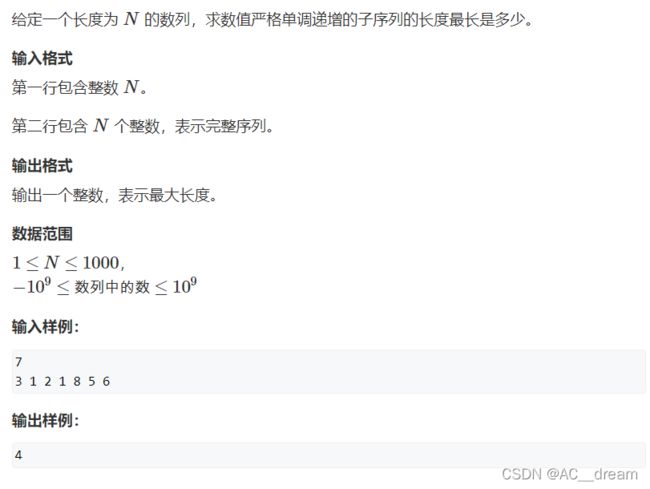
最长子序列问题我在之前博客中有详细介绍,详情可以参考之前博客最长子序列问题_AC__dream的博客-CSDN博客d
代码:
#include
#include
#include
#include
#include
#include
习题
地宫取宝

输入样例1:
2 2 2
1 2
2 1
输出样例1:
2
输入样例2:
2 3 2
1 2 3
2 1 5
输出样例2:
14
这道题目我们主要用动态规划来解决,是前一道题的进阶版,就是在前一道题的基础上加了一些限制条件,dp[i][j][k][l]表示当前在(i,j)这个点已经选取了k个物品,k个物品中的最大值是l的方案数,这样我们就可以根据题意进行正常递推了,但是有一个坑就是宝贝的价值是从0开始的,由于我们每次选宝贝都要比之前选的宝贝价值大,而我们初始状态下默认已选择的宝贝的最大值为0,这样就导致我们在更新过程中无法选择价值为0的宝贝,所以我们一开始应将所有的宝贝价值加1,让宝贝的价值从1开始就可以了,细节见代码
#include
#include
#include
#include
#include
#include
波动数列
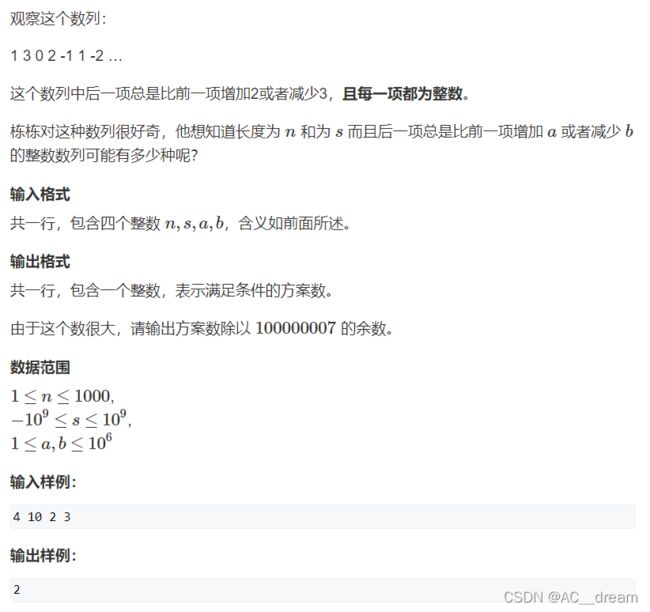
s=n*x+(n-1)d1+(n-2)d2+…+d(n-1)
则 (n-1)d1+(n-2)d2+…+d(n-1)与s模n同余,那我们只需要枚举每次选择的公差并进行递推即可
dp[i][j]记录只考虑前i个公差的选择,(n-1)d1+(n-2)d2+…+(n-i)di对n的余数
则递推式即为 dp[i][j]+=dp[i-1][((j-t1)%n+n)%n],dp[i][j]+=dp[i-1][((j-t2)%n+n)%n],t1和t2是公差的倍数
代码:
#include
#include
#include
#include
#include
#include








