在武测学习（一）：神经网络入门——《Python深度学习》学习笔记

目录

1 神经网络入门

1.1 机器学习、深度学习与神经网络

1.1.1 机器学习

1.1.2 深度学习与神经网络

1.1.3 深度学习的特别之处

1.2 全连接神经网络

1.2.1 二分类问题——IMDB中的电影评论

1.2.2 多分类问题

1.2.3 标量回归问题

1.3 用Pytorch实现全连接层

1.3.1 定义dataset和dataloader

1.3.2 定义模型类 

1.3.3 训练模型

1.4 小结

---

大二这一年，身边同学多多少少都开始紧张了起来，于是一边卷着必修课的分数，一边参加各种竞赛。我一向对周围反应有些迟缓，但在上学期也开始有些焦虑，感到和优秀同学的距离越来越远，又苦于身边没有可靠的信息源，对竞赛更是一无所知。只好先从成绩做起。

所幸上学期成绩尚可，为了不让自己有太多偷懒的空间，随大流报了两项测绘技能大赛和数模国赛（校内选拔）。虽然最后仅有程序设计比赛得到一个不尽人意的奖项，而且过程中一直走弯路，但实际上那段时间是我找到学习状态的开始。

今年的评奖评优已经结束，拿到了国家奖学金，数模也推送了国奖，不得不说我是有点运气在身上的，毕竟这些结果我从来都没有想过。这学期开始，又觉得应该进一步做些什么，至少延续一下上学期的状态。

于是找到老师聊天，希望可以在课程之外有所拓展。我不希望自己抱着要发一篇论文或者参加一个比赛来取得保研加分的心态去做这件事。和一个导航的同学聊过，他远比我厉害，但是大二没有好好学，而且导航竞争激烈，导致排名并没有那么理想。他说想要稳住保研资格，然后学自己真正想学的东西。这点上我同他一样，本科四年已过半，这段学习过程中，时常能真切地感受到一种无所不在的拘束感，就是得时时刻刻被各种“评价体系”牵着走——综测需要活动分，就去搞各种活动，参加社团；保研需要科研分，就去申专利，打比赛，发论文；秋招需要实习经验，就去到处找实习。我从没想过大学是这样的。好像所有人都追逐一样的东西。

对于摄影测量的几个方向，我其实都很有很大兴趣。但肯定是得选一个的，毕竟精力有限。选择AI方向是觉得应用场景会更丰富，另一方面也是和计算机沾边一些，而且对模式识别方面的内容也比较好奇。加上参加了数模，多少会有一些了解。

这个系列将会记录我大三开始的学习历程，可能进度比较慢，因为最近发现课程内容远比想象的多

---

 

1 神经网络入门

1.1 机器学习、深度学习与神经网络

数模期间耳朵都听烂的几个名词（相信很多同学都是)：机器学习、深度学习、神经网络。在我能够比较熟练调用机器学习的工具包之后，我依然没有搞明白各自具体的内容，更别说它们之间的关系了。书中对这部分内容有充实的篇幅，并且写得非常浅显生动。

1.1.1 机器学习

机器学习的目的是为数据寻找一种有意义的表示方法。

如何看待这个“表示方法”的含义？借用书上的例子：

若在平面内有一系列点，分为白点和黑点，现在的目标是将其分类。

原始数据

肉眼看过去，可以借助一条曲线来完成这个任务：曲线之上为黑点，之下为白点。

但这样一条曲线该如何表示？我们几乎不可能用函数解析式表示它，而且这样的曲线有无数条，又要怎么选择？

首先要解决他的表示问题，假设存在一种变换F：

能够使得变换后的点变成更易于分类的模式，如下图中，横坐标大于0就是黑点，横坐标小于0就是白点。

更好的数据表示

这样分类就变成了极其简单的问题，因此这是一个更好的数据表示——当然仅仅是对于这个问题而言。机器学习的任务，实质上就是系统性地、自动地搜索这个变换方法F。它的形式需要人为去定义，例如线性变换、旋转平移以及各种叠加。很显然，类似于其它搜索算法，它也需要一个反馈信号，来告诉它下一步如何去走。对于不同的问题也就有不同的反馈信号，在这个问题中，可以设置为分类的正确率。

但是有一个问题：在训练过程中我们使用了“已知”的黑点和白点坐标，而黑和白是两个类别，无法保证所有的黑点坐标经过变换后都可以落在Y轴右边，白点亦然。而对于实际应用，我们更希望得到一个“普适”的数据表示。因此必须预留出一部分数据不参与训练，使模型“不知道”这部分数据，然后利用它来检验模型的性能。这就是验证集。提升在已知数据之外的表现，也提醒了我们需要从无穷多个变换中找到比较合适的一个。

1.1.2 深度学习与神经网络

深度学习是机器学习的分支。它强调从连续的层（layer）中进行学习。深度学习中的“深度”表示层的个数，与其它机器学习方法的区别就在于它使用了更多的层。

神经网络严格意义上并没有完全被深度学习所包含，可以理解为深度学习的主要表示方法。

层的含义就和之前所说的变换F相似。多个层实际就是多个变换的叠加，以此来实现较为复杂的变换。层的本质是对数据的一次操作或者说变换，因此层一定由某些参数来决定，这个参数就是权重。而学习的目的就转换为为这些层寻找一个合适的权重。

如前所述，需要一个反馈信号来修正权证，通过损失函数（loss function）来得到。函数的变量是模型得出的预测值和真实值。

接下来观察损失函数得到的损失值，从而调整层的权重。这一步借助优化器（optimizer）来完成，原理是反向传播。这是个名字很高级，但原理却很简单的算法，实际上就是复合函数的求导。

可以看出，深度学习的机制非常简单，接下来的任务，就是构建更适合问题的模型，以及对模型进行训练。

1.1.3 深度学习的特别之处

其它的机器学习层级很少，如支持向量机和决策树算法，往往无法解决复杂空间里的问题，必须通过特征工程来改善原始数据（手动寻找一种比较好的数据表示方法）。而深度学习将这一过程自动化，可以一次性就学到所有的特征，无需人为干预，也就是一个端到端的模型。

并且深度学习多层堆叠的效果不能由多次浅层学习来替代。因为每次浅层学习都是当前的最优特征，而深度学习是对所有特征共同学习，每一层之间都有相关性。

归纳深度学习的特征为两点：

• 通过渐进的、逐层的方法方式形成越来越复杂的表示
• 对中间这些渐进的表示共同进行学习

1.2 全连接神经网络

神经网络之间的区别无非在于层的结构和类型。最简单的神经网络就是全连接神经网络，即所有的层都是Dense层。它可以解决许多简单问题。书本中给出了三种常见问题——二分类、多分类以及标量回归——并分别用全连接神经网络进行了实践。在这一章中能够了解到神经网络的基本工作方式。

神经网络的输入数据是张量（tensor），也就是多维矩阵数组。0D的张量称为标量（scalar），1D的张量称为向量（vector），2D张量称为矩阵（matrix）。深度学习处理的一般是0D到4D的张量。

因此搭建一个神经网络之前，需要根据具体需求，明确输入输出的形式（张量的尺寸和数据类型）。对于二分类问题，我们希望得到“0”或“1”的结果，对于多分类问题，就变成一串二进制码；而对于标量回归，则需要得到一个具体的数值。对应于不同的任务，输入张量的维度可能不同，输出的结果亦然，并且往往各自有效果比较好的激活函数和损失函数。

1.2.1 二分类问题——IMDB中的电影评论

首先导入数据。num_words=10000能够实现仅保留前10000个最常用单词。

#导入IMDB数据集，train_labels对应于每条评论的类别（标签）
from keras.datasets import imdb
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)

在IMDB数据集中，train_data是一个列表（List）类型，包含50000条数据，每条数据是一个整数序列，并且长度不一。Dense层只能处理浮点数向量数据，因此需要先将数据转换成张量。对于这种整数序列，可以采用Embedding层进行词嵌入，也可以使用one-hot编码将其处理成0和1的序列，这里先对one-hot编码做介绍。

one-hot编码需要知道数据的范围。对于此问题，数据范围很显然是0~9999（保留了前10000个常用单词），因此可以用一个长度为10000的向量来表示一个sentence，例如一句话是[3,5,6]，那么编码后就变成1×10000的向量，其中第3,5,6项为1，其余为0。这样编码能够保证向量长度相同。

但是这样编码很显然会失去单词的顺序信息，但从作者的表述来看，词语的顺序对情感判断似乎影响不大。如果要保留顺序信息，可以对文本进行截取，也就是确定一个len_sentence，让每一个sentence转变为len_sentence×num_words的二维张量，然后再展平。但这样做的计算量会大大上升。就这个例子而言并没有必要。

import numpy as np

#定义函数
def vectorize_sequences(sequences, dimension=10000):
    #创建对应大小的零张量
    results = np.zeros((len(sequences), dimension))
    #遍历每一个sentence，对对应的行进行赋值
    for i, sequence in enumerate(sequences):
        results[i, sequence] = 1.  
    return results

#调用函数
x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)

这里定义了函数vectorize_sequences(sequences, dimension=10000)，首先建立对应大小的零矩阵，然后遍历对其赋1值。

这里使用了enumerate函数，在后面的数据处理中非常常见。它能同时获取列表中数据的索引值i和数据值，因而使用起来十分便利。例如这里得到i和sentence之后，直接就可以对result中的第i行进行赋值，大大简化了代码。

同样地，标签也需要向量化。标签的长度是统一的，因此只需要转换一下数据类型，利用np.asarray函数即可。

#asarray将List转换为ndarray数组，astype定义其数据类型
y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')

数据准备完成，就可以开始搭建全连接层了。首先定义一个新的模型。

from keras import models
from keras import layers

model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

Dense层的定义主要是输出大小，激活函数以及输入大小。输出大小也就是隐藏单元的个数，是Dense的维度。在第一层Dense层还需要定义输入数据的形状input_shape，之后的层就不需要了，网络会自动计算。

中间每一层的激活函数都选用relu，最后一层选择sigmoid。

relu是一个max（x，0）的函数，其目的是像变换中增加非线性成分，否则每一层都是线性变换，就没必要搭那么多层了。

而sigmoid函数能够将任意值压缩到0~1之间，可以将其输出值看作概率值：0或1的概率。

因此该模型实现了一个长度为10000的向量的输入，和长度为1的0~1之间数字的输出。

这里无需操心输入的数据有几条，Dense只需要定义一条数据的长度即可，无论几条数据同时输入都可以处理，

下一步是编译模型，这一步为需要为模型定义优化器（optimizer）和损失函数（loss），还可以自己加上监控变量（metrics）。

model.compile(optimizer='rmsprop',
              loss='binary_crossentropy',
              metrics=['accuracy'])

但这种字符串定义的方式无法配置优化器具体的参数，因此更建议定义优化器类实例。

from keras import optimizers

model.compile(optimizer=optimizers.RMSprop(lr=0.001),
              loss='binary_crossentropy',
              metrics=['accuracy'])

对于输出结果为概率值的情况，交叉熵（crossentropy）往往是最好的选择。因此损失函数选择binary _crossentropy。优化器的话，一般RMSprop都可以胜任。

到这里还不能直接开始训练，因为之前提到的过拟合的问题：如果在所有训练集上训练，模型很快会完美地适应整个数据集，达到百分百的精度，但这样的结果在测试集上表现会很糟糕。所以需要在训练集中划分出一部分来，作为验证集。通过验证集，可以在训练过程中看到模型是否过拟合。

#留出前10000条数据作为验证集
x_val = x_train[:10000]
partial_x_train = x_train[10000:]

y_val = y_train[:10000]
partial_y_train = y_train[10000:]

代码中的方法称为留出验证，在数据集丰富的情况下是合理的。如果数据集并没有那么多，则需要用到K折交叉验证，在后面会详细说明。

当用到验证集的时候，模型编译结果存在一个History类实例里，包括训练集精度和验证集精度，便于绘图查看。

history = model.fit(partial_x_train,    #训练集
                    partial_y_train,
                    epochs=20,          #迭代轮次
                    batch_size=512,     #批量大小
                    validation_data=(x_val, y_val))  #验证集

在每一轮次的计算中，模型不断输入batch_size个数据，直到所有数据都输入，这个过程经历[num_examples/batch_size]次，而模型的输出也会显示这个数字。epochs则定义了总共的轮次数。

接下来绘制测试精度和验证精度的图。其中history类中包含了一个history变量，它是一个字典，存储了精度值和损失值。

import matplotlib.pyplot as plt
#准备数据
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
#定义横坐标
epochs = range(1, len(acc) + 1)
#绘图
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()

plt.show()

这里由于版本问题，字典里对精度值的索引可能不是acc，因此可以事先查看一下字典中包含的字段名称：

history_dict = history.history
history_dict.keys()

得到的显示结果为

dict_keys(['loss', 'accuracy', 'val_loss', 'val_accuracy'])

 因此修改代码中acc为accuracy：

#准备数据
acc = history.history['accurracy']
val_acc = history.history['val_accurracy']
loss = history.history['loss']
val_loss = history.history['val_loss']

继续绘制精度图像 

plt.clf()   #清空图窗

plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()

plt.show()

得到两幅图像：

在训练前几个轮次时，训练损失和验证损失一起下降，当第4轮过后验证损失开始向上走，而训练损失越来越少，这就是典型的过拟合。

精度图像呈现同样的现象，只不过曲线方向反过来。

因此借助验证集，可以大概确定训练的最佳轮次是4轮（对于目前的参数而言），接下来就可以使用全部数据重新训练模型，让它在第四轮停止，模型也就训练完成了。这里对训练轮次的优化，实际上就是超参数的一种选择。超参数不能被网络自己学习到，需要人为去调整。

重新训练模型：

model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

model.compile(optimizer='rmsprop',
              loss='binary_crossentropy',
              metrics=['accuracy'])

model.fit(x_train, y_train, epochs=4, batch_size=512)

#计算模型在测试集上的精度
results = model.evaluate(x_test, y_test)

重新训练后，调用evaluate函数，计算出的result包含和训练一样，包含损失值和精度值

[0.299601286649704, 0.8816800117492676]

模型达到88%的精度。

要用模型来预测，则使用predict方法。

书上给出了一些可能可以提高模型精度的方法：改变Dense层的个数、改变Dense层中隐藏单元的个数，改变损失函数和激活函数等等。

从我一开始的直觉看来，更多的层应当对应更好的学习能力，而且我对原始代码中从10000直接降维到16也表示怀疑。但我试验之后并没有取得更好的结果。后来更多事实也会证明神经网络的结果可能会有悖于我们所习惯的一些常识。

改变激活函数为tanh也并没有改善网络，基本得到的结果没有太大差别。不过能够看到的结论是：

• 非常少的层意味着不容易过拟合，而增加层数可能导致从第一轮就过拟合。层数并不是越多越好，隐藏单元也是。
• relu激活函数简单但是却非常有效

我比较好奇的是为什么作者喜欢把参数设置成诸如16,512这样的2的次方数，也许更适合计算计算机处理？但batchsize照理说和这个也没什么关系。也许是个人习惯吧。

1.2.2 多分类问题

在有上述模型的基础上，对于另外两种问题就只关注它们的主要区别了，代码网上也都是有的。

多分类问题的输出将会是一个向量。参照二分类问题，它应该是一串在0到1之间的数字，表示每一种类别的概率。

在文章中的路透社数据集里，数据集标签是一个0~45范围的整数，表示类别，因此可以采用one-hot编码将其转换为长度为46的0-1序列。

keras内置了to_categorical函数，可以直接对整数序列进行one-hot编码，但它只接受类别向量，也就是label这样的向量，不能用于x_train的编码。

接下来构建网络。主要的改变有：

• 由于需要学会46种类别，因此Dense层的隐藏单元数需要更多。
• 另外，在最后一层的激活函数变为了softmax，这个激活函数可以让输出向量元素之和为1，也就是一串概率值。
• 损失函数变为categorical_crossentropy（分类交叉熵）。它通过计算求得的概率分布和真实概率分布之间的距离来改善网络。

最终预测得到的向量，可以通过np.argmax来获取每一行的最大值的索引，作为概率最大的类别。

1.2.3 标量回归问题

回归问题和分类问题的区别在于所得到的结果是一个连续值。

准备数据阶段：波士顿房价数据集中，每个样本有13个特征，包括各种数据，所以数据大小差别很大。为了让神经网络更容易学习，一般需要对数据做标准化。

mean = train_data.mean(axis=0)
train_data -= mean
std = train_data.std(axis=0)
train_data /= std

test_data -= mean
test_data /= std

值得一提的是，这里在计算均值和标准差时，只用了训练数据。哪怕对测试数据操作时也是如此。这和后面书中所提到的信息泄露类似，就是无论如何也不能讲测试数据中任何信息透露给模型。这并不难理解。

由于测试数据较少，需要使用之前提到的K折验证。

K折验证原理很简单，就是将数据集均匀划分成K份（划分之前可以打乱或者不打乱），然后以其中K-1个集合为训练集，另一个为验证集进行训练。重复这样的操作K次，将所得的验证精度和验证损失求平均，就得到了K折验证精度和验证损失。

为了查看模型过拟合情况（验证分数随轮次发生的变化），可以将所有的mse或mae存储下来，这里需要借助history。因此我个人觉得用history去fit是最好的方法，便于之后查看轮次对模型的影响。

具体代码如下：

from keras import models
from keras import layers
import numpy as np

#定义模型初始化和编译的函数，方便在K折验证过程中调用
def build_model():
    # Because we will need to instantiate
    # the same model multiple times,
    # we use a function to construct it.
    model = models.Sequential()
    model.add(layers.Dense(64, activation='relu',
                           input_shape=(train_data.shape[1],)))
    model.add(layers.Dense(64, activation='relu'))
    model.add(layers.Dense(1))
    model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
    return model

#K折验证
k = 4
num_val_samples = len(train_data) // k
num_epochs = 500
all_mae_histories = []            #储存所有的验证分数

#循环验证
for i in range(k):
    print('processing fold #', i)
    #划分验证集（第i个集合）
    val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
    val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]

    #拼接训练集
    partial_train_data = np.concatenate(
        [train_data[:i * num_val_samples],
         train_data[(i + 1) * num_val_samples:]],
        axis=0)
    partial_train_targets = np.concatenate(
        [train_targets[:i * num_val_samples],
         train_targets[(i + 1) * num_val_samples:]],
        axis=0)

    #初始化模型
    model = build_model()
    #训练模型
    history = model.fit(partial_train_data, partial_train_targets,
                        validation_data=(val_data, val_targets),
                        epochs=num_epochs, batch_size=1, verbose=0)
    #verbose=0表示静默模式，命令行不会有输出

    #添加数据
    mae_history = history.history['val_mae']
    all_mae_histories.append(mae_history)

#取平均：x表示某一“行”，i表示某一“列”
average_mae_history = [
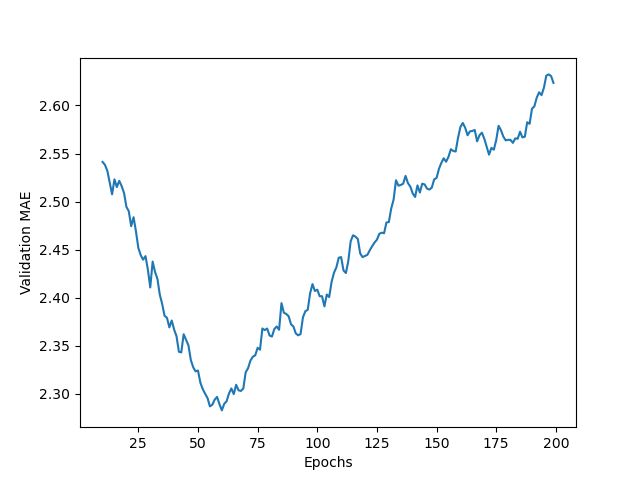
    np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]

绘制得到图像如下 

最后对每一轮次的K个值求平均，绘图输出。Verbose等于0可以取消输出，但是输出里包含不少有用的信息，例如history索引可以直接在输出中看到，因此个人觉得没太大必要设置成静默模式。

输出的结果可能波动会比较大，为了更容易看出过拟合的节点，可以去掉比较特殊的值，然后对曲线做指数移动平均。具体方法不再赘述，代码里写得很清楚。

#定义曲线平滑函数，factor为因子，表示平滑程度
def smooth_curve(points, factor=0.9):
  smoothed_points = []
  for point in points:
    if smoothed_points:
      previous = smoothed_points[-1]
      smoothed_points.append(previous * factor + point * (1 - factor))
    else:
      smoothed_points.append(point)
  return smoothed_points

#调用函数（只取10轮次以后的数据）
smooth_mae_history = smooth_curve(average_mae_history[10:])

#绘制图像
plt.plot(range(10, len(smooth_mae_history) + 10), smooth_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()

原文代码没有移动X轴的范围，这里做了调整。可以看到，模型在60轮左右开始过拟合。

和之前一样，可以开始训练最终的模型了

model = build_model()
#用所有的训练集进行训练
model.fit(train_data, train_targets,
          epochs=60, batch_size=16)
#计算分数
test_mse_score, test_mae_score = model.evaluate(test_data, test_targets)

 预测的房价和实际价格差2540美元，比书本上要好10美元，哈哈

1.3 用Pytorch实现全连接层

由于我的显卡不支持pytorch，只好先安装了CPU版本的pytorch，对于简单的代码够用了。

下面主要对pytorch和keras的构建方法以及模型构建和参数调整的方式做一些对比，。

1.3.1 定义dataset和dataloader

在pytorch中准备数据，基本的数据类型是tensor张量，和ndaray可以互相转换。

对数据进行处理后，还需要定义dataset和dataloader。

一般对训练数据定义train_loader，通过两个参数：数据集和batchsize

# 将训练数据转换为dataset
train_data=Data.TensorDataset(x_train,y_train)
# 通过dataset定义训练数据生成器
train_loader=Data.DataLoader(dataset=train_data,batch_size=64)

1.3.2 定义模型类 

 这一段代码的结构基本都类似，包括构造函数__init__(self)和前向传播函数forward(self,x)

（*在pytorch类的函数定义中，默认第一个参数为self。通过对self的各个参数进行设定，从而构建神经网络模型。其指代的是实例类本身，和C语言中的this类似）

构建的思路和keras中的API类似，同样很直观。具体见代码注释。

class model(nn.Module):

    #__init__(self)方法在类实例化时自动执行
    #可以类比为构造函数，一般将模型结构的定义写在其中
    def __init__(self):

        #super方法可以让self继承父类model的初始特性
        #通常都会作为第一句出现
        super(model, self).__init__()

        #定义隐藏层，Linear表示线性运算，也就是keras的Dense层
        self.hidden=nn.Sequential(
            nn.Linear(30,20),
            nn.ReLU(),
            nn.Linear(20,10),
            nn.ReLU()
        )

        #定义分类器，也就是最后一层
        self.classifier=nn.Sequential(
            nn.Linear(10,2),
            nn.Sigmoid()
        )

    #定义向前传播函数
    def forward(self,x):
        x=self.hidden(x)
        x=self.classifier(x)
        return x

print（model）可以看到模型的结构

model(
  (hidden): Sequential(
    (0): Linear(in_features=30, out_features=20, bias=True)
    (1): ReLU()
    (2): Linear(in_features=20, out_features=10, bias=True)
    (3): ReLU()
  )
  (classifier): Sequential(
    (0): Linear(in_features=10, out_features=2, bias=True)
    (1): Sigmoid()
  )
)

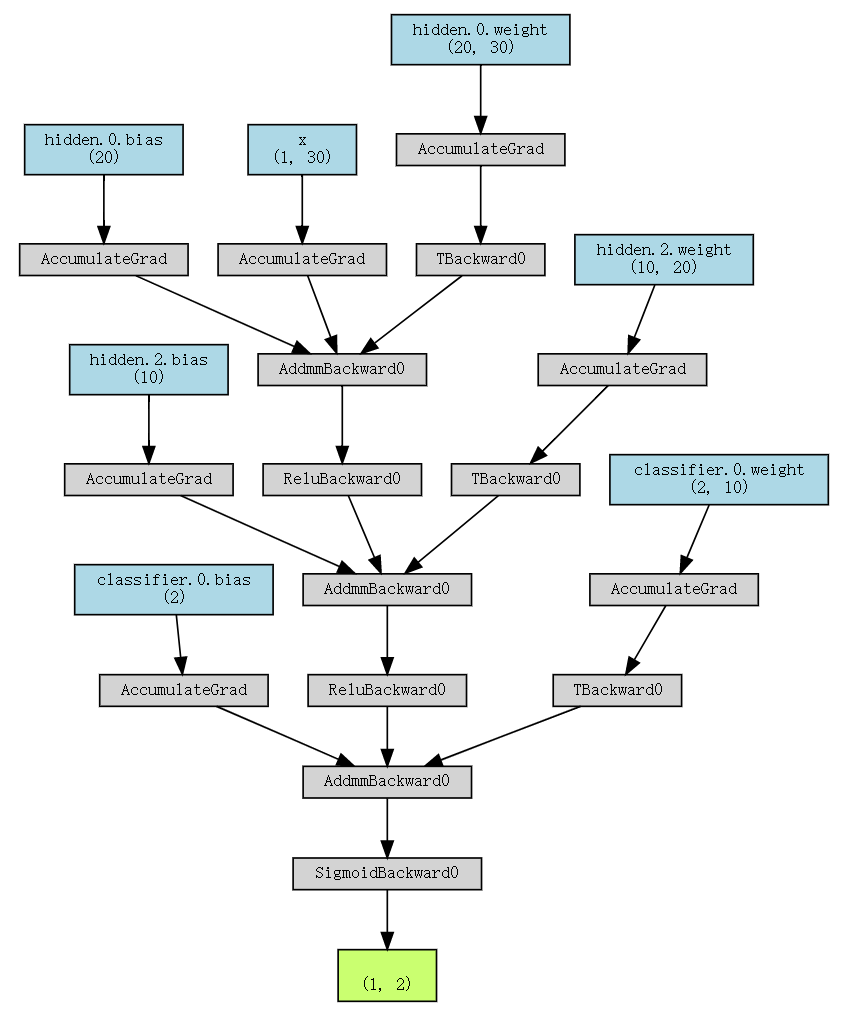
 也可以利用torchviz来实现模型的可视化

from torchviz import make_dot
x=torch.randn(1,30).requires_grad_(True)
y=model(x)
photo=make_dot(y,params=dict(list(model.named_parameters())+[('x',x)]))
photo

 

这个结构图主要体现了输入数据和层权重的计算过程。

1.3.3 训练模型

import hiddenlayer as hl

# 定义优化器
optimizer=torch.optim.Adam(model.parameters(),lr=0.01)
# 定义损失函数
lossfuc=nn.CrossEntropyLoss()

history=hl.History()
canvas=hl.Canvas()

# 训练过程可视化
for epoc in range(20):#训练轮次
    for step,(b_x,b_y) in enumerate(train_loader):#遍历生成器
        output=model(b_x)
        train_loss=lossfuc(output,b_y)
        optimizer.zero_grad()
        train_loss.backward()
        optimizer.step()
        
    #输出每轮的结果
    output=model(x_test)
    # 取值较大的为最终预测结果
    _,prelab=torch.max(output,1)
    # 计算该轮测试精度
    test_accuracy=accuracy_score(y_test,prelab)
    history.log(epoc,train_loss=train_loss,test_accuracy=test_accuracy)
    # 绘图
    with canvas:
        canvas.draw_plot(history['test_accuracy'])
        canvas.draw_plot(history['train_loss'])

 可以看到有训练集损失不断下降，而测试集精度上升到一定程度后便不再上升，这和之前的经验相符。

不知道为什么，重复运行这段代码，模型将会在原来基础上继续训练，而非重新开始，可能是代码哪里保存了模型的权重，暂时不知道具体原因

1.4 小结

这一章节给出了一些经典的问题，数据处理的简单办法，以及全连接神经网络的构建、编译和训练。对我而言最大的感受就是具体问题所面临的困难是很不相同的。到目前还没有对模型进行直接的改进，因此算是对神经网络有了一个大概的轮廓。

---

编辑到两万字以上就开始变得很卡，编辑起来很难受，不得已只能在这里中断。。