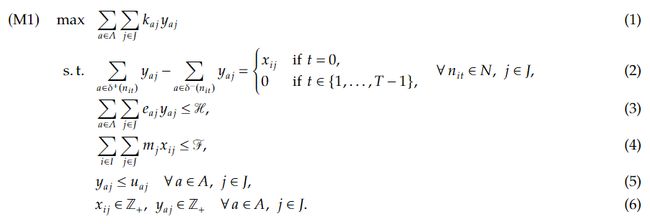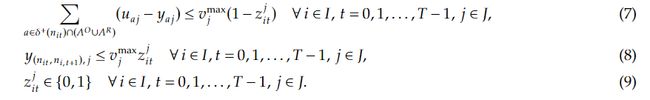交通 | 二氧化碳排放约束的混合共享汽车选址与重定位问题
编者按
本文考虑了混合车辆的共享汽车选址以及重定位问题,建立了包含单程式旅行需求以及往返式旅行需求的整数线性规划模型。采用了波士顿Zipcar公司2014年的数据进行验证,发现模型可以提高汽车利用率和顾客服务率。
1.引言
目前,共享汽车公司越来越支持采用电动汽车,在满足多样化顾客需求的同时尽可能减少二氧化碳排放。本文考虑了混合车辆的共享汽车选址以及重定位问题,建立了包含单程式旅行需求以及往返式旅行需求的整数线性规划模型。为了模拟车辆的移动,本文在基于确定性时变需求的时空网络上采用了最小化成本模型。模型的目标是最大化净收益,即租车收益减去系统运营成本,约束包括车辆预算约束以及二氧化碳排放约束。另外,本文采用了先到先服务的原则以减少出行需求的延误。
根据2014年波士顿Zipcar的共享汽车数据进行数值实验,本文对站点选址、车型选择以及系统对环境的影响进行了优化。结果显示,模型得到决策提高了汽车利用率以及顾客的服务率。尽管二氧化碳排放限制降低了共享汽车系统的收益,但顾客对能源高效车辆的高需求可以弥补损失。
2.模型描述
2.1时空网络公式
将一个大的都市划分为多个小的区域,并用 I I I表示所有区域的集合。每个区域都有一个停车的站点以满足不同时段到达该区域的车辆需求。给定需求数据,我们表征了原点和目标区域之间的旅行,并用 O ∈ { 0 , 1 , . . . , T } O\in \{0,1,...,T\} O∈{0,1,...,T}和 D ∈ { 0 , 1 , . . . , T } D\in\{0,1,...,T\} D∈{0,1,...,T}表示起点与终点的时段区别。用 J J J表示车辆类型集合,不同车辆的购买成本、需求比例、枚公里收入、维护成本以及二氧化碳排放量不同。令 d i i ′ j t s d_{ii'jts} dii′jts和 r i i ′ j t s r_{ii'jts} rii′jts表示j类型的车辆在t时段i区域被租用并于s时段i‘区域被归还情况下的需求量以及单位收益。令 c j c_j cj表示j类型车辆的单位时段的二氧化碳排放量, b j t b_{jt} bjt和 p j t p_{jt} pjt表示j车辆的维护成本以及单位时段的闲置成本, l i i ′ l_{ii'} lii′表示i区域与i’区域之间的最小旅行时间, c r e l c^{rel} crel表示单位时段的重定位成本。
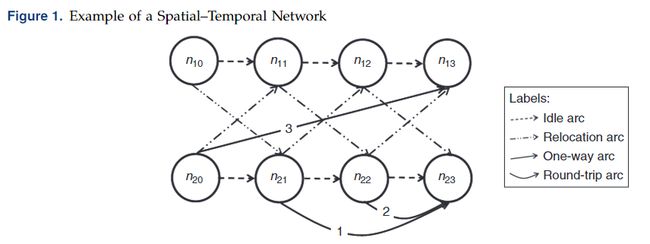
我们构建一个时空静态网络 G ( N , ) G(N,) G(N,),每个节点 n i t ∈ N n_{it}\in N nit∈N代表周期 t ∈ { 0 , 1 , . . . , T } t\in \{0,1,...,T\} t∈{0,1,...,T}的区域i∈I。该网络中的弧d 指向,代表了从一个区域到另一个区域的车辆时空移动。特别的,我们创建了四种类型的弧:空闲弧,单向弧,往返弧和重定位弧。闲置弧, a = ( n i , t , n i , t + 1 ) ∈ A I a=(n_{i,t},n_{i,t+1})\in A^I a=(ni,t,ni,t+1)∈AI,表示从周期t到周期t +1的同一区域I区域的汽车流动;单向弧, a = ( n i , t , n j , s ) ∈ A O a=(n_{i,t},n_{j,s})\in A^O a=(ni,t,nj,s)∈AO和往返弧, a = ( n i , t , n j , s ) ∈ A R a=(n_{i,t},n_{j,s})\in A^R a=(ni,t,nj,s)∈AR,表示在周期T中从区域i行驶并到达S时期的J区的顾客需求流(前者为单程式需求,后者为往返式需求);重定位弧 a = ( n i , t , n i ′ , t + l i i ′ ) ∈ A R E L a=(n_{i,t},n_{i',t+l_{ii'}})\in A^{REL} a=(ni,t,ni′,t+lii′)∈AREL,表示在周期时,将重新定位的汽车流从周期t的i区域携带到t+lii’时期区域i’。
图1显示了一个时空网络的示例,该网络为此有两个区域{1,2}和四个周期{0,1,2,3}。每个节点 n i t n_{it} nit代表周期t的区域i。我们使用不同的箭头来表示图1中四种弧线。两辆车在往返弧 ( n 22 , n 23 ) (n_{22},n_{23}) (n22,n23)上移动,意味着这两辆车在时段2离开区域2,并在时段3被还回区域2。三辆车在单向弧线 ( n 20 , n 13 ) (n_{20},n_{13}) (n20,n13)上行驶,这意味着这三辆车在周期为0时离开2区,并在周期3时返回1区。该时空网络流模型使我们能够在每个区域之间跟踪每个区域中汽车的状态(无论是使用还是空闲)。
2.2数学模型
定义整数变量 x i j x_{ij} xij表示每天初始安置在区域i中的j类型车辆数目,整数变量 y a j y_{aj} yaj表示在不同弧 a a a上移动的j类型的车辆数,建立整数线性规划模型如下:
目标函数(1)最大化共享汽车系统运营净收益。流量平衡约束(2)确保每个节点离开的每种汽车数等于其到达的汽车数。约束(3)限制了在T个时间跨度上产生的二氧化碳排放量。约束(4)反映了购买汽车的总预算限制。约束(5)确保每个弧线上的流量不会超过相应的弧能力(即单向和往返弧的需求值)
2.3模型扩展
我们的研究可以从以下几个方面展开。首先,我们可以修改区域i中每个周期t的空闲弧线 ( n i t , n i , t + 1 ) (n_{it},n_{i,t+1}) (nit,ni,t+1)的容量,让它们为区域i中预留的停车位数量。这样的停车位可用性可以作为输入参数,或者我们可以将每个区域中预留的停车位数量定义为整数变量,加上当前变量x和y。这两种修改都没有改变整数规划模型的复杂性。
其次,我们的模型可以通过向(M1)添加约束来处理汽车共享系统的先到先得(FCFS)原则。FCFS是一种服务策略,按照汽车共享请求到达的顺序提供服务。在我们的问题中,FCFS原则要求空闲弧 ( n i t , n i , t + 1 ) (n_{it},n_{i,t+1}) (nit,ni,t+1)具有正向流。为了建模这一规则,我们引入新的二进制变量:
我们将以下约束加入到模型(M1)中确保FCFS原则的实施:
如果j类型车辆在节点闲置,则约束(8)保证 z i t j = 1 z_{it}^j=1 zitj=1,并使得约束(7)的右侧为0,这暗示了所有的顾客需求均被服务。如果有任意顾客需求未被满足,则说明单程式或者往返式顾客需求未到达相应弧的承载上限,约束(7)暗示 z i t j = 0 z_{it}^j=0 zitj=0,约束(8)保证区域i中没有车辆被闲置。
3.数值实验
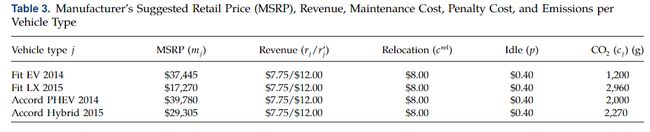
自2000年来波士顿市与Zipcar公司进行着共享汽车合作计划,本文采用了2017年8月15日收集的顾客需求以及运营数据为数值实验构造算例。Figure2显示了不同时段单程式以及往返式需求波动情况,Figure3显示了波士顿市的区域划分情况,Table3为不同车辆类型的相关参数情况。
3.1单程式需求比例对系统影响
下图为M1模型以及M2模型中单程式需求比例增加对系统运营的影响。随着单向旅行的比例增加,两个模型的最佳目标值增加(单程式需求从0%到100%增加时,系统最优收益增加约为30%)。我们注意到(M1)和(M2)的最佳目标值非常相似,但是CPU时间从(M1)到(M2)显着增加。这是因为(M2)包括其他“大M”约束(7) - (9),这些约束被认为是解决整数程序的效率低下。因此,我们建议将(M1)用于汽车共享从业者,以在计算效率和模型复杂性之间取得更好的权衡。
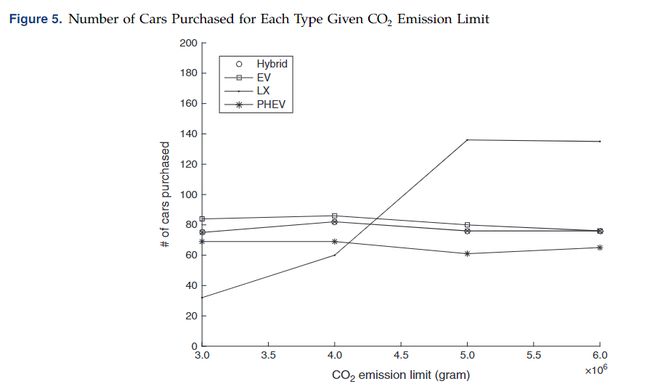
3.2二氧化碳限制的影响
随着二氧化碳排放限量的限制降低,购买的LX数量会增加。我们还注意到,该模型显示出对混合动力汽车的明显偏好,而混合动力汽车始终比PHEV购买更多。这可能归因于PHEV的高成本,尽管PHEV和混合动力车在技术和功能上相似。该模型可以用于共享汽车服务公司,以确定购买最优数目的各类型车辆进行服务。使用此模型的车队组成分析可以在环境保护的基础上区分更有利可图的汽车模型。
4.总结与展望
未来有希望的研究方向是共享自动驾驶车辆的车队分布。将自动驾驶汽车引入道路交通可以通过多种形式,这对未来共享汽车的普及与应用尤为关键。正如共享汽车领域引入电动汽车一样,对自动驾驶的引入也是一个自然的步骤。
参考文献:
[1]Joy Chang;Miao Yu;Siqian Shen;Ming Xu.Location design and relocation of a mixed car-sharing fleet with a CO2 emission constraint(Article)[J].Service Science,2017,Vol.9(3): 205-218