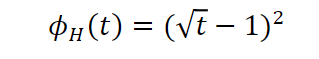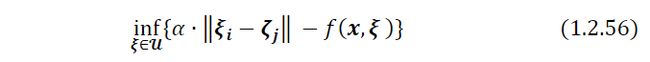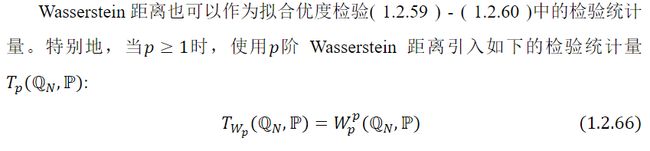OR青年 | 分布鲁棒优化研究报告

作者信息：
胡海涛，东北财经大学，管理科学与工程学院，管理科学与工程在读博士

编者按：

本文系『OR青年计划』成果，是胡同学在孙秋壮老师指导下完成。由『运筹OR帷幄』社区主办的『OR青年计划』，旨在帮助对运筹学应用有理想和追求的同学，近距离与学界、业界导师交流课题，深入了解运筹学的细分方向，为后续的深造、就业生涯打下坚实的基础。关于第二届『OR青年计划』的详细情况，请参考成果汇报来啦！第二届OR青年计划之学界实验室结营直播预告！！！

1.引言

1.1导论

考虑经典的鲁棒优化，传统的最小最大鲁棒优化模型：

随机优化是不确定性决策的另一个主要建模框架，它提供了一种不同的方法。随机规划不是基于确定性的不确定集合和最坏情况，而是基于完全已知的概率分布和平均性能准则：

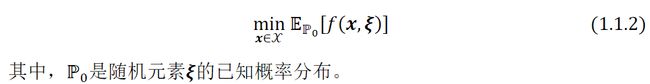
从上述模型可以看出，鲁棒优化和随机规划几乎是两种方向相反的方法，即鲁棒优化完全摆脱任何概率分布而随机优化完全包含于一个固定的概率分布。

尽管上述两种方法取得了一定程度上的成功，但这两种方法也受到其建模前提的限制，具体如下：首先，如果鲁棒优化忽略了有价值的概率信息，那么可能导致过于保守的计算结果，而随机规划可能需要过多的概率分布信息，但是这些信息对于建模者来说可能是不可用的；其次，从鲁棒或随机规划模型得到的解可能在样本外测试中表现很差，或者可能存在无法通过简单地增加采样数据的规模来消除的内在偏差；第三，鲁棒模型可能在计算上很难求解，特别对于自适应鲁棒优化问题(Adaptive Robust Optimization)，而随机规划往往会涉及高维积分，同样在计算上难以求解。

为了解决上述局限性，对鲁棒优化和随机规划进行推广，具体思路如下：相比于假设一个特定的概率分布，现在考虑有一定数量的模糊的概率分布。例如，不考虑假设随机元素的概率分布是均值为0，方差为1 的标准高斯分布，而是可以考虑均值相同但方差不同的所有高斯分布，或者可以考虑均值接近于0，方差接近于1 的所有分布。这种关于概率分布的模糊性可以通过指定一个集合来构建，其元素是可能考虑到的所有概率分布，称这个集合为模糊集。(Ambiguity set)
按照上述对模糊集的定义，上文的随机规划模型(1.1.2)可以被视为具有一个只有一个元素的模糊集合，即 = {名义分布ℙ0 }。一旦至少有一个元素，(1.1.2)模型就需要考虑最小化平均成本，此时，考虑最坏情况下的鲁棒优化方法得以运用，以最小化模糊度集合中所有需要考虑的全部分布的最坏情况为平均代价。因此，得出以下分布鲁棒优化模型(Distributionally Robust Optimization，DRO):

注意，如果模糊集只包含一个分布，那么DRO 模型(1.1.3)就退化为随机规划模型(1.1.2)。相反，如果包含固定支撑集上的所有分布，则DRO 模型(1.1.3)退化为一个鲁棒优化模型(1.1.1)，其中为不确定集。因此，DRO 提供了一个统一的框架，其中鲁棒优化和随机优化是两种特殊情况。

1.2 典型的静态分布鲁棒优化

分布鲁棒优化模型大致分为两类：基于矩信息(矩模糊集)的DRO 和基于距离信息(距离模糊集)的 DRO。基于矩的模糊集是利用基本分布的矩信息来定义的，例如均值和协方差，而基于距离的模糊集是通过标称分布之间的某种“距离”来定义的，这种距离通常是通过数据驱动的方法(如采样)和其他邻近概率分布来获得的。有时，所使用的距离并不是真实距离，即不是概率分布空间中的度量。尽管如此，还是捕捉到了分布之间的某种差异。

1.2.1 广义矩信息模糊集

（1）模型重构

在实际应用中，往往不知道潜在的随机元素的真实分布，而只知道其部分矩的信息，如均值、方差或协方差。例如，在数据驱动的建模框架中，可以从未知分布中提取独立同分布(iid)样本，从而估计相关的矩信息。均值和方差提供了随机变量的一些基本特性。根据数学中的经典问题矩问题，来对概率分布进行确定。常见的基于矩信息的模糊集如下：

具有此模糊集合的 DRO 问题( 1.1.3 )在最坏情况概率分布上(the worst-case probability distribution)有如下的内部最大化问题:

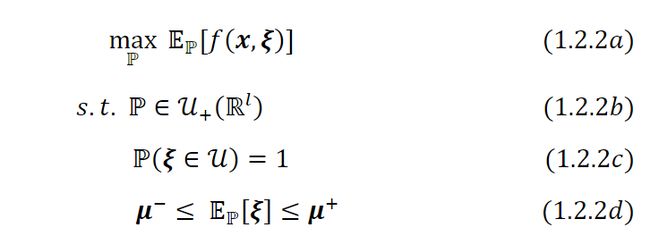
这个内部最大化问题( 1.2.2 )一般是一个具有无穷多个变量和有限个约束的优化问题。

在处理无穷维问题( 1.2.2 )之前，先考虑一个重要的特例，其模糊度集合中的概率分布是固定在有限支撑集上的离散分布。例如，分布的支撑是具有个固定场景的集合 ={,,…,}。上的任意概率测度都可以用一个向量={1,2,…,} ∈ℝ表示。在这种情况下，问题( 1.2.2 )具有以下形式:

这是一个有限维优化问题。值得注意的是，目标函数是中的线性函数，因为期望运算${\mathbb{E}}_P$是概率测度ℙ的线性函数，所以( 1.2.3 )是关于ℙ的一个线性规划问题。现在考虑一般概率分布下的内部最大化问题：

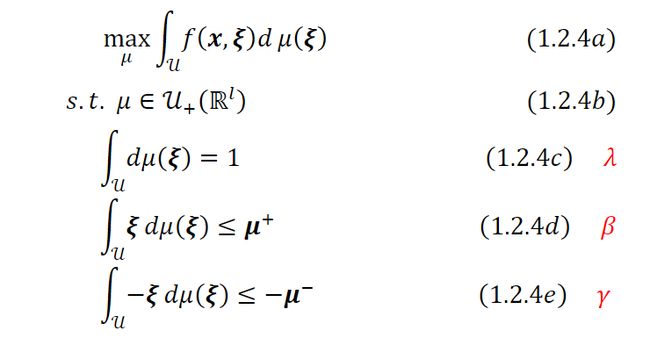
关于的线性积分意味着( 1.2.4 )是无穷维空间中的一个线性规划问题。现在考虑( 1.2.4 )的对偶问题。为得到对偶有限维优化问题，构造拉格朗日函数：

假设内部最大化问题( 1.2.2 )与其对偶问题( 1.2.6c ) - ( 1.2.6d )之间存在强对偶关系，可以在DRO 问题( 1.1.3 )中用其对偶问题代替内部最大化问题。然后，得到如下静态鲁棒优化问题:

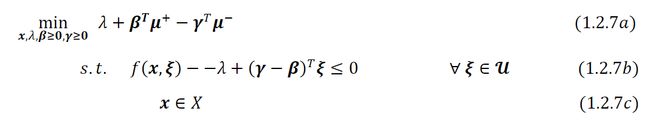
上述过程表明，将 DRO 问题通过对偶化重新表述，可以转化为经典鲁棒优化问题。关于( 1.2.2 )与其对偶( 1.2.6c ) - ( 1.2.6d )之间强对偶性的充分条件，可参考文献[2,3,4]

(2)基于交叉二阶矩信息的模糊集

现在考虑如何将交叉二阶矩信息合并到一个模糊集，以及如何重新表述产生的DRO。

这个模糊集合，也称为切比雪夫模糊集合[5~8]，包含所有具有相同均值0的概率测度。第三个约束是半正定约束，指ℙ的协方差矩阵应该接近已知的协方差矩阵0，而是控制模糊度集大小的缩放参数。直接考虑连续分布的情形，并给出如下最大化问题的对偶:

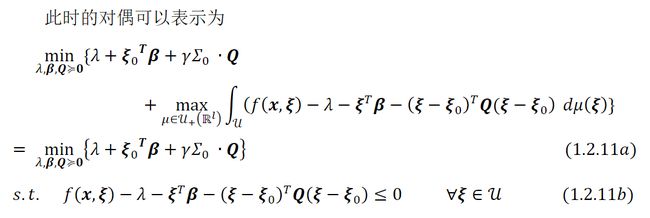
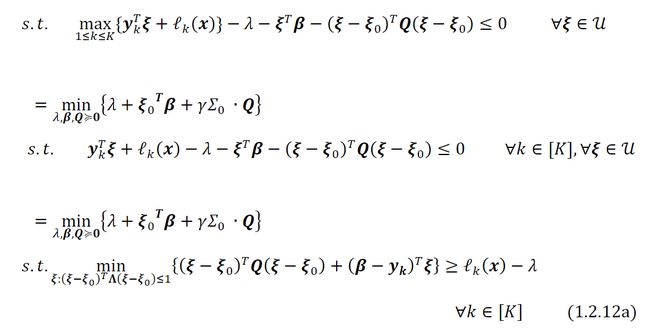
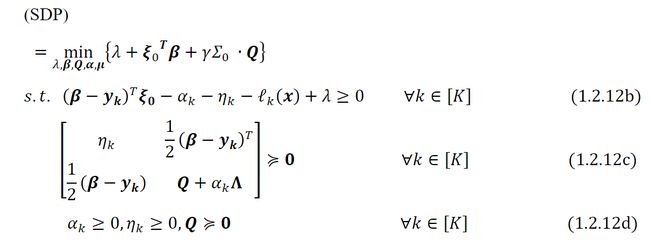
1.2.2 散度模糊集合重构

考虑到基于矩的模糊集是包含具有一些共同矩信息的的概率分布，这种类型的模糊集缺乏具有代表性的特定分布。例如，在单纯使用矩模糊集中，没有一个简单的方法去定义名义分布或经验分布。然而，通常情况下，建模者可以通过从真实分布中抽样，来获取一些经验分布。因此，研究一个与这个特定的经验分布比较接近的分布的模糊集就具有一定的意义，并期望选择合适的模糊集，来在统计意义上包含真实的、未知的分布。这正是研究基于距离的模糊集的意义。基于距离的模糊集的关键问题是如何度量概率分布之间的接近程度。测量概率分布之间的距离是统计学中的一个经典问题，为此提出了许多方法，如散度方法。

（1）Kullback-Leibler(KL)散度

Kullback-Leibler(KL)散度是研究散度的最著名的例子。为了介绍KL 散度，首先定义如下函数():ℝ+ →ℝ ：

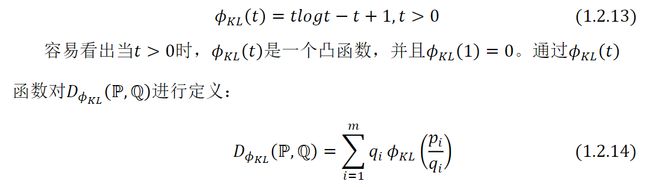
其中，ℙ和ℚ两个离散的概率分布被定义在相同确定支撑集，={,,⋯,}⊆ℝ 有 个 场 景 ，并 且 ℙ 和ℚ 用 两 个 向量 表示 ， ℙ={1,2,…,} , ℚ={1,2,…,} ，向量元素为对应场景发生的概率。(ℙ,ℚ)称为ℙ关于ℚ的KL 散度，将( 1.2.13 )代入( 1.2.14 )：

KL 散度与 Shannon’s 熵函数(ℙ)=−ℙ[log (ℙ())]和交叉熵函数H(ℙ,ℚ) = −ℙ[log (ℚ())]密切相关。容易看出(ℙ,ℚ)=H(ℙ,ℚ)−(ℙ)。交叉熵H(ℙ,ℚ)可以看作是从ℙ到ℚ的距离的度量。然而，它的缺点是H(ℙ,ℙ) = (ℙ)≠0 。因此，考虑从(ℙ,ℚ)中减去(ℙ)来定义KL 散度。在信息论中，KL散度(ℙ|ℚ)也称为ℙ关于ℚ的相对熵。因此为了有一个确定的KL 散度，对于所有的 ∈[ ]，当 =0时，需要有 =0。

如果对于某个 ∈[ ]:= { 1,2,…, }， =0但 >0，则 KL 散度有项 log(/0)=∞。如果 =0且 =0，则定义0log(0/0)=0。当ℙ和ℚ满足这个性质时，称ℙ关于ℚ是绝对连续的，也称为ℙ由ℚ控制。在这种情况下，对于所有的情形，/的比值是确定的，其中 ≠0。这个比率被称为ℙ ℚ的密度。KL 散度具有以下基本性质：

（2）散度一般定义

满足上述条件的任何函数都得到散度。下表列出了一些广泛使用的 -散度的例子。

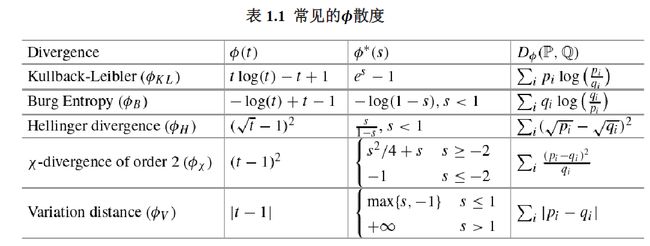
（3）基于散度一般形式的模糊集DRO 等价转换

考虑使用散度来构建模糊集：设ℚ0是决策问题中潜在随机参数真实概率分布的一个估计，使用散度来定义下面的模糊集：

假设离散概率测度ℙ在有限支撑上具有个元素的，为控制模糊集大小的正参数。散度和的选择取决于建模者，反映了建模者的风险厌恶偏好。现在考虑将基于上述模糊集的 DRO 问题进行重构，关键问题在于对标准 DRO 问题( 1.1.3 )中的内部极大化问题处理，具体如下：

构造(1.2.20)的拉格朗日函数

注意，内部最大化问题在上是完全可分的。因此，只需要单独查看每个上的最大化问题。令ℎ ={(,)−}，则每个的子问题为：




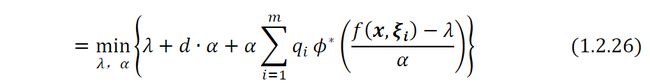
由于是一个凸函数，如果满足原问题的Slater 条件，则原问题( 1.2.20 )和对偶问题( 1.2.26 )之间具有强对偶性，因为可以选择ℙ =ℚ0，并且假设每一个都是正的。

此外，如果对于每个，(,)是关于的凸函数，则式( 1.2.28 )是一个凸优化问题：对于任意非负的，共轭函数()∗始终是一个闭凸函数，因为它是( ,)中线性函数的逐点最大值，如式( 1.2.25 )所示。因此，很容易证明当 ≥0时，复合函数()∗((,)− ) 是关于( , ,)的凸函数。因此，( 1.2.28 )是关于( , ,)凸优化问题。

（4）等价转换的其他例子

1.KL散度

2.Hellinger 散度

目标中的求和函数可以进一步重新表述为 SOC 约束：通过引入一个辅助变量，对每个 ∈[]:

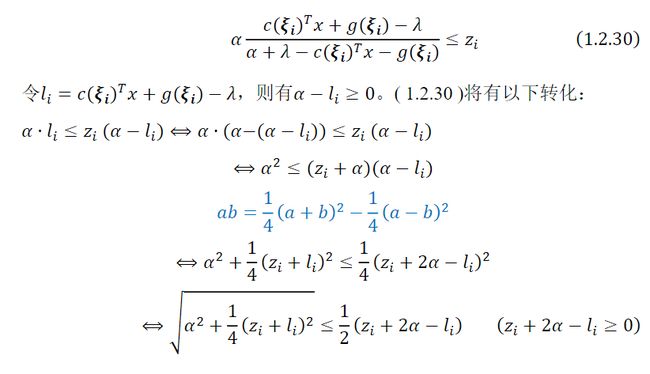
3.Variation distance

通过推导发现，即使DRO 的目标函数(, )是关于x 的非线性凸函数，上述重构仍然是凸的。

1.2.3基于沃瑟斯坦距离的模糊集的重构

（1）最优运输问题与Wasserstein 距离

假设有个供应商和个客户，供应商有单位的商品供应量，消费者有单位的商品需求量。对于每一对 ∈[] = { 1，…， }， ∈[ ] = { 1，…， }，从供应商运输一单位货物到消费者需要花费。目标是找到一个运输计划，以最小的运输成本从供应商处发送所有的商品，来满足客户的所有需求。这个问题被称为最优运输问题。令表示从供应商发送到消费者的商品数量。然后，最优运输问题可以表示为如下的线性规划：

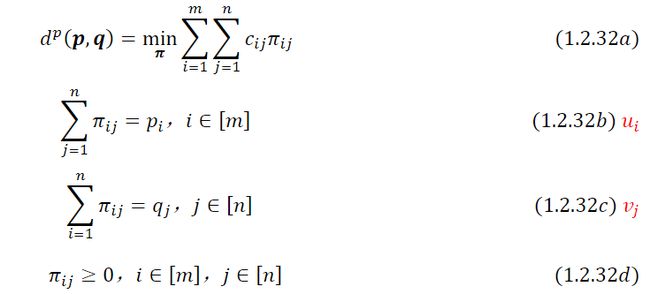
现在假设最优运输问题中的供给和需求是概率测度，在样本空间Ω⊆ℝ 上，供给=(1,2,⋯,)是Ω中个支撑点{，，⋯，}上的概率质量函数，需求=(1,2,⋯,)是Ω中个支撑点{，，⋯，}上的另一个概率质量函数。根据运输问题的约束，∑ ∑ ∈[]∈[] =1， ≥0， 是{，，⋯，} ×{，，⋯，}上的联合概率分布。那么运输问题的约束可以解释为的边际分布是和。单位运输成本取决于和两点之间的距离，可以用两个向量和之间的距离来刻画， =‖ −‖。那么原始最优运输问题可以看成是寻找一个联合概率分布 ，其边缘分布为和 ，使得在{，，⋯，}上支持的概率测度可以通过以最经济有效的方式运输到在{，，⋯，}上支持的概率测度 。

Wasserstein 距离可以定义为ℙ()中ℙ和ℚ的一般概率测度，而不一定是有限支撑上的离散分布，其中是ℝ的一个闭子集，定义ℙ和ℚ之间的阶Wasserstein距离为:

（2）Wasserstein 距离与散度的比较

通过将Wasserstein 距离和散度对比，发现散度有两种Wasserstein 距离没有的不足。Wasserstein 距离的优点来自于它是概率测度上的一个真正的距离函数，即一个度量，而散度不是。

1.在散度模糊度集合(ℚ0,)中，若名义分布ℚ0是具有有限支撑的离散测度，则模糊度集合(ℚ0,))中的任意概率测度ℙ均满足

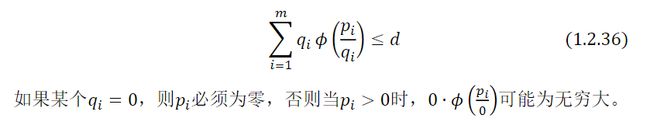
例如，除了变化距离外，表1.1 中所有其他的散度对 > 0都有0∙ (/0)=∞。因此，在这样一个散度模糊集合中的所有分布都必须是关于ℚ0绝对连续的，基于沃瑟斯坦距离的模糊度集不存在这个问题。即使当ℚ0是离散分布时，沃瑟斯坦球仍然可以包含连续分布。

2.由于散度一般不是一个距离函数，例如，只有表1.1 中的变化距离是一个真实的距离，散度模糊度集可能有一些违反直觉的行为。

（3）等价转换

目标是通过凸优化对偶理论，找到一个等价的重新制定的内部最大化问题。首先研究最简单的情形，假设ℙ和ℚ0都被限制为有限支撑上的离散分布，即

其中 是Dirac 测度，在处为1，其他处为0。在这种情况下，Wasserstein 距离由线性规划( 1.2.32 ) - ( 1.2.33 )给出。下面给出DRP问题( 1.2.38 )的内部最大化的重新表述。

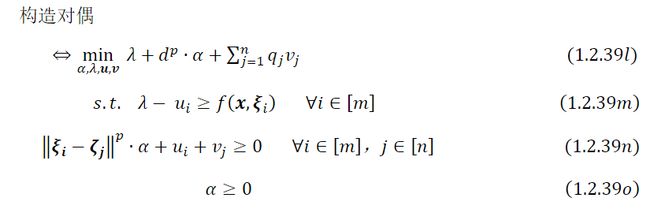
(1.2.39d) 由于在推导过程中所有的程序都是线性的，所以只要初值问题( 1.2.39a ) - ( 1.2.39b )是可行的，强对偶性始终成立。对( 1.2.39a ) - ( 1.2.39b )进行重新构造还有一种等价的方法，更容易推广到连续概率分布的无穷维情形，对所涉及的所有线性程序假设强对偶成立：

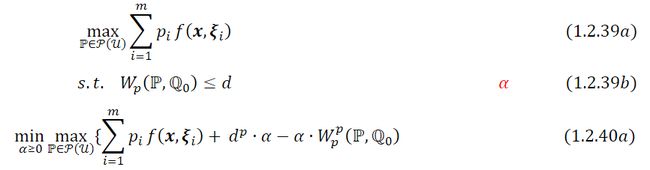
在( 1.2.40a )中松弛了Wasserstein 距离约束，形成了拉格朗日对偶。在最后一步( 1.2.40b )中，对于所有 ∈[]，使用约束$p_i={\sum }_{j=1}^n{\pi }_{ij}$$消除了ℙ变量。现在对 ( 1.2.40b )中内部极小化问题进一步简化：

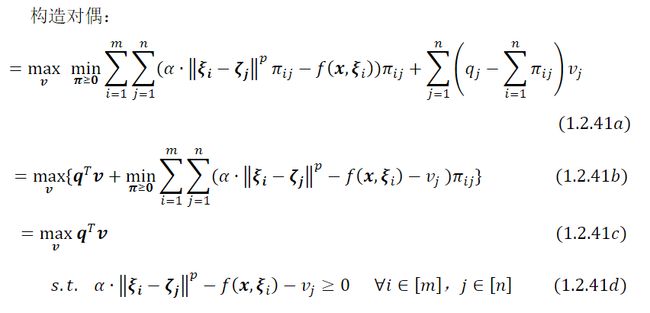
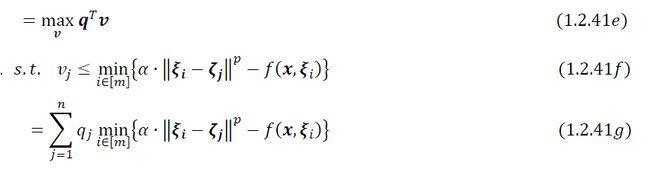
更一般的情况是当ℙ和$Q_0$均为连续分布时,ℙ和$Q_0$的支撑空间也可以从有限维欧几里得空间ℝ推广到一个非常一般的拓扑空间，称为波兰空间。在Wasserstein 距离的定义中使用的范数被波兰空间的度量所取代，对偶的形式与上述两种特殊情况完全相同。

（4）对有限凸规划的进一步重新构造

根据上文的等价推导的结果，由于( 1.2.43b )和( 1.2.44b )都涉及相当复杂的嵌套优化问题，因此需要进一步整合成现有的求解器可以直接求解的形式，重点讨论$Q_0$是具有有限支撑的离散测度的情形，并 假设Wasserstein 距离的阶数为1，即 = 1。

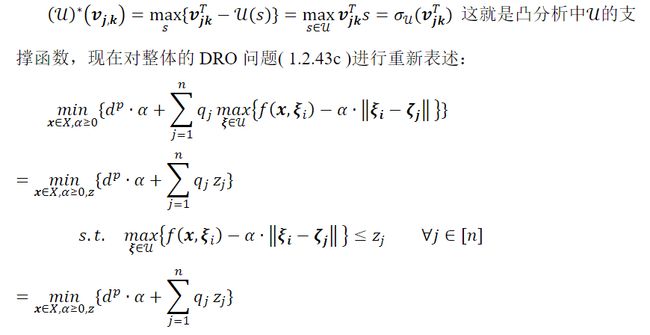
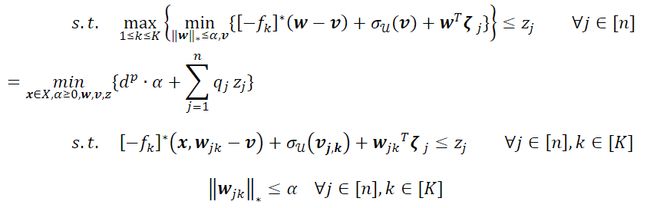
如果[−]∗，，和‖∙‖∗可以用凸锥约束表示，那么上面的改写给出了一个凸锥优化问题，可以通过可用的求解器求解。

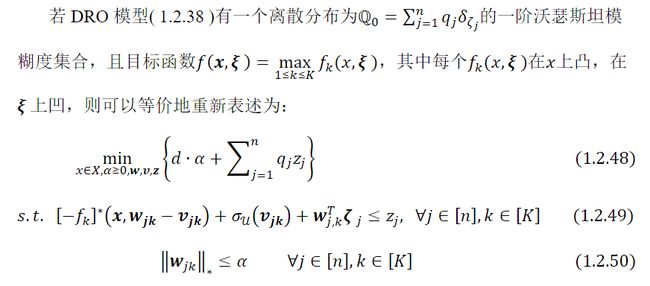
（5）最坏情况分布和与鲁棒优化的关系

现在考虑( 1.2.44a )中的最坏情况分布ℙ：原问题( 1.2.44a )存在最坏情况分布ℙ当且仅当对偶问题( 1.2.44b )取得有限最小值。当最坏情况分布存在时，以扰动$Q_0$的形式出现。可以从( 1.2.44b )中看到，对于每个，内部极小化问题将某个 ( ) 确定为它的极小点。这是一个从到 ( ) 的映射。这样的映射将概率密度从$Q_0$转移到ℙ。由于每个可能导致内部极小化问题的多个极小点，因此可能存在多个这样的映射。事实证明，对于( 1.2.44a )，最坏情况分布ℙ*可以构造为由两个这样的映射形成的两个转移概率分布的凸组合。例如，考虑ℚ0为离散分布的情形，

假设内部最小化问题:

这种对( 1.2.43a )中最坏情况分布的刻画将DRO 问题( 1.2.38 )重新表述为一个经典的鲁棒优化问题。特别地，将( 1.2.43a )构造为如下鲁棒优化问题

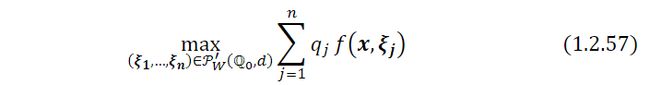
鲁棒优化问题考虑最坏情况下分布的情况以期望最大化成本，( 1.2.43a ) - ( 1.2.58 )反应了分布鲁棒优化和经典鲁棒优化之间的关系，即鲁棒优化问题可以为DRO 问题提供一个近似。

1.2.4 确定模糊集合大小的统计方法

为了给上述构造模糊集提供严格方法论，引入统计学的观点，假设拥有的数据是从一个未知分布ℚ抽取的iid 随机样本。为了得到ℚ的具体分布，或者找到一组与ℚ近似的分布，基于假设检验或拟合优度检验分方法，在给定一个概率分布ℙ和一组从ℚ中抽取的个iid 数据{̂,,̂⋯,̂}，检验以下原假设：

(1)基于散度的模糊集

（2）基于沃瑟斯坦的模糊集

总之，统计假设检验( 1.2.59 ) - ( 1.2.61 )提供了一种激发和构造模糊集的主要方法，还为标准鲁棒优化问题构造数据驱动的不确定集。参考[19]对多种不确定性集合的统一阐述和构造，参考[ 20 ]中使用线性回归和t 检验来校准投资组合优化中的不确定性集，以及[ 21 ]中使用′2检验来构造库存问题中的模糊集合。

参考文献：

1. Lin,G.D.(2017).Recent developments on the moment problem. Journal of Statistical Distributions and Applications,4,5. https://doi.org/10.1186/s40488-017-0059-2.
2. Shapiro, A.(2001).On Duality theory of conic linear problems. In M. A. Goberna & M. A . Lopez(Eds.)Semi-Infinite Programming. Nonconvex Optimization and Its Applications(vol.57). Boston, MA: Springer.
3. Ekeland,I.,&Temam,R.(1976).Convex analysis and variational problems. Amsterdam: North-Holland Publishing Company.
4. Schaefer,H.(1971).Topological vector spaces. Berlin: Springer.
5. Zymler,S.,Kuhn,D.,&Rustem,B.(2013).Distributionally robust joint chance constraints with second-order moment information. Mathematical Programming, Series A,137,167–198.
6. Delage,E.,&Ye,Y.(2010).Distributionally robust optimization under moment uncertainty with application to data-driven problems. Operations Research,58(3),595–612.
7. El Ghaoui,L.,Oks,M.,& Oustry,F.(2003).Worst-case value-at-risk and robust portfolio optimization: A conic programming approach. Operations Research,51(4),543–556.
8. Wiesemann,W.,Kuhn,D.,&Sim,S.(2014).Distributionally robust convex optimization. Operations Research,62(6),1358–1376.
9. Kullback,S.,&Leibler,R.A.(1951).On information and sufficiency. The Annals of Mathematical Statistics,22(1),79–86.
10. Jiang,R.,&Guan,Y.(2016).Data-driven chance constrained stochastic program. Mathematical Programming, Series A,158,291–327.
11. Ben-Tal, A.,den Hertog,D.,De Waegenaere, A., Melenberg, B., & Rennen,G. (2013).Robust solutions of optimization problems affected by uncertain probabilities. Management Science,59(2),341–357.
12. Villani,C.(2009).Optimal transport, old and new. Grundlehren der mathematischen Wissenschaften Series(vol.338).Berlin: Springer.
13. Gao, R.,&Kleywegt, A.Distributionally robust stochastic optimization with Wasserstein distance. https://arxiv.org/abs/1604.02199.204 4 Distributionally Robust Optimization.
14. Blanchet, J.,&Murthy, K.(2019).Quantifying distributional model risk via optimal transport. Mathematics of Operations Research,44(2),565–600.
15. Lehmann,E.L.,&Romano,J.P.(2005).Testing statistical hypotheses. Springer Texts in Statistics.
16. Pardo,L.(2020).Statistical inference based on divergence measures. Boca Raton: Chapman & Hall/CRC.
17. Fournier,N.,&Guillin,A.(2015).On the rate of convergence in Wasserstein distance of the empirical measure. Probability Theory and Related Fields,162,707–738.
18. Esfahani,P.M.,&Kuhn,D.(2018).Data-driven distributionally robust optimization using the Wasserstein metric: performance guarantees and tractable reformulations. Mathematical Programming Series A,171,115–166.
19. Bertsimas, B., Gupta, V.,&Kallus, N.(2017).Data-driven robust optimization. Mathematical Programming Series A,167,235–292.
20. Goldfarb,D.,&Iyengar,G.(2003).Robust portfolio selection problems. Mathematics of Operations Research,28(1),1–38.
21. Klabjan,D.,Simchi-Levi,D.,&Song,M.(2013).Robust stochastic lot-sizing by means of histograms. Production and Operations Management,22(3),691–710.