LeetCode每日一题(22年1月17日-1月26日)

1220. 统计元音字母序列的数目

给你一个整数 n，请你帮忙统计一下我们可以按下述规则形成多少个长度为 n 的字符串：
字符串中的每个字符都应当是小写元音字母（‘a’, ‘e’, ‘i’, ‘o’, ‘u’）

• 每个元音 ‘a’ 后面都只能跟着 ‘e’
• 每个元音 ‘e’ 后面只能跟着 ‘a’ 或者是 ‘i’
• 每个元音 ‘i’ 后面 不能 再跟着另一个 ‘i’
• 每个元音 ‘o’ 后面只能跟着 ‘i’ 或者是 ‘u’
• 每个元音 ‘u’ 后面只能跟着 ‘a’

由于答案可能会很大，所以请你返回 模 10⁹ + 7 之后的结果。

解题思路：动态规划，根据规则分析元音 ‘a’ 的前面只能是 ‘e’ 和 ‘i’ 和 ‘u’、元音 ‘e’ 的前面只能是’a’ 和 ‘i’ 、元音 ‘i’ 的后面只能是 ‘e’ 和 ‘o’ 、元音’o’ 的前面只能是 ‘i’、元音 ‘u’ 的前面只能是 ‘i’ 和 ‘o’。
a，e，i，o，u表示k个长度时以对应字母结尾的数量。则有 _a，_e，_i，_o，_u表示 k+1次长度时以对应字母结尾的数量。则有：_a = e+i+u 、_e = a+i、_i = e+o 、_o = i、_u = i+o。
每次计算完毕后都进行对 10⁹+7取模，比最后取模速度快。

public int countVowelPermutation(int n) {
    int m = (int)1e9+7;
    long a,e,i,o,u;
    long _a,_e,_i,_o,_u;
    a = e = i = o = u = 1;
    for(int j = 2;j <= n;j++){
        _a = (e+i+u)%m;
        _e = (a+i)%m;
        _i = (e+o)%m;
        _o = i%m;
        _u = (i+o)%m;
        a = _a;
        e = _e;
        i = _i;
        o = _o;
        u = _u;
    }
    return (int)((a+e+i+o+u) % m);
}

539. 最小时间差

给定一个 24 小时制（小时:分钟 “HH:MM”）的时间列表，找出列表中任意两个时间的最小时间差并以分钟数表示。

示例：

输入：timePoints = ["00:00","23:59","00:00"]
输出：0

提示：

• 2 <= timePoints <= 2 * 10⁴
• timePoints[i] 格式为 “HH:MM”

解题思路：桶排序，一天有1440分钟，将时间用分钟数表示。放入桶中，排序完成后，挨个比较，最后比较最后一个和第一个的时间差。

public int findMinDifference(List<String> timePoints) {
	// 个数大于等于1440，结果一定为0
    if(timePoints.size() >= 1440){
        return 0;
    }
    // 进行桶排序
    boolean[]flag = new boolean[1440];
    for(int i = 0;i<timePoints.size();i++){
        String s = timePoints.get(i);
        String[] strings = s.split(":");
        int index= Integer.valueOf(strings[0]) * 60 + Integer.valueOf(strings[1]);
        if(flag[index] == true){
            return 0;
        }else{
            flag[index] = true;
        }
    }
    // 相邻的时间进行比较
    int min = 1440;
    int i = 0;
    // 找出第一个时间
    while(flag[i] == false){
        i++;
    }
    int pre = i;
    i++;
    // 依次与前一个时间进行比较
    while(i < 1440){
        if(flag[i]){
            min = Math.min(min,i - pre);
            pre = i;
        }
        i++;
    }
    // 找出第一个时间，作为第二天的时间，与前一天最后一个时间进行比较
    int j = 0;
    while(flag[j] == false){
        j++;
    }
    // 返回结果
    return Math.min(min,j + 1440 - pre);
}

219. 存在重复元素 II

给你一个整数数组 nums 和一个整数 k ，判断数组中是否存在两个不同的索引 i 和 j ，满足nums[i] == nums[j] 且 abs(i - j) <= k 。如果存在，返回 true ；否则，返回 false。

示例：

输入：nums = [1,2,3,1], k = 3
输出：true

输入：nums = [1,2,3,1,2,3], k = 2
输出：false

提示：

• 1 <= nums.length <= 10⁵
• -10⁹ <= nums[i] <= 10⁹
• 0 <= k <= 10⁵

解题思路：滑动窗口，窗口大小为k。使用哈希表判断窗口中有没有重复元素。

public boolean containsNearbyDuplicate(int[] nums, int k) {
    HashSet<Integer> set = new HashSet<>();
    int left = 0,right = k;
    // 初始化滑动窗口
    for(int i = 0;i <= k && i < nums.length;i++){
        if(!set.add(nums[i])){
            return true;
        }
    }
    // 窗口前移，判断是否有重复元素
    while(right < nums.length - 1){
        set.remove(nums[left++]);
        if(!set.add(nums[++right])){
            return true;
        }
    }
    return false;
}

2029. 石子游戏 IX

Alice 和 Bob 再次设计了一款新的石子游戏。现有一行 n 个石子，每个石子都有一个关联的数字表示它的价值。给你一个整数数组 stones ，其中 stones[i] 是第 i 个石子的价值。
Alice 和 Bob 轮流进行自己的回合，Alice 先手。每一回合，玩家需要从 stones 中移除任一石子。

如果玩家移除石子后，导致所有已移除石子的价值总和可以被 3 整除，那么该玩家就输掉游戏 。
如果不满足上一条，且移除后没有任何剩余的石子，那么Bob将会直接获胜（即便是在Alice的回合）。
假设两位玩家均采用最佳决策。如果 Alice 获胜，返回 true ；如果 Bob 获胜，返回 false 。

示例：

输入：stones = [5,1,2,4,3]
输出：false
解释：Bob 总会获胜。其中一种可能的游戏进行方式如下：
- 回合 1：Alice 可以移除值为 1 的第 2 个石子。已移除石子值总和为 1 。
- 回合 2：Bob 可以移除值为 3 的第 5 个石子。已移除石子值总和为 = 1 + 3 = 4 。
- 回合 3：Alices 可以移除值为 4 的第 4 个石子。已移除石子值总和为 = 1 + 3 + 4 = 8 。
- 回合 4：Bob 可以移除值为 2 的第 3 个石子。已移除石子值总和为 = 1 + 3 + 4 + 2 = 10.
- 回合 5：Alice 可以移除值为 5 的第 1 个石子。已移除石子值总和为 = 1 + 3 + 4 + 2 + 5 = 15.
Alice 输掉游戏，因为已移除石子值总和（15）可以被 3 整除，Bob 获胜。

解题思路：由于玩家的目标是使得已经被移除的石子的价值总和不是3的倍数，因此我们可以把石子分成三类，它们的价值除以3的余数分别为 0, 1, 2。我们可以直接用 0, 1, 2代表它们的价值，对应的石子数量分别为cnt 0,cnt1,cnt2。
可以发现，移除类型0的石子并不会对总和产生影响，如果cnt0为偶数，则类型0的石子不会对结果产生任何影响。
考虑类型1和类型2的石子。
为了保证移除石子的和不为 3 的倍数，操作顺序只有可能为下面的两种情况：
Alice先拿 1，Bob只能拿1，Alice拿2，Bob拿1…
1121212121⋯
如果要想使得 Alice胜利，只能是 类型2的数量比类型1的数量多，最后Bob只能拿 2
Alice先拿 2，Bob只能拿2，Alice拿1，Bob拿2…
2212121212⋯
如果要想使得 Alice胜利，只能是 类型1的数量比类型2的数量多，最后Bob只能拿 1

综合以上两种情况，Alice要想胜利，只要类型1的数量和类型2的数量都存在，Alice总会先拿数量较少的石子（如果类型1与2数量相等，那么Alice无论先拿那个，都会赢）。

考虑类型0的石子为奇数，也可以看做只要一个类型0的石子。
考虑上面两种中，存在一个0的情况：
Alice先拿 1，Bob只能拿1，Alice拿2，Bob拿1…
1121212121⋯
如果1多于2
最后剩下多个1和一个0，Alice只能拿0，Bob只能拿1，Alice胜利。
如果2多于1
最后剩下多个2和一个0，Bob只能拿0，Alice拿2，Bob胜利。
Alice先拿 2，Bob只能拿2，Alice拿1，Bob拿2…
2212121212⋯
如果1多于2
最后剩下多个1和一个0，Bob只能拿0，Alice只能拿1，Bob胜利。
如果2多于1
最后剩下多个2和一个0，Alice只能拿0，Bob只能拿2，Alice胜利。

综合所有情况，Alice获得胜利的条件为，不存在类型0时，只要类型1的数量和类型2的数量都存在即可，存在类型0时，只有当类型1比类型2的数量大于2的时候或者当类型2比类型1的数量大于2的时候，Alice才能赢（Alice先拿多的）。

public boolean stoneGameIX(int[] stones) {
    int[] cut = new int[3];
    // 统计各个类型的石头数量
    for(int val : stones){
        cut[val%3]++; 
    }
    // 根据石子类型0判断
    if(cut[0] % 2 == 0){
        return cut[1]>=1 && cut[2]>=1;
    }
    // 有一个石子类型0
    return cut[1] - cut[2] >= 2 || cut[2] - cut[1] >= 2;
}

1345. 跳跃游戏 IV

给你一个整数数组 arr ，你一开始在数组的第一个元素处（下标为 0）。
每一步，你可以从下标 i 跳到下标：

• i + 1 满足：i + 1 < arr.length
• i - 1 满足：i - 1 >= 0
• j 满足：arr[i] == arr[j] 且 i != j

请你返回到达数组最后一个元素的下标处所需的 最少操作次数 。
注意：任何时候你都不能跳到数组外面。

输入：arr = [100,-23,-23,404,100,23,23,23,3,404]
输出：3
解释：那你需要跳跃3次，下标依次为 0 --> 4 --> 3 --> 9。下标9为数组的最后一个元素的下标。

提示：

• 1 <= arr.length <= 5 * 10⁴
• -10⁸ <= arr[i] <= 10⁸

解题思路：BFS，把数组看着一个图，数组中值看作图中的一个节点，每一个节点 i 与 i + 1和 i - 1 (i为数组的下标) 相连，还与相同值的元素相连。
示例：
arr = [100,-23,-23,404,100,23,23,23,3,404]
图为：
图为无向图，边的权重为1。

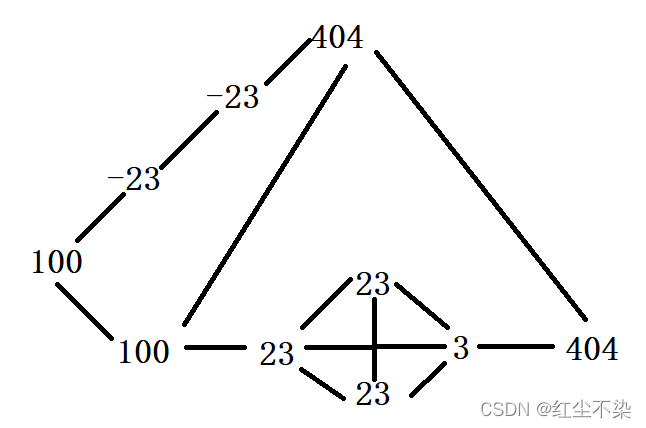
对图做BFS，从根节点开始，依次判断相连的节点是否访问过，未访问过，加入队列，直到访问到arr[arr.lenthg - 1] ，BFS结束。

public int minJumps(int[] arr) {
    // 记录相同值的下标
    HashMap<Integer,List<Integer>> hashMap = new HashMap<>();
    // 队列，做 BFS
    Queue<int[]> queue = new ArrayDeque<>();
    // 记录是否访问过
    boolean[] vis = new boolean[arr.length];
    // 将相同值的元素下标保存到一个数组中
    for(int i = 0; i < arr.length;i++){
        List<Integer> list = hashMap.getOrDefault(arr[i],new ArrayList<>());
        list.add(i);
        hashMap.put(arr[i],list);
    }
    //进行 BFS，数组中下标0表示在arr中下标，第二个0表示步长
    queue.add(new int[]{0,0});
    vis[0] = true;
    int ans = 0;
    int index,step;
    int n = arr.length;
    while(vis[n - 1] == false){
        // index下标，step步数。
        index = queue.peek()[0];
        step = queue.poll()[1] + 1;
        ans = step;
        // 判断 index + 1 是否访问过
        if(index + 1 < n && !vis[index + 1]){
            // 未访问过，加入
            queue.add(new int[]{index+1,step});
            vis[index + 1] = true;
        }
        // 判断 index - 1 是否访问过
        if(index- 1 >= 0 && !vis[index-1]){
            // 未访问过，加入
            queue.add(new int[]{index-1,step});
            vis[index - 1] = true;
        }
        // 判断是否有相同值的元素
        if(hashMap.containsKey(arr[index])){
            // 有相同元素的值
            for(Integer i : hashMap.get(arr[index])) {
                // 加入队列
                if(!vis[i]){
                    queue.add(new int[]{i, step});
                    vis[i] = true;
                }
            }
            // 将对应数组从哈希表中删除
            hashMap.remove(arr[index]);
        }
    }
    return ans;
}

1332. 删除回文子序列

给你一个字符串 s，它仅由字母 ‘a’ 和 ‘b’ 组成。每一次删除操作都可以从 s 中删除一个回文子序列。
返回删除给定字符串中所有字符（字符串为空）的最小删除次数。
「子序列」定义：如果一个字符串可以通过删除原字符串某些字符而不改变原字符顺序得到，那么这个字符串就是原字符串的一个子序列。
「回文」定义：如果一个字符串向后和向前读是一致的，那么这个字符串就是一个回文。

示例 ：

输入：s = "baabb"
输出：2
解释："baabb" -> "b" -> "". 
先删除回文子序列 "baab"，然后再删除 "b"。

提示：

• 1 <= s.length <= 1000
• s 仅包含字母 ‘a’ 和 ‘b’

解题思路：如果字符串s是回文串，则只需要删除一次就可以，如果字符串s不是回文串，s串可以分为两个回文子串，即所有的 ‘a’ 和 所有的 ‘b’，删除两次即可。

public int removePalindromeSub(String s) {
    int i,j;
    i = 0;
    j = s.length()-1;
    while(i < j){
    	// 判断是否为回文串，不是则返回2
        if(s.charAt(i) != s.charAt(j)){
            return 2;
        }
        i++;
        j--;
    }
    // 回文串，则返回1
    return 1;
}

2034. 股票价格波动

给你一支股票价格的数据流。数据流中每一条记录包含一个时间戳和该时间点股票对应的价格 。
不巧的是，由于股票市场内在的波动性，股票价格记录可能不是按时间顺序到来的。某些情况下，有的记录可能是错的。如果两个有相同时间戳的记录出现在数据流中，前一条记录视为错误记录，后出现的记录更正前一条错误的记录。
请你设计一个算法，实现：
更新股票在某一时间戳的股票价格，如果有之前同一时间戳的价格，这一操作将更正之前的错误价格。

• 找到当前记录里最新股票价格 。最新股票价格定义为时间戳最晚的股票价格。
• 找到当前记录里股票的最高价格 。
• 找到当前记录里股票的最低价格 。

请你实现 StockPrice 类：

• StockPrice() 初始化对象，当前无股票价格记录。
• void update(int timestamp, int price) 在时间点 timestamp 更新股票价格为 price 。
• int current() 返回股票 最新价格 。
• int maximum() 返回股票 最高价格 。
• int minimum() 返回股票 最低价格 。

示例：

输入：
["StockPrice", "update", "update", "current", "maximum", "update", "maximum",
 "update", "minimum"]
[[], [1, 10], [2, 5], [], [], [1, 3], [], [4, 2], []]
输出：
[null, null, null, 5, 10, null, 5, null, 2]

解释：
StockPrice stockPrice = new StockPrice();
stockPrice.update(1, 10); // 时间戳为 [1] ，对应的股票价格为 [10] 。
stockPrice.update(2, 5);  // 时间戳为 [1,2] ，对应的股票价格为 [10,5] 。
stockPrice.current();     // 返回 5 ，最新时间戳为 2 ，对应价格为 5 。
stockPrice.maximum();     // 返回 10 ，最高价格的时间戳为 1 ，价格为 10 。
stockPrice.update(1, 3);  // 之前时间戳为 1 的价格错误，价格更新为 3 。
                          // 时间戳为 [1,2] ，对应股票价格为 [3,5] 。
stockPrice.maximum();     // 返回 5 ，更正后最高价格为 5 。
stockPrice.update(4, 2);  // 时间戳为 [1,2,4] ，对应价格为 [3,5,2] 。
stockPrice.minimum();     // 返回 2 ，最低价格时间戳为 4 ，价格为 2 。

提示：

• 1 <= timestamp, price <= 10⁹
• update，current，maximum 和 minimum 总 调用次数不超过 10⁵ 。
• current，maximum 和 minimum 被调用时，update操作至少已经被调用过 一次 。

解题思路：使用哈希表存放时间和对应的价格，并完成更新价格。使用treemap对价格进行排序。

class StockPrice {
	// cur 保存最大的时间戳
    int cur;
    // 哈希表
    Map<Integer, Integer> map = new HashMap<>();
    // treeMap 排序,key为价格，value价格出现的次数
    TreeMap<Integer, Integer> ts = new TreeMap<>();
    public void update(int timestamp, int price) {
    	// 保存最大时间戳
        cur = Math.max(cur, timestamp);
        // 判断是否已经包含这个时间戳
        if (map.containsKey(timestamp)) {
        	// 更新值
            int old = map.get(timestamp);
            // 得到该值对应次数
            int cnt = ts.get(old);
            // 次数为1，删除，否则次数减1
            if (cnt == 1) ts.remove(old);
            else ts.put(old, cnt - 1);
        }
        // 存入值
        map.put(timestamp, price);
        // 存入ts中
        ts.put(price, ts.getOrDefault(price, 0) + 1);
    }
    
    public int current() {
    	// 返回时间戳对应的值
        return map.get(cur);
    }
    
    public int maximum() {
    	// 返回最大的价格
        return ts.lastKey();
    }
    
    public int minimum() {
    	// 返回最小的价格
        return ts.firstKey();
    }
}

2045. 到达目的地的第二短时间

城市用一个 双向连通 图表示，图中有 n 个节点，从 1 到 n 编号（包含 1 和 n）。图中的边用一个二维整数数组 edges 表示，其中每个 edges[i] = [ui, vi] 表示一条节点 ui 和节点 vi 之间的双向连通边。每组节点对由最多一条边连通，顶点不存在连接到自身的边。穿过任意一条边的时间是time分钟。

每个节点都有一个交通信号灯，每 change 分钟改变一次，从绿色变成红色，再由红色变成绿色，循环往复。所有信号灯都同时改变。你可以在任何时候进入某个节点，但是只能在节点信号灯是绿色时 才能离开。如果信号灯是绿色 ，你不能在节点等待，必须离开。

第二小的值是严格大于最小值的所有值中最小的值。

注意：

• 你可以任意次穿过任意顶点，包括1和n。
• 你可以假设在启程时，所有信号灯刚刚变成绿色。

给你n、edges、time和change，返回从节点1到节点n需要的第二短时间。

示例：

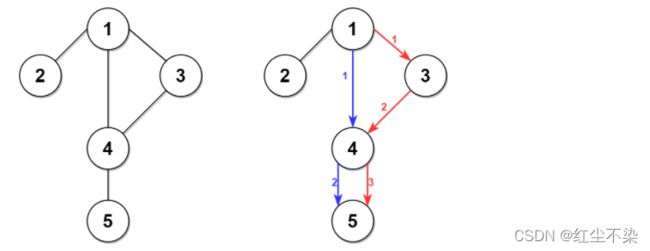
输入：n = 5, edges = [[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5
输出：13
解释：
上面的左图展现了给出的城市交通图。
右图中的蓝色路径是最短时间路径。
花费的时间是：
- 从节点 1 开始，总花费时间=0
- 1 -> 4：3 分钟，总花费时间=3
- 4 -> 5：3 分钟，总花费时间=6
因此需要的最小时间是 6 分钟。

右图中的红色路径是第二短时间路径。
- 从节点 1 开始，总花费时间=0
- 1 -> 3：3 分钟，总花费时间=3
- 3 -> 4：3 分钟，总花费时间=6
- 在节点 4 等待 4 分钟，总花费时间=10
- 4 -> 5：3 分钟，总花费时间=13
因此第二短时间是 13 分钟。      

输入：n = 2, edges = [[1,2]], time = 3, change = 2
输出：11
解释：
最短时间路径是 1 -> 2 ，总花费时间 = 3 分钟
最短时间路径是 1 -> 2 -> 1 -> 2 ，总花费时间 = 11 分钟

解题思路：BFS，构建图（无向边），每个边的权重都是一样的，设为1，通过BFS，找出节点 1到每个点的最短路径和次短路径。最后根据 节点1到节点n的次短路径算出时间。时间包括等待时间。
时间为time如果tiem%2change的值为 [change,2change)之间 ，则 等待时间为 twait = change - time%change;

public int secondMinimum(int n, int[][] edges, int time, int change) {
    // 构建图
    List<Integer>[] graph = new List[n];
    for(int i = 0; i < n; i++){
        graph[i] = new ArrayList<>();
    }
    for(int[] edge : edges){
        graph[edge[0] - 1].add(edge[1]);
        graph[edge[1] - 1].add(edge[0]);
    }
    // path[i][0] 为 节点 1 到 节点 i 的最短路径，path[i][1] 为节点 1到节点 i 的次短路径
    int[][] path = new int[n][2];
    for(int i = 0; i < n; i++){
        Arrays.fill(path[i], Integer.MAX_VALUE);
    }
    // 到自己的最短路径为 0
    path[0][0] = 0;
    Queue<int[]> queue = new ArrayDeque<>();
    queue.offer(new int[]{1, 0});
    while(path[n - 1][1] == Integer.MAX_VALUE){
        int[] arr = queue.poll();
        // 到节点 cur 的距离为 len
        int cur = arr[0], len = arr[1];
        // 求解与 cur 相邻的节点的距离
        for(int next : graph[cur - 1]){
            // 更新距离
            if(len + 1 < path[next - 1][0]){
                // 更新为最小距离
                path[next - 1][0] = len + 1;
                queue.offer(new int[]{next, len + 1});
            }else if(len + 1 > path[next - 1][0] && len + 1 < path[next - 1][1]){
                // 更新为次小距离
                path[next - 1][1] = len + 1;
                queue.offer(new int[]{next, len + 1});
            }
        }
    }
    // 根据次短距离求解时间
    int ans = 0;
    for(int i = 0; i < path[n-1][1]; i++){
        if(ans % (2 * change) >= change){
            ans += change - ans%change;
        }
        ans = ans + time;
    }
	// 返回最终结果
    return ans;
}

1688. 比赛中的配对次数

给你一个整数 n ，表示比赛中的队伍数。比赛遵循一种独特的赛制：

• 如果当前队伍数是 偶数 ，那么每支队伍都会与另一支队伍配对。总共进行 n / 2 场比赛，且产生 n / 2 支队伍进入下一轮。
• 如果当前队伍数为 奇数 ，那么将会随机轮空并晋级一支队伍，其余的队伍配对。总共进行 (n - 1) / 2 场比赛，且产生 (n - 1) / 2 + 1 支队伍进入下一轮。

返回在比赛中进行的配对次数，直到决出获胜队伍为止。

示例：

输入：n = 14
输出：13
解释：比赛详情：
- 第 1 轮：队伍数 = 14 ，配对次数 = 7 ，7 支队伍晋级。
- 第 2 轮：队伍数 = 7 ，配对次数 = 3 ，4 支队伍晋级。 
- 第 3 轮：队伍数 = 4 ，配对次数 = 2 ，2 支队伍晋级。
- 第 4 轮：队伍数 = 2 ，配对次数 = 1 ，决出 1 支获胜队伍。
总配对次数 = 7 + 3 + 2 + 1 = 13

解题思路：模拟法，模拟匹配晋级过程

public int numberOfMatches(int n) {
    int ans = 0;
    while(n != 1){
        if(n % 2 == 0){
            ans += n/2;
            n = n/2;
        }else{
            ans += (n-1)/2;
            n = (n+1)/2;
        }
    }
    return ans;
}

数学法：匹配一次就淘汰一个队伍，最终淘汰n-1只队伍，也就是品匹配n-1次。

public int numberOfMatches(int n) {
    return n-1;
}

2013. 检测正方形

给你一个在 X-Y 平面上的点构成的数据流。设计一个满足下述要求的算法：

• 添加一个在数据流中的新点到某个数据结构中。可以添加重复的点，并会视作不同的点进行处理。
• 给你一个查询点，请你从数据结构中选出三个点，使这三个点和查询点一同构成一个面积为正的轴对齐正方形，统计满足该要求的方案数目。

轴对齐正方形是一个正方形，除四条边长度相同外，还满足每条边都与x-轴或y-轴平行或垂直。

实现DetectSquares类：

• DetectSquares() 使用空数据结构初始化对象
• void add(int[] point) 向数据结构添加一个新的点 point = [x, y]
• int count(int[] point) 统计按上述方式与点 point = [x, y] 共同构造轴对齐正方形的方案数。

示例：

输入：
["DetectSquares", "add", "add", "add", "count", "count", "add", "count"]
[[], [[3, 10]], [[11, 2]], [[3, 2]], [[11, 10]], [[14, 8]], [[11, 2]], [[11, 10]]]
输出：
[null, null, null, null, 1, 0, null, 2]

解释：
DetectSquares detectSquares = new DetectSquares();
detectSquares.add([3, 10]);
detectSquares.add([11, 2]);
detectSquares.add([3, 2]);
detectSquares.count([11, 10]); // 返回 1 。你可以选择：
                               //   - 第一个，第二个，和第三个点
detectSquares.count([14, 8]);  // 返回 0 。查询点无法与数据结构中的这些点构成正方形。
detectSquares.add([11, 2]);    // 允许添加重复的点。
detectSquares.count([11, 10]); // 返回 2 。你可以选择：
                               //   - 第一个，第二个，和第三个点
                               //   - 第一个，第三个，和第四个点

提示：

• point.length == 2
• 0 <= x, y <= 1000
• 调用add 和count 的总次数最多为5000

解题思路：使用哈希表存储点和对应的点的个数。
哈希表结构为 Map> cnt，key为对应y坐标，value中为map，map中的key为对应 x坐标，value为 点（x,y）的次数。
计算 count 的思路：从所有点中依次寻找，不和目标点同一列的所有点，通过计算得到边长，通过边长确定其余三个点，然后得到三个点的出现次数，相乘为组成正方形的数量。

class DetectSquares {
    //map(y,(x,cut))map中key为y的坐标，value为map，map的key为x的坐标和(x,y)坐标的点个数。
    Map<Integer, Map<Integer, Integer>> cnt;
    
    public DetectSquares() {
        cnt = new HashMap<>();
    }

    public void add(int[] point) {
        // 将(x,y)点加入
        int x = point[0], y = point[1];
        // 如果没有键y对应的值，则与给定的新的hashMap绑定。
        cnt.putIfAbsent(y, new HashMap<>());
        // 根据y值得到对应的值。
        Map<Integer, Integer> yCnt = cnt.get(y);
        // 加入x值，并刷新对应的次数
        yCnt.put(x, yCnt.getOrDefault(x, 0) + 1);
    }

    public int count(int[] point) {
        int res = 0;
        int x = point[0], y = point[1];
        // 当前点所在的 y，没有其它点，返回 0
        if(!cnt.containsKey(y)){
            return 0;
        }
        // 根据y得到对应的map，map中为y列中其它的所有点
        Map<Integer,Integer> yCnt = cnt.get(y);
        Set<Map.Entry<Integer,Map<Integer,Integer>>> entries = cnt.entrySet();
        for(Map.Entry<Integer, Map<Integer, Integer>> entry : entries){
            // col为y值
            int col = entry.getKey();
            // 对应的x值和次数
            Map<Integer, Integer> colCnt = entry.getValue();
            // col不和目标点为同一列
            if(col != y){
                // d为边长，通过计算得到。
                int d = col - y;
                // 从 yCnt中找出一个点，从 colCnt中找出两个点，将点出现的个数相乘
                res += colCnt.getOrDefault(x, 0) * 
                	   yCnt.getOrDefault(x + d, 0) * 
                	   colCnt.getOrDefault(x + d, 0);
                res += colCnt.getOrDefault(x, 0) * 
                	   yCnt.getOrDefault(x - d, 0) * 
                	   colCnt.getOrDefault(x - d, 0);
            }
        }
        return res;
    }
}