原子范数初探:以到达角估计为例
到达方向(Direction-of-arrival, DOA)估计是指从形成传感器阵列的多个接收天线的输出中检索若干电磁波/源的方向信息的过程。DOA估计是阵列信号处理中的一个主要问题,在雷达、声纳、无线通信中有着广泛的应用。
基本数学模型
考虑 K K K个窄带的远场源信号 s k , k = 1 , ⋯ , K s_k, k=1,\cdots, K sk,k=1,⋯,K,多个接收阵列从不同方向 { θ k } k = 1 K {\{\theta_k\}}_{k=1}^K {θk}k=1K接收到信号。而不同阵列之间的信号延时可以用简单的相移(phase shift)来表征,这也就引出来下面的信号模型:
y ( t ) = ∑ k = 1 K a ( θ k ) s k ( t ) + e ( t ) = A ( θ ) s ( t ) + e ( t ) , t = 1 , ⋯ , L (1) \boldsymbol y(t) = \sum_{k=1}^K \boldsymbol a(\theta_k) s_{k}(t) + \boldsymbol e(t) = \boldsymbol A(\boldsymbol \theta) \boldsymbol s(t) + \boldsymbol e(t), \ \ t = 1,\cdots, L \tag{1} y(t)=k=1∑Ka(θk)sk(t)+e(t)=A(θ)s(t)+e(t), t=1,⋯,L(1)
其中 t t t表示第 t t t个时隙(snapshot), L L L表示总的时隙数量(the number of snapshots)。 y ( t ) ∈ C M × 1 \boldsymbol y(t) \in \mathbb C^{M \times 1} y(t)∈CM×1, s ( t ) ∈ C K × 1 \boldsymbol s(t) \in \mathbb C^{K \times 1} s(t)∈CK×1, e ( t ) ∈ C M × 1 \boldsymbol e(t) \in \mathbb C^{M \times 1} e(t)∈CM×1分别表示阵列在第 t t t个时隙的输出信号,源信号向量,以及测量噪声。 M M M是阵列的数量。 a ( θ k ) \boldsymbol a(\theta_k) a(θk)被称作第 k k k个信号源的导向矢量(steering vector),这 K K K个导向矢量构成了阵列流形矩阵(array manifold matrix) A ( θ ) = [ a ( θ 1 ) , ⋯ , a ( θ K ) ] ∈ C M × K \boldsymbol A(\boldsymbol \theta)=\left [ \boldsymbol a(\theta_1), \cdots, \boldsymbol a(\theta_K) \right] \in \mathbb C^{M \times K} A(θ)=[a(θ1),⋯,a(θK)]∈CM×K。我们可以把式(1)写为更紧凑的矩阵形式:
Y = A ( θ ) S + E (2) \boldsymbol Y = \boldsymbol A(\boldsymbol \theta) \boldsymbol S + \boldsymbol E \tag{2} Y=A(θ)S+E(2)
给定接收信号 Y ∈ C M × L \boldsymbol Y \in \mathbb C^{M \times L} Y∈CM×L,以及映射 θ → a ( θ ) \theta \rightarrow \boldsymbol a(\theta) θ→a(θ),我们的目标是估计出参数 { θ k } k = 1 K {\{\theta_k\}}_{k=1}^K {θk}k=1K(即DOAs)。另外,在实际模型中,我们一般没有 K K K的先验知识,且我们一般假设 K ≤ M K \leq M K≤M。
阵列的几何结构
我们考虑一个简单的线性阵列(linear array),如下图所示
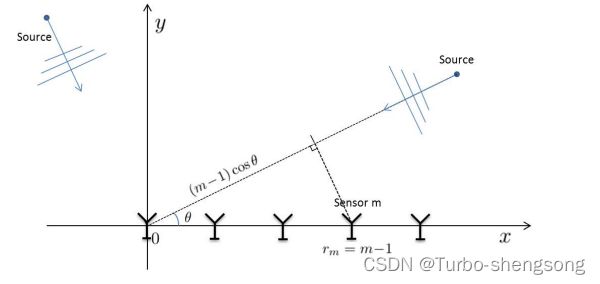
a ( θ ) ∈ C M × 1 \boldsymbol a(\theta) \in \mathbb C^{M \times 1} a(θ)∈CM×1表示为:
a m ( θ ) = e i π r m cos θ , m = 1 , 2 , ⋯ , M (3) a_m(\theta) = e^{i \pi r_m \cos \theta} \ \ , m=1,2,\cdots,M \tag{3} am(θ)=eiπrmcosθ ,m=1,2,⋯,M(3)
我们可以把变量 θ \theta θ替换为 f = 1 2 cos θ f = \frac{1}{2} \cos \theta f=21cosθ,并且定义(without ambiguity) a ( f ) = a ( arccos ( 2 f ) ) = a ( θ ) \boldsymbol a(f)=\boldsymbol a \left( \arccos(2f) \right)=\boldsymbol a(\theta) a(f)=a(arccos(2f))=a(θ),那么映射 a ( f ) \boldsymbol a(f) a(f)为:
a m ( f ) = e i 2 π r m f , m = 1 , 2 , ⋯ , M (4) a_m(f) = e^{i 2 \pi r_m f}, \ \ m=1,2,\cdots,M \tag{4} am(f)=ei2πrmf, m=1,2,⋯,M(4)
从上式可以看出,空域上的估计问题变成了一个时频估计(temporal frequency estimation)问题(线谱估计问题,linear spectral estimation)。
对时频域的理解:
- 时间:注意到 r m r_m rm其实想表征第 m − 1 m-1 m−1根天线距离第0根天线之间的距离,因为距离与时间的正比关系,所以 r m r_m rm对应到时间(temporal);
- 频率:注意到 f f f的定义域 f ∈ ( − 1 2 , 1 2 ] f \in (-\frac{1}{2}, \frac{1}{2}] f∈(−21,21], 2 π f ∈ ( − π , π ] 2 \pi f \in (- \pi , \pi] 2πf∈(−π,π],类比角频率。我们定义 T = ( − 1 2 , 1 2 ] \mathbb T=(-\frac{1}{2}, \frac{1}{2}] T=(−21,21](之后会用到)
如果我们考虑等间距的线性阵列,那么该阵列即为ULA( Uniform Linear Array ),并且仅考虑最简单的单位时间,即两个相邻天线的时间差归一,对应到 r m − r m − 1 = 1 r_m - r_{m-1}=1 rm−rm−1=1,这时
a ( f ) = [ 1 , e i 2 π f , ⋯ , e i 2 π ( M − 1 ) f ] T ∈ C M × 1 (5) \boldsymbol a(f) = [1, e^{i 2 \pi f}, \cdots, e^{i 2 \pi (M-1) f}]^T \in \mathbb C^{M \times 1} \tag{5} a(f)=[1,ei2πf,⋯,ei2π(M−1)f]T∈CM×1(5)
如果通过仅保留一部分天线,从ULA获得线性阵列,则称为稀疏线性阵列(SLA,Sparse Linear Array)。
ULA模型和SLA模型
ULA模型: M M M根接收天线,则阵列接收信号模型为:
Y = A ( f ) S + E (6) \boldsymbol Y = \boldsymbol A( \boldsymbol f) \boldsymbol S + \boldsymbol E \tag{6} Y=A(f)S+E(6)
其中 f k ∈ T f_k \in \mathbb T fk∈T, k = 1 , ⋯ , K k=1,\cdots,K k=1,⋯,K是我们感兴趣的频率成分,它与DOAs有着one-to-one的映射关系。
SLA模型:SLA有 M M M根接收天线,若这 M M M根天线是从 N N N个ULA阵列中选取的,记索引为 Ω = { Ω 1 , ⋯ , Ω M } \Omega=\{ \Omega_1, \cdots, \Omega_M \} Ω={Ω1,⋯,ΩM},其中 N ≥ M N \geq M N≥M,且 1 ≤ Ω 1 < ⋯ < Ω M ≤ N 1 \leq \Omega_1 < \cdots < \Omega_M \leq N 1≤Ω1<⋯<ΩM≤N,那么SLA的数据模型为
Y Ω = A Ω ( f ) S + E Ω (7) \boldsymbol Y_{\Omega} = \boldsymbol A_{\Omega} (f) \boldsymbol S + \boldsymbol E_{\Omega} \tag{7} YΩ=AΩ(f)S+EΩ(7)
单时隙简单场景(The Single Snapshot Case)
确定性方法的一般框架
SLA中,单时隙场景的数据模型为:
y Ω = z Ω + e Ω , z = A ( f ) s (8) \boldsymbol y_{\Omega} = \boldsymbol z_{\Omega} + \boldsymbol e_{\Omega}, \ \ \boldsymbol z = \boldsymbol A(\boldsymbol f) \boldsymbol s \tag{8} yΩ=zΩ+eΩ, z=A(f)s(8)
ULA是 Ω = { 1 , ⋯ , N } \Omega=\{1,\cdots,N\} Ω={1,⋯,N}的特殊情况。对于确定性的稀疏方法,一般的,我们需要解决下面的约束优化问题:
min z M ( z ) , subject to ∥ z Ω − y Ω ∥ 2 ≤ η (9) \min_{\boldsymbol z} \mathcal M(\boldsymbol z), \ \ \text{subject to } {\Vert \boldsymbol z_{\Omega} - \boldsymbol y_{\Omega} \Vert}_2 \leq \eta \tag{9} zminM(z), subject to ∥zΩ−yΩ∥2≤η(9)
其中噪声是有界的: ∥ e Ω ∥ 2 ≤ η \Vert \boldsymbol e_{\Omega} \Vert_2 \leq \eta ∥eΩ∥2≤η。 M ( z ) \mathcal M(\boldsymbol z) M(z)表征一种稀疏的metric:最小化 M ( z ) \mathcal M(\boldsymbol z) M(z)意味着相应的 a ( f ) \boldsymbol a(f) a(f)的数量(the number of components/atoms a ( f ) \boldsymbol a(f) a(f))降低。这些原子(atoms)可以直接给出频率的估计结果。我们可以考虑下面的正则优化问题(regularized optimization problem):
min z λ M ( z ) + 1 2 ∥ z Ω − y Ω ∥ 2 2 (10) \min_{\boldsymbol z} \lambda \mathcal M(z) + \frac{1}{2} {\Vert \boldsymbol z_{\Omega} - \boldsymbol y_{\Omega} \Vert}^2_2 \tag{10} zminλM(z)+21∥zΩ−yΩ∥22(10)
令 η → 0 \eta \rightarrow 0 η→0,可以得到退化的无噪声问题:
min z M ( z ) , subject to z Ω = y Ω (11) \min_{\boldsymbol z} \mathcal M(\boldsymbol z), \ \ \text{subject to } \boldsymbol z_{\Omega}=\boldsymbol y_{\Omega} \tag{11} zminM(z), subject to zΩ=yΩ(11)
之后的内容,我们主要考虑metric M ( z ) \mathcal M(\boldsymbol z) M(z)的选择。
注:这里的一个原子(atoms)指的是一个频率成分,即对应到一个 a ( f ) \boldsymbol a(f) a(f)
原子 ℓ 0 \ell_0 ℓ0范数(Atomic ℓ 0 \ell_0 ℓ0 norm)
我们定义原子集合(the set of atoms):
A = { a ( f , ϕ ) = a ( f ) ϕ : f ∈ T , ϕ ∈ C , ∣ ϕ ∣ = 1 } (12) \mathcal A = \{ \boldsymbol a(f, \phi) = \boldsymbol a(f) \phi : f \in \mathbb T, \phi \in \mathbb C, |\phi|=1\} \tag{12} A={a(f,ϕ)=a(f)ϕ:f∈T,ϕ∈C,∣ϕ∣=1}(12)
真实信号 z \boldsymbol z z是原子集合 A \mathcal A A中 K K K个原子的线性组合,原子 ℓ 0 \ell_0 ℓ0范数(the atomic ℓ 0 \ell_0 ℓ0 (pseudo-) norm),我们用 ∥ z ∥ A , 0 \Vert \boldsymbol z \Vert_{\mathcal A,0} ∥z∥A,0来表示:is defined as the minimum numer of atoms in A \mathcal A A that can synthesize z \boldsymbol z z:
∥ z ∥ A , 0 = inf c k , f k , ϕ k { K : z = ∑ k = 1 K a ( f k , ϕ k ) c k , f k ∈ T , ∣ ϕ k ∣ = 1 , c k > 0 } = inf f k , s k { K : z = ∑ k = 1 K a ( f k ) s k , f k ∈ T } (13) \begin{aligned} \Vert \boldsymbol z \Vert_{\mathcal A,0} &= \inf_{c_k, f_k, \phi_k} \left \{ \mathcal K: \boldsymbol z = \sum_{k=1}^{\mathcal K} \boldsymbol a(f_k, \phi_k) c_k , \ \ f_k \in \mathbb T, \vert \phi_k \vert = 1, c_k > 0 \right \} \\ &= \inf_{f_k, s_k} \left \{ \mathcal K: \boldsymbol z= \sum_{k=1}^{\mathcal K} \boldsymbol a(f_k) s_k, f_k \in \mathbb T \right \} \end{aligned} \tag{13} ∥z∥A,0=ck,fk,ϕkinf{K:z=k=1∑Ka(fk,ϕk)ck, fk∈T,∣ϕk∣=1,ck>0}=fk,skinf{K:z=k=1∑Ka(fk)sk,fk∈T}(13)
为了解决该问题,我们需要引入Toepitz协方差矩阵的范德蒙德分解。更具体一些,令 T ( u ) \boldsymbol T(u) T(u)为Toeplitz矩阵,并且满足下述条件:
[ x z H z T ( u ) ] ≽ 0 (14) \left[ \begin{matrix} x& \boldsymbol{z}^H\\ \boldsymbol{z}& \boldsymbol{T}\left( \boldsymbol{u} \right)\\ \end{matrix} \right] \succcurlyeq \boldsymbol{0} \tag{14} [xzzHT(u)]≽0(14)
其中 ≽ 0 \succcurlyeq \boldsymbol{0} ≽0表示半正定矩阵。 x x x是一个待优化的自由变量,如果式(14)要成立,那么 T ( u ) \boldsymbol T(\boldsymbol u) T(u)必然是一个半正定的Toeplitz矩阵,因此可以进行 rank ( T ( u ) ) \text{rank}(\boldsymbol T(\boldsymbol u)) rank(T(u))-atomic Vandermonde deomposition。另外, z ∈ span ( T ( u ) ) \boldsymbol z \in \text{span}(\boldsymbol T(\boldsymbol u)) z∈span(T(u)),因此原子 ℓ 0 \ell_0 ℓ0范数与 T ( u ) \boldsymbol T(\boldsymbol u) T(u)的秩密切相关,我们有下面的定理
式(13)定义的 ∥ z ∥ A , 0 \Vert \boldsymbol z \Vert_{\mathcal A, 0} ∥z∥A,0,等于下面优化问题的最优值:
min x , u rank ( T ( u ) ) subject to [ x z H z T ( u ) ] ≽ 0 (15) \min_{\boldsymbol x, \boldsymbol u} \text{rank} \left ( \boldsymbol T(\boldsymbol u) \right) \\ \text{subject to} \left[ \begin{matrix} x& \boldsymbol{z}^H\\ \boldsymbol{z}& \boldsymbol{T}\left( \boldsymbol{u} \right)\\ \end{matrix} \right] \succcurlyeq \boldsymbol{0} \tag{15} x,uminrank(T(u))subject to[xzzHT(u)]≽0(15)
原子范数(Atomic Norm)
比原子 ℓ 0 \ell_0 ℓ0范数更为实用的metric是原子范数最小化(Atomic Norm Minimization, ANM),我们正式地引入原子范数,原子范数的实质为式(12)集合中 A \mathcal A A的凸包(convex hull):
∥ z ∥ A = inf { t > 0 : z ∈ t ⋅ c o n v ( A ) } = inf c k , f k , ϕ k { ∑ k c k : z = ∑ k a ( f k , ϕ k ) c k , f k ∈ T , ∣ ϕ k ∣ = 1 , c k > 0 } = inf f k , s k { ∑ k ∣ s k ∣ : z = ∑ k a ( f k ) s k , f k ∈ T } (16) \begin{aligned} \Vert \boldsymbol z \Vert_{\mathcal A} &= \inf \left \{ t > 0: z \in t \cdot conv(\mathcal A) \right \} \\ &= \inf_{c_k, f_k, \phi_k} \left \{ \sum_{k} c_k: \ \ \boldsymbol z=\sum_{k} \boldsymbol a(f_k, \phi_k) c_k ,\ f_k \in \mathbb T, \ \vert \phi_k \vert=1, \ c_k > 0 \right \} \\ &= \inf_{f_k, s_k} \left \{ \sum_{k} \vert s_k \vert: \boldsymbol z = \sum_{k} \boldsymbol a(f_k) s_k, \ \ f_k \in \mathbb T \right \} \end{aligned} \tag{16} ∥z∥A=inf{t>0:z∈t⋅conv(A)}=ck,fk,ϕkinf{k∑ck: z=k∑a(fk,ϕk)ck, fk∈T, ∣ϕk∣=1, ck>0}=fk,skinf{k∑∣sk∣:z=k∑a(fk)sk, fk∈T}(16)
根据定义,我们不难发现,原子范数其实对应到有限维向量的 ℓ 1 \ell_1 ℓ1范数。为了解决原子范数问题,学界和业界提供了一种高效的SDP优化方法。
定理:式(16)中定义的 ∥ z ∥ A \Vert \boldsymbol z \Vert_{\mathcal A} ∥z∥A,等于下面SDP问题的最优值:
min x u 1 2 x + 1 2 u 1 subject to [ x z H z T ( u ) ] ≽ 0 (17) \begin{aligned} & \min_{x \boldsymbol u} \frac{1}{2} x+ \frac{1}{2} u_1 \\ & \text{subject to } \left[ \begin{matrix} x& \boldsymbol{z}^H\\ \boldsymbol{z}& \boldsymbol{T}\left( \boldsymbol{u} \right)\\ \end{matrix} \right] \succcurlyeq \boldsymbol{0} \end{aligned} \tag{17} xumin21x+21u1subject to [xzzHT(u)]≽0(17)
证明:令 F F F为式上述优化问题的最优值,我们需要证明 F = ∥ z ∥ A F=\Vert \boldsymbol z \Vert_{\mathcal A} F=∥z∥A
(1)我们首先证明 F ≤ ∥ z ∥ A F \leq \Vert \boldsymbol z \Vert_{\mathcal A} F≤∥z∥A
令 z = ∑ k c k a ( f k , ϕ k ) = ∑ k a ( f k ) s k \boldsymbol z=\sum_k c_k \boldsymbol a(f_k, \phi_k) = \sum_{k} \boldsymbol a(f_k) s_k z=∑kcka(fk,ϕk)=∑ka(fk)sk表征 z \boldsymbol z z的原子分解形式。然后令 u \boldsymbol u u满足 T ( u ) = ∑ k c k a ( f k ) a H ( f k ) \boldsymbol T( \boldsymbol u ) = \sum_k c_k \boldsymbol a(f_k) \boldsymbol a^H(f_k) T(u)=∑kcka(fk)aH(fk),且 x = ∑ k c k x = \sum_{k} c_k x=∑kck,由此我们可以得到
[ x z H z T ( u ) ] = ∑ k c k [ ϕ k ∗ a ( f k ) ] [ ϕ k ∗ a ( f k ) ] H ≽ 0 (18) \left[ \begin{matrix} x& \boldsymbol{z}^H\\ \boldsymbol{z}& \boldsymbol{T}\left( \boldsymbol{u} \right)\\ \end{matrix} \right] =\sum_k{c_k\left[ \begin{array}{c} \phi _{k}^{*}\\ \boldsymbol{a}\left( f_k \right)\\ \end{array} \right]}\left[ \begin{array}{c} \phi _{k}^{*}\\ \boldsymbol{a}\left( f_k \right)\\ \end{array} \right] ^H \succcurlyeq \boldsymbol{0} \tag{18} [xzzHT(u)]=k∑ck[ϕk∗a(fk)][ϕk∗a(fk)]H≽0(18)
因此,由(18)式构建的 x x x和 u \boldsymbol u u构成了问题(17)的一个可行解,并且目标函数满足:
1 2 x + 1 2 u 1 = ∑ k c k (19) \frac{1}{2} x+ \frac{1}{2} u_1 = \sum_{k} c_k \tag{19} 21x+21u1=k∑ck(19)
由此,我们可以得到: F ≤ ∑ k c k F \leq \sum_{k} c_k F≤∑kck,因为该不等式对 z \boldsymbol z z的任意原子分解都成立,因此 F ≤ ∑ k c k F \leq \sum_{k} c_k F≤∑kck必然成立。
(2)我们证明 F ≥ ∥ z ∥ A F \geq \Vert \boldsymbol z \Vert_{\mathcal A} F≥∥z∥A
假设 ( x ^ , u ^ ) (\hat x, \hat{\boldsymbol u}) (x^,u^)是问题(17)的一个最优解。因为 T ( u ^ ) ≽ 0 \boldsymbol T(\hat{\boldsymbol u}) \succcurlyeq \boldsymbol{0} T(u^)≽0,利用半正定Toeplitz矩阵的范德蒙德分解中的定理,我们得到 T ( u ^ ) \boldsymbol T(\hat{\boldsymbol u}) T(u^)可以进行范德蒙德分解,将分解结果记为 ( r ^ , p ^ k , f ^ k ) (\hat{r}, \hat{p}_k, \hat{f}_k) (r^,p^k,f^k)。另外,因为 [ x ^ z H z T ( u ^ ) ] ≽ 0 \left[ \begin{matrix} \hat x& \boldsymbol{z}^H\\ \boldsymbol{z}& \boldsymbol{T}\left(\hat{ \boldsymbol{u} }\right)\\ \end{matrix} \right] \succcurlyeq \boldsymbol{0} [x^zzHT(u^)]≽0,可以得到 z ∈ span ( T ( u ^ ) ) \boldsymbol z \in \text{span}(\boldsymbol T(\hat{\boldsymbol u})) z∈span(T(u^)),又因为 span ( T ( u ^ ) ) = span ( a ( f 1 ) , ⋯ , a ( f r ^ ) ) \text{span}(T(\hat{\boldsymbol u}))=\text{span}\left ( \boldsymbol a(f_1), \cdots, \boldsymbol a(f_{\hat{r}}) \right) span(T(u^))=span(a(f1),⋯,a(fr^)),我们知道
z = ∑ k = 1 r ^ c ^ k a ( f ^ k , ϕ ^ k ) = ∑ k = 1 r ^ a ( f ^ k ) s ^ k (20) \boldsymbol z = \sum_{k=1}^{\hat r} \hat{c}_k \boldsymbol a( \hat{f}_k, \hat{\phi}_k) = \sum_{k=1}^{\hat r} \boldsymbol a( \hat{f}_k) \hat{s}_k \tag{20} z=k=1∑r^c^ka(f^k,ϕ^k)=k=1∑r^a(f^k)s^k(20)
又因为 [ x ^ z H z T ( u ^ ) ] ≽ 0 \left[ \begin{matrix} \hat x& \boldsymbol{z}^H\\ \boldsymbol{z}& \boldsymbol{T}\left( \hat{\boldsymbol{u} }\right)\\ \end{matrix} \right] \succcurlyeq \boldsymbol{0} [x^zzHT(u^)]≽0,
x ^ ≥ z H [ T ( u ^ ) ] † z = ∑ k = 1 r ^ c ^ k 2 p ^ k u ^ 1 = ∑ k = 1 r ^ p ^ k (21) \begin{aligned} \hat{x} & \geq \boldsymbol z^H [ \boldsymbol{T}\left( \hat{\boldsymbol{u} } \right) ]^{\dagger} \boldsymbol z = \sum_{k=1}^{\hat r} \frac{ \hat c^2_k } { \hat p_k } \\ \hat{u}_1 &= \sum_{k=1}^{\hat r} \hat{p}_k \end{aligned} \tag{21} x^u^1≥zH[T(u^)]†z=k=1∑r^p^kc^k2=k=1∑r^p^k(21)
由此可以得到
F = 1 2 x ^ + 1 2 u ^ 1 ≥ 1 2 ∑ k c ^ k 2 p ^ k + 1 2 ∑ k p ^ k ≥ ∑ k c k ≥ ∥ z ∥ A (22) \begin{aligned} F &= \frac{1}{2} \hat{x} + \frac{1}{2} \hat{u}_1 \\ & \geq \frac{1}{2} \sum_{k} \frac{ \hat c^2_k } { \hat p_k } + \frac{1}{2} \sum_k \hat{p}_k \\ & \geq \sum_k c_k \\ & \geq \Vert \boldsymbol z \Vert_{\mathcal A} \end{aligned} \tag{22} F=21x^+21u^1≥21k∑p^kc^k2+21k∑p^k≥k∑ck≥∥z∥A(22)
结合(1)和(2),我们得到: F = ∥ z ∥ A F=\Vert \boldsymbol z \Vert_{\mathcal A} F=∥z∥A。根据式(22),只有当 p ^ k = c ^ k = ∣ s ^ k ∣ \hat p_k =\hat c_k = \vert \hat s_k \vert p^k=c^k=∣s^k∣,且 ∥ z ∥ A = ∑ k c ^ k = ∑ k ∣ s ^ k ∣ \Vert \boldsymbol z \Vert_{\mathcal A}=\sum_{k} \hat c_k =\sum_k \vert \hat s_k \vert ∥z∥A=∑kc^k=∑k∣s^k∣时取等。因此,式(20)所示的原子分解可以直接得到原子范数。
优化问题(15)与优化问题(17)的关系:(17)中的SDP优化问题本质上是式(15)秩最小化问题的凸松弛。具体来讲,式(17)中目标函数的第二项 1 2 u 1 \frac{1}{2} u_1 21u1是半正定Toeplitz矩阵 T ( u ) \boldsymbol T(\boldsymbol u) T(u)的核范数(所有奇异值之和)或者trace norm (up to a scaling factor),which is a commonly used convex relaxation of the matrix rank。而第一项 1 2 x \frac{1}{2} x 21x是为了防止平凡解(trivial solution)的出现设置的正则项。
关于问题求解过程的总结:
S1: the frequencies component are encoded in the Toeplitz matrix T ( u ) \boldsymbol T(\boldsymbol u) T(u)
S2: Present the SDP optimization problem, and solve SDP. It follows that u \boldsymbol u u is derived, i.e. T ( u ) \boldsymbol T(\boldsymbol u) T(u) is obtained.
S3: Once the resulting SDP problem is solved, the frequencies can be retrieved from the Vandermonde decomposition of T ( u ) \boldsymbol T(\boldsymbol u) T(u)
另外,与原子 ℓ 0 \ell_0 ℓ0范数类似,原子范数也可以被看作是基于协方差的方法,两者的不同之处在于原子 ℓ 0 \ell_0 ℓ0范数直接利用了低秩性,而利用原子范数,问题更容易求解。
参考
[1] Yang, Z., Li, J., Stoica, P., & Xie, L. (2016). Sparse Methods for Direction-of-Arrival Estimation. ArXiv, abs/1609.09596.