第十届蓝桥杯真题题解
目录
一、组队(DFS)
二、年号字串(进制转换)
三、数列求值
四、数的分解
五、迷宫(BFS)
六、特别数的和(暴力)
七、完全二叉树的权值
一、组队(DFS)
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
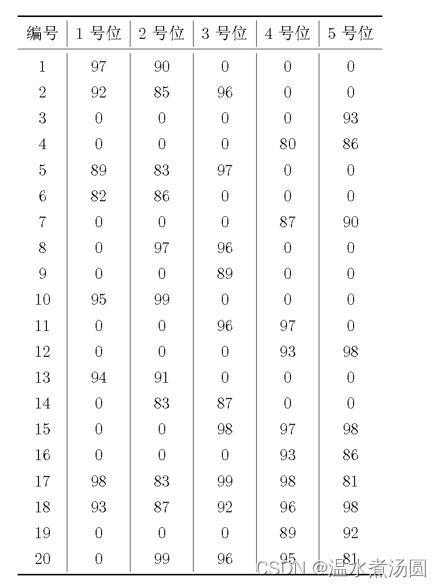
作为篮球队教练,你需要从以下名单中选出 11 号位至 55 号位各一名球员,组成球队的首发阵容。
每位球员担任 1 号位至 5 号位时的评分如下表所示。请你计算首发阵容 1 号位至 5 号位的评分之和最大可能是多少?
答案
490
思路
首先我们需要理解清楚题意,这道题目不是单纯的我们找出每一号位置上的最大值,然后相加就可以求出最后的结果的。因为每一位球员都只能在一个位置上,即使他在每一个位置上的评分都是100分,我们也不可能5个位置都选他。
因此我们在选择的时候就需要有所取舍,最终我们要选出来的是5个位置上的队员的评分最高的一组作为我们的首发阵容。
本道题我们采用的是DFS,DFS最重要的是搜索的顺序。顺序:我们依次对每一个位置考虑,第一个位置有20种选择,然后递归到第二个位置,依次类推。当我们处理完所有的5个位置的时候,我们就得到了一组解,这时,我们需要进行一下判断,如果当前的答案大于我们的res,我们就更新它。最终,我们求解完所有的方案的时候,最大值也就出来了。
#include
#include
#include
#include
using namespace std;
int a[21][6], res;
bool st[21]; //用来标记一下这个人我们是否已经选过了
void dfs(int u, int sum)
{
if(u > 5)
{
if(sum > res) res = sum;
return;
}
//对于每一个位置,依次去枚举一下这20个人
for(int i = 1; i <= 20; i ++ )
if(!st[i]) //如果这个人没有选过的话
{
st[i] = true;
dfs(u + 1, sum + a[i][u]);
st[i] = false;
}
}
int main()
{
for(int i = 1; i <= 20; i ++ )
for(int j = 0; j <= 5; j ++ )
cin >> a[i][j];
dfs(1, 0); //传进去的参数有两个:选到第几个位置了,当前的总分是多少
cout << res;
return 0;
} 注意:在运行上述程序的时候,是需要自己拷贝数据的运行的,因此在蓝桥杯的题库中运行是显示错误(它默认你已经导入了数据)。
二、年号字串(进制转换)
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小明用字母 A 对应数字 1,B 对应 2,以此类推,用 Z 对应 26。对于 27 以上的数字,小明用两位或更长位的字符串来对应,例如 AA 对应 27,AB 对应 28,AZ 对应 52,LQ 对应 329。
请问 2019 对应的字符串是什么?
答案
BYQ
思路
本题其实不是一个26进制的转换。但是我们可以把它看成一个26进制来解决问题,会发现答案完全相符。
因此在调程序的时候,我是手动一个一个调出来的,但其实还可以按照10进制转化为k进制的方法自己算一下,这个可能会更快一点。
手动调代码
#include
#include
#include
#include
using namespace std;
int res;
int main()
{
res = 2 * 26 * 26 + 25 * 26 + 17;
cout << res << endl;
return 0;
} 三、数列求值
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
给定数列 1, 1, 1, 3, 5, 9, 17, ⋯,从第 4 项开始,每项都是前 3 项的和。
求第 20190324 项的最后 4 位数字。
答案
4659
思路
这道题目关键就是要考虑清楚数据范围。20190324是一个非常庞大的数,可想而知,由于每一项都是前3项的和,因此第20190324项是肯定会爆int的。我本来以为long long就不会了,但将第20190324项输出后,发现结果为负,这说明数据溢出了,也就是说int和long long都存不下来这么大的数。
由于题目提到了我们只需要最后4位数,因此我们应该想到这道题目主要考察的就是我们的取余运算。
(a + b) % p = (a % p + b % p) % p
#include
#include
#include
#include
using namespace std;
const int N = 20190440;
int a[N];
int main()
{
a[1] = a[2] = a[3] = 1;
for(int i = 4; i <= 20190324; i ++ )
a[i] = (a[i - 1] + a[i - 2] + a[i - 3]) % 10000;
cout << a[20190324]<< endl;
return 0;
} 四、数的分解
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
把 2019 分解成 3 个各不相同的正整数之和,并且要求每个正整数都不包含数字 2 和 4,一共有多少种不同的分解方法?
注意交换 3 个整数的顺序被视为同一种方法,例如 1000+1001+18 和 1001+1000+18 被视为同一种。
答案
40785
思路
对于这道题,我们只需要逐个枚举每一个位置上的选择就可以了。这里,我采用的是最暴力的方法,就是每个位置上都有2019种选择。
这样的话,就一定会出现题目种所说的3个整数的顺序交换被视为不同的方法,处理这一点,我们只需要将总的方案数除以6就可以了。
为什么是6?因为为了保证不重复,第一个位置有三种选择,第二个位置有2种选择,第三个位置只有1个选择, 3 * 2 * 1 = 6。
本道题易忽略的一点是:
我们需要剔除掉三个数字中有重复数字的方案。
#include
using namespace std;
int res;
bool check(int x)
{
while(x)
{
if(x % 10 == 2 || x % 10 == 4) return false;
x /= 10;
}
return true;
}
int main()
{
for(int i = 1; i <= 2019; i ++ )
for(int j = 1; j <= 2019; j ++ )
for(int k = 1; k <= 2019; k ++ )
{
if(i + j + k != 2019) continue;
if(i == j || i == k || j == k) continue;
//说明i + j + k = 2019,紧接着我们就来判断一下其中是否含有2或4
if(check(i) && check(j) && check(k))
res ++;
}
cout << res / 6 << endl;
return 0;
} 五、迷宫(BFS)
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
下图给出了一个迷宫的平面图,其中标记为 1 的为障碍,标记为 0 的为可以通行的地方。
010000
000100
001001
110000迷宫的入口为左上角,出口为右下角,在迷宫中,只能从一个位置走到这个它的上、下、左、右四个方向之一。
对于上面的迷宫,从入口开始,可以按 DRRURRDDDR 的顺序通过迷宫, 一共 10 步。其中 D、U、L、R 分别表示向下、向上、向左、向右走。 对于下面这个更复杂的迷宫(30 行 50 列),请找出一种通过迷宫的方式,其使用的步数最少,在步数最少的前提下,请找出字典序最小的一个作为答案。
请注意在字典序中 D 答案 一共是186步 DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDD 思路 简单的BFS通常只能输出起点到终点的最短距离,却没有办法输出最短的路径。因此,在这里我想介绍一种BFS输出最短路径的方法。 我们可以先从终点倒着进行一遍BFS,求出每个点到终点的距离存储在d[]数组中。则起点到终点的最短距离就是d[0][0]。然后,我们就正着遍历一遍,判断一下下一步到终点的最短距离是否等于上一步到终点的最短距离,如果等于则说明下一步在最短路径上。 题目描述 小明对数位中含有 2、0、1、9 的数字很感兴趣(不包括前导 0),在 1 到 40 中这样的数包括 1、2、9、10 至 32、39 和 40,共 28 个,他们的和是 574。 请问,在 1 到 n 中,所有这样的数的和是多少? 输入描述 输入一行包含一个整数 n(1 ≤ n ≤ 输出描述 输出一行,包含一个整数,表示满足条件的数的和。 思路 依次枚举1 ~ n之间的每一个数,判断一下其中是否含有数字2、0、1、9中的任何一个数。对其中满足条件的数求和。 题目描述 给定一棵包含 N 个节点的完全二叉树,树上每个节点都有一个权值,按从上到下、从左到右的顺序依次是 现在小明要把相同深度的节点的权值加在一起,他想知道哪个深度的节点权值之和最大?如果有多个深度的权值和同为最大,请你输出其中最小的深度。 注:根的深度是 1。 输入描述 第一行包含一个整数 N(1 ≤ N ≤ 第二行包含 N 个整数 输出描述 输出一个整数代表答案。 思路 最简单的思路就是逐层求和,需要用到双层for循环。第一层for循环用来循环深度和每一层的元素的个数,第二层for循环用来将每一层循环中的数加总求和。最后判断一下当前的和是否大于maxs,如果大于,则更新maxs和depth。01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010001001000100010101
10100001000110010001000010101001010101011111010010
00000100101000000110010100101001000001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000/*
这道题目考察的是BFS求最短路的问题
因为要求字典序最小,因此我们可以把拓展的顺序按照
题目要求的字典序
最终需要输出的是一段字符串
*/
#include 六、特别数的和(暴力)
![]() )。
)。#include 七、完全二叉树的权值
![]() ,
, ![]() , ···,
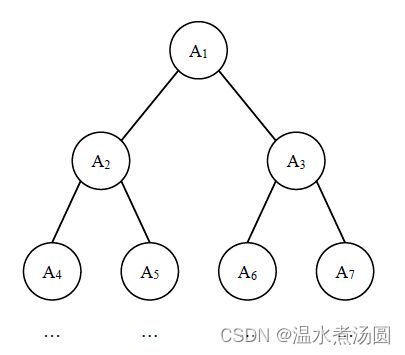
, ···, ![]() ,如下图所示:
,如下图所示:![]() )。
)。![]() ,
, ![]() , ···
, ··· ![]() (−
(−![]() <=
<= ![]() <=
<= ![]() )。
)。/*
暴力:
我们可以先开一个maxs,初始化为一个极小值
因为本题中权值存在负数,因此maxs初始化为负无穷
然后对每一层求和,如果当前层数的和大于res,我们就更新res,
并存储下来当前的深度
每一层的起始坐标和终点坐标也非常好计算,为2^i ~ 2^(i+1)-1
*/
#include