最小费用流的最短路径算法和Ford单源最短路径算法(图解)
屈婉玲《算法设计与分析》第2版第7章网络流算法学习笔记。
概述
最小费用流的负回路算法,是先任意分配流量v0,再将流量调整到权值较小的边上,参考:
基于Floyd算法的最小费用流的负回路算法(图解)
而最小费用流的最短路径算法,则是从0流开始,往最短路径上分配流量,直到流量达到v0为止。
最小费用流的最短路径算法图例
容量-费用网络,初始分配0流:

找出残余容量网络上的最短路径:s->2->t(距离为4),分配5个单位流量,得到f1:

更新残余网络找出最短路径:s->1->2->t (距离为5),分配1个单位流量,得到f2:

更新残余网络找出最短路径:s->1->t (距离为6),分配2个单位流量(v0-f2=2),得到f3:
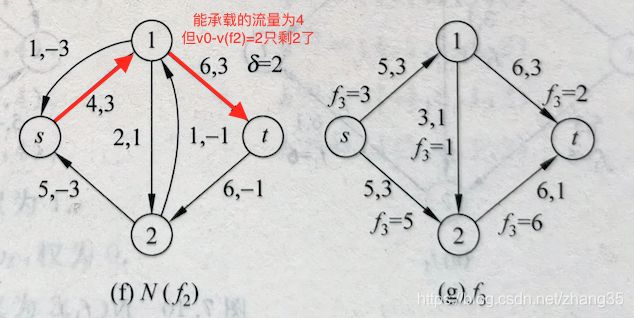
至此流量达到v0,f3即为所求。
伪代码
1. f ← 0
2. 构造N(f)
3. 调用Floyd算法计算N(f)中s-t最短路径
4. if N(f)无s-t路径 then return “无流量v0的可行流” //f是最大流,且v(f)
5. 在N(f)的s-t增广路径中找出最短路径
6. 为最短路径尽可能分配流量,且不超过v0,f ← f1
7. if v(f)<v0 then goto 2
8. return f
Ford算法
上面算法中找最短路径时,使用L.R.Ford 提出的 Ford 算法替代Floyd算法更好,因为只需求单源最短路径。Ford算法可以求无负回路的赋权有向图中单源最短路径(和Dijkstra条件和功能一样)。
设赋权有向图D=
使用动态规划法,记d(k)(i)为D中v1到vi边数不超过k的最短路径的权(2<=i<=n, k>=1),可得递推公式:
d(0)(1) = 0; d(0)(i) = +∞, 2<=i<=n
d(k)(i) = min{d(k-1)(i), d(k-1)(j) + w(j, i)} | <vj, vi>∈E }, 1<=i<=n, k>=1
因为图中无负回路,所以最短路径包含边数<=n-1,所以d(n-1)(i)即为所求。
为了保存详细路径信息,用h(k)(i)保存i的下一跳,递推公式为:
h(0)(1) = 1; h(0)(i) = 0, 2<=i<=n
h(k)(i) = h(k-1)(i), 若d(k-1)(i) <= d(k-1)(j) + w(j, i)
min{j}, 若d(k-1)(i) > d(k-1)(j) + w(j, i)
Ford单源最短路径算法图例
由d(4)和h(4)可知:
v1到v2最短路径长为1, 1->2
v1到v3最短路径长为1, 1->2->5->3
v1到v4最短路径长为1, 1->4
v1到v5最短路径长为1, 1->2->5
伪代码
//初始化,k=0
d(1)←1=0, h(1)←1
for i←2 to n do
d(i)←+∞, h(i)←0
for k←1 to n-1 do
for i←1 to n do
for <vj, vi>∈E do
if d(j)+w(j,i) < d(i) then
d(i) ← d(k-1)(j)+w(j,i)
h(i) ← j
//若n-1次循环后还能更新d(i),说明到该点的最短路径还未找到,那么必定是存在负回路,返回FALSE
for i←1 to n do
for <vj, vi>∈E do
if d(j)+w(j,i) < d(i) then
return false
return d, h
算法对比
对比Floyd算法
Ford算法复杂度和Floyd算法一样为O(n^3),但Ford算法只保留单源最短路径,Floyd计算并保存多源最短路径,所以比Floyd算法节省空间,效率也较高。
在找s-t最短路径时Ford算法比Floyd算法更适合。
对比Dijkstra算法
Ford算法复杂度也可表示为O(n * m),m = |E|;相比之下,Dijkstra算法复杂度为O(n^2);当图是稀疏图时,二者相差不大。
Dijkstra算法不能处理有负回路的图,而Ford算法能