C++实现树 - 07 平衡二叉树
数据结构与算法专栏 —— C++实现
写在前面:
这一讲我们来讲讲目前为止难度最大的一种树,当然后面要有 B 树、B+ 树和红黑树等着我们。同样,我会将详细的代码附到详解的最后。
平衡二叉树的定义
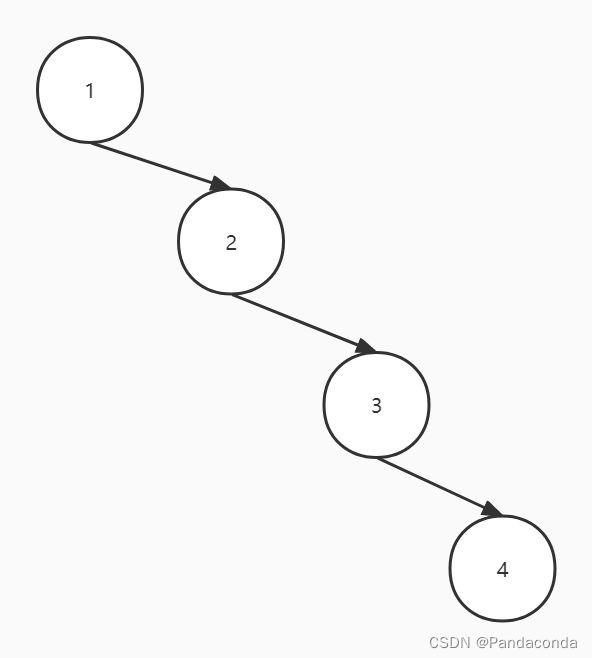
我们之前学了二叉排序树,但是二叉排序树存在一个致命的问题,如果我每次插入的值都比上一次插入的大,那它就会形成一个斜树,这对我们的查找删除等功能影响很大。
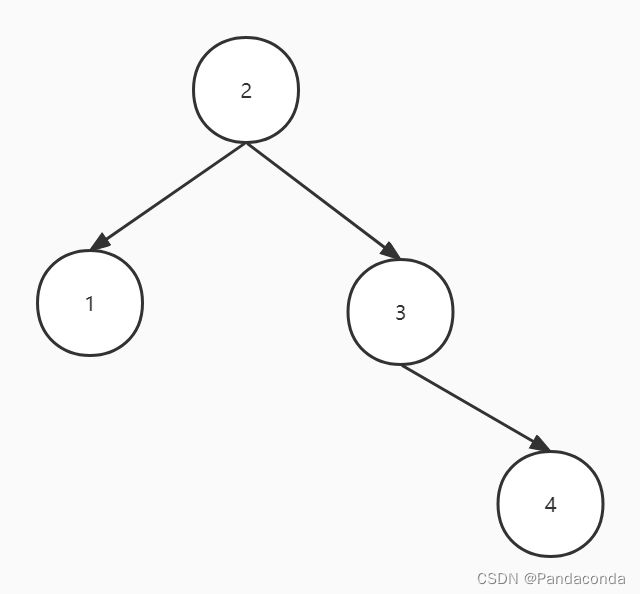
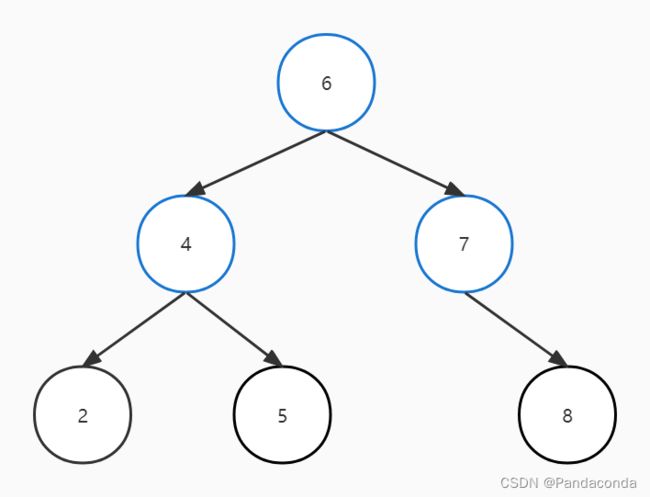
我们经过平衡操作就可以得到这样一颗树(具体如何操作下面会讲到):
所以平衡二叉树就由此诞生了,平衡二叉树定义其可以为空树,但是每个结点的左右子树的高度只差不能超过 1 ,所以就引入了一个新概念即平衡因子。而对于结点的结构体我们就要引入深度的定义。
typedef struct node {
int data; //数据
node *left; //左指针
node *right; //右指针
int height; //其左右子树最大深度
} avlnode, * avltree;
其实通过这个概念就可以发现上面那个斜树就不满足定义,同样我们多来看几个反例。
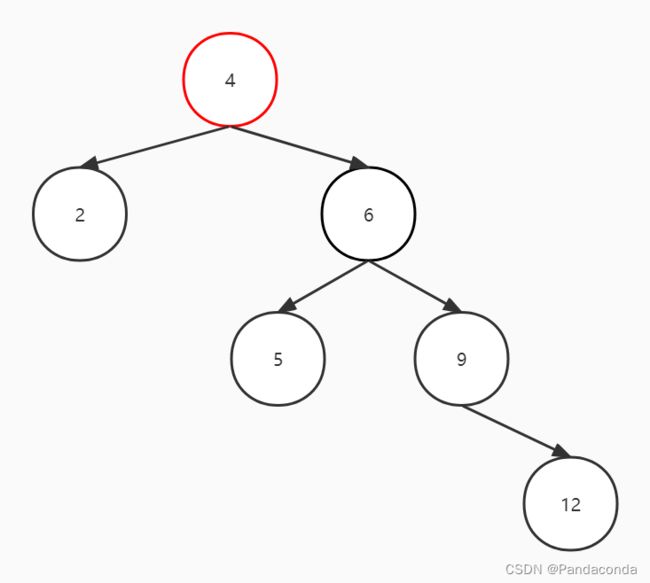
下面这棵树的结点 4 的左子树最大深度为 1 ,而右子树的最大深度为 3 ,右子树最大深度减去左子树最大深度大于 1 了,所以结点 4 就失衡了。但是我们发现,结点 6 其实并没有失衡,所以我们要做的就是对结点 4 进行平衡化操作。
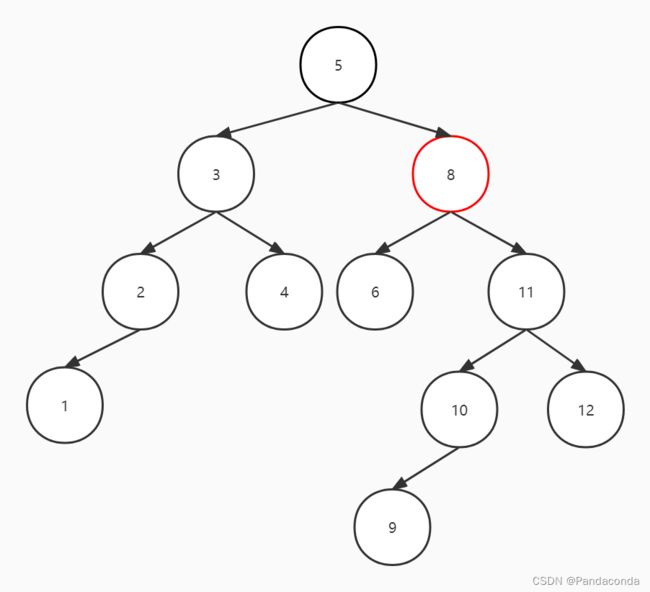
我们再来看一个比较复杂的树,可以发现这棵树中失衡的结点发生在了结点 8 ,它的左子树深度为 1 ,其右子树深度为 3 ,所以我们要对结点 8 进行平衡化操作。所以我们可以发现,并不是所有失衡结点都会发生在根结点,但是却有可能因为根结点的孩子结点进行平衡化后导致父结点失衡。
旋转操作
旋转操作应该是第一次接触平衡树时遇到的难题之一,可能会被各种左旋右旋弄得晕头转向,但这是非常正常的。俺第一次看这东西也被折磨的不轻,不过通过不懈的努力发现了其中存在的规律,下面就整理给大家。
平衡树中的旋转操作分为左旋、右旋、先左旋再右旋以及先右旋再左旋,我们先分别来看看他们是如何实现的。
此外,我们在进行旋转操作时,肯定伴随着结点深度的更新,所以我们先把获得深度的函数写出来。
//获取深度
int get_height(avlnode* node) {
//如果结点为空就返回0,如果不为空就返回它的深度
return node == NULL ? 0 : ((avlnode*)(node))->height;
}
而为了使结点的左右子树深度差不大于 1 ,就要进行旋转操作进行调整,而旋转操作就要分为四种情况,根据插入结点所在位置而定:
1、当插入结点在右孩子的右子树时,进行左旋。
2、当插入结点在左孩子的左子树时,进行右旋。
3、当插入结点在右孩子的左子树时,先进行右旋再进行左旋。
4、当插入结点在左孩子的右子树时,先进行左旋再进行右旋。
左旋
当我们往树中插入结点 3 就会发现结点 1 的右子树的深度比其左子树深度大 2 故已经失衡,这对应的是插入到右孩子的右子树的情况,要进行左旋操作。

左旋操作:
(1)将失衡结点的右孩子的左指针赋给失衡结点的右指针,即将结点 2 的左指针赋给结点 1 的右指针。
(2)然后将刚才失衡结点右孩子的左指针指向失衡结点,即将结点 2 的左指针指向结点 1 。
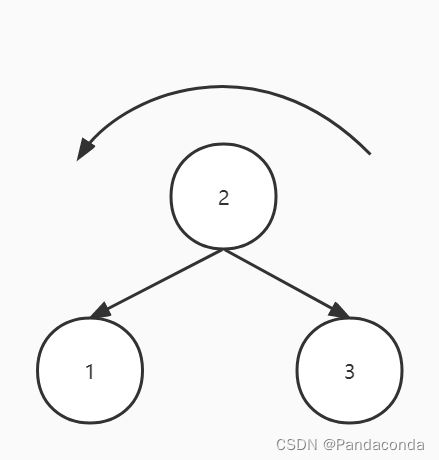
注意:每次更新完结点指针后,都要对结点的深度进行更新。
//RR 右孩子的右子树(左旋)
avltree right_right_rotation(avltree tree) {
avlnode *k = tree->right;
tree->right = k->left;
k->left = tree;
tree->height = max(get_height(tree->left), get_height(tree->right)) + 1;
k->height = max(get_height(k->left), get_height(k->right)) + 1;
return k;
}
右旋
右旋和左旋十分相似,对应的插入情况是左孩子的左子树,所以要进行右旋操作。

右旋操作:
(1)将失衡结点的左孩子的右指针赋给失衡结点的左指针,即将结点 2 的右指针赋给结点 3 的左指针。
(2)然后将刚才失衡结点左孩子的右指针指向失衡结点,即将结点 2 的右指针指向结点 3 。
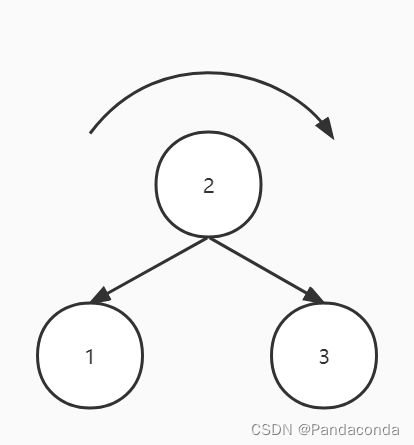
//LL 左孩子的左子树(右旋)
avltree left_left_rotation(avltree tree) {
avlnode *k = tree->left;
tree->left = k->right;
k->right = tree;
tree->height = max(get_height(tree->left), get_height(tree->right)) + 1;
k->height = max(get_height(k->left), get_height(k->right)) + 1;
return k;
}
先右旋再左旋
如果我们插入的结点在失衡结点的右孩子的左子树,就要先对失衡结点的右子树进行右旋操作,然后再对失衡结点进行左旋操作。而这里的右旋和左旋操作对应了上面讲的操作,只是对这两个操作进行了组合。
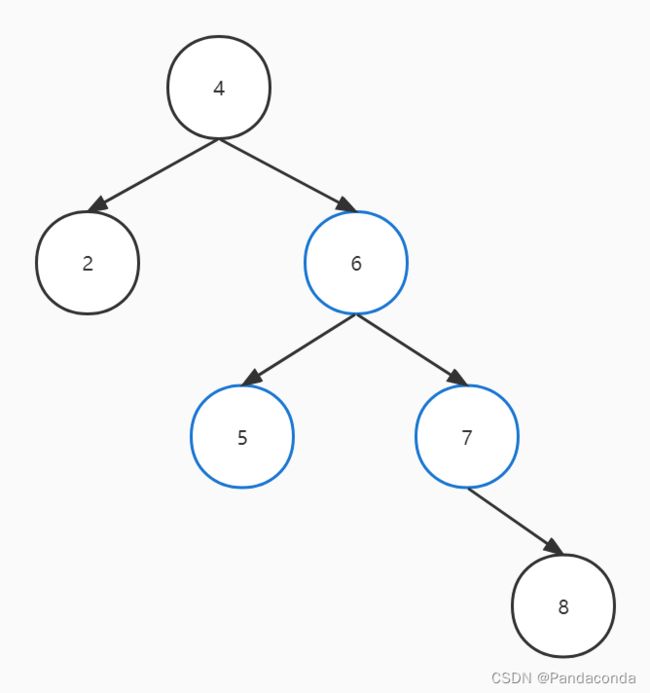
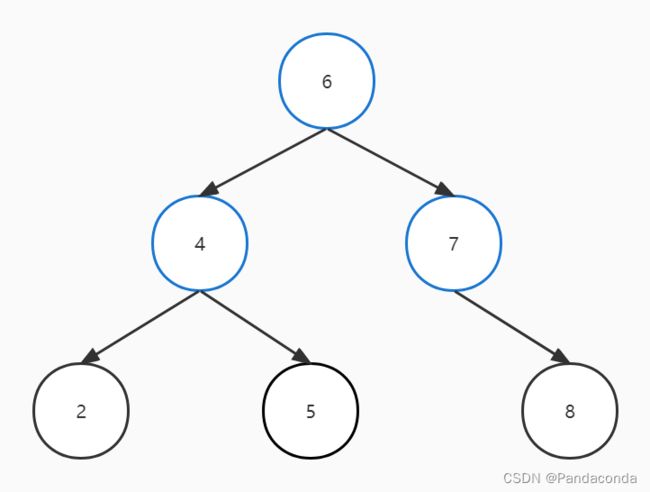
我相信很多人一开始接触这个操作肯定也有这样的疑惑,为什么不直接进行左旋操作呢,我们直接上图(注意下面的操作是错误操作):
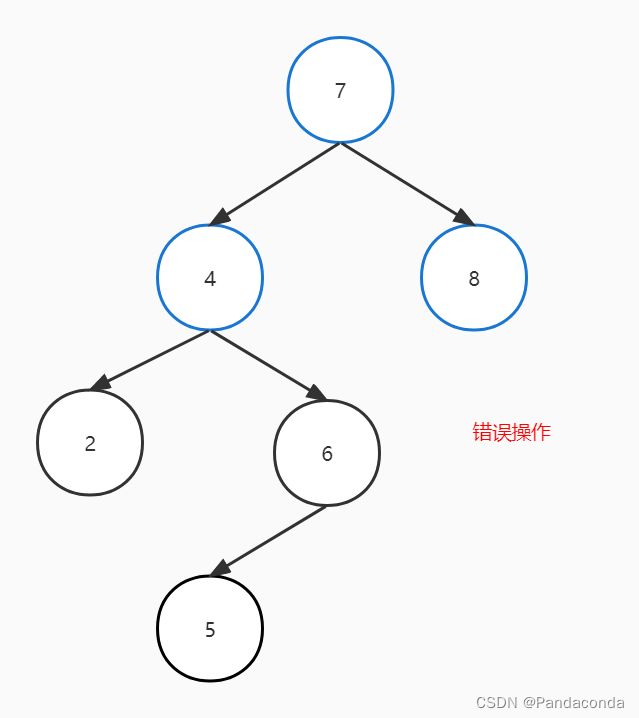
当你直接左旋之后会发现,失衡结点仍然处于失衡状态,只不过刚才是右子树深度更大,现在变成左子树深度更大罢了。所以我们要先对失衡结点的右子树进行右旋平衡化,再对失衡结点进行左旋平衡化。
//RL 右孩子的左子树(先右旋再左旋)
avltree right_left_rotation(avltree tree) {
tree->right = left_left_rotation(tree->right);
tree = right_right_rotation(tree);
return tree;
}
先左旋再右旋
这个操作与上面同理,对应着是插入结点在失衡结点左孩子的右子树的情况,所以要先对失衡结点的左孩子进行左旋操作,再对失衡结点进行右旋操作。
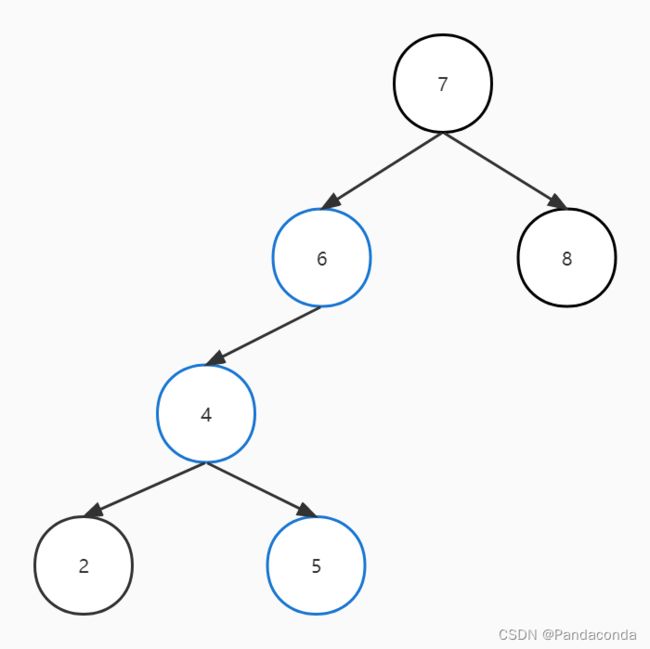
//LR 左孩子的右子树(先左旋再右旋)
avltree left_right_rotation(avltree tree) {
tree->left = right_right_rotation(tree->left);
tree = left_left_rotation(tree);
return tree;
}
插入操作
当我们熟悉完旋转操作后,就可以开始写插入操作了,我们每次插入结点后如果发现结点失衡就可以通过插入结点的情况属于上述四种中的哪一种,从而进行对应的旋转操作。
那么问题来了,我们该如何去判断插入结点后是否处于失衡状态呢。我们通过前面二叉排序树的学习可以知道,可以通过递归来找到对应的位置插入,那判断失衡状态要在哪里进行判断呢。
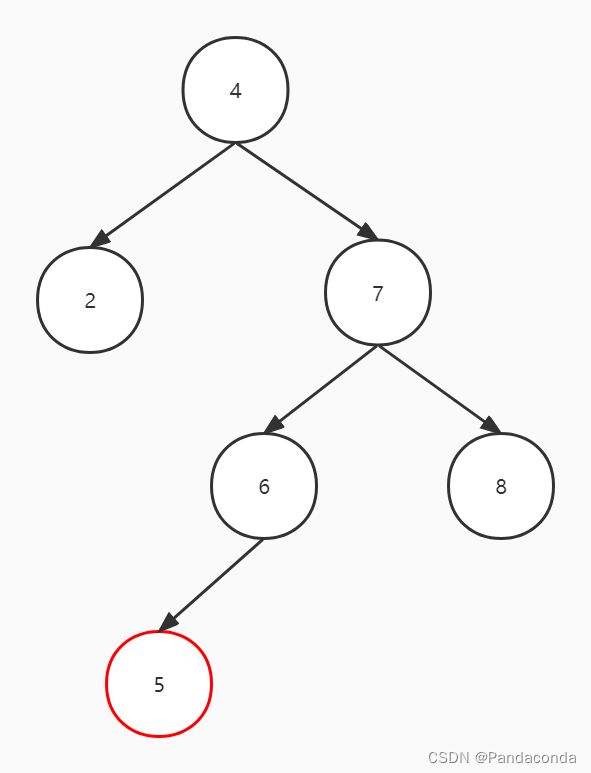
我们可以通过回溯的方法进行失衡判断,直接上图(假如我们要插入结点 5):

插入完结点后,发现结点 4 和结点 7 都处于失衡状态,这里要注意的是我们第一个要平衡化的结点是离插入结点最近的那个失衡结点,从叶子结点往上进行平衡化处理。
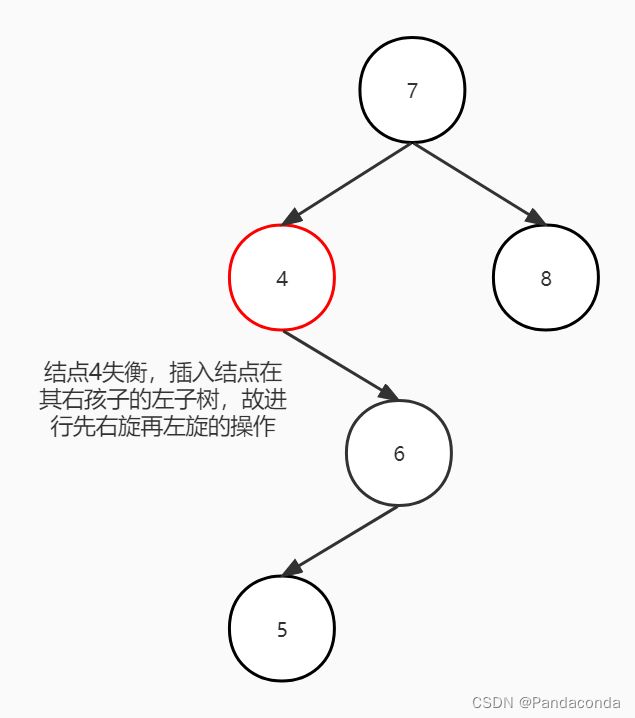

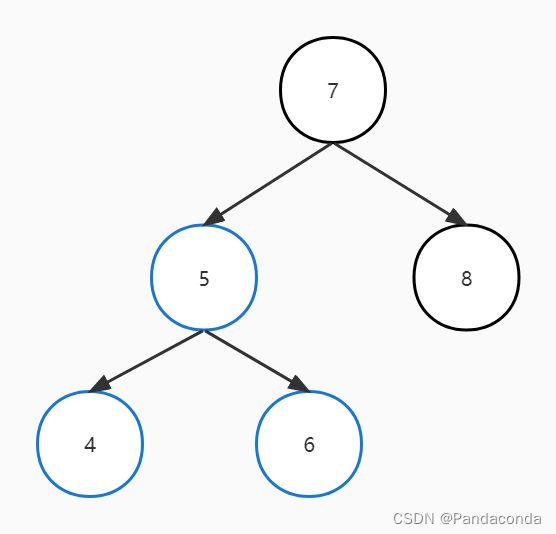
写代码的思路是先递归找到对应的位置进行插入,然后回溯判断每个结点是否失衡,如果失衡就判断失衡情况并进行对应平衡化操作。
我们每次递归时可以用结点的左右指针接收返回值,这样递归完后回溯时就可以进行失衡判断。
//插入结点
avltree avltree_insertNode(avltree tree, int key) {
//判断当前结点是否为空,如果为空则创建结点
if (tree == NULL) {
avlnode *node = creat_node(key, NULL, NULL);
tree = node;
}
//开始递归寻找插入结点的位置
else if (key < tree->data) {
tree->left = avltree_insertNode(tree->left, key); //先递归插入结点
if (get_height(tree->left) - get_height(tree->right) == 2) {
//在这里判断是LL还是LR
if (key > tree->left->data) {
tree = left_right_rotation(tree);
} else {
tree = left_left_rotation(tree);
}
}
} else if (key > tree->data) {
tree->right = avltree_insertNode(tree->right, key); //先递归插入结点
if (get_height(tree->right) - get_height(tree->left) == 2) {
//在这里判断是RL还是RR
if (key < tree->right->data) {
tree = right_left_rotation(tree);
} else {
tree = right_right_rotation(tree);
}
}
} else {
cout << "不允许插入相同的值" << endl;
}
//回溯时,更新结点深度
tree->height = max(get_height(tree->left), get_height(tree->right)) + 1;
return tree;
}
删除操作
删除操作可能要比插入操作更加复杂一些,但是总的来说还是判断结点是否失衡,只不过判断方法有所不同。因为删除结点会使删除结点所在的子树深度可能减少,如果导致结点失衡,那么旋转操作就会和插入操作相反。
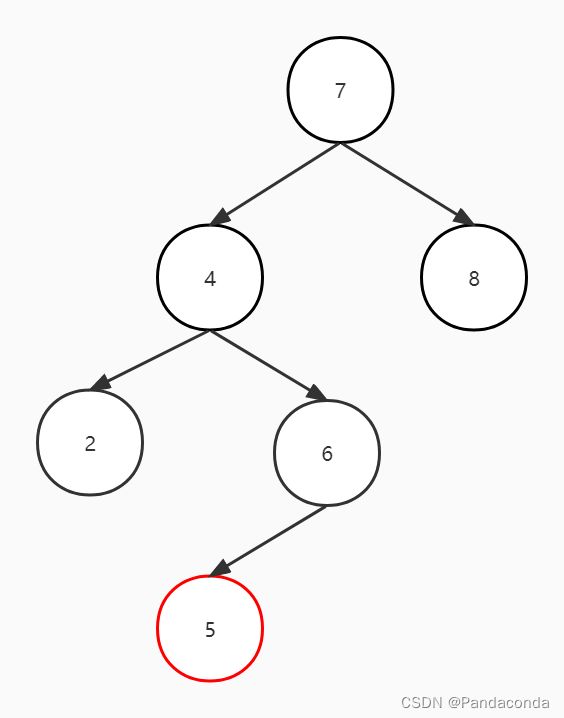
我们还是先来看看图(假如删除结点 5):
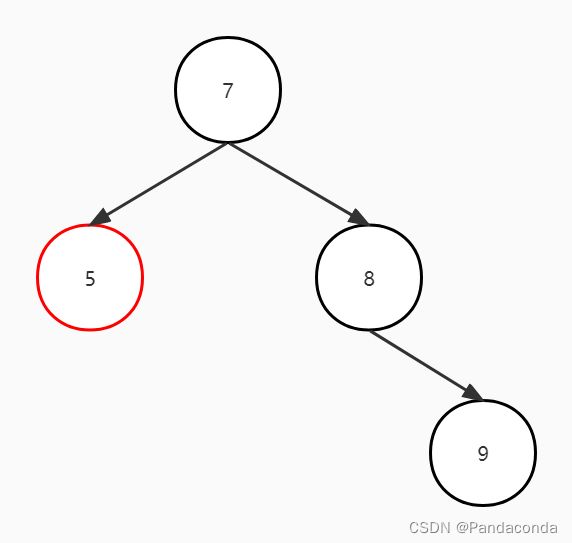
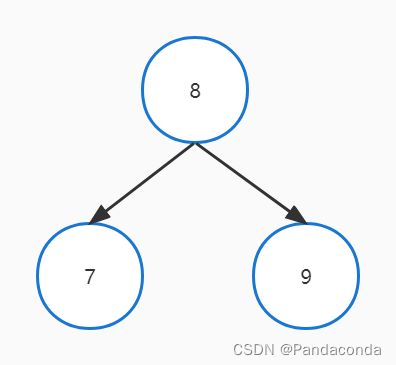
我们可以发现删除结点 5 后,结点 7 发生了失衡,因为删除的结点在结点 7 的左子树,导致右子树的深度与其左子树的深度差大于了 1 ,所以要进行左旋操作。
回顾上面插入操作,如果插入结点在失衡结点的左孩子的左子树,就要进行右旋操作,操作与删除完全相反。
所以如果删除结点在失衡结点的左子树,我们就要对失衡结点的右子树进行判断。比如上面删除结点 5 的例子,我们要对失衡结点即结点 7 进行判断,判断其右子树的左右子树谁的深度更大,其实这就和插入结点在失衡结点的右孩子的右子树还是左子树一样。
除此了平衡化操作不同之外,我们对于删除结点的操作也不同,这里我们是只在树的叶子结点进行删除,如果删除结点不是叶子结点,则就找到删除结点的前驱即左子树的最大值的这个叶子结点,将这个叶子结点的值替换到该删除结点,然后再去递归删除这个叶子结点,还是直接看图(假如要删除结点 5):
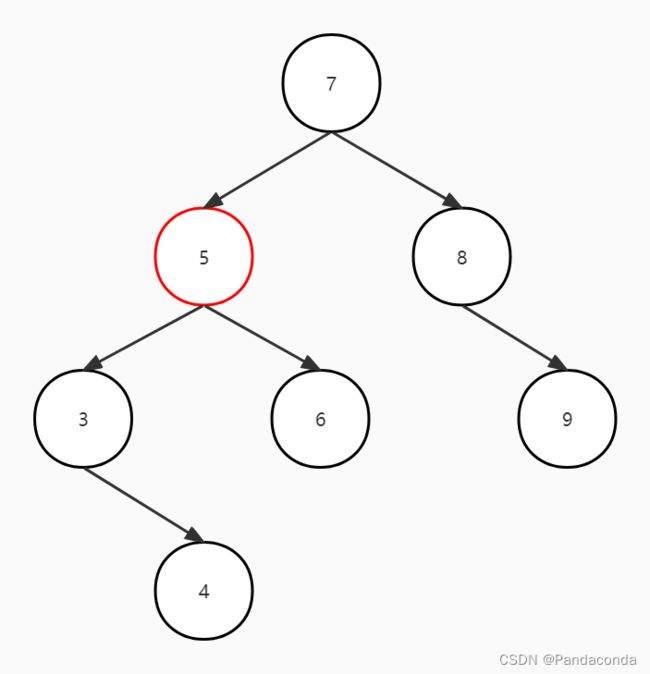
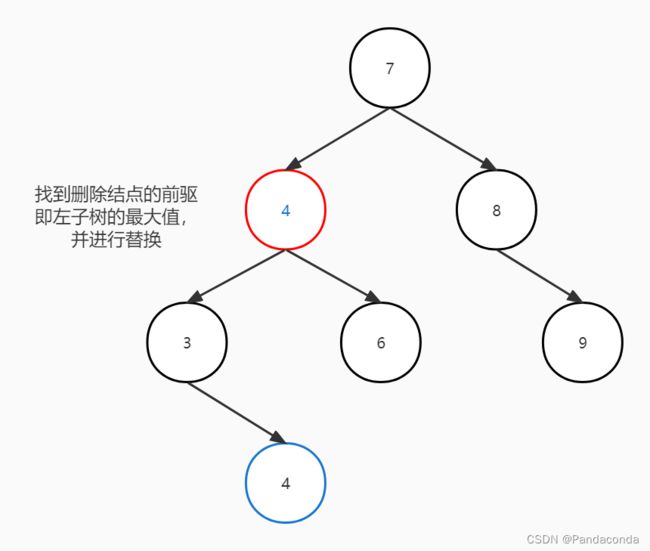
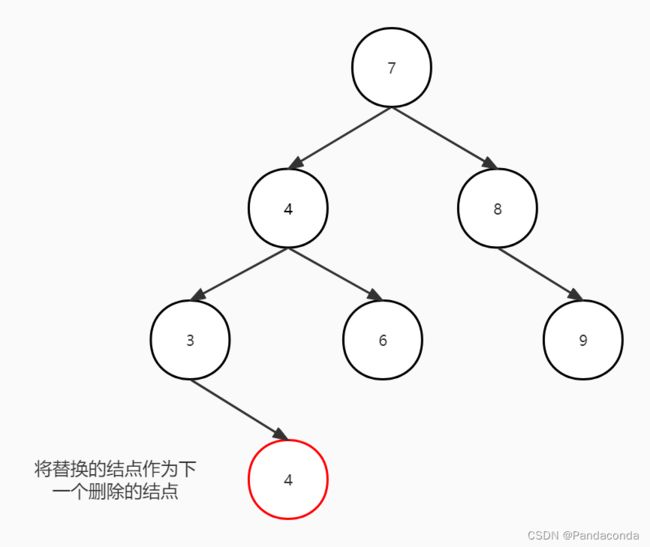

//找到删除结点的前驱(和二叉排序树类似)
avlnode *mininum_node(avltree tree) {
if (tree == NULL) {
return NULL;
}
while (tree->right) {
tree = tree->right;
}
return tree;
}
//删除结点
avltree avltree_deleNode(avltree tree, int key) {
if (tree == NULL) {
cout << "没有该结点" << endl;
return tree;
}
//要删除的结点在左子树
if (key < tree->data) {
tree->left = avltree_deleNode(tree->left, key);
//判断是否失衡
if (get_height(tree->right) - get_height(tree->left) == 2) {
int RL = get_height(tree->right->left), RR = get_height(tree->right->right);
//判断属于哪种情况
if (RL > RR) {
tree = right_left_rotation(tree);
} else {
tree = right_right_rotation(tree);
}
}
}
//要删除的结点在右子树
else if (key > tree->data) {
tree->right = avltree_deleNode(tree->right, key);
//判断是否失衡
if (get_height(tree->left) - get_height(tree->right) == 2) {
int LR = get_height(tree->left->right), LL = get_height(tree->left->left);
//判断属于哪种情况
if (LR > LL) {
tree = left_right_rotation(tree);
} else {
tree = left_left_rotation(tree);
}
}
}
//找到了要删除的结点
else {
//如果要删除的结点有两个孩子
if (tree->left && tree->right) {
//找到删除结点左子树的最大值(和二叉排序树操作类似)
avlnode *min_node = mininum_node(tree->left);
tree->data = min_node->data; //改变要删除结点的值
tree->left = avltree_deleNode(tree->left, min_node->data); //找到下一个要删除的结点
}
//如果要删除的结点只有一个孩子或者没有孩子
else {
tree = tree->left ? tree->left : tree->right;
}
}
//更新结点深度
if (tree) {
tree->height = max(get_height(tree->left), get_height(tree->right)) + 1;
}
return tree;
}
算法分析
平衡二叉树解决了二叉搜索树在斜树即遇到有序序列情况下时间复杂度到达 O(n) 的情况,使得在最坏情况下时间复杂度仍然有 O(logn)。这种优化是牺牲了插入和删除的性能换来的,所以平衡二叉树并不适用于频繁插入或删除结点的情况,后续我们要讲到的红黑树就是对平衡二叉树的进一步优化,能在搜索、插入和删除性能都不错的情况下也有个不错的速度。
全部代码
#include 如果大家有什么问题的话,欢迎在下方评论区进行讨论哦~
【上一讲】树 - 06 哈夫曼树编码
【下一讲】树 - 08 并查集