IEArch-卷积神经网络
一、感受
这次作业的神经网络是比上一次作业复杂的,上一次作业是“多层感知机(MLP)”,这一次的作业是“卷积神经网络(CNN)”。运算从原来的矩阵乘法变成了卷积,网络结构也更加复杂,所以这次的作业是允许使用框架的。
这次作业的难点本质上是对于卷积网络的理解上,TensorFlow 可以提供卷积的计算方式还有后窥修正,所需要书写的只是网络结构。次难点是 TensorFlow 的工作机理,其实一开始做的时候如果能对 TensorFlow 有一个好的理解,写起来大概 40 分钟就够了(但是学习上面这俩东西花了整整一天)。
二、卷积神经网络
2.1 卷积层
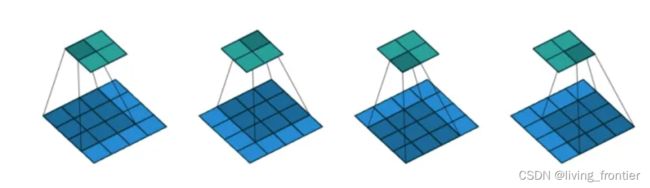
卷积运算利用一个输入矩阵和一个卷积核进行运算,卷积核会在输入矩阵上运动,然后每次都进行与输入矩阵的点对点的乘法(数学上还需要旋转卷积核 180 度,但是实现的时候不需要,因为反正也是随机的),大概如下:
关于卷积为啥要比普通的矩阵乘法(线性变化)要更加优异,我的同学说过,卷积会重复的利用输入矩阵中的信息,而且每个信息的贡献是不等的,边缘的贡献会小一些,而且卷积核这种东西本身的权重就很有灵性,而且可能有更好的数学理论支持。
如果再细说,确实感知机模型在数学上是可以完成拟合的,本质类似于用多项式模拟函数。但是这会导致训练数据集的很大,这是因为本来这件事情就是很困难的事情,但是复杂的神经网络会加入一些假设,正是由于这些假设,导致了我们可以用很小的数据集训练出很高准确率的网络。
以卷积神经网络为例,对于普通的感知机,如果想识别人脸,需要“人脸出现在图片中央,人脸出现在图片角落,人脸出现在图片次中心”等一系列数据,但是卷积神经网络就没有这个限制,卷积的计算方法会天然就可以将这些情况考虑进去。
不同的神经网络有不同的特性,对应不同的假设,如
- RNN: 时间点和时间点是相关的
- CNN: 图片相邻的像素是相关的
- Encoder-Decoder: 一个图片的信息可以压缩
- UNet: 浅层神经网络对图像边界的理解比深层神经网络好
- Dropout: 数据噪声没有意义
- 各种 attention: 图片某些位置要仔细看
- 各种 context: 图片中全局的信息很重要
不过卷积的特性就是,乘法运算的次数会大大增加(一个输入元素被算了不止一遍),所以才需要池化层和硬件加速器。
2.2 池化层
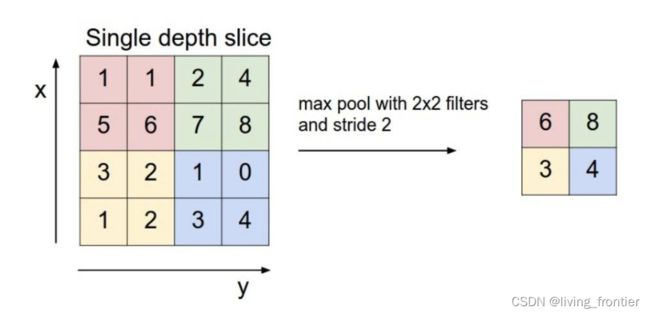
池化是为了减少卷积输入矩阵的大小而存在的,其基本原理如下:
对于一个输入矩阵,我们用一个视窗在上面移动,然后从每个视窗中用某种方法获得一个值,然后输出成输出矩阵的一个元素,上图采用的方法是在视窗中挑一个最大的元素当输出,所以叫做 max pool,常用的还有 avg pool ,是取平均值的意思。
经过池化处理,矩阵会变小,其功能有:
- 抑制噪声,降低信息冗余
- 提升模型的尺度不变性、旋转不变形
- 降低模型计算量
- 防止过拟合
需要强调的是,视窗的移动不一定不覆盖,如下图所示
2.3 其他概念
那个移动的视窗也被叫做滤波器(filter),每次移动的步幅叫做步长(stride),另外在卷积中,为了保证输入矩阵和输出矩阵的大小不发生变化(或者可控的变化),我们有在输入矩阵边缘补零(padding)的操作。正如多层感知机会有一个 b 的值在完成线性映射后,卷积神经网络也是有这样的值的,我们称之为偏置单元(bias)
三、LeNet
3.1 总论
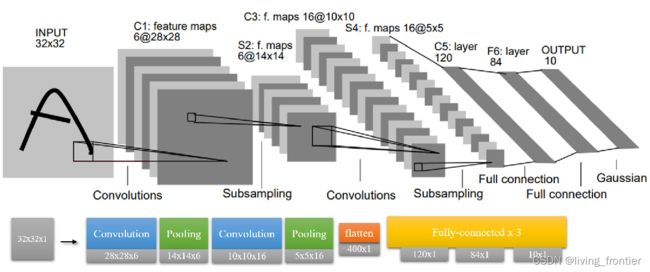
LeNet 是一个经典的卷积网络,有神经网络界的 “Hello, world” 之称,所以网上资料还是很多的。可以大量的查阅资料。
3.2 输入
虽然在经典的这张图中,一张图片的大小事 32 x 32 的,但是实际在 mnist 数据集中,一张图片的大小是 28 x 28 ,所以可以采用 padding 补零的方法让后续操作不太改变。
通过给定的输入处理函数,我们最终会获得 3 个四维的张量,分别是训练集(train),验证集(validation),测试集(test)。其四个维度为 [batch, height, width, channel] ,其中 batch 为批量之意,在这里是图片数,这里我们的训练集的 batch 为 55000, 验证集的 batch 为 5000,测试集的 batch 为 1000 ,height, width 是图片的高和宽,这里均为 28 ,channel 是通道之意,因为是黑白照片,所以 channel = 1 恒成立(如果是 RGB 彩色图片,则 channel = 3)。
3.3 Conv1
卷积层的搭建需要用到 TensorFlow 中的函数,如下示例
tf.nn.conv2d(input, filter, strides, padding)
其中 input 为输入的四维张量,很好理解。
filter 是卷积核的参数,为一个 4 维张量(不是 4 元素向量),每一维格式如下 [长,宽,输入通道数,深度] 。输入通道数应当与 input 的通道数相同,这里是 1,深度(输出通道数)自定,我们这里需要 6 张图(和上面一样,所以为 6),最终代码如下
# 5 * 5 采样窗口,6 个卷积核从 1 个平面抽取特征
conv1_w = self.init_weight([5, 5, 1, 6])
上述代码说明了我们生成了 5 x 5 的输出 6 通道的卷积核(本质应该是 6 个二维矩阵作为卷积核)。
因为最后有 6 张图,所以我们需要 6 个偏置单元
conv1_b = self.init_bias([6])
和感知器一样,我们需要选择一个激活函数,我们选择 relu ,这个的选择后面会有讨论
conv2_h = self.relu(self.conv2d(pool1_h, conv2_w), conv2_b)
其中的 self.conv2d 是这样的
def conv2d(x, W):
"""
param x: input tensor of shape [batch, in_height_, in_weight, in_channels]
param W: filter tensor of shape [filter_height, filter_width, in_channels, out_channels]
return: 一组卷积核
"""
# strides 是步长的意思,是 strides[1] 代表 x 方向的步长,strides[2] 代表 y 方向的步长
# padding 即补齐方式,SAME 不会造成输出的矩阵变小(卷积的自然情况),valid 会
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
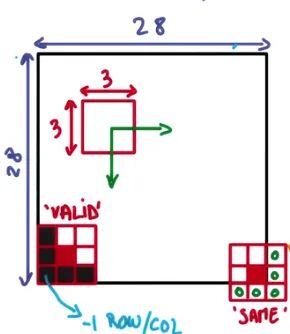
关于步长和补齐,有
其中 stride 作为一个四元数组,stride[0], stride[3] = 1 是常态,这里采用 padding = 'SAME' 的操作,就是为了适应图片是 28 x 28 的特殊性。
设输入图像尺寸为 W,卷积核尺寸为 F,步幅为 S,Padding 使用 P,则经过卷积层或池化层之后的图像尺寸为(W-F+2P)/ S + 1
- 如果参数是
SAME,那么计算只与步长有关,直接除以步长 W / S (除不尽,向上取整) - 如果参数是
VALID,那么计算公式如上:(W – F + 1) / S (结果向上取整)
经过这一层,一张图片被转换成了 6 张 28 x 28 的 feature map。
3.4 Pool1
池化层的标准都比较统一,有代码
pool1_h = self.max_pool(conv1_h)
def max_pool(x):
"""
返回一组池化核
"""
# ksize [1,x,y,1] x,y 为池化窗口大小
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
可以看到我们用到的池化层都是每 2 x 2 的窗口中取最大值,然后紧密但是无覆盖的遍历的,并且有补齐操作。这就导致经过池化层后,输入的高和宽都会变为原来的 1 2 \frac12 21 。
经过这一层,6 张 28 x 28 的 feature map 变成了 6 张 14 x 14 的 feature map。
3.5 Conv2
# 5 * 5 采样窗口,16 个卷积核从 6 个平面抽取特征
conv2_w = self.init_weight([5, 5, 6, 16])
conv2_b = self.init_bias([16])
conv2_h = self.relu(self.conv2d(pool1_h, conv2_w), conv2_b)
结构与 Conv1 类似。
经过这一层, 6 张 14 x 14 的 feature map 变成了 16 张 14 x 14 的 feature map。这里再次与官方的图发生了差异,这是因为原有代码这里肯定没有 padding,但是我 padding 了(使用了课程组提供的函数)。
3.6 Pool2
结构与 Pool1 类似
# layer 4 construct the pool2
pool2_h = self.max_pool(conv2_h)
经过这一层,16 张 14 x 14 的 feature map 变成了 16 张 7 x 7 的 feature map。
3.7 Flatten
我们需要在这里加装一个多层感知机,所以第一步是将原来的四维张量(注意,我们讨论的时候只说了后三维,第一维是图片个数,比较朴素)展成二维张量(其实本质是一维,第一维依然是图片个数),如下实例
# 第四步得到的结果拉伸为 1 个一维向量,其长度为 7 ∗ 7 ∗ 16 = 784
pool2_h_flat = tf.reshape(pool2_h, [-1, 7 * 7 * 16])
其中 reshape 的用法与 numpy 库类似,-1 代表缺省,需要根据其他维度进行计算。
经过这一层,我们得到了 784 的一维输入。
3.8 Fc1
fc1_w = self.init_weight([7 * 7 * 16, 120])
fc1_b = self.init_bias([120])
# matmul 是矩阵乘法的意思
fc1_h = self.relu(tf.matmul(pool2_h_flat, fc1_w), fc1_b)
这里用 TensorFlow 的形式重新搭建了一遍,感觉十分新奇。
经过这层,784 个输入节点转换成了 120 个隐层节点。可以说从这里开始,又与标准的 LeNet 重合了。
3.9 Fc2
与 Fc1 结构类似
fc2_w = self.init_weight([120, 84])
fc2_b = self.init_bias([84])
fc2_h = self.relu(tf.matmul(fc1_h, fc2_w), fc2_b)
经过这一层,120 个隐层节点转换成了 84 个隐层节点。
3.9 Fc3
与 Fc1 结构类似
# output layer
fc3_w = self.init_weight([84, 10])
fc3_b = self.init_bias([10])
fc3_h = tf.nn.sigmoid(tf.matmul(fc2_h, fc3_w) + fc3_b) # 输出层使用 sigmod 作为激活函数输出
这层的特殊之处在于激活函数换成了 sigmoid ,这个效果要远好于 rellu。
经过这一层,84 个隐层节点变成了 10 个输出节点。
四、TensorFlow
4.1 张量 Tensor
张量就是多维矩阵的意思,从上面的分析可知,LeNet 用 TensorFlow 实现是很恰当的。
4.2 Session 和 Computational Graph
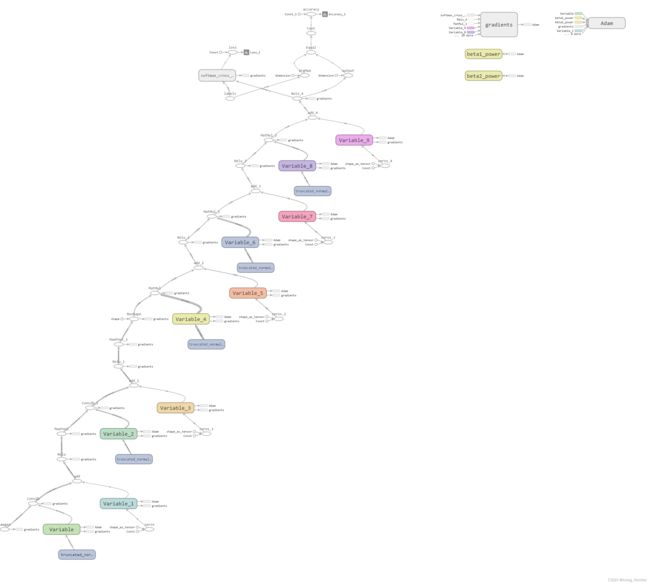
对于 TensorFlow,我们大量的运算(看似的运算),其实不是在运算,而是在写一个运算结构,比如说我们搭建的神经网络,其实上面写的东西,并没有实际运算,而是搭建成了这样的一个网络
是一个像表达式树的东西,我们需要利用“对话(session)” 来运行这个结构。
计算图包含数据(data,也就是各种Tensor)和操作(operation)。一个模型中的每一个数据或者操作都是图中的一个节点,箭头代表了数据流动的方向。上文提到的用Session计算的过程实际上就是数据流经整个图,计算出每一个节点的数值。
4.3 数据类型
4.3.1 类型需求
对于一个模型,大致有这样几种数据类型需求:
- 可更新的参数:包括权重(weights),偏置项(bias)。这些参数将在训练过程中不断更新。
- 独立于模型存在的数据:数据集中的数据需要“喂给”网络,包括输入数据、输出端的数据(输出的数据会用于反馈)。这个过程就像数学课本中给函数f(x)求值的过程,给x不同的值,求得不同的结果。可以想见,我们需要一个类似“容器”的对象,每次将数据放进去,然后计算整幅计算图。
- 常量。
- 操作符。
因此,我们有了这样的几种数据:
4.3.2 Variable
变量”是可以在程序运行过程中被改变的量,因此模型中的权重、偏置项等均使用此类型。从代码中可以看到,是这样的
@staticmethod
def init_weight(shape):
"""
Init weight parameter.
shape 是一个元组,用于描述矩阵的维度
"""
w = tf.random.truncated_normal(shape=shape, mean=0, stddev=0.1)
return tf.Variable(w)
@staticmethod
def init_bias(shape):
"""
Init bias parameter.
偏置单元(bias unit),在 y = wx + b中,b 表示函数在 y 轴上的截距,控制着函数偏离原点的距离
"""
b = tf.zeros(shape)
return tf.Variable(b)
需要注意的是,Variable 有一个初始化的过程,也就是 tf_mnist.py 中的这个代码
sess.run(tf.global_variables_initializer())
4.3.3 Placeholder
这个就是前面说的类似“容器”的对象,顾名思义,占位符就是先在模型中”占位“,至于这个位置填入的数值,在Session运行的时候再指定。我们的输入是 Placeholder
images = tf.placeholder(dtype=tf.float32, shape=[None, 28, 28, 1], name='images')
labels = tf.placeholder(dtype=tf.float32, shape=[None, 10], name='labels')
对于这种容器,我们需要在运行的时候“投喂”他,也就是这里的代码
_, loss, loss_summary = sess.run([training_operation, loss_operation, merge_summary],
feed_dict={images:batch_train_images,labels:batch_train_labels})
4.3.4 Operator
这个东西似乎包括的挺多的,一开始我模型的时候,以为没有设置前向传播和后向反馈的机制,但是后来发现不是在网络里实现的,而是在网络外部实现的,代码如下
# get loss
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(logits=out, labels=labels)
loss_operation = tf.reduce_mean(cross_entropy, name="loss")
# set up the optimizer and optimize the parameters
optimizer = tf.train.AdamOptimizer(learning_rate=lr)
training_operation = optimizer.minimize(loss_operation)
# post-processing, get accuracy
prediction = tf.argmax(out, axis=1, name='output')
correct_prediction = tf.equal(prediction, tf.argmax(labels, axis=1))
accuracy_operation = tf.reduce_mean(tf.cast(correct_prediction, tf.float32), name="accuracy")
这些运算符规定了误差的计算方式、优化器的种类,精确度的计算方式,可以说很神奇了。
五、实验结果
因为我的电脑刚装了 vitis ,导致在运行其他程序的时候经常缺失一大堆库,我努力了俩小时,到现在都没有运行起来 TensorBoard。所以可视化的图用的是同学的。
5.1 训练过程
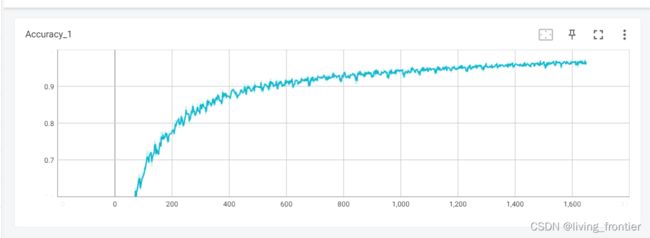
训练过程截图:
准确率变化:
loss 变化
5.2 实验结果
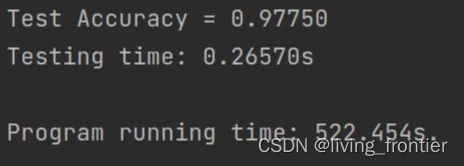
2 号实验结果截图:
不同参数数据
| 编号 | epoch | 激活函数 | 运行时间(s) | 准确率(%) |
|---|---|---|---|---|
| 1 | 100 | 最后一层为 tanh,其余为 relu | 486.825 | 98.430 |
| 2 | 100 | 最后一层为 sigmoid,其余为 relu | 522.454 | 97.750 |
| 3 | 30 | 最后一层为 sigmoid,其余为 relu | 146.511 | 96.510 |
| 4 | 30 | 均为 relu | 151.085 | 69.490 |
5.3 激活函数的选择
之所以讨论这个问题,是因为我的同学敲代码的时候将最后一层本来的 sigmoid 敲成 relu,然后导致她的正确率一直是 40% 多,最后我俩一起 de 了这个 bug,然后对激活函数的影响有了深刻认识。
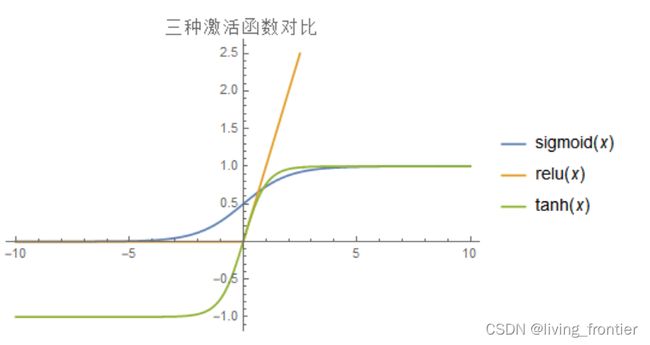
总的来说,不同的激活函数对与学习速度,过拟合现象,死神经现象都有影响,导致最终对于正确率也有一定的影响,比较详细的是和激活函数的梯度有关系,当然也和均值啥的有关系,我找到一篇写得很好的帖子,附在这里 详解激活函数 。另外并不是准确率越高越好,还要考虑训练时间、训练规模等因素。
在这个数据集和网络下,激活函数可以绘图如下
![—
title: IEArch-矩阵乘法模块
mathjax: true
tags:
- IEArch
- S5课上
- 直观理解
categories: IEArch
abbrlink: d7aec70a
date: 2022-10-26 17:43:46
一、思考题
回答 4.1.5 疑问中的疑问,
问题 1 —— 第二个矩阵计算为何出错,
问题 2 —— MAC.v 是否有修改的必要
1.1 问题 1
第一个矩阵出错的原因是在第二个矩阵计算中,在第一个矩阵中涉及到了负数
[[ 111, 25, 32, 66, -12, -99, -28, 16, -95],
[ 63, -90, -102, 40, 73, 16, -53, -33, -27],
[ -39, -79, -12, -83, -112, 59, 34, -49, -57],
[ -18, 103, -86, -51, -104, 36, -105, 112, 58],
[ 52, -12, -52, 1, -95, -123, 34, -89, 11],
[ 50, 123, 90, -74, 99, 100, 95, -12, -97],
[ 12, -94, 55, -14, 115, 84, -110, 64, 18],
[ 74, -105, -111, -43, 63, 107, 111, 56, -15]]
而在 MAC.v 代码中,对于乘法的计算,是这样的
wire signed [15:0] sf_data;
assign sf_data = $signed({8'b0, f_data});
// 本级计算
reg signed [31:0] data_reg; // 存储乘累加的结果
always @(posedge clk or posedge rst) begin
// 复位清零
if (rst) begin
data_reg <= 32'b0;
end
// 如果 valid
else if (valid) begin
// 到了最后一次计算的时候,就交给输出计算,自己复位
if (last) begin
data_reg <= 32'b0;
end
// 进行一个乘累加操作
else begin
data_reg <= data_reg + $signed(w_data) * $signed(sf_data);
end
end
// 保持原值不变
else begin
data_reg <= data_reg;
end
end
因为 8 位的操作数乘法运算,可能出现 16 位的结果,而零拓展只适用于无符号乘法,而第二个矩阵中出现的第一个矩阵中出现了负数,这就导致了运算错误的出现。只需要将其修改如下
assign sf_data = $signed( {{8{f_data[7]}}, f_data}); // 修改后
assign sf_data = $signed({8'b0, f_data}); // 修改前
那么就可以有 test.py 中的输出结果,如图所示
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CkrBahaL-1680742585745)(IEArch-矩阵乘法模块/image-20221026185805539.png)]
1.1 问题 2
没有必要修改,因为根据题义描述,这个模块将被用于全连接层,其输入格式是
feature 是 uint8,weight 是 int8
全连接层的计算方式为 F ⋅ W F \cdot W F⋅W 。从上面的分析可以看出,这个模块未修改前对于 W W W 中的负数分量就可以正确处理,只是没有办法处理 F F F 中的负数分量,但是由输入格式可知, F F F 的分量是 uint8,其范围是 0 ~ 255 所以不会出现负数情况,所以是没有必要修改的。
二、矩阵乘模块设计文档
2.1 设计功能
对于 Multiply_8x8 模块,它接受一个 8 x num 的分量为 uint8 的 F e a t u r e Feature Feature 矩阵和一个 num x 8 的分量为 int 的 W e i g h t Weight Weight 矩阵,在经过一定的周期后输出 F e a t u r e ⋅ W e i g h t Feature \cdot Weight Feature⋅Weight 。
对于 MAC 模块,它将输入的 uint8 的值和 int8 的值相乘,并与保存在寄存器中的值进行加和,然后将结果继续保存在这个寄存器中。除了计算功能以外,MAC 还有传递输入数据和传递计算结果的功能。
2.2 接口说明
对于 Multiply_8x8 模块有
| 名称 | 位宽 | 符号 | 方向 | 含义 |
|---|---|---|---|---|
| clk | 1 | unsigned | input | 时钟信号 |
| rst | 1 | unsigned | input | 复位信号 |
| fvalid0 | 1 | unsigned | input | F F F 矩阵的第 0 行输入是否有效 |
| fdata0 | 8 | unsigned | input | F F F 矩阵的第 0 行输入数据 |
| fvalid1 | 1 | unsigned | input | F F F 矩阵的第 1 行输入是否有效 |
| fdata1 | 8 | unsigned | input | F F F 矩阵的第 1 行输入数据 |
| fvalid2 | 1 | unsigned | input | F F F 矩阵的第 2 行输入是否有效 |
| fdata2 | 8 | unsigned | input | F F F 矩阵的第 2 行输入数据 |
| fvalid3 | 1 | unsigned | input | F F F 矩阵的第 3 行输入是否有效 |
| fdata3 | 8 | unsigned | input | F F F 矩阵的第 3 行输入数据 |
| fvalid4 | 1 | unsigned | input | F F F 矩阵的第 4 行输入是否有效 |
| fdata4 | 8 | unsigned | input | F F F 矩阵的第 4 行输入数据 |
| fvalid5 | 1 | unsigned | input | F F F 矩阵的第 5 行输入是否有效 |
| fdata5 | 8 | unsigned | input | F F F 矩阵的第 5 行输入数据 |
| fvalid6 | 1 | unsigned | input | F F F 矩阵的第 6 行输入是否有效 |
| fdata6 | 8 | unsigned | input | F F F 矩阵的第 6 行输入数据 |
| fvalid7 | 1 | unsigned | input | F F F 矩阵的第 7 行输入是否有效 |
| fdata7 | 8 | unsigned | input | F F F 矩阵的第 7 行输入数据 |
| wvalid0 | 1 | unsigned | input | W W W 矩阵的第 0 列输入是否有效 |
| wdata0 | 8 | signed | input | W W W 矩阵的第 0 列输入数据 |
| wvalid1 | 1 | unsigned | input | W W W 矩阵的第 1 列输入是否有效 |
| wdata1 | 8 | signed | input | W W W 矩阵的第 1 列输入数据 |
| wvalid2 | 1 | unsigned | input | W W W 矩阵的第 2 列输入是否有效 |
| wdata2 | 8 | signed | input | W W W 矩阵的第 2 列输入数据 |
| wvalid3 | 1 | unsigned | input | W W W 矩阵的第 3 列输入是否有效 |
| wdata3 | 8 | signed | input | W W W 矩阵的第 3 列输入数据 |
| wvalid4 | 1 | unsigned | input | W W W 矩阵的第 4 列输入是否有效 |
| wdata4 | 8 | signed | input | W W W 矩阵的第 4 列输入数据 |
| wvalid5 | 1 | unsigned | input | W W W 矩阵的第 5 列输入是否有效 |
| wdata5 | 8 | signed | input | W W W 矩阵的第 5 列输入数据 |
| wvalid6 | 1 | unsigned | input | W W W 矩阵的第 6 列输入是否有效 |
| wdata6 | 8 | signed | input | W W W 矩阵的第 6 列输入数据 |
| wvalid7 | 1 | unsigned | input | W W W 矩阵的第 7 列输入是否有效 |
| wdata7 | 8 | signed | input | W W W 矩阵的第 7 列输入数据 |
| num_valid_ori | 1 | unsigned | input | W W W 矩阵的列数(同时也是 F F F 的行数)是否有效 |
| num_ori | 32 | unsigned | input | W W W 矩阵的列数(同时也是 F F F 的行数) |
| valid_o0 | 1 | unsigned | output | 结果矩阵的第 0 行是否有效 |
| data_o0 | 32 | signed | output | 结果矩阵的第 0 行输出数据 |
| valid_o1 | 1 | unsigned | output | 结果矩阵的第 1 行是否有效 |
| data_o1 | 32 | signed | output | 结果矩阵的第 1 行输出数据 |
| valid_o2 | 1 | unsigned | output | 结果矩阵的第 2 行是否有效 |
| data_o2 | 32 | signed | output | 结果矩阵的第 2 行输出数据 |
| valid_o3 | 1 | unsigned | output | 结果矩阵的第 3 行是否有效 |
| data_o3 | 32 | signed | output | 结果矩阵的第 3 行输出数据 |
| valid_o4 | 1 | unsigned | output | 结果矩阵的第 4 行是否有效 |
| data_o4 | 32 | signed | output | 结果矩阵的第 4 行输出数据 |
| valid_o5 | 1 | unsigned | output | 结果矩阵的第 5 行是否有效 |
| data_o5 | 32 | signed | output | 结果矩阵的第 5 行输出数据 |
| valid_o6 | 1 | unsigned | output | 结果矩阵的第 6 行是否有效 |
| data_o6 | 32 | signed | output | 结果矩阵的第 6 行输出数据 |
| valid_o7 | 1 | unsigned | output | 结果矩阵的第 7 行是否有效 |
| data_o7 | 32 | signed | output | 结果矩阵的第 7 行输出数据 |
对于 MAC 模块,有
| 名称 | 位宽 | 符号 | 方向 | 含义 |
|---|---|---|---|---|
| clk | 1 | unsigned | input | 时钟信号 |
| rst | 1 | unsigned | input | 复位信号 |
| num_valid | 1 | unsigned | input | 乘累加长度 num 是否有效 |
| num | 32 | unsigned | input | 乘累加长度 |
| num_r_valid | 1 | unsigned | output | 传播到下一 MAC 的乘累加长度是否有效 |
| num_r | 32 | unsigned | output | 传播到下一 MAC 的乘累加长度 |
| w_valid | 1 | unsigned | input | W W W 矩阵的一个分量是否有效 |
| w | 8 | signed | input | W W W 矩阵的一个分量 |
| w_r_valid | 1 | unsigned | output | 传播到下一 MAC 的 W W W 矩阵的一个分量是否有效 |
| w_r | 8 | signed | output | 传播到下一 MAC 的 W W W 矩阵的一个分量长度 |
| f_valid | 1 | unsigned | input | F F F 矩阵的一个分量是否有效 |
| f | 8 | unsigned | input | F F F 矩阵的一个分量 |
| f_r_valid | 1 | unsigned | output | 传播到下一 MAC 的 F F F 矩阵的一个分量是否有效 |
| f_r | 8 | unsigned | output | 传播到下一 MAC 的 F F F 矩阵的一个分量长度 |
| valid_l | 1 | unsigned | input | 下一个 MAC 的运算结果是否有效 |
| data_l | 32 | signed | input | 下一个 MAC 的运算结果 |
| valid_o | 1 | unsigned | output | 该 MAC 的运算结果是否有效 |
| data_o | 32 | signed | output | 该 MAC 的运算结果 |
2.3 设计思想及流程描述
为了更好的展示设计思想和流程,这里采用一个简化版的矩阵乘法,比较方便描述。
流程主要分为两个部分,一个是计算,一个是将结果传出。
2.3.1 简单流程模拟
我们规定我们的需求是计算
F 2 × 3 ⋅ W 3 × 2 = R 2 × 2 F_{2 \times 3} \cdot W_{3 \times 2} = R_{2\times 2} F2×3⋅W3×2=R2×2
其中有
F = [ 1 2 3 4 5 6 ] W = [ 7 8 9 10 11 12 ] F = \left[ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix} \right] \quad\quad W = \left[ \begin{matrix} 7 & 8 \\ 9 & 10\\ 11 & 12 \end{matrix} \right] F=[142536]W= 791181012
此时我们只需要一个 2 x 2 个 MAC 即可完成运算,如下所示
Cycle 0
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OS7CAubt-1680742585746)(IEArch-矩阵乘法模块/cycle0.png)]
首先数据呈现这这种形式
Cycle 1
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AdOK3CB2-1680742585747)(IEArch-矩阵乘法模块/cycle1.png)]
Cycle 2
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hjSiySQl-1680742585748)(IEArch-矩阵乘法模块/cycle2.png)]
Cycle 3
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0aVUAUn0-1680742585749)(IEArch-矩阵乘法模块/cycle3.png)]
Cycle 4
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hxd9caP7-1680742585751)(IEArch-矩阵乘法模块/cycle4.png)]
Cycle 5
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OtpgP2XD-1680742585752)(IEArch-矩阵乘法模块/cycle5.png)]
Cycle 6
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6c2nYN77-1680742585753)(IEArch-矩阵乘法模块/cycle6.png)]
对于这样的一个计算,需要花
2 + 3 + 2 = 7 2 + 3 + 2 = 7 2+3+2=7
个周期就可以得到结果。
2.3.2 设计思想
对于矩阵乘法,可以看做是一堆数进行有规律、有复用的乘加运算,所以搭建模块解决这个问题,需要将其按照规律一步一步的进行计算。普世分析
A p × n ⋅ B n × q = R p × q A_{p \times n} \cdot B_{n \times q} = R_{p \times q} Ap×n⋅Bn×q=Rp×q
对于 MAC 模块,它对应这结果矩阵 R R R 中的一个分量,为了计算这个分量,需要进行 n 次的乘并累加操作。所以一般是在 n 个周期内完成的。需要注意的是,对于 A , B A, B A,B 中的某个分量,不止会被一个 MAC 利用,所以 MAC 还承担着传播分量的作用,除此之外,MAC 计算出结果后,还需要将结果通过 MAC 网络传递出去。
那么又没有什么更快的改进方法呢,其实是有的,比如说下面这种方法,就可以缩短传入的时间
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-p9fatBYt-1680742585754)(IEArch-矩阵乘法模块/微信图片_20221026212853.jpg)]
但是要付出更多的布线还有驱动的代价,所以综合考虑,还是利用了第一种。
2.4 内部关键信号与变量描述
在 MAC 中,固定长度的累加操作,是通过一个计数器 num_cnt 实现的,如下所示
// 本级控制信号
reg [31:0] num_cnt; // 已经计算的轮数
wire valid = w_valid & f_valid; // 输入数据是否有效
wire last = (num_cnt == num_r - 1'b1); // 是否是最后一次计算
// num_cnt 用于计数
always @(posedge clk or posedge rst) begin
// 复位
if (rst) begin
num_cnt <= 32'b0;
end
// 当 valid 信号有效时,num_cnt 会发生变化
else if (valid) begin
// 应该是 cnt 增加到一定的值(num_r)以后,就会重新开始
if (last) begin
num_cnt <= 32'b0;
end
// num_cnt 递增
else begin
num_cnt <= num_cnt + 1'b1;
end
end
// valid 信号无效,则保持原值
else begin
num_cnt <= num_cnt;
end
end
MAC 不仅需要传输自己的运算结果,而且需要传输其下面的 MAC 传输的结果,是通过一个 MUX 实现的,如下所示
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FXoxkOrh-1680742585755)(IEArch-矩阵乘法模块/image-20221026213308193.png)]
这个结构的对应代码如下
// 数据输出,纵向向上传播
always @(posedge clk or posedge rst) begin
if (rst) begin
data_o <= 32'b0;
end
// 最后一次的计算在这里进行
else if (valid & last) begin
data_o <= data_reg + $signed(w_data) * $signed(sf_data);
end
// 数据被更新成一个外来值
else if (valid_l) begin
data_o <= data_l;
end
// 保持原值
else begin
data_o <= data_o;
end
end
// valid_o 是一个输出项,当 data_o 有效的时候,他就是有效的
always @(posedge clk or posedge rst) begin
if (rst) begin
valid_o <= 32'b0;
end
else begin
valid_o <= (valid & last) | valid_l;
end
end
可以看到当输出数据有两个来源,一个是本身计算的数据 data_reg 一个是其下的 MAC 的计算数据 data_l 。而且 data_l 的优先级更高,这是因为当下方数据有效时,当前 MAC 一定已经计算出来了。
在 Multiply_8x8 中,这个模块控制了数据的流向,比如说纵向传播,写法是这样的
assign w_valid[0] = wvalid0;
assign w_valid[1] = wvalid1;
assign w_valid[2] = wvalid2;
assign w_valid[3] = wvalid3;
assign w_valid[4] = wvalid4;
assign w_valid[5] = wvalid5;
assign w_valid[6] = wvalid6;
assign w_valid[7] = wvalid7;
assign w_valid[8] = w_valid_r[0];
assign w_valid[9] = w_valid_r[1];
assign w_valid[10] = w_valid_r[2];
assign w_valid[11] = w_valid_r[3];
assign w_valid[12] = w_valid_r[4];
assign w_valid[13] = w_valid_r[5];
assign w_valid[14] = w_valid_r[6];
assign w_valid[15] = w_valid_r[7];
assign w_valid[16] = w_valid_r[8];
assign w_valid[17] = w_valid_r[9];
assign w_valid[18] = w_valid_r[10];
assign w_valid[19] = w_valid_r[11];
assign w_valid[20] = w_valid_r[12];
assign w_valid[21] = w_valid_r[13];
assign w_valid[22] = w_valid_r[14];
assign w_valid[23] = w_valid_r[15];
assign w_valid[24] = w_valid_r[16];
assign w_valid[25] = w_valid_r[17];
assign w_valid[26] = w_valid_r[18];
assign w_valid[27] = w_valid_r[19];
assign w_valid[28] = w_valid_r[20];
assign w_valid[29] = w_valid_r[21];
assign w_valid[30] = w_valid_r[22];
assign w_valid[31] = w_valid_r[23];
assign w_valid[32] = w_valid_r[24];
assign w_valid[33] = w_valid_r[25];
assign w_valid[34] = w_valid_r[26];
assign w_valid[35] = w_valid_r[27];
assign w_valid[36] = w_valid_r[28];
assign w_valid[37] = w_valid_r[29];
assign w_valid[38] = w_valid_r[30];
assign w_valid[39] = w_valid_r[31];
assign w_valid[40] = w_valid_r[32];
assign w_valid[41] = w_valid_r[33];
assign w_valid[42] = w_valid_r[34];
assign w_valid[43] = w_valid_r[35];
assign w_valid[44] = w_valid_r[36];
assign w_valid[45] = w_valid_r[37];
assign w_valid[46] = w_valid_r[38];
assign w_valid[47] = w_valid_r[39];
assign w_valid[48] = w_valid_r[40];
assign w_valid[49] = w_valid_r[41];
assign w_valid[50] = w_valid_r[42];
assign w_valid[51] = w_valid_r[43];
assign w_valid[52] = w_valid_r[44];
assign w_valid[53] = w_valid_r[45];
assign w_valid[54] = w_valid_r[46];
assign w_valid[55] = w_valid_r[47];
assign w_valid[56] = w_valid_r[48];
assign w_valid[57] = w_valid_r[49];
assign w_valid[58] = w_valid_r[50];
assign w_valid[59] = w_valid_r[51];
assign w_valid[60] = w_valid_r[52];
assign w_valid[61] = w_valid_r[53];
assign w_valid[62] = w_valid_r[54];
assign w_valid[63] = w_valid_r[55];
其中比较关键的变量还有 num 表示计算的次数。](https://img-blog.csdnimg.cn/7f4f7c8d8e5d4f8c9551b5c962693bd7.png#pic_center)