【论文笔记·RL】Traffic Signal Control Based on Reinforcement Learning with Graph Convolutional Neural Nets
Traffic Signal Control Based on Reinforcement Learning with Graph Convolutional Neural Nets
摘要
之前的强化学习方法都是用的是标准的神经网络,如卷积神经网络,来处理高维特征空间。而但对于多个交叉路口的交通网络,需要手动创建道路间的几何特征。文章采用了图卷积神经网络GCNN,通过多个神经网络层的叠加,自动提取距离较远的道路交通特征。在六路口环境中对所提出的方法进行了评估。研究结果表明,该方法能够以2倍于常规神经网络RL方法的速度找到可比策略,并能适应更广泛的交通需求变化。
介绍
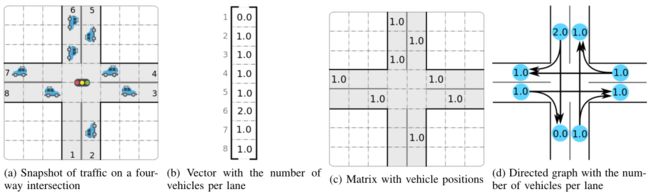
上图(a)中展示了一个四向交叉口的交通快照。图(b)-(d)显示了交通的典型特征表示。
文章使用神经网络拟合Q-Learning的迭代过程(NFQI),每个agent可以利用周边道路的交通信息学习一种策略,以分布式方式控制十字路口的交通信号。采用sumo进行模拟仿真,仿真结果表明,该方法能够以两倍于基于强化学习的全连接神经网络(FCNN)方法的速度找到可比策略,并能处理更广泛的交通需求变化。
本文贡献如下:
- 利用GCNN设计了一种基于强化学习方法的交通信号控制算法,GCNN能够自动提取具有多个交叉路口的路网中外围道路的交通特征;
- agent能够进行分布式实现,并且采取文章所提方法学习策略;
- 所提方法相较于基于FCNN的传统强化学习方法快两倍。
基础
马尔科夫决策过程
k k k步NFQI
研究表明多步方法计算TD误差可减少学习方差。
GCNN
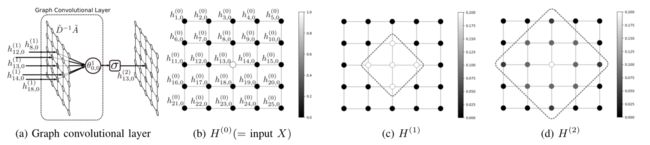
GCNN由GC层堆叠而成,文章采用Schlichtkrull等人提出的GCNN方法。本文中图 G = ( N , E ) G=(N,E) G=(N,E),其中 N N N维顶点集合, E E E为边集合。第 l + 1 l+1 l+1层的输出 H ( l + 1 ) H^{(l+1)} H(l+1)使用第 l l l层的输出 H ( l ) H^{(l)} H(l)在有向图中进行计算:
H ( l + 1 ) = σ ( D ~ − 1 A ~ H ( l ) θ ( l ) ) H^{(l+1)}=\sigma(\tilde{D}^{-1}\tilde{A}H^{(l)}\theta^{(l)}) H(l+1)=σ(D~−1A~H(l)θ(l))
- A ~ : = A + I \tilde{A}:=A+I A~:=A+I
- D ~ : = D + I \tilde{D}:=D+I D~:=D+I
- H ( l ) H^{(l)} H(l)是第 l l l层的输出,其中当 l = 0 l=0 l=0时, H ( 0 ) = x ∈ R N × C H^{(0)}=x\in \mathbb{R}^{N\times C} H(0)=x∈RN×C
由上图可知,GCNN相较于FCNN,GCNN可以通过不断的堆叠来连接到相邻单元,这样可以有效减少连接数以及参数数量。
基于强化学习的GCNN交通信号控制方法
成本函数(对应奖励函数)
交通信号控制的目标是尽量减少相对于所有车辆的总行驶时间,但总行驶时间不能被使用来进行时间步上的计算,故使用所有车辆的总等待时间作为成本函数 r r r。
r i , t : = ∑ j ∈ V i w j , t w j , t : = { 0 , v j , t > 0.1 w j , t − 1 + Δ t , o t h e r w i s e r_{i,t}:=\sum_{j\in V_i}w_{j,t}\\ w_{j,t}:=\begin{cases} 0,& v_{j,t}>0.1\\ w_{j,t-1}+\Delta t,&otherwise \end{cases} ri,t:=j∈Vi∑wj,twj,t:={0,wj,t−1+Δt,vj,t>0.1otherwise
i i i是交叉路口序号, V i V_i Vi代表交叉路口 i i i的机动车集合, w j , t w_{j,t} wj,t代表时间 t t t机动车 j j j的等待时间, v j , t v_{j,t} vj,t代表时间 t t t机动车 j j j的速度。则交叉路口 i i i的Q值可计算为:
Q i ( s t , a ) = r i , t + E s t + 1 ∼ p ( s t + 1 ∣ s t , a ) [ γ V i ( s t + 1 ) ] Q_i(s_t,a)=r_{i,t}+\mathbb{E}_{s_{t+1}\sim p(s_{t+1}|s_t,a)}[\gamma V_i(s_{t+1})] Qi(st,a)=ri,t+Est+1∼p(st+1∣st,a)[γVi(st+1)]
状态与动作表示
文章使用了两个特征:车队长度、平均速度。状态使用 2 N 2N 2N维特征向量表示,其中 N N N是车道数。
GCNN的函数逼近及拟合
实验
文章对比了NFQI with GCNN(文章所提方法)、固定时间算法、NFQI with FCNN。
模拟设置
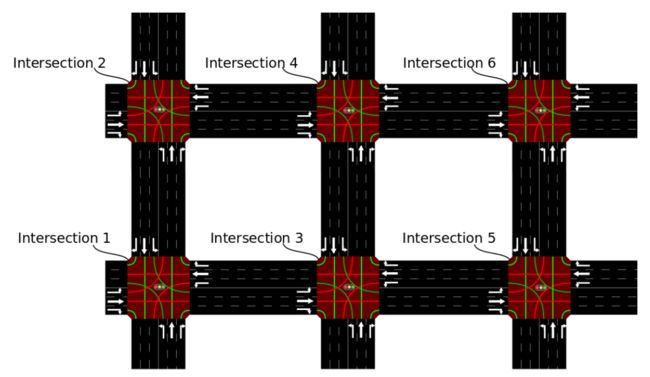
使用sumo进行模拟,采用6个交叉路口,每个交叉路口4条六车道道路,每条道路400m长,限速50km/h,车辆长度5m,车辆最小间距2.5m。生成了500s的交通轨迹。
车辆生成速率为0.5,即在路网中每秒产生0.5辆车辆,用于学习,车辆生成速率为0.25至4.0辆/秒用于评估。此外,每辆车从一组最短路径中随机选择一条路线前往指定的目的地。
上表为文章的相位设置。
神经网络结构
文章采用了一种嗲用GCL的神经网络和竞争网络结构。竞争网络结构通过将状态动作价值函数 Q ( s , a ) Q(s,a) Q(s,a)分解为状态价值函数 V ( s ) V(s) V(s)和优势函数 A ( s , a ) A(s,a) A(s,a):
Q ^ ( s , a ; θ ) = V ^ ( s ; θ ) + ( A ^ ( s , a ; θ ) − 1 ∣ A ∣ ∑ a ∈ A A ^ ( s , a ; θ ) ) \hat{Q}(s,a;\theta)=\hat{V}(s;\theta)+(\hat{A}(s,a;\theta)-\frac{1}{|\mathcal{A}|}\sum_{a\in \mathcal{A}}\hat{A}(s,a;\theta)) Q^(s,a;θ)=V^(s;θ)+(A^(s,a;θ)−∣A∣1a∈A∑A^(s,a;θ))
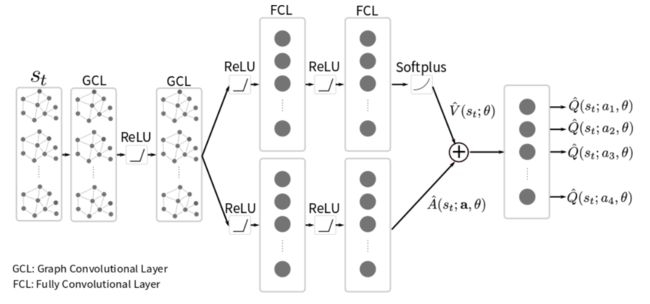
上图展示了用于交通信号控制的神经网络结构。输入层有102个单元(即17条道路×6车道)。第二层和第三层设置为gcl,共102个单元。第4层和第5层分叉,第4层和第5层是fcl,分别有51个和25个单元,以隐式方式近似 V ( s ; θ ) V(s;\theta) V(s;θ)和 A ( s , a ; θ ) A(s,a;\theta) A(s,a;θ)。第5层的输出 V ^ \hat{V} V^和 A ^ \hat{A} A^的大小为1和4,第6层的输出 Q ^ \hat{Q} Q^为4,与信号相位保持一致。Softplus函数和ReLu被作为第五层输出和其他层输出的激活函数。
在与FCNN进行比较时,GCNN中所有的GCL层都被替换为FCL层。
训练集和评价指标
文章使用固定时间交通信号控制的交通数据,收集得到适当的真实数据,共1200条轨迹,其中车辆生成率为0.5,即在道路端点随机均匀生成0.5辆车辆。每条车道都需要500秒的模拟。
评价指标采用了每个交叉路口 i i i所有机动车和时间步的平均等待时间 W ˉ i \bar{W}_i Wˉi、所有交叉路口平均等待时间的平均等待时间 W ˉ \bar{W} Wˉ。这两个指标的平均值试验次数为 M = 20 M=20 M=20。
W ˉ i = { Mean ( 1 ∣ V i T ∣ ∑ t = 0 T ∑ j ∈ V i w m , j , t ) Median ( 1 ∣ V i T ∣ ∑ t = 0 T ∑ j ∈ V i w m , j , t ) W ˉ = 1 I ∑ i ∈ I W ˉ i \bar{W}_i=\begin{cases} \text{Mean}(\frac{1}{|\mathcal{V_i}T|}\sum^T_{t=0}\sum_{j\in\mathcal{V}_i}w_{m,j,t})\\ \text{Median}(\frac{1}{|\mathcal{V_i}T|}\sum^T_{t=0}\sum_{j\in\mathcal{V}_i}w_{m,j,t}) \end{cases}\\ \bar{W}=\frac{1}{\mathcal{I}}\sum_{i\in\mathcal{I}}\bar{W}_i Wˉi={Mean(∣ViT∣1∑t=0T∑j∈Viwm,j,t)Median(∣ViT∣1∑t=0T∑j∈Viwm,j,t)Wˉ=I1i∈I∑Wˉi
结果
每个路口的策略都是通过不同的网络同时独立学习的,且 i i i路口的神经网络权值没有共享给其他路口的网络。
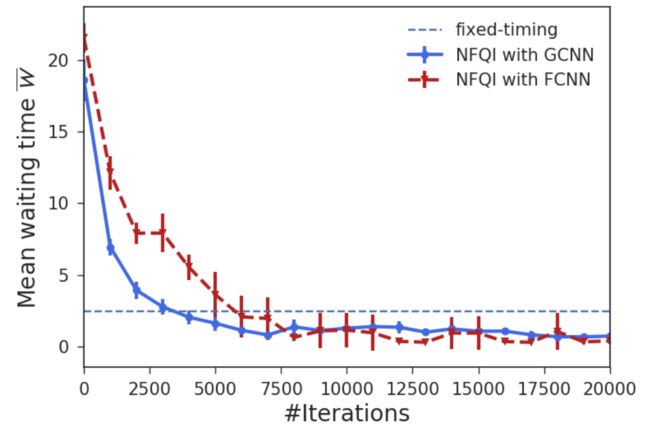
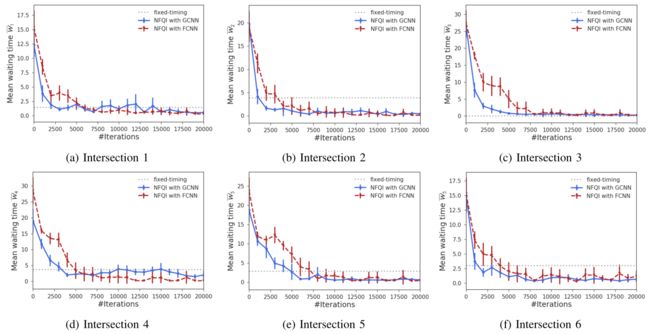
上图显示了在每个交叉口 i i i的平均等待时间 W ˉ i \bar{W}_i Wˉi和所有交叉口 W ˉ \bar{W} Wˉ的平均等待时间的学习曲线,图中的误差条表示95%的置信区间。结果表明,与固定时间控制相比,每个网络的NFQI收敛到更好的策略。
采用GCNN的NFQI较采用FCNN的NFQI收敛到可比策略的速度快两倍。这些结果是合理的,因为带有FCNN的NFQI包含了一个GCNN作为神经网络,但权重向量的大小比带有GCNN的NFQI大得多。
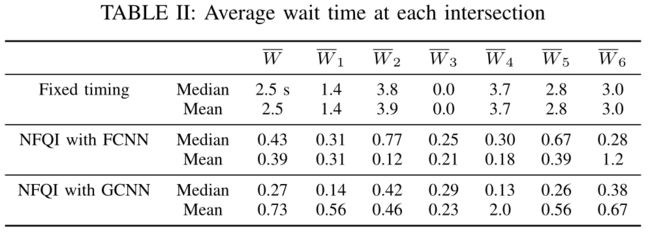
上表列出了第20000次迭代时每个交叉口的平均等待时间和中值。NFQI较固定定时控制等待时间短约2s。
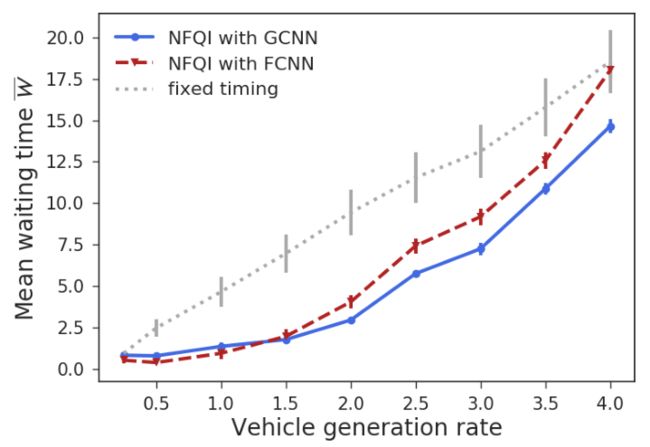
文章通过在训练过程中评估不同车辆生成率的比较方法来测试泛化性能。文章中模型算法学习了车辆生成率为0.5的策略,并测试了车辆生成率在0.25到4.0辆/秒之间的策略。上图显示了每个车辆生成率在所有路口的平均等待时间的平均值。图中的误差条表示95%的置信区间。由NFQI控制的交通信号在更大的车辆生成率范围内保持更短的等待时间。