【LeetCode】根据序列构造二叉树 (前序中序)(中序后序)

目录

105. 从前序与中序遍历序列构造二叉树

1.题目要求：

2.思路分析：

3.代码展示：

106. 从中序与后序遍历序列构造二叉树

1.题目要求：

2思路分析：

3.代码展示

---

105. 从前序与中序遍历序列构造二叉树

1.题目要求：

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

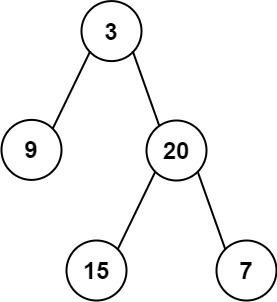
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均 无重复 元素
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

2.思路分析：

因为前序的遍历方式是根左右，所以我们可以用一个下标index遍历前序，寻找根节点，找到根节点后，我们需要在中序遍历中找到这个元素所在的下标，下标的左边都是左子树，右边都是右子树，最后运用递归解决

3.代码展示：

public TreeNode buildTree(int[] preorder, int[] inorder) {
        return buildTreeHelper(preorder,inorder,0,inorder.length - 1);
    }

    /**
     * 借助前序遍历，在中序遍历结果集[left...right]上还原二叉树
     * @param preorder
     * @param inorder
     * @param left
     * @param right
     * @return
     */
    // 当前处理到前序遍历的哪个结点了
    int index = 0;
    private TreeNode buildTreeHelper(int[] preorder, int[] inorder, int left, int right) {
        // base case
        if (index == preorder.length) {
            // 所有节点已经处理完毕
            return null;
        }
        if (left > right) {
            // 当前中序遍历的[left..right] 区间中没有元素
            return null;
        }
        // 1.先从前序遍历的结果集中找到根节点
        int val = preorder[index];
        index ++;
        TreeNode root = new TreeNode(val);
        // 2.再从中序遍历中找到当前树根的索引pos
        int pos = find(inorder,val);
        // 3.此时根据中序遍历的结果位置
        root.left = buildTreeHelper(preorder,inorder,left,pos - 1);
        root.right = buildTreeHelper(preorder,inorder,pos + 1,right);
        return root;
    }
    // 在当前中序遍历的结果集[left..right]找到待查找元素val的索引
    private int find(int[] inorder, int val) {
        for (int i = 0;i < inorder.length;i++) {
            if(inorder[i] == val) {
                return i;
            }
        }
        return -1;
    }

106. 从中序与后序遍历序列构造二叉树

1.题目要求：

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

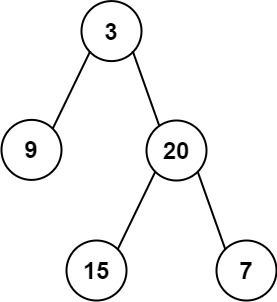
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder 和 postorder 都由 不同 的值组成
• postorder 中每一个值都在 inorder 中
• inorder 保证是树的中序遍历
• postorder 保证是树的后序遍历

2思路分析：

与前序遍历不同的是，后序遍历的方式是左右跟，所以我们只需将上述稍稍修改一下，

index从后往前遍历，递归先处理右子树，在处理左子树即可

3.代码展示

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private static int index;
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        index =  postorder.length- 1;
        return buildTreeHleper(inorder, postorder, 0, inorder.length - 1);
    }
    public TreeNode buildTreeHleper(int[] inorder, int[] postorder,int left, int right){
        if(index < 0){
            return null;
        }
        if(left > right){
            return null;
        }
        int c = postorder[index];
        index--;
        TreeNode root = new TreeNode(c);
        int pos = find(inorder, c);
        root.right = buildTreeHleper(inorder, postorder, pos + 1, right);
        root.left = buildTreeHleper(inorder, postorder, left, pos - 1);
        return root;
    }

    public int find(int[] inorder, int c){
        for(int i = 0 ; i < inorder.length; i++){
            if(inorder[i] == c){
                return i;
            }
        }
        return -1;
    }
}