浙大PTA数据结构与算法题目集(中文)题解集复习用
文章目录
-
- 7-1 最大子列和问题 (20分)(dp或贪心)
- 7-2 一元多项式的乘法与加法运算 (20分)
- 7-3 树的同构 (25分)
- 7-4 是否同一棵二叉搜索树 (25分)
- 7-5 堆中的路径 (25分)(数据结构--堆)
- 7-6 列出连通集 (25分)(BFS、DFS遍历图)
- 7-7 六度空间 (30分)(遍历节点进行BFS)
-
-
- 几个求最短路算法的比较与分析(面试前再看看)
-
- 7-8 哈利·波特的考试 (25分)(多源最短路floyd)
- 7-9 旅游规划 (25分)(单源最短路dijkstra)
-
-
- 求最小生成树算法的比较与分析
-
- 7-10 公路村村通 (30分)(最小生成树prim)
- 7-11 关键活动 (30分)
- 7-12 排序 (25分)
- 7-13 统计工龄 (20分)(桶排序或直接用map)
- 7-14 电话聊天狂人 (25分)(stl-map应用)
-
-
- std::[string](http://www.cplusplus.com/reference/string/string/)::compare
- Return Value
-
- 7-15 QQ帐户的申请与登陆 (25分)(用stl-map简单模拟)
- 7-16 一元多项式求导 (20分)
- 7-17 汉诺塔的非递归实现 (25分)
- 7-18 银行业务队列简单模拟 (25分)(模拟)
- 7-19 求链式线性表的倒数第K项 (20分)(vector简单使用)
- 7-23 还原二叉树 (25分)(树)
- 7-24 树种统计 (25分)(string类型的输入和输出)
- 7-25 朋友圈 (25分)(并查集)
- 7-26 Windows消息队列 (25分)(stl-priority_queue)
- 7-29 修理牧场 (25分)(优先队列实现哈夫曼树)
- 7-31 笛卡尔树 (25分)(BST判断的变式)
- 7-32 哥尼斯堡的“七桥问题” (25分)(欧拉回路)
- 7-33 地下迷宫探索 (30分)(dfs遍历图)
- 7-34 任务调度的合理性 (25分)(验证是否为拓扑序列)
- 7-36 社交网络图中结点的“重要性”计算 (30分)(无权图BFS)
- 7-37 模拟EXCEL排序 (25分)(重载sort函数进行自定义排序)
- 7-38 寻找大富翁 (25分)(优先队列实现最大堆)
- 7-39 魔法优惠券 (25分)(贪心)
- 7-40 奥运排行榜 (25分)
- 7-41 PAT排名汇总 (25分)
- 7-50 畅通工程之局部最小花费问题(最小生成树kruskal)
- 还是畅通工程
7-1 最大子列和问题 (20分)(dp或贪心)
给定K个整数组成的序列{ N1, N2, …, N**K },“连续子列”被定义为{ N**i, N**i+1, …, N**j },其中 1≤i≤j≤K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 },其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序,计算给定整数序列的最大子列和。
本题旨在测试各种不同的算法在各种数据情况下的表现。各组测试数据特点如下:
- 数据1:与样例等价,测试基本正确性;
- 数据2:102个随机整数;
- 数据3:103个随机整数;
- 数据4:104个随机整数;
- 数据5:105个随机整数;
输入格式:
输入第1行给出正整数K (≤100000);第2行给出K个整数,其间以空格分隔。
输出格式:
在一行中输出最大子列和。如果序列中所有整数皆为负数,则输出0。
输入样例:
6
-2 11 -4 13 -5 -2
输出样例:
20
#include
#include
using namespace std;
int main(){
//dp[i]表示到i为止最大的子数组和
//dp[i+1] = max(dp[i] + a[i], a[i])
int dp[100005]={0};
int a[100005];
int k;
cin>>k;
for(int i = 0; i < k; i++){
cin>>a[i];
}
int sum = -1;
dp[0] = a[0];
for(int i = 1; i < k; i++){
dp[i] = max(dp[i-1] + a[i], a[i]);
}
for(int i = 0; i < k; i++){
sum = max(sum, dp[i]);
}
if (sum < 0) sum = 0;
printf("%d", sum);
return 0;
}
7-2 一元多项式的乘法与加法运算 (20分)
设计函数分别求两个一元多项式的乘积与和。
输入格式:
输入分2行,每行分别先给出多项式非零项的个数,再以指数递降方式输入一个多项式非零项系数和指数(绝对值均为不超过1000的整数)。数字间以空格分隔。
输出格式:
输出分2行,分别以指数递降方式输出乘积多项式以及和多项式非零项的系数和指数。数字间以空格分隔,但结尾不能有多余空格。零多项式应输出0 0。
输入样例:
4 3 4 -5 2 6 1 -2 0
3 5 20 -7 4 3 1
输出样例:
15 24 -25 22 30 21 -10 20 -21 8 35 6 -33 5 14 4 -15 3 18 2 -6 1
5 20 -4 4 -5 2 9 1 -2 0
#include
using namespace std;
int main(){
int n, a[1005] ={0}, coff, exp, muti[2001] = {0}, add[1005]={0};
cin >> n;
for(int i = 0; i < n; i++){
cin >> coff >> exp;
a[exp] = coff;
add[exp] = coff;
}
cin >> n;
for(int i = 0; i < n; i++){
cin >> coff >> exp;
for(int j = 0; j < 1005; j++){
muti[exp + j] += a[j] * coff;
}
add[exp] += coff;
}
int cnt = 0;
for(int j = 2000; j >= 0; j--){
if(muti[j]!=0){
if(cnt){
cout<<" ";
}
cout << muti[j] <<" " <= 0; j--){
if(add[j]!=0){
if(cnt){
cout<<" ";
}
cout << add[j] <<" " < 7-3 树的同构 (25分)
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
![]()
图1
![]()
图2
现给定两棵树,请你判断它们是否是同构的。
输入格式:
输入给出2棵二叉树树的信息。对于每棵树,首先在一行中给出一个非负整数N (≤10),即该树的结点数(此时假设结点从0到N−1编号);随后N行,第i行对应编号第i个结点,给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意:题目保证每个结点中存储的字母是不同的。
输出格式:
如果两棵树是同构的,输出“Yes”,否则输出“No”。
输入样例1(对应图1):
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
输出样例1:
Yes
输入样例2(对应图2):
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
输出样例2:
No
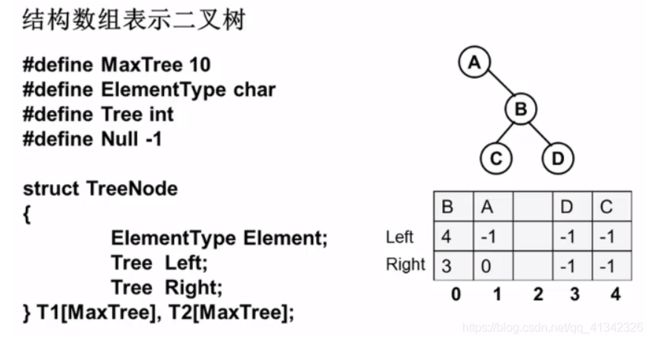
#include
#define MaxTree 10
#define ElementType char
#define Tree int
#define NULL -1
struct TreeNode
{
ElementType e;
Tree left;
Tree right;
} T1[MaxTree],T2[MaxTree];
Tree BuildTree ( struct TreeNode T[]);
int Isomorphic(Tree R1,Tree R2);
int main()
{
Tree R1,R2;
R1 = BuildTree(T1);
R2 = BuildTree(T2);
if( Isomorphic(R1,R2)){
printf("Yes\n");
}
else{
printf("No\n");
}
return 0;
}
Tree BuildTree ( struct TreeNode T[])
{
int i;
int n;
int check[MaxTree];
char cl,cr;
Tree root = NULL; //若n为0,返回NULL
scanf("%d",&n);
if( n )
{
for( i=0; i 7-4 是否同一棵二叉搜索树 (25分)
给定一个插入序列就可以唯一确定一棵二叉搜索树。然而,一棵给定的二叉搜索树却可以由多种不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树,都得到一样的结果。于是对于输入的各种插入序列,你需要判断它们是否能生成一样的二叉搜索树。
输入格式:
输入包含若干组测试数据。每组数据的第1行给出两个正整数N (≤10)和L,分别是每个序列插入元素的个数和需要检查的序列个数。第2行给出N个以空格分隔的正整数,作为初始插入序列。最后L行,每行给出N个插入的元素,属于L个需要检查的序列。
简单起见,我们保证每个插入序列都是1到N的一个排列。当读到N为0时,标志输入结束,这组数据不要处理。
输出格式:
对每一组需要检查的序列,如果其生成的二叉搜索树跟对应的初始序列生成的一样,输出“Yes”,否则输出“No”。
输入样例:
4 2
3 1 4 2
3 4 1 2
3 2 4 1
2 1
2 1
1 2
0
输出样例:
Yes
No
No
#include
using namespace std;
const int maxn = 1024 + 7;
int n, m;
int a[maxn], b[maxn];
void build1(){
memset(a, -1, sizeof a);
for(int i = 0; i < n; ++i){
int id = 1, x;
scanf("%d", &x);
while(1){
if(a[id] == -1){
a[id] = x;
break;
}
else if(x < a[id]){
id *= 2;
}
else id = 2*id+1;
}
}
}
void build2()
{
memset(b, -1, sizeof b);
for(int i = 0; i < n; ++i)
{
int id = 1, x;
scanf("%d", &x);
while(1)
{
if(b[id] == -1)
{
b[id] = x;
break;
}
else if(x < b[id])
{
id *= 2;
}
else id = 2*id+1;
}
}
}
int check()
{
for(int i = 1; i < maxn; ++i)
{
if(a[i] != b[i]) return 0;
}
return 1;
}
int main(){
while(cin>>n>>m){
if(n==0)
break;
build1();
for(int i = 0; i < m; ++i)
{
build2();
if(check()) cout<<"Yes"< //慕课上浙大老师的做法:7-4 是否同一棵二叉搜索树 (25分)
7-5 堆中的路径 (25分)(数据结构–堆)
将一系列给定数字插入一个初始为空的小顶堆H[]。随后对任意给定的下标i,打印从H[i]到根结点的路径。
输入格式:
每组测试第1行包含2个正整数N和M(≤1000),分别是插入元素的个数、以及需要打印的路径条数。下一行给出区间[-10000, 10000]内的N个要被插入一个初始为空的小顶堆的整数。最后一行给出M个下标。
输出格式:
对输入中给出的每个下标i,在一行中输出从H[i]到根结点的路径上的数据。数字间以1个空格分隔,行末不得有多余空格。
输入样例:
5 3
46 23 26 24 10
5 4 3
输出样例:
24 23 10
46 23 10
以前建堆都是处理完后离线操作,一系列sift,但是这样做与题目中建好的堆对应不了,只能边插入边调整,参考
7-5 堆中的路径 (25分)
#include
using namespace std;
#define maxn 1005
#define minn -10001
int heap[maxn], size;
void BuildHeap();
void insert(int);
int main(){
int n, m, t;
cin >> n >> m;
BuildHeap();
for(int i = 0; i < n; i++){
cin >> t;
insert(t);
}
for(int i = 0; i < m; i++){
cin >> t;
cout << heap[t];
while(t > 1){
cout << " " << heap[t/2];
t/=2;
}
cout < x; i/=2){
//小顶堆,如果父节点大于插入结点则二者交换
heap[i] = heap[i/2];
}
heap[i] = x;
}
7-6 列出连通集 (25分)(BFS、DFS遍历图)
给定一个有N个顶点和E条边的无向图,请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N−1编号。进行搜索时,假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。
输入格式:
输入第1行给出2个整数N(0<N≤10)和E,分别是图的顶点数和边数。随后E行,每行给出一条边的两个端点。每行中的数字之间用1空格分隔。
输出格式:
按照"{ v1 v2 … v**k }"的格式,每行输出一个连通集。先输出DFS的结果,再输出BFS的结果。
输入样例:
8 6
0 7
0 1
2 0
4 1
2 4
3 5
输出样例:
{ 0 1 4 2 7 }
{ 3 5 }
{ 6 }
{ 0 1 2 7 4 }
{ 3 5 }
{ 6 }
#include
#include
#include
using namespace std;
//输出有顺序,使用邻接矩阵存储方便遍历
int edge[15][15]={0};
bool vis[15];
int n, e;
void dfs(int index){
cout << index <<" ";
vis[index] = true;
for(int i = 0; i < n; i++){
if(!vis[i] && edge[index][i] == 1){
dfs(i);
}
}
return;
}
void bfs(int index){
queue q;
while(!q.empty()){
q.pop();
}
q.push(index);
vis[index] = true;
while(!q.empty()){
int top = q.front();
cout << top <<" ";
q.pop();
for(int i = 0; i < n; i++){
if(!vis[i] && edge[top][i] == 1){
q.push(i);
vis[i] = true;
}
}
}
return;
}
int main(){
cin >> n >> e;
//memeset在这里面
memset(vis, false, sizeof(vis));
for(int i = 0; i < e; i++){
int from, to;
cin >> from >> to;
edge[from][to] = edge[to][from] = 1;
}
for(int i = 0; i < n; i++){
if(!vis[i]){
cout <<"{ ";
dfs(i);
cout << "}" << endl;
}
}
for(int i = 0; i < n; i++){
vis[i] = false;
}
for(int i = 0; i < n; i++){
if(!vis[i]){
cout <<"{ ";
bfs(i);
cout << "}" << endl;
}
}
return 0;
}
7-7 六度空间 (30分)(遍历节点进行BFS)
“六度空间”理论又称作“六度分隔(Six Degrees of Separation)”理论。这个理论可以通俗地阐述为:“你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过五个人你就能够认识任何一个陌生人。”如图1所示。
![]()
图1 六度空间示意图
“六度空间”理论虽然得到广泛的认同,并且正在得到越来越多的应用。但是数十年来,试图验证这个理论始终是许多社会学家努力追求的目标。然而由于历史的原因,这样的研究具有太大的局限性和困难。随着当代人的联络主要依赖于电话、短信、微信以及因特网上即时通信等工具,能够体现社交网络关系的一手数据已经逐渐使得“六度空间”理论的验证成为可能。
假如给你一个社交网络图,请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。
输入格式:
输入第1行给出两个正整数,分别表示社交网络图的结点数N(1<N≤103,表示人数)、边数M(≤33×N,表示社交关系数)。随后的M行对应M条边,每行给出一对正整数,分别是该条边直接连通的两个结点的编号(节点从1到N编号)。
输出格式:
对每个结点输出与该结点距离不超过6的结点数占结点总数的百分比,精确到小数点后2位。每个结节点输出一行,格式为“结点编号:(空格)百分比%”。
输入样例:
10 9
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
输出样例:
1: 70.00%
2: 80.00%
3: 90.00%
4: 100.00%
5: 100.00%
6: 100.00%
7: 100.00%
8: 90.00%
9: 80.00%
10: 70.00%
#include
#include
#include
#include
using namespace std;
int n, m; //社交网络图的结点数N(1 q;
q.push(index);
cnt++;
vis[index] = 1;
while (q.size()) {
index = q.front();
for (int i = 1; i <= n; i++) {
if (a[index][i]&&!vis[i]) {
vis[i] = vis[index] + 1;
if (vis[i] < 8) {
q.push(i);
cnt++;
}
}
}
q.pop();
}
return cnt;
}
int main(){
cin >> n >> m;
for(int i = 0; i < m; i++){
int from, to;
cin >> from >> to;
a[from][to] = a[to][from] = 1;
}
for(int i = 1; i <= n; i++){
printf("%d: %.2f%%\n", i, 100.0*bfs(i)/n);
}
return 0;
}
几个求最短路算法的比较与分析(面试前再看看)
有权图的单源最短路算法:
方法1:直接扫描所有未收录顶点-O(|V|),时间复杂度T=O(|V2|+|E|),适合稠密图
方法2:将dist存在最小堆中-O(log|V|),更新dist[w]的值-O(log|V|),T=O(|V|log|V|+|E|log|V|) =O(|E|log|V|),对于稀疏图效果好
多源最短路算法:
方法1:直接将单源最短路算法调用|V|遍,T=O(|V|3+|E|×|V|),对于稀疏图效果好
方法2:Floyd算法,T=O(|V|3),适合稠密图
7-8 哈利·波特的考试 (25分)(多源最短路floyd)
哈利·波特要考试了,他需要你的帮助。这门课学的是用魔咒将一种动物变成另一种动物的本事。例如将猫变成老鼠的魔咒是haha,将老鼠变成鱼的魔咒是hehe等等。反方向变化的魔咒就是简单地将原来的魔咒倒过来念,例如ahah可以将老鼠变成猫。另外,如果想把猫变成鱼,可以通过念一个直接魔咒lalala,也可以将猫变老鼠、老鼠变鱼的魔咒连起来念:hahahehe。
现在哈利·波特的手里有一本教材,里面列出了所有的变形魔咒和能变的动物。老师允许他自己带一只动物去考场,要考察他把这只动物变成任意一只指定动物的本事。于是他来问你:带什么动物去可以让最难变的那种动物(即该动物变为哈利·波特自己带去的动物所需要的魔咒最长)需要的魔咒最短?例如:如果只有猫、鼠、鱼,则显然哈利·波特应该带鼠去,因为鼠变成另外两种动物都只需要念4个字符;而如果带猫去,则至少需要念6个字符才能把猫变成鱼;同理,带鱼去也不是最好的选择。
输入格式:
输入说明:输入第1行给出两个正整数N (≤100)和M,其中N是考试涉及的动物总数,M是用于直接变形的魔咒条数。为简单起见,我们将动物按1~N编号。随后M行,每行给出了3个正整数,分别是两种动物的编号、以及它们之间变形需要的魔咒的长度(≤100),数字之间用空格分隔。
输出格式:
输出哈利·波特应该带去考场的动物的编号、以及最长的变形魔咒的长度,中间以空格分隔。如果只带1只动物是不可能完成所有变形要求的,则输出0。如果有若干只动物都可以备选,则输出编号最小的那只。
输入样例:
6 11
3 4 70
1 2 1
5 4 50
2 6 50
5 6 60
1 3 70
4 6 60
3 6 80
5 1 100
2 4 60
5 2 80
输出样例:
4 70
7-8 哈利·波特的考试 (25分)
自己的代码没有人家写的清晰,贴一下这位大哥的代码,侵权立即删除。
#include
#include
#define MAXVEX 105
#define INFINITY 65535
void CreateGraph( );
void Floyd();
void FindAnimal();
int FindMax( int i);
int G[MAXVEX][MAXVEX],Nv,Ne;
int D[MAXVEX][MAXVEX]; //存储最短路径矩阵
int main()
{
CreateGraph();
FindAnimal();
return 0;
}
void CreateGraph()
{
//用邻接矩阵表示图
int i,j;
int v1,v2,w;
scanf("%d %d",&Nv,&Ne);
for( i=1; i<=Nv; i++)
{
for( j=1; j<=Nv; j++)
{
if( i==j){
G[i][j] = 0;
}
else G[i][j] = INFINITY; //初始化
}
}
for( i=0; imax )
{
min = max;
animal = i;
}
}
printf("%d %d\n",animal,min);
}
int FindMax( int i)
{
int max;
int j;
max = 0;
for( j=1; j<=Nv; j++)
{
if( i!=j && D[i][j]>max)
{
max = D[i][j];
}
}
return max;
}
void Floyd()
{
int i,j,k;
for( i=1; i<=Nv; i++)
{
for( j=1; j<=Nv; j++)
{
D[i][j] = G[i][j];
}
}
//注意动物是从下标1开始编号
for ( k=1; k<=Nv; k++)
{
for( i=1; i<=Nv; i++)
{
for( j=1; j<=Nv; j++)
{
if( D[i][k]+D[k][j] < D[i][j])
{
D[i][j] = D[i][k]+D[k][j];
}
}
}
}
}
7-9 旅游规划 (25分)(单源最短路dijkstra)
有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。
输入格式:
输入说明:输入数据的第1行给出4个正整数N、M、S、D,其中N(2≤N≤500)是城市的个数,顺便假设城市的编号为0~(N−1);M是高速公路的条数;S是出发地的城市编号;D是目的地的城市编号。随后的M行中,每行给出一条高速公路的信息,分别是:城市1、城市2、高速公路长度、收费额,中间用空格分开,数字均为整数且不超过500。输入保证解的存在。
输出格式:
在一行里输出路径的长度和收费总额,数字间以空格分隔,输出结尾不能有多余空格。
输入样例:
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20
输出样例:
3 40
以后变量起名一定短点,见名知义对于算法题不适用…
#include
#include
#include
#include
using namespace std;
#define N 505
int MAX = INT_MAX;
int graph[N][N], cost[N][N];
int dist[N], vis[N], mincost[N];
void dijkstra(int , int , int);
int main(){
int n, m, s, d;
cin >> n >> m >> s >> d;
//初始化
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
graph[i][j] = graph[j][i] = MAX;
cost[i][j] = cost[j][i] = MAX;
}
}
memset(vis, 0, sizeof(vis));
for(int i = 0; i < m; i++){
int from, to, len, c;
cin >> from >> to >> len >> c;
graph[from][to] = graph[to][from] = len;
cost[from][to] = cost[to][from] = c;
}
//以s作为起点,初始化dist数组
for(int i = 0; i < n; i++){
dist[i] = graph[s][i];
mincost[i] = cost[s][i];
}
dijkstra(s, n, d);
cout << dist[d] <<" " << mincost[d];
return 0;
}
void dijkstra(int s, int n, int d){
vis[s] = 1;
dist[s] = 0;
for(int i = 0; i < n -1; i++){
int minn = MAX, minindex = -1;
for(int j = 0; j < n; j++){
if(vis[j] == 0 && dist[j] < minn){
minn = dist[j];
minindex = j;
}
}
vis[minindex] = 1;
//选出最小的点要更新dist数组时,顺便把cost数组也更新了
//以刚选出的点minindex作为中转,遍历所有节点,查看能否做松弛操作
//即 看是否能有dist[j] > dist[minindex] + graph[minindex][j]
for(int j = 0; j < n; j++){
if(vis[j] == 0 && graph[minindex][j] < MAX && dist[minindex] + graph[minindex][j] < dist[j]){
dist[j] = dist[minindex] + graph[minindex][j];
mincost[j] = mincost[minindex] + cost[minindex][j];
}else if(vis[j]==0 && graph[minindex][j] < MAX && dist[minindex] + graph[minindex][j] == dist[j] && mincost[j]>mincost[minindex]+cost[minindex][j])
mincost[j] = mincost[minindex] + cost[minindex][j];
}
/*for(int i = 0; i < n; i++){
cout << "dist[i]:" << dist[i] <<" ";
}
cout < 求最小生成树算法的比较与分析
Prim算法:小树变大树,O(|V|2),适合稠密图
Kruskal算法:将森林合并成树,不用堆:O(|E|2);用堆优化以后:O(|E|log|E|),适合稀疏图
7-10 公路村村通 (30分)(最小生成树prim)
现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。
输入格式:
输入数据包括城镇数目正整数N(≤1000)和候选道路数目M(≤3N);随后的M行对应M条道路,每行给出3个正整数,分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见,城镇从1到N编号。
输出格式:
输出村村通需要的最低成本。如果输入数据不足以保证畅通,则输出−1,表示需要建设更多公路。
输入样例:
6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3
输出样例:
12
#include
#include
#include
using namespace std;
#define N 1005
const int INF = INT_MAX;
int g[N][N]; //邻接矩阵
bool visited[N]; //顶点是否已经进入S集合
int lowcost[N]; //从集合S到未被选中集合的最小权值
int n, m;
int Prim();
int main(){
cin >> n >> m;
//初始化
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
g[i][j] = g[j][i] = INF;
}
}
for(int i = 0; i < m; i++){
int from, to, cost;
cin >> from >> to >> cost;
g[from][to] = g[to][from] = cost;
}
cout << Prim() << endl;
return 0;
}
int Prim(){
for(int i = 1; i <= n; i++){
lowcost[i] = INF;
visited[i] = false;
}
//不要忘记初始化
for(int i = 2; i <= n; i++){
if(g[1][i]!=INF) lowcost[i] = g[1][i];
}
visited[1] = true;
lowcost[1] = 0;
/* for(int i = 1; i <= n; i++){
cout << lowcost[i] <<" ";
}*/
int res = 0;
for(int k = 1; k <= n-1; k++){//循环n-1次
int v = -1, minn = INF;
for(int i = 1; i <= n; i++){
if(!visited[i] && lowcost[i] < minn){
v = i;
minn = lowcost[i];
}
}
if(v == -1) return -1;
visited[v] = true;
res += lowcost[v];
// cout << "v:" << v <<" " << lowcost[v] << endl;
for(int i = 2; i <= n; i++){
lowcost[i] = min(lowcost[i], g[v][i]);
}
}
return res;
}
7-11 关键活动 (30分)
假定一个工程项目由一组子任务构成,子任务之间有的可以并行执行,有的必须在完成了其它一些子任务后才能执行。“任务调度”包括一组子任务、以及每个子任务可以执行所依赖的子任务集。
比如完成一个专业的所有课程学习和毕业设计可以看成一个本科生要完成的一项工程,各门课程可以看成是子任务。有些课程可以同时开设,比如英语和C程序设计,它们没有必须先修哪门的约束;有些课程则不可以同时开设,因为它们有先后的依赖关系,比如C程序设计和数据结构两门课,必须先学习前者。
但是需要注意的是,对一组子任务,并不是任意的任务调度都是一个可行的方案。比如方案中存在“子任务A依赖于子任务B,子任务B依赖于子任务C,子任务C又依赖于子任务A”,那么这三个任务哪个都不能先执行,这就是一个不可行的方案。
任务调度问题中,如果还给出了完成每个子任务需要的时间,则我们可以算出完成整个工程需要的最短时间。在这些子任务中,有些任务即使推迟几天完成,也不会影响全局的工期;但是有些任务必须准时完成,否则整个项目的工期就要因此延误,这种任务就叫“关键活动”。
请编写程序判定一个给定的工程项目的任务调度是否可行;如果该调度方案可行,则计算完成整个工程项目需要的最短时间,并输出所有的关键活动。
输入格式:
输入第1行给出两个正整数N(≤100)和M,其中N是任务交接点(即衔接相互依赖的两个子任务的节点,例如:若任务2要在任务1完成后才开始,则两任务之间必有一个交接点)的数量。交接点按1*N*编号,*M*是子任务的数量,依次编号为1M。随后M行,每行给出了3个正整数,分别是该任务开始和完成涉及的交接点编号以及该任务所需的时间,整数间用空格分隔。
输出格式:
如果任务调度不可行,则输出0;否则第1行输出完成整个工程项目需要的时间,第2行开始输出所有关键活动,每个关键活动占一行,按格式“V->W”输出,其中V和W为该任务开始和完成涉及的交接点编号。关键活动输出的顺序规则是:任务开始的交接点编号小者优先,起点编号相同时,与输入时任务的顺序相反。
输入样例:
7 8
1 2 4
1 3 3
2 4 5
3 4 3
4 5 1
4 6 6
5 7 5
6 7 2
输出样例:
17
1->2
2->4
4->6
6->7
时间宝贵,AOE写起来得有200行,贴上大哥的代码,跳过~
7-11 关键活动 (30分)
#include
#include
#define MAXVER 105
#define INFINITY 65535
int G[MAXVER][MAXVER]; //图
int early[MAXVER]; //最早发生时间
int late[MAXVER]; //最迟发生时间
int in[MAXVER]; //入度
int out[MAXVER]; //出度
int nv,ne; //顶点数目 ,边数目
void CreatGraph();
int EarlyTime();
void LateTime(int Scost);
int FindMax( int a,int b);
int FindMin( int a,int b);
int main()
{
int flag;
int i,j;
scanf("%d %d",&nv,&ne);
CreatGraph();
flag = EarlyTime();
if( flag==-1)
{
printf("0\n");
}
else
{
printf("%d\n",flag);
LateTime( flag );
for( i=1; i<=nv; i++)
{
if(early[i] != late[i])
continue;
for( j=nv; j>=1 ; j--)
{
if( G[i][j]>=0 && early[j]==late[j] &&late[j]-G[i][j]==early[i])
{
//i,j均在关键路径上且相邻
printf("%d->%d\n",i,j);
}
}
}
}
return 0;
}
void CreatGraph()
{
int i,j;
int s,d,cost;
for( i=1; i<=nv; i++)
{
for( j=1; j<=nv; j++)
{
G[i][j] = -1;
}
early[i] = 0;
late[i] = INFINITY;
in[i] = 0;
out[i] = 0;
}
for( i=0; i=0 )
{
in[i]--;
early[i] = FindMax( early[i],early[temp]+G[temp][i]);
if( in[i]==0)
{
queue[++rear] = i;
}
}
}
}
if( count!=nv)
{
ret = -1;
}
else
{
ret = early[1];
for( i=2; i<=nv; i++)
{
if(early[i] > ret)
{
//找出最大的early[i]
ret = early[i];
}
}
}
return ret;
}
void LateTime(int Scost)
{
int i;
int queue[MAXVER];
int first=-1,rear=-1;
int temp;
for( i=1; i<=nv; i++)
{
if( out[i]==0)
{
queue[++rear] = i;
late[i] = Scost;
}
}
while( first=1; i--)
{
if( G[i][temp]>=0)
{
late[i] = FindMin( late[i],late[temp]-G[i][temp]);
out[i]--;
if(out[i]==0)
{
queue[++rear] = i;
}
}
}
}
}
int FindMax( int a,int b)
{
if( a>b )
{
return a;
}
else
{
return b;
}
}
int FindMin( int a,int b)
{
if( a>b )
{
return b;
}
else
{
return a;
}
}
7-12 排序 (25分)
给定N个(长整型范围内的)整数,要求输出从小到大排序后的结果。
本题旨在测试各种不同的排序算法在各种数据情况下的表现。各组测试数据特点如下:
- 数据1:只有1个元素;
- 数据2:11个不相同的整数,测试基本正确性;
- 数据3:103个随机整数;
- 数据4:104个随机整数;
- 数据5:105个随机整数;
- 数据6:105个顺序整数;
- 数据7:105个逆序整数;
- 数据8:105个基本有序的整数;
- 数据9:105个随机正整数,每个数字不超过1000。
输入格式:
输入第一行给出正整数N(≤105),随后一行给出N个(长整型范围内的)整数,其间以空格分隔。
输出格式:
在一行中输出从小到大排序后的结果,数字间以1个空格分隔,行末不得有多余空格。
输入样例:
11
4 981 10 -17 0 -20 29 50 8 43 -5
输出样例:
-20 -17 -5 0 4 8 10 29 43 50 981
#include
#include
using namespace std;
void print(int *a, int n);
void insert_sort(int *a, int n);
void bin_insertsort(int *a, int n);
void shell_sort(int *a, int n);
void bubble_sort(int *a, int n);
void quick_sort(int *a, int left, int right);
int Partition(int *a, int left, int right);
/*堆排序*/
void sift(int *a, int low, int high);
void heap_sort(int *a, int n);
int main(){
int n, a[100005];
scanf("%d", &n);
for(int i = 0; i < n; i++){
scanf("%d", &a[i]);
}
//三种插入排序
//insert_sort(a, n);
//bin_insertsort(a, n);
//shell_sort(a, n);
//两种交换排序
//bubble_sort(a, n);
//quick_sort(a, 0, n-1);
//两种选择排序,简单选择排序select_sort不写了
heap_sort(a, n);
//还有归并排序和基数排序,适合用作外排
//...
print(a, n);
return 0;
}
void heap_sort(int *a, int n){
for(int i=(n-1)/2; i>=0; i--){
sift(a, i, n-1);
}
for(int i=n-1; i>=1;){
swap(a[i], a[0]);
i--;
sift(a, 0, i);
}
}
void sift(int *a, int low, int high){
int i = low, j = 2*i+1;
int temp = a[i];
while(j <= high){
if(j < high && a[j]= temp) {
right--;
}
a[left] = a[right];
while (left < right && a[left] <= temp) {
left++;
}
a[right] = a[left];
}
a[left] = temp; // 基准归位
return left; // 返回基准位置
}
void bubble_sort(int *a, int n){
int flag = 0;
for(int i = 0; i < n-1; i++){//进行n-1趟排序
for(int j = n-1; j > i; j--){
if (a[j] < a[j - 1]) {
int temp = a[j];
a[j] = a[j - 1];
a[j - 1] = temp;
flag = 1;
}
}
if(!flag) break;
}
}
void shell_sort(int *a, int n){
for(int d=n/2; d>=1; d/=2){
for(int i = d; i < n; i++){ // 0, 0 + dk, 0 + 2*dk...
int temp = a[i];
if(a[i-d] > temp){
int j = i-d;
for(; j>=0 && a[j]>temp; j-=d){
a[j+d] = a[j];
}
a[j+d] = temp;
}
}
}
}
void bin_insertsort(int *a, int n){
for(int i = 1; i < n; i++){
int left = 0, right = i-1, temp = a[i], mid;
while(left <= right){
mid = (right + left)/2;
if(temp < a[mid]){
right = mid-1;
}else{
left = mid+1;
}
}
//此处a[left] > temp,将a[left~i-1]后移一位
for(int j = i-1; j>=left; j--){
a[j+1] = a[j];
}
a[left] = temp;
}
}
//插入排序
void insert_sort(int *a, int n){
//初始0~0作为有序区,之后有序区为0~i,逐渐扩大
for(int i = 1; i < n; i++){
if(a[i] < a[i-1]){
int temp = a[i];
int j = i - 1;
for(; j>=0 && temp < a[j]; j--){
a[j+1] = a[j];
}
a[j+1] = temp;
}
}
}
void print(int *a, int n){
int flag = 0;
for(int i = 0; i < n; i++){
if(flag){
printf(" ");
}else{
flag = 1;
}
printf("%d", a[i]);
}
//printf("\n");
}
排序算法比较
| 名称 | 最坏时间复杂度 | 平均时间复杂度 | 最好时间复杂度 | 空间复杂度 | 是否稳定 | 比较次数 | 排序总趟数 |
|---|---|---|---|---|---|---|---|
| 直接插入排序 | O(n2),初始完全逆序 | O(n2) | O(n),初始完全顺序 | O(1) | 稳定 | 最好n-1次,最坏n(n-1)/2次 | n-1趟 |
| 折半插入排序 | O(n2) | O(n2) | O(n) | O(1) | 稳定 | 最好n-1次,最坏应该是(log1+log2+…log(n-1)*n-1次。要注意的是虽然比较次数少了,但是元素的移动次数并没有减少,初始序列有多少逆序对,就有多少次移动次数。 | n-1趟 |
| 希尔排序 | O(n2) | O(1) | 不稳定 | 与增量序列、子序列的排序算法有关 | 与增量序列有关 | ||
| 冒泡排序 | O(n2) | O(n2) | O(n) | O(1) | 稳定 | 最好n-1次,最坏n(n-1)/2次 | n-1趟 |
| 快速排序 | O(n2) | O(nlog2n) | O(nlog2n) | O(log2n),最坏情况下会达到O(n) | 不稳定 | 与初始序列顺序有关 | 最好logn趟,最坏n-1趟 |
| 简单选择排序 | O(n2) | O(n2) | O(n2) | O(1) | 不稳定 | n(n-1)/2次 | n-1趟,每趟找一个最小值 |
| 堆排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(1) | 不稳定 | 定理:堆排序处理N个不同元素的随机排列的平均比较次数是2NlogN-O(NloglogN) | |
| 归并排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | O(n) | 稳定 | ||
| 基数排序 | O(d(n+r)) | O(d(n+r)) | O(d(n+r)) | O® | 稳定 |
7-13 统计工龄 (20分)(桶排序或直接用map)
给定公司N名员工的工龄,要求按工龄增序输出每个工龄段有多少员工。
输入格式:
输入首先给出正整数N(≤105),即员工总人数;随后给出N个整数,即每个员工的工龄,范围在[0, 50]。
输出格式:
按工龄的递增顺序输出每个工龄的员工个数,格式为:“工龄:人数”。每项占一行。如果人数为0则不输出该项。
输入样例:
8
10 2 0 5 7 2 5 2
输出样例:
0:1
2:3
5:2
7:1
10:1
#include
#include 7-14 电话聊天狂人 (25分)(stl-map应用)
给定大量手机用户通话记录,找出其中通话次数最多的聊天狂人。
输入格式:
输入首先给出正整数N(≤105),为通话记录条数。随后N行,每行给出一条通话记录。简单起见,这里只列出拨出方和接收方的11位数字构成的手机号码,其中以空格分隔。
输出格式:
在一行中给出聊天狂人的手机号码及其通话次数,其间以空格分隔。如果这样的人不唯一,则输出狂人中最小的号码及其通话次数,并且附加给出并列狂人的人数。
输入样例:
4
13005711862 13588625832
13505711862 13088625832
13588625832 18087925832
15005713862 13588625832
输出样例:
13588625832 3
#include
#include std::string::compare
Return Value
Returns a signed integral indicating the relation between the strings:
| value | relation between compared string and comparing string |
|---|---|
0 |
They compare equal |
<0 |
Either the value of the first character that does not match is lower in the compared string, or all compared characters match but the compared string is shorter. |
>0 |
Either the value of the first character that does not match is greater in the compared string, or all compared characters match but the compared string is longer. |
7-15 QQ帐户的申请与登陆 (25分)(用stl-map简单模拟)
实现QQ新帐户申请和老帐户登陆的简化版功能。最大挑战是:据说现在的QQ号码已经有10位数了。
输入格式:
输入首先给出一个正整数N(≤105),随后给出N行指令。每行指令的格式为:“命令符(空格)QQ号码(空格)密码”。其中命令符为“N”(代表New)时表示要新申请一个QQ号,后面是新帐户的号码和密码;命令符为“L”(代表Login)时表示是老帐户登陆,后面是登陆信息。QQ号码为一个不超过10位、但大于1000(据说QQ老总的号码是1001)的整数。密码为不小于6位、不超过16位、且不包含空格的字符串。
输出格式:
针对每条指令,给出相应的信息:
1)若新申请帐户成功,则输出“New: OK”;
2)若新申请的号码已经存在,则输出“ERROR: Exist”;
3)若老帐户登陆成功,则输出“Login: OK”;
4)若老帐户QQ号码不存在,则输出“ERROR: Not Exist”;
5)若老帐户密码错误,则输出“ERROR: Wrong PW”。
输入样例:
5
L 1234567890 [email protected]
N 1234567890 [email protected]
N 1234567890 [email protected]
L 1234567890 myQQ@qq
L 1234567890 [email protected]
输出样例:
ERROR: Not Exist
New: OK
ERROR: Exist
ERROR: Wrong PW
Login: OK
#include
#include 7-16 一元多项式求导 (20分)
设计函数求一元多项式的导数。
输入格式:
以指数递降方式输入多项式非零项系数和指数(绝对值均为不超过1000的整数)。数字间以空格分隔。
输出格式:
以与输入相同的格式输出导数多项式非零项的系数和指数。数字间以空格分隔,但结尾不能有多余空格。
输入样例:
3 4 -5 2 6 1 -2 0
输出样例:
12 3 -10 1 6 0
#include
#include
int main(){
int coff, exp;
int flag = 0;
while(scanf("%d %d",&coff,&exp)!=EOF){
if(exp){
if( flag )
printf(" "); //如果不是第一个数就先输出一个空格
else
flag = 1;
printf("%d %d",coff*exp,exp-1);
}
else break;
}
if(!flag){
printf("0 0");
}
return 0;
}
7-17 汉诺塔的非递归实现 (25分)
借助堆栈以非递归(循环)方式求解汉诺塔的问题(n, a, b, c),即将N个盘子从起始柱(标记为“a”)通过借助柱(标记为“b”)移动到目标柱(标记为“c”),并保证每个移动符合汉诺塔问题的要求。
输入格式:
输入为一个正整数N,即起始柱上的盘数。
输出格式:
每个操作(移动)占一行,按柱1 -> 柱2的格式输出。
输入样例:
3
输出样例:
a -> c
a -> b
c -> b
a -> c
b -> a
b -> c
a -> c
递归实现,cout会超时,用printf比较快:
#include
#include
using namespace std;
int main(){
void hanoi(int n, char one, char two, char three);
int n;
cin >> n;
hanoi(n, 'a', 'b', 'c');
return 0;
}
//将n个盘子从one座借助two座,移动到three座
void hanoi(int n, char one, char two, char three){
if(n == 1){
printf("%c -> %c\n",one, three);
}else{
//先递归的解决n-1规模的问题, 将A塔中n-1个盘子借助C塔移动到B塔
hanoi(n-1, one, three, two);
//然后将最大的盘子移动到C塔
printf("%c -> %c\n",one, three);
hanoi(n-1, two, one, three);
}
}
非递归实现
7-18 银行业务队列简单模拟 (25分)(模拟)
设某银行有A、B两个业务窗口,且处理业务的速度不一样,其中A窗口处理速度是B窗口的2倍 —— 即当A窗口每处理完2个顾客时,B窗口处理完1个顾客。给定到达银行的顾客序列,请按业务完成的顺序输出顾客序列。假定不考虑顾客先后到达的时间间隔,并且当不同窗口同时处理完2个顾客时,A窗口顾客优先输出。
输入格式:
输入为一行正整数,其中第1个数字N(≤1000)为顾客总数,后面跟着N位顾客的编号。编号为奇数的顾客需要到A窗口办理业务,为偶数的顾客则去B窗口。数字间以空格分隔。
输出格式:
按业务处理完成的顺序输出顾客的编号。数字间以空格分隔,但最后一个编号后不能有多余的空格。
输入样例:
8 2 1 3 9 4 11 13 15
输出样例:
1 3 2 9 11 4 13 15
7-19 求链式线性表的倒数第K项 (20分)(vector简单使用)
给定一系列正整数,请设计一个尽可能高效的算法,查找倒数第K个位置上的数字。
输入格式:
输入首先给出一个正整数K,随后是若干非负整数,最后以一个负整数表示结尾(该负数不算在序列内,不要处理)。
输出格式:
输出倒数第K个位置上的数据。如果这个位置不存在,输出错误信息NULL。
输入样例:
4 1 2 3 4 5 6 7 8 9 0 -1
输出样例:
7
#include
#include
using namespace std;
int main(){
vector a;
int n, x;
scanf("%d", &n);
while(1){
scanf("%d", &x);
if(x < 0) break;
a.push_back(x);
}
int count = a.size();
if(n>0 && n<=count) cout< 7-23 还原二叉树 (25分)(树)
给定一棵二叉树的先序遍历序列和中序遍历序列,要求计算该二叉树的高度。
输入格式:
输入首先给出正整数N(≤50),为树中结点总数。下面两行先后给出先序和中序遍历序列,均是长度为N的不包含重复英文字母(区别大小写)的字符串。
输出格式:
输出为一个整数,即该二叉树的高度。
输入样例:
9
ABDFGHIEC
FDHGIBEAC
输出样例:
5
可以建树后再找树的高度,也可以递归的遍历序列,递归树的最大深度就是树的高度。
#include
#include
#include
using namespace std;
int depth(char *a, char *b, int len){
if(len==0) return 0;
int i;
//先序序列中遍历顺序:根左右,对应中序序列的节点左边是左子树,右边是右子树
for(i = 0; i < len; i++){
if(b[i] == a[0]){
break;
}
}
//在b[0]~b[i-1]搜索左子树,
int x = depth(a+1, b, i) + 1;
//在b[i+1]~b[n-i]搜索右子树
int y = depth(a+i+1, b+i+1, len-i-1) + 1;
return x > y ? x : y;
}
int main(){
char a[52]; //first_order
char b[52]; //in_order
int n;
cin >> n;
cin >> a >> b;
cout << depth(a, b, n);
return 0;
}
7-24 树种统计 (25分)(string类型的输入和输出)
随着卫星成像技术的应用,自然资源研究机构可以识别每一棵树的种类。请编写程序帮助研究人员统计每种树的数量,计算每种树占总数的百分比。
输入格式:
输入首先给出正整数N(≤105),随后N行,每行给出卫星观测到的一棵树的种类名称。种类名称由不超过30个英文字母和空格组成(大小写不区分)。
输出格式:
按字典序递增输出各种树的种类名称及其所占总数的百分比,其间以空格分隔,保留小数点后4位。
输入样例:
29
Red Alder
Ash
Aspen
Basswood
Ash
Beech
Yellow Birch
Ash
Cherry
Cottonwood
Ash
Cypress
Red Elm
Gum
Hackberry
White Oak
Hickory
Pecan
Hard Maple
White Oak
Soft Maple
Red Oak
Red Oak
White Oak
Poplan
Sassafras
Sycamore
Black Walnut
Willow
输出样例:
Ash 13.7931%
Aspen 3.4483%
Basswood 3.4483%
Beech 3.4483%
Black Walnut 3.4483%
Cherry 3.4483%
Cottonwood 3.4483%
Cypress 3.4483%
Gum 3.4483%
Hackberry 3.4483%
Hard Maple 3.4483%
Hickory 3.4483%
Pecan 3.4483%
Poplan 3.4483%
Red Alder 3.4483%
Red Elm 3.4483%
Red Oak 6.8966%
Sassafras 3.4483%
Soft Maple 3.4483%
Sycamore 3.4483%
White Oak 10.3448%
Willow 3.4483%
Yellow Birch 3.4483%
难点是输入和输出
#include
#include
#include
7-25 朋友圈 (25分)(并查集)
某学校有N个学生,形成M个俱乐部。每个俱乐部里的学生有着一定相似的兴趣爱好,形成一个朋友圈。一个学生可以同时属于若干个不同的俱乐部。根据“我的朋友的朋友也是我的朋友”这个推论可以得出,如果A和B是朋友,且B和C是朋友,则A和C也是朋友。请编写程序计算最大朋友圈中有多少人。
输入格式:
输入的第一行包含两个正整数N(≤30000)和M(≤1000),分别代表学校的学生总数和俱乐部的个数。后面的M行每行按以下格式给出1个俱乐部的信息,其中学生从1~N编号:
第i个俱乐部的人数Mi(空格)学生1(空格)学生2 … 学生Mi
输出格式:
输出给出一个整数,表示在最大朋友圈中有多少人。
输入样例:
7 4
3 1 2 3
2 1 4
3 5 6 7
1 6
输出样例:
4
并查集及其优化详解
#include
#include
using namespace std;
const int MAXN = 30005;
int f[MAXN], res[MAXN];
int Find(int x){
if(f[x]!=x)
f[x] = Find(f[x]);
return f[x];
}
void Union(int x, int y){
int p1 = Find(x);
int p2 = Find(y);
f[p1] = p2;
}
int main(){
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++){
f[i] = i;
}
for(int i = 0; i < m; i++){
int x, root;
scanf("%d%d", &x, &root);
root = Find(root);
for(int k = 0; k < x-1; k++){
int t;
scanf("%d", &t);
Union(root, t);
}
}
int ans = 0;
for(int i = 1; i <= n; i++){
int root = Find(i);
res[root]++;
ans = max(ans, res[root]);
}
cout << ans;
return 0;
}
7-26 Windows消息队列 (25分)(stl-priority_queue)
消息队列是Windows系统的基础。对于每个进程,系统维护一个消息队列。如果在进程中有特定事件发生,如点击鼠标、文字改变等,系统将把这个消息加到队列当中。同时,如果队列不是空的,这一进程循环地从队列中按照优先级获取消息。请注意优先级值低意味着优先级高。请编辑程序模拟消息队列,将消息加到队列中以及从队列中获取消息。
输入格式:
输入首先给出正整数N(≤105),随后N行,每行给出一个指令——GET或PUT,分别表示从队列中取出消息或将消息添加到队列中。如果指令是PUT,后面就有一个消息名称、以及一个正整数表示消息的优先级,此数越小表示优先级越高。消息名称是长度不超过10个字符且不含空格的字符串;题目保证队列中消息的优先级无重复,且输入至少有一个GET。
输出格式:
对于每个GET指令,在一行中输出消息队列中优先级最高的消息的名称和参数。如果消息队列中没有消息,输出EMPTY QUEUE!。对于PUT指令则没有输出。
输入样例:
9
PUT msg1 5
PUT msg2 4
GET
PUT msg3 2
PUT msg4 4
GET
GET
GET
GET
输出样例:
msg2
msg3
msg4
msg1
EMPTY QUEUE!
#include
#include
#include
using namespace std;
struct news{
char name[12];
int pqlevel;
friend bool operator <(news a, news b){
return a.pqlevel > b.pqlevel;
}
};
int main(){
int n;
char op[10];
priority_queue pq;
cin >> n;
for(int i = 1; i <= n; i++){
scanf("%s", op);
if(op[0] == 'P'){
struct news t;
scanf("%s%d", t.name, &t.pqlevel);
pq.push(t);
}else if(op[0] == 'G'){
if(pq.empty()){
printf("EMPTY QUEUE!\n");
}
else{
struct news t = pq.top();
printf("%s\n", t.name);
pq.pop() ;
}
}
}
return 0;
}
priority_queue常用操作
-
(constructor)
Construct priority queue (public member function )
-
empty
Test whether container is empty (public member function )
-
size
Return size (public member function )
-
top
Access top element (public member function )
-
push
Insert element (public member function )
-
emplace
Construct and insert element (public member function )
-
pop
Remove top element (public member function )
-
swap
Swap contents (public member function )
7-29 修理牧场 (25分)(优先队列实现哈夫曼树)
农夫要修理牧场的一段栅栏,他测量了栅栏,发现需要N块木头,每块木头长度为整数L**i个长度单位,于是他购买了一条很长的、能锯成N块的木头,即该木头的长度是L**i的总和。
但是农夫自己没有锯子,请人锯木的酬金跟这段木头的长度成正比。为简单起见,不妨就设酬金等于所锯木头的长度。例如,要将长度为20的木头锯成长度为8、7和5的三段,第一次锯木头花费20,将木头锯成12和8;第二次锯木头花费12,将长度为12的木头锯成7和5,总花费为32。如果第一次将木头锯成15和5,则第二次锯木头花费15,总花费为35(大于32)。
请编写程序帮助农夫计算将木头锯成N块的最少花费。
输入格式:
输入首先给出正整数N(≤104),表示要将木头锯成N块。第二行给出N个正整数(≤50),表示每段木块的长度。
输出格式:
输出一个整数,即将木头锯成N块的最少花费。
输入样例:
8
4 5 1 2 1 3 1 1
输出样例:
49
C++ priority_queue底层是用堆实现的
#include
#include
#include
using namespace std;
int main(){
int n;
priority_queue, greater> pq;
cin >> n;
for(int i = 0; i < n; i++){
int x;
scanf("%d", &x);
pq.push(x);
}
int ans = 0;
while(pq.size()>1){
int a = pq.top();
pq.pop();
int b = pq.top();
pq.pop();
int t = a + b;
cout << t< 7-31 笛卡尔树 (25分)(BST判断的变式)
笛卡尔树是一种特殊的二叉树,其结点包含两个关键字K1和K2。首先笛卡尔树是关于K1的二叉搜索树,即结点左子树的所有K1值都比该结点的K1值小,右子树则大。其次所有结点的K2关键字满足优先队列(不妨设为最小堆)的顺序要求,即该结点的K2值比其子树中所有结点的K2值小。给定一棵二叉树,请判断该树是否笛卡尔树。
输入格式:
输入首先给出正整数N(≤1000),为树中结点的个数。随后N行,每行给出一个结点的信息,包括:结点的K1值、K2值、左孩子结点编号、右孩子结点编号。设结点从0~(N-1)顺序编号。若某结点不存在孩子结点,则该位置给出−1。
输出格式:
输出YES如果该树是一棵笛卡尔树;否则输出NO。
输入样例1:
6
8 27 5 1
9 40 -1 -1
10 20 0 3
12 21 -1 4
15 22 -1 -1
5 35 -1 -1
输出样例1:
YES
输入样例2:
6
8 27 5 1
9 40 -1 -1
10 20 0 3
12 11 -1 4
15 22 -1 -1
50 35 -1 -1
输出样例2:
NO
可以递归的判断BST,函数一定要传一个区间,否则就会出现子树都满足要求,但整个树不满足的情况。
比如:
3
/ \
2 4
/ \
1 3
每一个子树都满足性质,但整个树不满足性质,所以判断BST一定要传入一段区间
另外判断是否是BST还可以建树,利用BST的中序遍历是从小到大的有序序列这个性质
#include
#include
#include
#include
using namespace std;
const int INF = INT_MAX;
const int MIN = INT_MIN;
struct Node{
int k1, k2, lchild, rchild;
}node[1005];
bool IsVaild(int i, int k1_min, int k1_max){
int lchild = node[i].lchild, rchild = node[i].rchild;
int k1 = node[i].k1, k2 = node[i].k2;
if(lchild == -1 && rchild == -1) //空树返回真
return true;
if(lchild!=-1){ //左树不为空
if(node[lchild].k1 >= k1 || node[lchild].k1 <= k1_min) //左树不满足BST性质
return false;
if(node[lchild].k2 <= k2) //是否满足最小堆的性质
return false;
}
if(rchild!=-1){ //右树不为空
if(node[rchild].k1 <= k1 || node[rchild].k1 >= k1_max) //右树不满足BST性质
return false;
if(node[rchild].k2 <= k2) //是否满足最小堆的性质
return false;
}
bool flag1 = true, flag2 = true;
if(lchild != -1){
flag1 = IsVaild(lchild, k1_min, k1);
}
if(rchild != -1){
flag2 = IsVaild(rchild, k1, k1_max);
}
return flag1 && flag2;
}
int main(){
int n;
cin >> n;
int root = -1;
int vis[1005]={0};
for(int i = 0; i < n; i++){
cin >> node[i].k1 >> node[i].k2 >> node[i].lchild >> node[i].rchild;
}
//找根节点
for(int i = 0; i < n; i++){
vis[node[i].lchild] = 1;
vis[node[i].rchild] = 1;
}
for(int i = 0; i < n; i++){
if(!vis[i]) {
root = i;
break;
}
}
if(IsVaild(root, MIN, INF)){
cout << "YES";
}else{
cout << "NO";
}
return 0;
}
7-32 哥尼斯堡的“七桥问题” (25分)(欧拉回路)
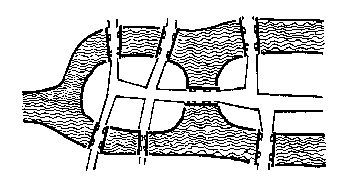
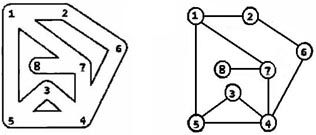
哥尼斯堡是位于普累格河上的一座城市,它包含两个岛屿及连接它们的七座桥,如下图所示。
可否走过这样的七座桥,而且每桥只走过一次?瑞士数学家欧拉(Leonhard Euler,1707—1783)最终解决了这个问题,并由此创立了拓扑学。
这个问题如今可以描述为判断欧拉回路是否存在的问题。欧拉回路是指不令笔离开纸面,可画过图中每条边仅一次,且可以回到起点的一条回路。现给定一个无向图,问是否存在欧拉回路?
输入格式:
输入第一行给出两个正整数,分别是节点数N (1≤N≤1000)和边数M;随后的M行对应M条边,每行给出一对正整数,分别是该条边直接连通的两个节点的编号(节点从1到N编号)。
输出格式:
若欧拉回路存在则输出1,否则输出0。
输入样例1:
6 10
1 2
2 3
3 1
4 5
5 6
6 4
1 4
1 6
3 4
3 6
输出样例1:
1
输入样例2:
5 8
1 2
1 3
2 3
2 4
2 5
5 3
5 4
3 4
输出样例2:
0
1.欧拉通路、欧拉回路、欧拉图
无向图:
- 设G是连通无向图,则称经过G的每条边一次并且仅一次的路径为欧拉通路;
- 如果欧拉通路是回路(起点和终点是同一个顶点),则称此回路为欧拉回路(Euler circuit);
- 具有欧拉回路的无向图G称为欧拉图(Euler graph)。
有向图:- 设D是有向图,D的基图连通,则称经过D的每条边一次并且仅一次的有向路径为有向欧拉通路;
- 如果有向欧拉通路是有向回路,则称此有向回路为有向欧拉回路(directed Euler circuit);
- 具有有向欧拉回路的有向图D称为有向欧拉图(directed Euler graph)。
2.欧拉回路的应用
- 哥尼斯堡七桥问题
- 一笔画问题。
- 旋转鼓轮的设计
3.欧拉回路的判定
判断欧拉路是否存在的方法
有向图:图连通,有一个顶点出度大入度1,有一个顶点入度大出度1,其余都是出度=入度。
无向图:图连通,只有两个顶点是奇数度,其余都是偶数度的。
判断欧拉回路是否存在的方法
有向图:图连通,所有的顶点出度=入度。
无向图:图连通,所有顶点都是偶数度。
https://blog.csdn.net/flx413/article/details/53471609
#include
using namespace std;
#define MAXN 1010
int a[MAXN][MAXN]={0},vis[MAXN]= {0},cnt[MAXN]= {0};
int n, m, b, c;
void dfs(int cur){
vis[cur] = 1;
for(int i = 1; i <= n; i++){
if(!vis[i] && a[cur][i]){
dfs(i);
}
}
return;
}
int main(){
cin >> n >> m;
for(int i = 0; i < m; i++){
scanf("%d%d", &b, &c); //别用cin
a[b][c]=a[c][b] = 1;
cnt[b]++; //记录每一个顶点的度数
cnt[c]++;
}
dfs(1);
int f = 1;
for(int i=1; i<=n; i++){
if(!vis[i] || cnt[i]%2 == 1){//是否存在奇数度数的顶点
f = 0;
break;
}
}
cout << f;
return 0;
}
7-33 地下迷宫探索 (30分)(dfs遍历图)
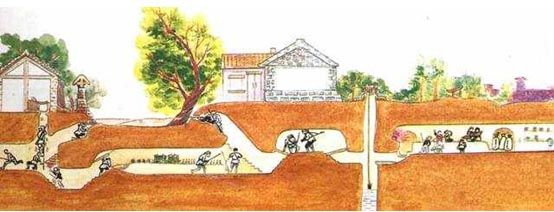
地道战是在抗日战争时期,在华北平原上抗日军民利用地道打击日本侵略者的作战方式。地道网是房连房、街连街、村连村的地下工事,如下图所示。
我们在回顾前辈们艰苦卓绝的战争生活的同时,真心钦佩他们的聪明才智。在现在和平发展的年代,对多数人来说,探索地下通道或许只是一种娱乐或者益智的游戏。本实验案例以探索地下通道迷宫作为内容。
假设有一个地下通道迷宫,它的通道都是直的,而通道所有交叉点(包括通道的端点)上都有一盏灯和一个开关。请问你如何从某个起点开始在迷宫中点亮所有的灯并回到起点?
输入格式:
输入第一行给出三个正整数,分别表示地下迷宫的节点数N(1<N≤1000,表示通道所有交叉点和端点)、边数M(≤3000,表示通道数)和探索起始节点编号S(节点从1到N编号)。随后的M行对应M条边(通道),每行给出一对正整数,分别是该条边直接连通的两个节点的编号。
输出格式:
若可以点亮所有节点的灯,则输出从S开始并以S结束的包含所有节点的序列,序列中相邻的节点一定有边(通道);否则虽然不能点亮所有节点的灯,但还是输出点亮部分灯的节点序列,最后输出0,此时表示迷宫不是连通图。
由于深度优先遍历的节点序列是不唯一的,为了使得输出具有唯一的结果,我们约定以节点小编号优先的次序访问(点灯)。在点亮所有可以点亮的灯后,以原路返回的方式回到起点。
输入样例1:
6 8 1
1 2
2 3
3 4
4 5
5 6
6 4
3 6
1 5
输出样例1:
1 2 3 4 5 6 5 4 3 2 1
输入样例2:
6 6 6
1 2
1 3
2 3
5 4
6 5
6 4
输出样例2:
6 4 5 4 6 0
#include
using namespace std;
#define MAXN 1010
int a[MAXN][MAXN]= {0}, vis[MAXN]= {0};
int cnt = 1, n, m, s, f=0;
void dfs(int x){
if(f)
printf(" ");
f++;
printf("%d", x);
for(int i = 1; i <= n; i++){
if(!vis[i]&&a[x][i]){
vis[i] = 1;
cnt++;
dfs(i);
printf(" %d", x);
}
}
}
int main()
{
cin >> n >> m >> s;
for(int i = 1; i <= m; i++){
int b,c;
scanf("%d%d", &b, &c);
a[b][c] = a[c][b] = 1;
}
vis[s] = 1;
dfs(s);
if(cnt < n)
cout<<" 0";
return 0;
}
7-34 任务调度的合理性 (25分)(验证是否为拓扑序列)
假定一个工程项目由一组子任务构成,子任务之间有的可以并行执行,有的必须在完成了其它一些子任务后才能执行。“任务调度”包括一组子任务、以及每个子任务可以执行所依赖的子任务集。
比如完成一个专业的所有课程学习和毕业设计可以看成一个本科生要完成的一项工程,各门课程可以看成是子任务。有些课程可以同时开设,比如英语和C程序设计,它们没有必须先修哪门的约束;有些课程则不可以同时开设,因为它们有先后的依赖关系,比如C程序设计和数据结构两门课,必须先学习前者。
但是需要注意的是,对一组子任务,并不是任意的任务调度都是一个可行的方案。比如方案中存在“子任务A依赖于子任务B,子任务B依赖于子任务C,子任务C又依赖于子任务A”,那么这三个任务哪个都不能先执行,这就是一个不可行的方案。你现在的工作是写程序判定任何一个给定的任务调度是否可行。
输入格式:
输入说明:输入第一行给出子任务数N(≤100),子任务按1~N编号。随后N行,每行给出一个子任务的依赖集合:首先给出依赖集合中的子任务数K,随后给出K个子任务编号,整数之间都用空格分隔。
输出格式:
如果方案可行,则输出1,否则输出0。
输入样例1:
12
0
0
2 1 2
0
1 4
1 5
2 3 6
1 3
2 7 8
1 7
1 10
1 7
输出样例1:
1
输入样例2:
5
1 4
2 1 4
2 2 5
1 3
0
输出样例2:
0
#include
using namespace std;
#define MAXN 105
int a[MAXN] = {0}, g[MAXN][MAXN];//a[i]为节点i的入度
int main(){
int m, n, t;
cin >> n;
for(int i = 1; i <= n; i++){
cin >> m;
for(int j = 1; j <= m; j++){
cin >> t;
g[t][i] = 1;
a[i]++;
}
}
queue q;
for(int i = 1; i <= n; i++){
if(a[i]==0) q.push(i);
}
while(q.size() > 0){
int cur = q.front();
q.pop();
for(int i = 1; i <= n; i++){
if(g[cur][i]!=0){
a[i]--;
if(a[i] == 0){
q.push(i);
}
}
}
}
int f = 1;
for(int i = 1; i <= n; i++){
if(a[i]!=0){ //经过拓扑排序后还有入度为0的点,说明有向图有回路了
f = 0;
break;
}
}
cout << f;
}
7-36 社交网络图中结点的“重要性”计算 (30分)(无权图BFS)
在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来。他们受到这些关系的影响,这种影响可以理解为网络中相互连接的结点之间蔓延的一种相互作用,可以增强也可以减弱。而结点根据其所处的位置不同,其在网络中体现的重要性也不尽相同。
“紧密度中心性”是用来衡量一个结点到达其它结点的“快慢”的指标,即一个有较高中心性的结点比有较低中心性的结点能够更快地(平均意义下)到达网络中的其它结点,因而在该网络的传播过程中有更重要的价值。在有N个结点的网络中,结点v**i的“紧密度中心性”C**c(v**i)数学上定义为v**i到其余所有结点v**j (j≠i) 的最短距离d(v**i,v**j)的平均值的倒数:
[外链图片转存中…(img-4w9tVr9J-1598540353529)]
对于非连通图,所有结点的紧密度中心性都是0。
给定一个无权的无向图以及其中的一组结点,计算这组结点中每个结点的紧密度中心性。
输入格式:
输入第一行给出两个正整数N和M,其中N(≤104)是图中结点个数,顺便假设结点从1到N编号;M(≤105)是边的条数。随后的M行中,每行给出一条边的信息,即该边连接的两个结点编号,中间用空格分隔。最后一行给出需要计算紧密度中心性的这组结点的个数K(≤100)以及K个结点编号,用空格分隔。
输出格式:
按照Cc(i)=x.xx的格式输出K个给定结点的紧密度中心性,每个输出占一行,结果保留到小数点后2位。
输入样例:
9 14
1 2
1 3
1 4
2 3
3 4
4 5
4 6
5 6
5 7
5 8
6 7
6 8
7 8
7 9
3 3 4 9
输出样例:
Cc(3)=0.47
Cc(4)=0.62
Cc(9)=0.35
定点和边都不小,但是需要计算”重要性“的不多,没必要计算全部节点,这是一个无权图,每次询问的时候,做一次BFS就好了。
#include
#include
#include
#include
using namespace std;
#define maxn 10005
double bfs(int x, int n);
vector adj[maxn]; //用vector存边
int vis[maxn];
int main(){
int n, m, k;
cin >> n >> m;
for(int i = 0; i < m; i++){
int a, b;
scanf("%d%d", &a, &b);
adj[a].push_back(b);
adj[b].push_back(a); //别忘了是个无向图
}
cin >> k;
for(int i = 0; i < k; i++){
int target;
scanf("%d", &target);
printf("Cc(%d)=%.2f\n", target, bfs(target, n));
}
return 0;
}
double bfs(int x, int n){
for(int i = 1; i <= n; i++){
vis[i] = -1;
}
vis[x] = 0; //vis[i]表示点x到i的最小距离
double sum = 0;
int cnt = 1;
queue q;
q.push(x);
while(!q.empty()){
int cur = q.front();
int len = adj[cur].size();
for(int i = 0; i < len; i++){
int next = adj[cur][i];
if(vis[next] == -1){
vis[next] = vis[cur] + 1;
sum += vis[next];
cnt++;
q.push(next);
}
}
q.pop();
}
if(cnt < n)
return 0;
// cout <<"sum:"<< sum << endl;
double res = (n-1)/sum;
return res;
}
7-37 模拟EXCEL排序 (25分)(重载sort函数进行自定义排序)
Excel可以对一组纪录按任意指定列排序。现请编写程序实现类似功能。
输入格式:
输入的第一行包含两个正整数N(≤105) 和C,其中N是纪录的条数,C是指定排序的列号。之后有 N行,每行包含一条学生纪录。每条学生纪录由学号(6位数字,保证没有重复的学号)、姓名(不超过8位且不包含空格的字符串)、成绩([0, 100]内的整数)组成,相邻属性用1个空格隔开。
输出格式:
在N行中输出按要求排序后的结果,即:当C=1时,按学号递增排序;当C=2时,按姓名的非递减字典序排序;当C=3时,按成绩的非递减排序。当若干学生具有相同姓名或者相同成绩时,则按他们的学号递增排序。
输入样例:
3 1
000007 James 85
000010 Amy 90
000001 Zoe 60
输出样例:
000001 Zoe 60
000007 James 85
000010 Amy 90
#include
using namespace std;
struct student{
char sno[7];
char name[10];
int score;
}s[100005];
bool cmp1(student a, student b){
if(strcmp(a.sno, b.sno)>0){
return b.sno < a.sno;
}
return b.sno > a.sno;
}
bool cmp2(student a, student b){
if(strcmp(a.name, b.name)>0){
return b.name < a.name;
}
return b.name > a.name;
}
bool cmp3(student a, student b){
if(a.score == b.score){
if(strcmp(a.sno, b.sno)>0){
return b.sno < a.sno;
}
return b.sno > a.sno;
}
return a.score < b.score;
}
int main(){
int n, c;
cin >> n >> c;
for(int i = 0; i < n; i++){
scanf("%s%s%d", s[i].sno, s[i].name, &s[i].score);
}
if(c == 1){
sort(s, s+n, cmp1);
for(int i = 0; i < n; i++){
printf("%s %s %d\n", s[i].sno, s[i].name, s[i].score);
}
}else if(c == 2){
sort(s, s+n, cmp2);
for(int i = 0; i < n; i++){
printf("%s %s %d\n", s[i].sno, s[i].name, s[i].score);
}
}else if(c == 3){
sort(s, s+n, cmp3);
for(int i = 0; i < n; i++){
printf("%s %s %d\n", s[i].sno, s[i].name, s[i].score);
}
}
return 0;
}
7-38 寻找大富翁 (25分)(优先队列实现最大堆)
胡润研究院的调查显示,截至2017年底,中国个人资产超过1亿元的高净值人群达15万人。假设给出N个人的个人资产值,请快速找出资产排前M位的大富翁。
输入格式:
输入首先给出两个正整数N(≤106)和M(≤10),其中N为总人数,M为需要找出的大富翁数;接下来一行给出N个人的个人资产值,以百万元为单位,为不超过长整型范围的整数。数字间以空格分隔。
输出格式:
在一行内按非递增顺序输出资产排前M位的大富翁的个人资产值。数字间以空格分隔,但结尾不得有多余空格。
输入样例:
8 3
8 12 7 3 20 9 5 18
输出样例:
20 18 12
#include
#include
#include
using namespace std;
int main(){
int n, k;
priority_queue, less> pq;//less规定优先队列的顺序为从大到小排列,即队头为最大的
cin >> n >> k;
for(int i = 0; i < n; i++){
int x;
scanf("%d", &x);
pq.push(x);
}
int flag = 0;
while(k-- && pq.size()>0){
if(flag){
cout << " ";
}else{
flag = 1;
}
int t = pq.top();
pq.pop();
cout < 7-39 魔法优惠券 (25分)(贪心)
在火星上有个魔法商店,提供魔法优惠券。每个优惠劵上印有一个整数面值K,表示若你在购买某商品时使用这张优惠劵,可以得到K倍该商品价值的回报!该商店还免费赠送一些有价值的商品,但是如果你在领取免费赠品的时候使用面值为正的优惠劵,则必须倒贴给商店K倍该商品价值的金额…… 但是不要紧,还有面值为负的优惠劵可以用!(真是神奇的火星)
例如,给定一组优惠劵,面值分别为1、2、4、-1;对应一组商品,价值为火星币M$7、6、-2、-3,其中负的价值表示该商品是免费赠品。我们可以将优惠劵3用在商品1上,得到M$28的回报;优惠劵2用在商品2上,得到M$12的回报;优惠劵4用在商品4上,得到M$3的回报。但是如果一不小心把优惠劵3用在商品4上,你必须倒贴给商店M$12。同样,当你一不小心把优惠劵4用在商品1上,你必须倒贴给商店M$7。
规定每张优惠券和每件商品都只能最多被使用一次,求你可以得到的最大回报。
输入格式:
输入有两行。第一行首先给出优惠劵的个数N,随后给出N个优惠劵的整数面值。第二行首先给出商品的个数M,随后给出M个商品的整数价值。N和M在[1, 106]之间,所有的数据大小不超过230,数字间以空格分隔。
输出格式:
输出可以得到的最大回报。
输入样例:
4 1 2 4 -1
4 7 6 -2 -3
输出样例:
43
给定两组数字,求这两组数字乘积的最大和
排序后贪心,每次取乘积为正的并且最大的乘积
#include
#include
#include
using namespace std;
#define maxn 1000005
int main(){
int a[maxn], b[maxn];
int n;
cin >> n;
for(int i = 0; i < n; i++){
scanf("%d", &a[i]);
}
cin >> n;
for(int i = 0; i < n; i++){
scanf("%d", &b[i]);
}
sort(a, a+n);
sort(b, b+n);
int sum = 0;
int i;
for(i = n-1; i>=0; i--){ //正*正 = 正
if(a[i]>0 && b[i]>0){
sum += a[i]*b[i];
}else{
break;
}
}
for(int j = 0; j < i; j++){ //负*负 = 负
if(a[j]<0 && b[j]<0){
sum += a[j]*b[j];
}else{
break;
}
}
cout << sum;
return 0;
}
7-40 奥运排行榜 (25分)
7-41 PAT排名汇总 (25分)
都是排序题,先跳过
7-50 畅通工程之局部最小花费问题(最小生成树kruskal)
某地区经过对城镇交通状况的调查,得到现有城镇间快速道路的统计数据,并提出“畅通工程”的目标:使整个地区任何两个城镇间都可以实现快速交通(但不一定有直接的快速道路相连,只要互相间接通过快速路可达即可)。现得到城镇道路统计表,表中列出了任意两城镇间修建快速路的费用,以及该道路是否已经修通的状态。现请你编写程序,计算出全地区畅通需要的最低成本。
输入格式:
输入的第一行给出村庄数目N (1≤N≤100);随后的N(N−1)/2行对应村庄间道路的成本及修建状态:每行给出4个正整数,分别是两个村庄的编号(从1编号到N),此两村庄间道路的成本,以及修建状态 — 1表示已建,0表示未建。
输出格式:
输出全省畅通需要的最低成本。
输入样例:
4
1 2 1 1
1 3 4 0
1 4 1 1
2 3 3 0
2 4 2 1
3 4 5 0
输出样例:
3
https://www.cnblogs.com/littlepage/p/13125668.html
```C++
#include 还是畅通工程
题目描述
某省调查乡村交通状况,得到的统计表中列出了任意两村庄间的距离。省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通(但不一定有直接的公路相连,只要能间接通过公路可达即可),并要求铺设的公路总长度为最小。请计算最小的公路总长度。
输入描述:
测试输入包含若干测试用例。每个测试用例的第1行给出村庄数目N ( < 100 );随后的N(N-1)/2行对应村庄间的距离,每行给出一对正整数,分别是两个村庄的编号,以及此两村庄间的距离。为简单起见,村庄从1到N编号。
当N为0时,输入结束,该用例不被处理。
输出描述:
对每个测试用例,在1行里输出最小的公路总长度。
示例1
输入
3
1 2 1
1 3 2
2 3 4
4
1 2 1
1 3 4
1 4 1
2 3 3
2 4 2
3 4 5
0
输出
3
5
#include