【python】math函数库介绍及其例题
math库的引用
1.import math
对math库中函数采用math.()形式使用
2.from math import<函数名>
对math库中函数可以直接采用<函数名>()形式使用
math库
math库包括四个数学常数
![]()
math库的数值表示函数
![]()
math库的三角运算函数
math库的高等特殊函数
![]()
例1:
在 3 行中分别输入一个浮点数,利用下面公式计算并输出 x 的值,严格保留小数点后2位数字。
import math
a = float(input())
b = float(input())
c = float(input())
v = math.pow(b,2)-4*a*c
if v < 0:
print("结束计算,没有结果。")
else:
z = math.sqrt(v)
x = (-b + z)/(2 * a)
print('%.2f'%x)运行结果:
例:
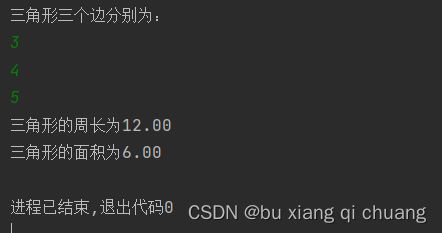
分三行输入 3 个浮点数,表示三角形的三个边长a、b、c 的长度,计算并依次输出三角形的周长和面积,结果严格保留2位小数。测试用例的数据保证三角形三边数据可以构成三角形。
三角形面积计算公式:
![]()
,其中s=(a+b+c)/2。
import math
print("三角形三个边分别为:")
a = float(input())
b = float(input())
c = float(input())
if a+b>c and a+c>b and b+c>a:
l = a + b + c
area = math.sqrt(l/2 * (l/2 - a) * (l/2 - b) * (l/2-c))
print(f'三角形的周长为{l:.2f}')
print(f'三角形的面积为{area:.2f}')
else:
print("不能构成三角形。")
运行结果:
例:
如下图,AB 是圆的一条弦,ABC形成一个弓形,在两行中分别输入AB和CD的长度,计算并分两行依次输出该圆的半径和弓形ABC的面积,结果均严格保留小数点后2位有效数字,应用三角函数和反三角函数时查阅math模块文档或利用自动补全完成。
提示:
从图中可知:
AD = AB / 2 OA2 = AD2 + OD2 OD = OC – CD = OA – CD
代入后可得
OA = (AD2 + CD2 ) / (2 * CD) sin(∠AOB / 2) = AD / OA
圆心角:
∠AOB = 2 * arcsin(AD / OA)
扇形AOB的面积为:
area_of_sector = ∠AOB / (2π) * π *OA2
三角形 △AOB
area_of_triangle = 1 / 2 * OA2 * sin(∠AOB)
弓形面积为扇形AOB面积减去三角形△AOB面积之差:
area_of_arch = area_of_sector - area_of_triangle
输入
分2行输入2个浮点数
输出
在两行内分别输出半径和弓形面积
import math
a = float(input('AB的值为:'))
b = float(input('CD的值为:'))
r = b/2 + math.pow(a,2)/8*b #圆半径
x = 2 * math.asin(a/2/r) #角AOB
area_of_sector = x/(2*math.pi) * math.pi * math.pow(r,2) #扇形AOB面积
area_of_triangle = 1/2 * math.pow(r,2) * a/r * (r - b)/r #三角形AOB面积
area_of_arch = area_of_sector - area_of_triangle #弓形ABC面积
print(f'圆半径为:{r:.2f}')
print(f'弓形ABC面积为:{area_of_arch:.2f}')运行结果: