深度学习算法及卷积神经网络
目录标题
-
-
- 传统神经网络
-
- 矩阵计算：
- 正则化：
- 激活函数sigmoid
- 损失函数
- 前向传播
- 激活函数Relu
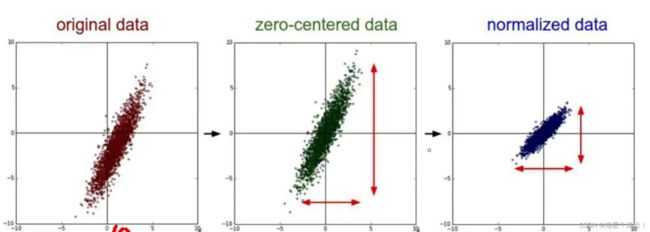
- 数据预处理
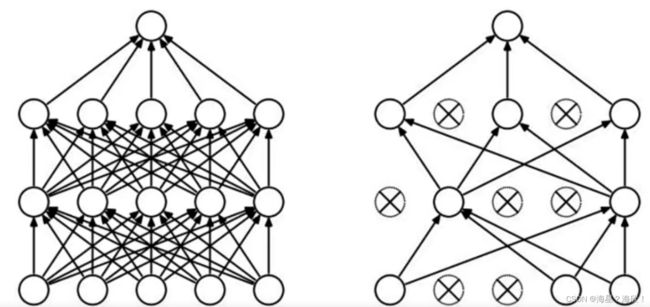
- DROP-OUT
- 卷积神经网络(CNN)
-
- 1.CNN网络的构成
- 2. 卷积层
-
- 2.1 卷积的计算⽅法
- 2.2 padding
- 2.3 stride
- 2.4 多通道卷积
- 2.5 多卷积核卷积
- 2..6 特征图大小
- 3. 池化层(Pooling)
-
- 3.1 最⼤池化
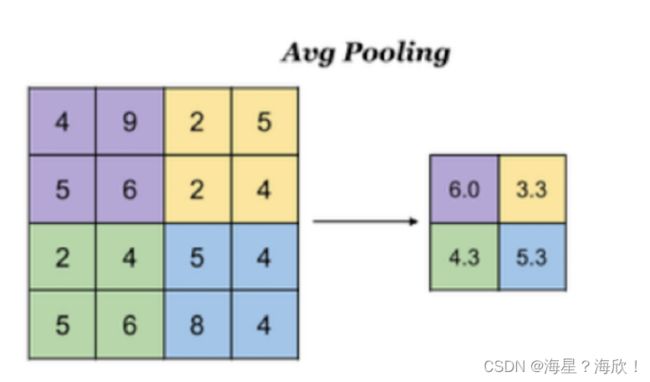
- 3.2 平均池化
- 4. 全连接层
-
传统神经网络
深度学习不适用情况：跨域（股票预测问题），旧历史数据的规律不适合新数据的规律
矩阵计算：
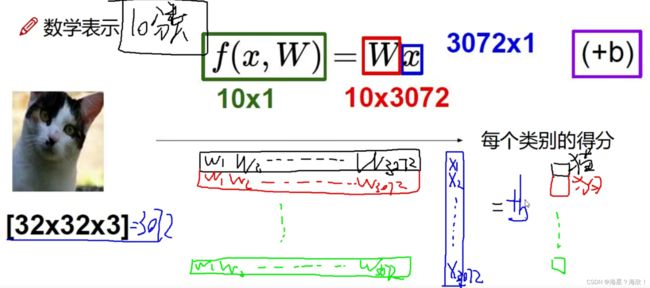
输入数据x[32×32×3]=3072个像素点，展开成一列，
目的：做一个10分类，10组权重参数，得到10个值，属于各个类别的概率
偏置项b,10个值
权重参数W得到：先随机，or预训练模型，
创新：修改损失函数。
损失函数：说明预测与实际的差异，差异越大说明W越不好需要大调，差异越小W微调
正则化：
W1和W2 与x的结果相同，但不代表w1和w2是一样的，w1只关注局部特征（偏科，随x变化剧烈，容易受异常点影响），w2关注全局（均衡，变化稳定）
如何体现出w1和w2的区别？-----正则化惩罚（防止过拟合）
异常点处理：最好在进入模型人工处理掉（比赛数据里面）
L2惩罚项：
损失函数 = 数据损失 + 正则化惩罚项
正则化L2惩罚项：
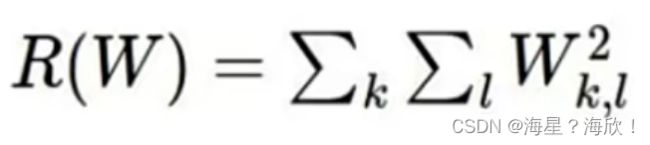
激活函数sigmoid
分类问题，希望得到的是一个概率值。但模型出来的数据什么都可能，如何做？—映射
sigmoid函数：
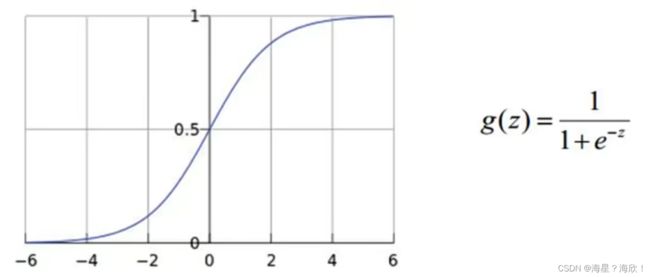
梯度消失问题：数值越大，梯度越接近0，更新不了行为参数，神经网络是一个传一个的模型，这个问题导致了97年到12年一直没有发展
神经网络：多个线性回归与逻辑回归的组和
损失函数
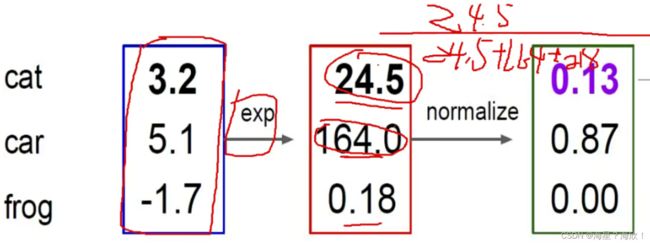
得到预测值后，
1，先把差异放大（加个指数函数ex ）
2，再用归一化转化为概率值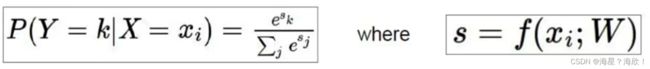
3，计算损失值：只考虑正确类别的概率值，越接近1损失值越接近0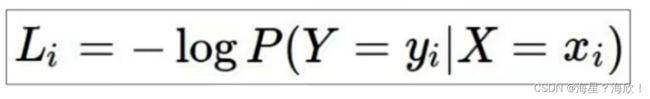
log函数：
前向传播
反向传播（即梯度下降）
神经网络：把人类理解的特征转化成，计算机理解的特征
隐藏层1：特征1 = 0.7H-0.1W+0.6A，。。。
中间数–权重
特征变换：Wx+b变成一组新特征
隐藏层2再做一遍，找到更适合的特征。
W和b的大小个数：
激活函数Relu
如果只引入线性，解决的问题有限–引入非线性函数
Relu:小于0的特征直接删掉了，
越重要的特征越学越大
数据预处理
去均值：
标准化
DROP-OUT
不用全部的神经元，防止过拟合
随机杀死神经元：
卷积神经网络(CNN)
利⽤全连接神经⽹络对图像进⾏处理存在以下两个问题：
- 需要处理的数据量⼤，效率低
- 图像在维度调整的过程中很难保留原有的特征，导致图像处理的准确率不⾼
1.CNN网络的构成
CNN⽹络受⼈类视觉神经系统的启发
CNN⽹络主要有三部分构成：
- 卷积层、池化层和全连接层构成，其中卷积层负责提取图像中的局部特征；
- 池化层⽤来⼤幅降低参数量级(降维)；
- 全连接层类似⼈⼯神经⽹络的部分，⽤来输出想要的结果。
2. 卷积层
2.1 卷积的计算⽅法
卷积层的⽬的是提取输⼊特征图的特征
如何卷积：原始图像，要提取这个图像上的特征，与卷积核进行一个卷积（把卷积核在图像上进行一个遍历），输出一个特征结果
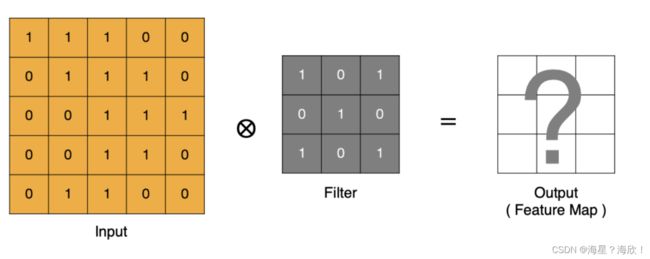
卷积运算本质上就是在滤波器和输⼊数据的局部区域间做点积。
点计算⽅法，同理可以计算其他各点，得到最终的卷积结果。
最后结果作为特征图输出
2.2 padding
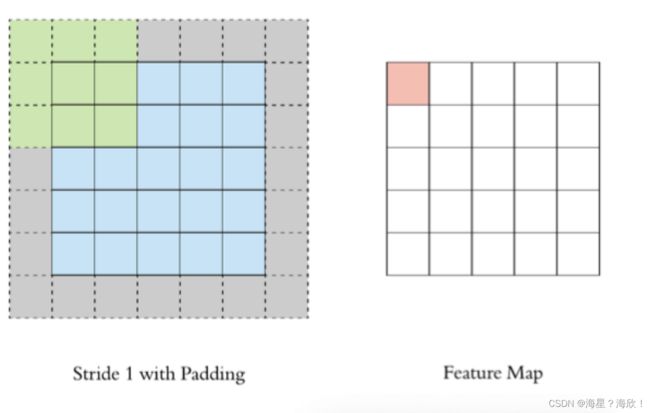
要保证结果与原图大小一样，通过padding
在上述卷积过程中，特征图⽐原始图减⼩了很多，我们可以在原图像的周围进⾏padding,来保证在卷积过程中特征图⼤⼩不变。
进行0来填充：
55的图，要输出55的特征图：
2.3 stride
步长的设计：步长为1，也可以把stride增⼤,⽐如设为2，也是可以提取特征图的，如下图所示：
2.4 多通道卷积
前面是单通道的，下面看多通道的
计算⽅法如下：当输⼊有多个通道（channel）时(例如图⽚可以有 RGB三个通道)，卷积核需要拥有相同的channel数,每个卷积核 channel 与输⼊层的对应 channel 进⾏卷积，将每个 channel 的卷积结果按位相加得到最终的 Feature Map
2.5 多卷积核卷积
当有多个卷积核时，每个卷积核学习到不同的特征，对应产⽣包含多个 channel 的 Feature Map,
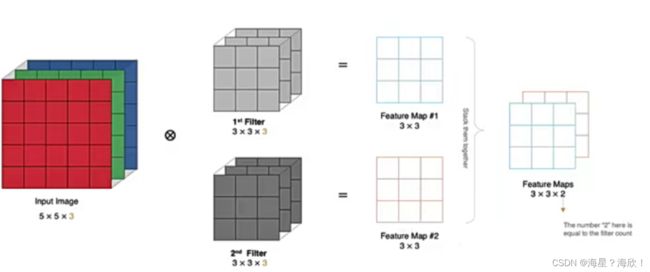
n个卷积核产生n个 Feature Map
2…6 特征图大小
输出特征图的⼤⼩与以下参数息息相关：
- size:卷积核/过滤器⼤⼩，⼀般会选择为奇数，⽐如有1* 1， 3 *3， 5 *5
- padding：零填充的⽅式
- stride:步⻓
在tf.keras中实现：
tf.keras.layers.MaxPool2D(pool_size=(2, 2), strides=None, padding='valid')
#pool_size: 池化窗⼝的⼤⼩
#strides: 窗⼝移动的步⻓，默认为1
#padding: 是否进⾏填充，默认是不进⾏填充的
3. 池化层(Pooling)
池化层迎来降低了后续⽹络层的输⼊维度，缩减模型⼤⼩，提⾼计算速度，并提⾼了Feature Map 的鲁棒性，防⽌过拟合，
它主要对卷积层学习到的特征图进⾏下采样（subsampling）处理，主要由两种：
3.1 最⼤池化
Max Pooling,取窗⼝内的最⼤值作为输出，这种⽅式使⽤较⼴泛
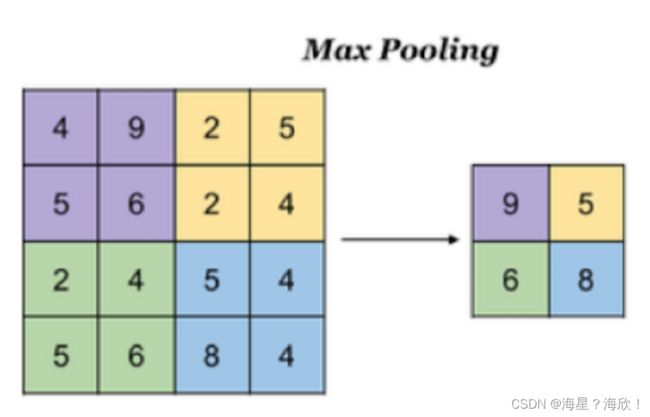
3.2 平均池化
Avg Pooling,取窗⼝内的所有值的均值作为输出
4. 全连接层
全连接层位于CNN⽹络的末端，经过卷积层的特征提取与池化层的降维后，将特征图转换成⼀维向量送⼊到全连接层中进⾏分类或回归的操作。
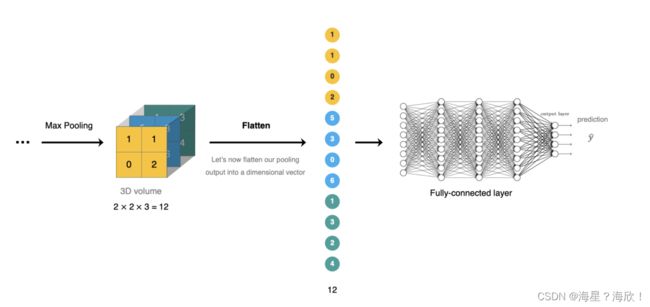
flatten展开，特征图展开