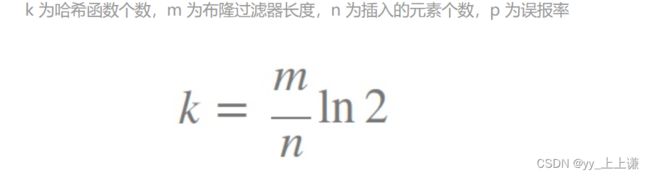【C++、数据结构】位图、布隆过滤器、哈希切割（哈希思想的应用）

前言

之前我们学习了unordered_set和unordered_map的使用，并了解和模拟实现了其地层结构——哈希桶，并对自己实现的哈希桶进行了封装，封装模拟实现了的unordered_set和unordered_map，同时我们了解到，哈希表的查找性能很高时间复杂度为〇（1），所以其思想也得到了广泛的应用，本文我们就来介绍其思想的两个应用 —— 位图和布隆过滤器。

---

1. 位图

在STL官方库中也有位图：

位图使用文档介绍：

1.1 海量数据处理思路分析：

当我们有海量的数据要处理的时候，例如下面的例题：

【腾讯】 给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在
这40亿个数中。

1. 首先我们先来大概的算一下，10亿个Byte（字节）大概是占几个G：

• • 10亿Byte = 10亿 / 1024 KB = 10亿 / 1024 / 1024MB = 10亿 / 1024 / 1024 / 1024G = 0.93G

通过上面的计算我们得到，10亿个字节的数据大概是占1个G，那么40亿个无符号整数，则是占16个G的内存。

2. 我们能否通过之前学的容器将这么多的数据存储进去：

• 很显然这更不可能，原因也很简单
• • 以红黑树为例，每存4个Byte还要有4个Byte的消耗（颜色 + 三叉链）
• • 哈希表也是类似的道理，但是比红黑树消耗小一点

3. 我们能否通过排序的方式：

• 首先一点内排序肯定是不行的，数据量太大了
• 通过外排序 + 二分查找的方式（也是不可以的）
• • 16G可以开出来，但是连续的16G就开不出来
• • 文件不能随机读取，只能挨个挨个读取，所以是不支持二分查找的
• • 同时外排序的话消耗也很大，这里的数据量也非常大

4. 直接定址法哈希 —— 用一个比特位标识映射值在不在：

• 既然这么多数据我们存不了，我们的目的是判断其在不在这40亿个数据中
• 我们只需要标识一下该数字在不在就可以，这里采用用一个比特位标识
• 比特位是1就表示其在，比特位是0就表示其不在
• • 那么我们知道无符号整数最大就是4,294,967,295，我们只需要给0 ~ 4,294,967,295个比特位
• • 就能将所有的无符号整数的范围都包含在内
• • 接下来直接哈希映射，直接定址法映射

注意：

• 这里开的是42亿九千万个（整形最大值个）比特位，而不知题目中的40亿个
• 因为开的是范围，而不是个数
• 用一个比特位标识的原因
• • 用一个比特位只能有两个值，正好表示两种状态
• • 如果用一个int来标识的话，那么一个int能标识256种状态

这就是用位图的方式来解决该问题。

---

1.2 位图的具体实现：

位图如何开空间：

因为我们开的是比特位的整数个，但是又没有直接精确控制到比特位个数的开空间方法，所以采用一下方式：

位图如何插入标识位：

这里的插入并不是直接将数据插入到位图中，而是将数据对应的哈希地址所在的比特位标识成1。

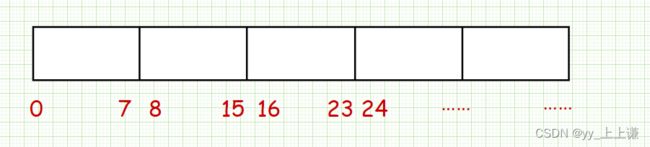
• 因为我们用的是char为一个vector的数据类型，所以我们先定位在哪一个char中
• 例如：18，我们先定位它在哪一个char中，所以我们18 / 8，先定好位
• 再用18 % 8定位其具体在这个char中的哪一个比特位

如何实现插入？

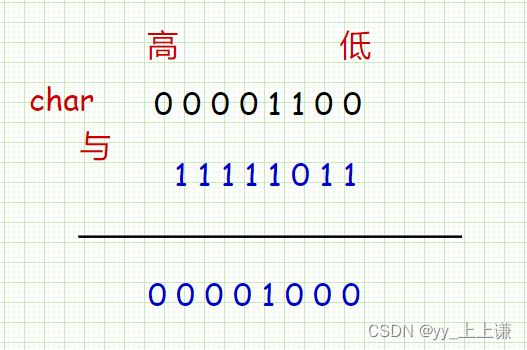
我们想到了或运算和位运算：

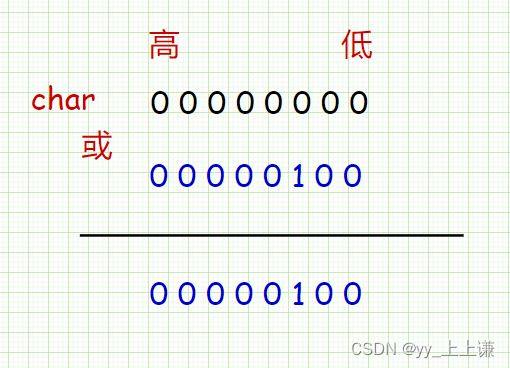
只需要将1左移要标记的位之后与原来的数或一下，就成功标记好了。

如何实现删除：

• 同样的道理我们先定位到要删除的那个位置通过：/、%操作
• 只需要将1左移要标记的位置之后，先取反，再与一下

如何实现查找：

• 只需要将1左移要标记的位置之后，直接与所在的char所表示的整数值与一下即可

通过任务管理器来查看内存

由图也就验证了开了四十二亿个比特位，大概是五百多MB。

具体代码：

//位图既节省空间又快。〇（1）就能判断
//N个比特位的位图  10  16
template<size_t N>//非类型模板参数
class bitset
{
public:
	bitset()
	{
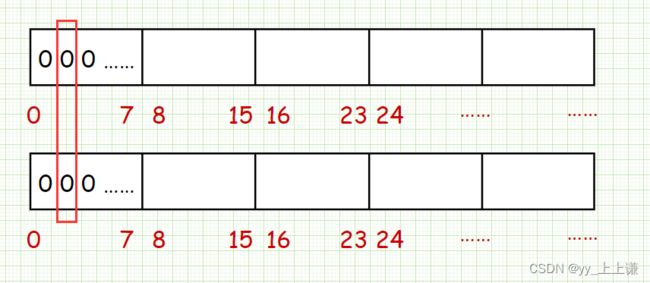
		//+1保证足够比特位，最多浪费8个
		_bits.resize(N / 8 + 1, 0);
	}

	//x映射的位标记成1
	void set(size_t x)
	{
		//x映射的比特位在第几个char对象
		size_t i = x / 8;

		//x在char第几个比特位
		size_t j = x % 8;

		_bits[i] |= (1 << j);
	}

	void reset(size_t x)
	{
		//x映射的比特位在第几个char对象
		size_t i = x / 8;

		//x在char第几个比特位
		size_t j = x % 8;

		//! && ||
		//~ &  | 
		_bits[i] &= (~(1 << j));//不管原来的位置是1还是0，都要搞成0
	}

	//判断x在不在，是1返回true，是0返回false
	bool test(size_t x)
	{
		//x映射的比特位在第几个char对象
		size_t i = x / 8;

		//x在char第几个比特位
		size_t j = x % 8;
		
		return _bits[i] & (1 << j);
	}

private:
	std::vector<char> _bits;
	//vector _bits;
};

位图的应用

1. 快速查找某个数据是否在一个集合中
2. 排序 + 去重
3. 求两个集合的交集、并集等
4. 操作系统中磁盘块标记

---

1.3 用位图解决问题：

应用一：

1. 给定100亿个整数，设计算法找到只出现一次的整数。

• 我们知道无符号整数最多也就四十多亿个，100亿个必然有大量重复的。
• 我们来计算一下100亿个整数是多大，100亿个整数就是400亿个字节，那么大概就是40G的大小。

很显然用之前学的容器内存是放不下40G这么大的数据的，那我们如何用位图来解决？

• 先来分析一下，该用几个为来标识
• 分类一下：出现0次，出现1次，出现两次及以上的
• 那我们此时就要用两个比特位来标识
• 那我们是对之前的位图进行修改吗，这里我们并没有，而是直接复用两个位图

每个位图还是原来的大小（四十二亿九千万个），因为计算机表示的整数也就4,294,967,295个，其余的也都是重复。

• 我们知道100亿个整数的范围肯定是在0 ~ 4,294,967,295之间的，所以我们开两个位图，重复的数对应的位置在每个表中是一样的。

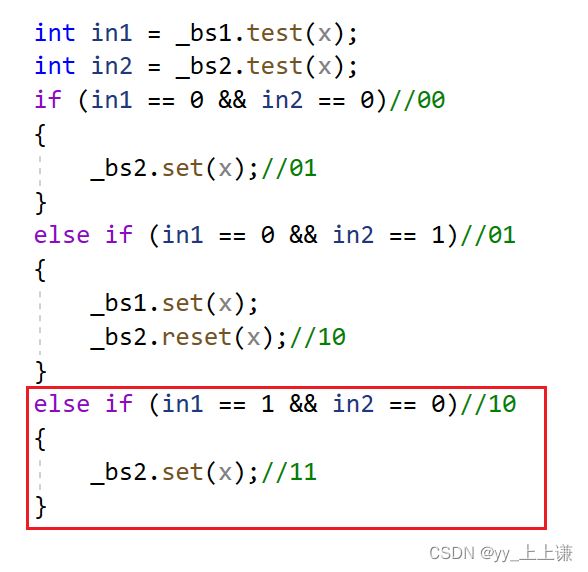
• 此时我们就需要标识：00（一次都没出现的），01（只出现一次的），其他（出现两次及以上的）

template<size_t N>
class two_bitset
{
public:
	void set(size_t x)
	{
		int in1 = _bs1.test(x);
		int in2 = _bs2.test(x);
		if (in1 == 0 && in2 == 0)
		{
			_bs2.set(x);
		}
		else if (in1 == 0 && in2 == 1)
		{
			_bs1.set(x);
			_bs2.reset(x);
		}
	}

	bool is_once(size_t x)
	{
		return _bs1.test(x) == 0 && _bs2.test(x) == 1;
	}

private:
	//开两个位图复用前面操作
	bitset<N> _bs1;
	bitset<N> _bs2;
};

应用二：

2. 给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

因为只给了1个G的内存，我们首先想到的是用到两个位图，正好1个G。

解决办法：

• 在找交集之前我们一定要先做的是去重，对每个文件都要去重，不然就会找到重复交集。
• • 方法一：分别将两个文件映射到两个位图中，挨个挨个比，利用对应算法找两个去重之后位图的交集
• • 方法二：分别将两个文件映射到两个位图中，直接将两个位图与一下，剩下的就是交集了

应用三：

3. 位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数。

• 这题和应用一是一样的，只是多记录和判断了一次，因为不超过2次有：0、1、2。
• 分类一下：出现0次，出现1次，出现2次，出现两次以上的
• 同样是复用了两个位图
  

---

2. 布隆过滤器

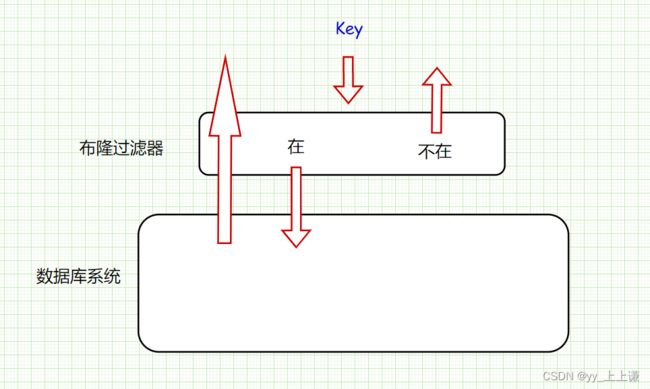
在之前我们讲到了位图，他能迅速判断一个数是否在海量数据中。位图是直接映射，也不存在哈希冲突，空间消耗几乎没有，并且快，直接是O(1)，但是位图只是适合于整形的查找，并不适用于浮点数字符串甚至是一些自定义类型的查找。

2.1 布隆过滤器的概念：

布隆过滤器是由 布隆（Burton Howard Bloom） 在1970年提出的一种紧凑型的、比较巧妙的概率型数据结构，特点是高效地插入和查询，可以用来告诉你 “某样东西一定不存在或者可能存在”，它是用个哈希函数，将一个数据映射到位图结构中。此种方式不仅可以提升查询效率，也可以节省大量的内存空间。

比如说是10亿个字符串是否在一个文件中。

我们来判断一下能否用红黑树哈希表来存储这10亿个字符串呢？

• 这肯定是不能的，因为10个Byte就是1G
• 假设每个字符串是10个Byte，那么光这么多字符串就已经占了十几个G了
• 还有红黑树和哈希表自带的消耗，那几十个G就没了，所以肯定不行

此时一个叫布隆的人，正如概念中所提到的运用了位图的思想，将字符串转化成一个整数，然后映射到位图当中。

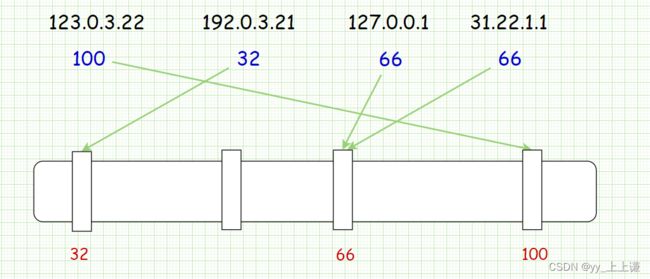
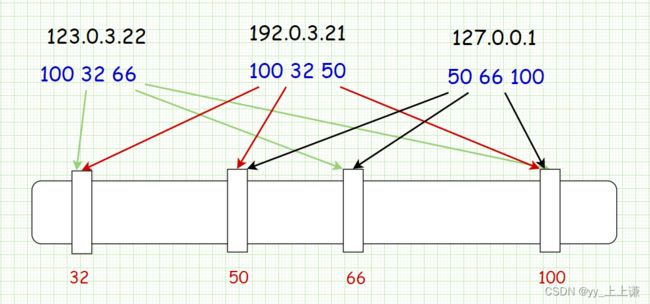
如图我们给出一组ip：

• 我们运用哈希表中学的将字符串转成整数，在将转化成的整数映射到位图中。
• 但是布隆过滤器是无法解决哈希冲突的
• • 首先映射到的是位图中，那么挂桶肯定是不行的，比特位挂不住桶
• • 其次线性探测 / 二次探测也是不行的，因为在哈希表中可以对比数据，但是在位图中比不了，因为每个比特位仅仅是个标识位，并不是能比较
• • 在：有可能是重复了的之前映射过了，又来了一个同样的字符串判段其在，或者是其他字符串通过哈希函数的转换之后，映射到了之前标记在的地方，造成了误判
• • 不在：之前没有对应的字符串映射到为图中对应的位置，判断不在是准确的
• • 所以字符串转整形必然会出现哈希冲突（因为字符串无限多），并且是解决不了的。

既然哈希冲突解决不了，那么我们就降低冲突的概率，降低误判：

布隆过滤器采用的是一个字符串映射多个值，在判断在不在时，当着多个值都存在的时候，才能判断其存在，不然就是不在。

• 有人就专门研究并统计了，误判率影响的因素
• 误判率影响的因素研究统计报告

我们截取一下公式：

通过上述公式，我们哈希函数个数k取3得到：

4.35 * n = m

也就是说在3个哈希函数的时候，没插入一个元素，就需要5个比特位来标识。

布隆过滤器是复用位图的：

struct BKDRHash
{
	size_t operator()(const string& s)
	{
		//BKDR
		size_t value = 0;
		for (auto ch : s)
		{
			value *= 31;
			value += ch;
		}
		return value;
	}
};

struct APHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 0;
		for (long i = 0; i < s.size(); i++)
		{
			if ((i & 1) == 0)
			{
				hash ^= ((hash << 7) ^ s[i] ^ (hash >> 3));
			}
			else
			{
				hash ^= (~((hash << 11) ^ s[i] ^ (hash >> 5)));
			}
		}
		return hash;
	}
};

struct DJBHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 5381;
		for (auto ch : s)
		{
			hash += (hash << 5) + ch;
		}
		return hash;
	}
};

struct JSHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 1315423911;
		for (auto ch : s)
		{
			hash ^= ((hash << 5) + ch + (hash >> 2));
		}
		return hash;
	}
};

template<size_t M,
	class K = string,
	class HashFunc1 = BKDRHash,
	class HashFunc2 = APHash,
	class HashFunc3 = DJBHash,
	class HashFunc4 = JSHash>
class BloomFilter
{
public:
	void Set(const K& key)
	{
		size_t hash1 = HashFunc1()(key) % M;
		size_t hash2 = HashFunc2()(key) % M;
		size_t hash3 = HashFunc3()(key) % M;
		size_t hash4 = HashFunc4()(key) % M;

		//cout << hash1 << " " << hash2 << " " << hash3 << endl;

		_bs.set(hash1);
		_bs.set(hash2);
		_bs.set(hash3);
		_bs.set(hash4);
	}

	bool Test(const K& key)
	{
		size_t hash1 = HashFunc1()(key) % M;
		if (_bs.test(hash1) == false)
		{
			return false;
		}

		size_t hash2 = HashFunc2()(key) % M;
		if (_bs.test(hash2) == false)
		{
			return false;
		}

		size_t hash3 = HashFunc3()(key) % M;
		if (_bs.test(hash3) == false)
		{
			return false;
		}

		size_t hash4 = HashFunc4()(key) % M;
		if (_bs.test(hash4) == false)
		{
			return false;
		}

		return true; //存在误判
	}

	//布隆过滤器的删除可能会影响别的数据存储情况，所以不支持直接删除 -- 需要付出代价的
	bool Reset(const K& key);

private:
	bitset<M> _bs;
};

2.2 布隆过滤器的测试：

测试1

void TestBloomFilter1()
{
	//插入10个值
	//BloomFilter<60, string, BKDRHash, APHash, DJBHash> bf;
	BloomFilter<60> bf;

	string a[] = { "苹果", "香蕉", "西瓜", "111111111", "eeeeeffff", "草莓", "休息", "继续", "查找", "set" };

	for (auto& e : a)
	{
		bf.Set(e);
	}

	for (auto& e : a)
	{
		cout << bf.Test(e) << " ";
	}

	cout << endl;

	cout << bf.Test("芒果") << " ";
	cout << bf.Test("string") << " ";
	cout << bf.Test("ffffeeeee") << " ";
	cout << bf.Test("31341231") << " ";
	cout << bf.Test("ddddd") << " ";
	cout << bf.Test("3333343") << " ";
}

我们提供了四个哈希函数，那么每插入一个数据就差不多需要60个比特位。

测试2：

void TestBloomFilter2()
{
	srand(time(0));
	const size_t N = 1000;//<>内放的是常量
	BloomFilter<6 * N> bf;

	std::vector<std::string> v1;
	std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";

	for (size_t i = 0; i < N; i++)
	{
		v1.push_back(url + std::to_string(1234 + i));
	}

	for (auto& str : v1)
	{
		bf.Set(str);
	}

	std::vector<std::string> v2;
	for (size_t i = 0; i < N; ++i)
	{
		std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";
		url += std::to_string(999999 + i);
		v2.push_back(url);
	}

	size_t n2 = 0;
	for (auto& str : v2)
	{
		if (bf.Test(str))
		{
			n2++;
		}
	}
	cout << "相似字符串误判率:" << (double)n2 / (double)N << endl;

	std::vector<std::string> v3;
	for (size_t i = 0; i < N; ++i)
	{
		string url = "zhihu.com";
		url += std::to_string(rand());
		v3.push_back(url);
	}

	size_t n3 = 0;
	for (auto& str : v3)
	{
		if (bf.Test(str))
		{
			n3++;
		}
	}
	cout << "不相似字符串误判率:" << (double)n3 / (double)N << endl;
}

我们分别对相似字符串和不相似字符串的误判率进行测试：

测试可见：布隆过滤器开的越大，误判率就越低。

2.3 布隆过滤器的删除：

因为布隆过滤器采用的是多组映射的方式，所以要是直接删除的话可能会影响其他的值存不存在的标识，所以布隆过滤器的删除是不能直接删除的。

布隆过滤器可以删除，但是要付出代价：

• 通过计数删除，映射一个值就在位图的标记位上计数
• 用到该位置就++，显然标识位不能再用比特位了
• • 1bit标识一个位置
• • 8bit标识一个位置 0 ~ 255
• • 16bit标识一个位置 0 ~ 65535
• 还有溢出的风险

一个数删除之后，判断还在，说明是误判了。

此种方法的缺陷：

1.无法确认元素是否真正在布隆过滤器中
2.存在计数回绕

布隆过滤器优点:

1.增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数，一般比较小)，与数据量大小无关
2.哈希函数相互之间没有关系，方便硬件并行运算
3.布隆过滤器不需要存储元素本身，在某些对保密要求比较严格的场合有很大优势
4.在能够承受一定的误判时，布隆过滤器比其他数据结构有这很大的空间优势
5.数据量很大时，布隆过滤器可以表示全集，其他数据结构不能
6.使用同一组散列函数的布隆过滤器可以进行交、并、差运算

布隆过滤器缺陷：

1.有误判率，即存在假阳性(False Position)，即不能准确判断元素是否在集合中(补救方法：再建立一个白名单，存储可能会误判的数据)
2.不能获取元素本身
3.一般情况下不能从布隆过滤器中删除元素
4.如果采用计数方式删除，可能会存在计数回绕问题

2.4 布隆过滤器的应用：

1.注册的时候，快速判断一个昵称是否使用过：

• 将系统所有的昵称都映射到布隆过滤器中
• 不在：说明没人有用过
• 在：再去数据库查确认一遍（因为在的话存在误判）

2.黑名单：

• 不在：通行
• 在：再次去系统确认（绝不放过一个坏人，但有可能误抓好人）

3.过滤层，提高查找数据效率：

---

3. 哈希切割（只提及思想）

哈希切割：

• 给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？
• 与上题条件相同，如何找到top K的IP？

问题：

• 位图和布隆是Key的模型，无法解决Key_ Value的模型
• 只能哈希表和红黑树，但是内存又不够

解决方案一：

• 如何统计次数，很显然100G的log中的IP肯定是不能放在红黑树或者哈希表中的。
• 这里我们采用将文件分割，假设将每个文件分成100份，每个文件就是1G就可以放在红黑树或者哈希表中了。
• 不过这里是存在问题的
• • 会存在大量相同的IP会被分到不同的文件当中
• • 如果要想统计个数，那么最后要合并还是会存在放不下的问题

解决方案二：

• 综合方案一的问题，我们就要将相同的IP放在同一个文件当中

然后再用红黑树和哈希表来统计：

TopK复习： 传送门

注意：

• 不同的ip也有可能进入同一个文件，但是相同的ip一定是进入同一个文件。

存在问题：

• 某个文件太大了，哈希表和红黑树中放不下

• • a. 某个相同的ip太多 - 这时候存储大概率是够的，因为相同的ip存在map中只是统计次数，不额外占用空间。
• • b. 映射冲突到这个编号文件的ip太多 - 但是冲突的太多的话，还是会大量文件存在小文件中，依旧会存在一个小文件太大的情况。
• • 解决办法：是针对小文件再分割，再用其他哈希函数，进行哈希分割，再切分成小文件。

• 大量相同时，都集中在一个小文件，再去切分是不起作用的，切分完之后还是在同一个文件里
• a不会抛异常(大量相同的ip) ，b会抛异常(大量冲突不同的ip)

布隆过滤器找交集：

给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？分别给出精确算法和近似算法。

假设每个query平均30byte，100亿query就是300G。

似算法：

• 将一个文件映射到布隆过滤器中，用另一个文件去找，利用布隆过滤器的快速性，不过可能存在误判的问题。
• 所以这叫不精确的，近似算法。

精确算法：

• 方法： 相同的小文件找交集，对应编号找交集

• 通过哈希分割，A、B文件中相同的数据肯定被分到了相同的小文件
• 对小文件找交集，那么就很容易了，用set就可以很快找到