克里金(kriging)模型的推导详解
Kriging模型理论推导
- 1、前言
- 2、条件
- 3、基础知识
-
-
- 3.1、方差的理解
- 3.2、概率密度函数
- 3.3、多元正态分布
-
- 4、理论推导
-
-
- 4.1 模型建立
- 4.2 模型预测
-
1、前言
简介:Kriging模型是一种通过已知试验点信息来预测未知试验点上响应的无偏估计模型,其最早是由南非矿业工程师D.G.Krige于1951年提出。20世纪70年代,法国的数学家G.Matheron对D.G.Krige的研宄成果进行了进一步的系统化、理论化,并将其命名为Kriging模型。1989年Sacks等将Kriging模型推广至试验设计领域,形成了基于计算机仿真和Kriging模型的计算机试验设计与分析方法。
本文将从原理部分,解析Kriging模型的推导过程。本次克里金模型的推导的参考文献为:
A Taxonomy of Global Optimization Methods Based on Response Surfaces。
2、条件
克里金模型在应用时有如下假设条件:
(1)、克里金法假设所有数据之间都服从n维的正态分布。
(2)、无偏。
3、基础知识
在推导克里金模型之前,先来回顾一些统计学的基础知识,各位功底深厚的看客老爷可以直接跳过。
3.1、方差的理解
概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。机器学习中方差又可以理解为不确定性的一种,即方差越大,不确定性越大。
3.2、概率密度函数
在数学中,连续型随机变量的概率密度函数是描述这个随机变量的输出值,在某个确定的取值点附近的可能性的函数。而随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分。当概率密度函数存在的时候,累积分布函数是概率密度函数的积分。
3.3、多元正态分布
平常我们见的最多的正态分布大多是是一维的,其的概率密度函数(Probability density function,PDF)如下:
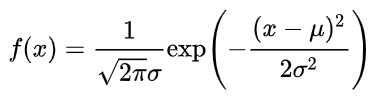
其中,μ为均值,σ2为方差。也就是说,在均值和方差确定的条件下,上式f(x)也就确定了,这样我们就可以知道在该分布下,随机变量x的可能性大小。
同样,当拓展到二维正态分布时,相当于添加了一个维度,这是均值仍然为每个维度上的均值组合到一起,而方差则变为了协方差,因为要考虑这两个维度之间的关系。此时的均值和协方差变为:
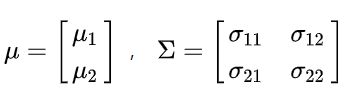
此时二元正态分布的概率密度函数(pdf)为:

其中ρ为相关系数,是由这两个维度上的方差计算得到的,如下图所示:x是第一维度上的随机变量,在该维度上,x服从正态分布,同样的,y是第二维度上的随机变量,在该维度上,同样服从正态分布。z就是随机变量x和y取某一个确定值的可能性大小。

以上为二元正态分布,多元正态分布也是类似,在增加维度即可,不过当维度超过2时,就无法可视化,但并不妨碍我们理解。
多元正态分布的均值向量为:
![]()
多元正态分布的协方差矩阵为:

其分布函数为:

也就是说,如果多元正态分布的均值确定了,协方差确定了,那么其分布函数(pdf)就可以确定,我们就可以在这个分布函数上搞点儿事情。比如进一步的进行最大似然估计。
4、理论推导
4.1 模型建立
已知给定了一些标记过的数据集X = { x1,x2,…,xn },其对应的目标函数值为y = { y1,y2,…,yn } ,注意,其中的 x1 是一个长度为 n 的向量,y1 = Y(x1) 。我们的目标就是想通过这些已知的点,来实现对未知点的预测。
首先,克里金模型假设所有数据服从均值为μ方差为σ2的n元的正态分布,也就是说这个n元正态分布函数的均值可以认为是在[ μ-3σ, μ+3σ ]的范围内变化(论文原话,实际上刻画的是不确定性)。现在我们考虑两个点 xi 和 xj ,在我们采样之前,是不确定这两个点的目标函数值的,然而,我们假设建模所用的函数是连续的,当距离 || xi-xj || 比较小时,y(xi)和y(xj)也倾向于高度相关。我们可以通过下面的式子来衡量相关性:

上面是论文中的描述,初学者可能会比较蒙,下面我简单解释一下:
既然克里金模型假设了所有数据服从n维正态分布,那么对于n维的正态分布,如果想要刻画其pdf,最重要的就是均值和协方差了了,由于是n维,均值为各个维度的均值的组合,为nx1的矩阵,而协方差矩阵里面,非对角线上的元素就是两两随机变量之间的协方差,对角线上的元素就是各个随机变量的方差,(如下图示例,cov(z,x)刻画的是变量z和变量x之间的相关性)。论文中的式(5),就是一个刻画随机变量Y(xi)和变量Y(xj)之间的相关性的函数,属于协方差矩阵中的一员。我们令i=j,那么corr[Y(xi),Y(xj)]就为1.
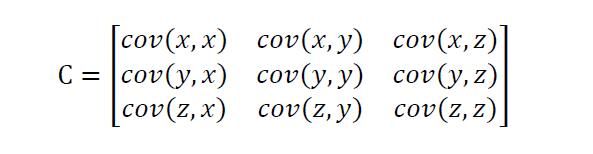
紧接着,由于Y是服从n元正态分布,我们将n个已知点放到一起,就变成了:

Y的均值为lμ,其中l是nx1的矩阵。其协方差如下:
![]()
注意:文献中得R乘以了方差,文献作者应该是想表示协方差矩阵对角线上的值,不过不妨碍我们理解,这里我补充出Cov(Y)的表达式,见下图:
( C o r r [ Y ( X 1 , X 1 ) ] . . . C o r r [ Y ( X 1 , X n ) ] . . . . . . . . . C o r r [ Y ( X n , X 1 ) ] . . . C o r r [ Y ( X n , X n ) ] ) \begin{pmatrix} Corr[Y(X1,X1)]&...&Corr[Y(X1,Xn)]\\ ...&...&...\\ Corr[Y(Xn,X1)]&...&Corr[Y(Xn,Xn)]\\ \end{pmatrix} ⎝⎛Corr[Y(X1,X1)]...Corr[Y(Xn,X1)].........Corr[Y(X1,Xn)]...Corr[Y(Xn,Xn)]⎠⎞
上式中的对角线上的值就是向量各自的方差。
这里的R的大小为n x n的矩阵,该矩阵中的每个值都是由公式(5)得到的,i和j都是从1取到n。对角线上i=j,所以R为1,那么协方差Cov(Y)的对角线就是方差。
由上公式可知超参数有μ、σ2,θl和pl(l=1,2,3…d),我们用观测数据y进行最大化似然来估计这些超参数,观测数据y如下所示:

由于服从多维正态分布,最大似然的式子可以写为:

为了方便运算,取对数:
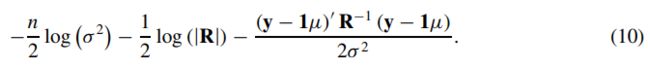
下面分别对均值μ、和方差σ2求偏导,即可得到使似然函数最大的均值和方差了,得到结果如下:
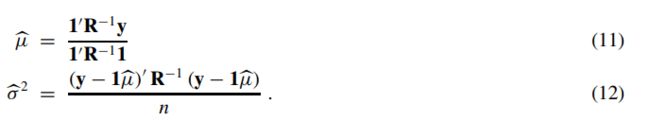
最后,将公式(11)和(12)带入到式(10)中得到log最大似然为:

由式13可知,log最大似然仅和R有关,而R中有参数θ,因此超参数的调节就是选取合适的θ使得log似然最大,可以用遗传算法或多初始点算法求得。
4.2 模型预测
在4.1中,我们对已知得数据点进行了最大似然估计,得到一些先验超参数,预测就是利用4.1得到得超参数来对未知数据点进行预测。这里考虑一个点 y ~ \widetilde{y} y ,我们将观察到的数据和要预测的点放到一起 y ~ \widetilde{y} y =(y’,y*)T ,则对应的协方差矩阵也发生了改变:

则协方差矩阵变为:

矩阵中得 r’ 实际是 rT 的意思。则对应的似然函数为:
**式(10)**在加上下面图片中的式子:
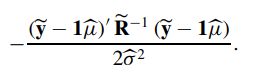
将 y ~ \widetilde{y} y 和 R ~ \widetilde{R} R 带入到上式中得:

下面要做的是如何把中间的逆矩阵表示出来,这里作者用了部分求逆的方法,直接上结果如下:
R ~ \widetilde{R} R -1 =

将上式带入到式(16)中,我们可以得到扩充后的似然函数为:
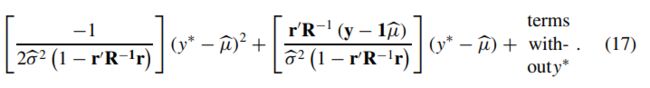
我们可以看到,式(17)是关于y*的二次函数,对其求导并等于0可得:

从式(18)可以求解出:y*= y ^ \widehat{y} y (x*) = μ ^ \widehat{μ} μ + r,R-1(y-l μ ^ \widehat{μ} μ )

至此,证明完毕。
本文参考:
(1) https://zhuanlan.zhihu.com/p/90272131
(2) 文献:A Taxonomy of Global Optimization Methods Based on Response Surfaces