【蓝桥杯冲刺】蓝桥杯12届省赛C++b组真题-编程题
目录
试题F:时间显示
解题思路
代码
试题G:砝码称重
解题思路
代码
试题H:杨辉三角
解题思路
代码
试题I:双向排序
解题思路
试题J:括号序列
解题思路
试题F:时间显示
【问题描述】
小蓝要和朋友合作开发一个时间显示的网站。
在服务器上,朋友已经获取了当前的时间,用一个整数表示,
值为从 1970 年 1 月 1 日 00 : 00 : 00 到当前时刻经过的毫秒数。
现在,小蓝要在客户端显示出这个时间。
小蓝不用显示出年月日,只需显示出时分秒即可,毫秒也不用显示,直接舍去即可。
给定一个用整数表示的时间,请将这个时间对应的时分秒输出。
【输入格式】
输入一行包含一个整数,表示时间。
【输出格式】
输出时分秒表示的当前时间,格式形如 H H:M M:S S ,
其中 H H 表示时,值为 0 到 23,
M M 表示分,值为 0 到 59,
S S 表示秒,值为 0 到 59 。
时、分、秒不足两位时补前导 0 。
【测试样例1】
Input:
46800999
Output:
13:00:00
【测试样例2】
Input:
1618708103123
Output:
01:08:23
【评测用例规模与约定】
对于所有评测用例,给定的时间为不超过10的18次方的正整数。
解题思路
这是一道简单的模拟题,
根据题目给的毫秒数,求出当前的时间就行。
代码
#include
using namespace std;
int main() {
long long t;
cin >> t;
int h = t / 1000 / 60 / 60 % 24;
int m = t / 1000 / 60 % 60;
int s = t / 1000 % 60;
printf("%02d:%02d:%02d", h, m, s);
return 0;
} 试题G:砝码称重
【问题描述】
你有一架天平和 N 个砝码,
这 N 个砝码重量依次是 W1 , W2 , ⋅ ⋅ ⋅ , WN 。
请你计算一共可以称出多少种不同的重量?
注意砝码可以放在天平两边。
【输入格式】
你有一架天平和 N 个砝码,这 N 个砝码重量依次是 W1 , W2 , ⋅ ⋅ ⋅ , WN 。
【输出格式】
输出一个整数代表答案。
【测试样例1】
Input:
3
1 4 6
Output:
10
Explanation:
能称出的 10 种重量是:1、2、3、4、5、6、7、9、10、11。
1 = 1;
2 = 6 − 4 (天平一边放 6,另一边放 4);
3 = 4 − 1;
4 = 4;
5 = 6 − 1;
6 = 6;
7 = 1 + 6;
9 = 4 + 6 − 1;
10 = 4 + 6;
11 = 1 + 4 + 6。
【评测用例规模与约定】
对于 50% 的评测用例,1 ≤ N ≤ 15 。
对于所有评测用例,1 ≤ N ≤ 100 ,N 个砝码总重不超过 100000 。
解题思路
这是一道动态规划题目啊,
但是我不会动态规划,所以我就只能写个暴力搜索,
下面是代码:(只能过50%用例)
代码
#include
using namespace std;
int n, res;
int w[10000];
bool st[10000];
void dfs(int x, int sum) {
if (x == n) {
//有重量且该重量没被标记过
if (!st[sum] && sum > 0) {
st[sum] = true;
res++;
return;
}
}
else {
dfs(x + 1, sum + w[x]);//放左边
dfs(x + 1, sum); //不放
dfs(x + 1, sum - w[x]);//放右边
}
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &w[i]);
dfs(0, 0);
printf("%d\n", res);
return 0;
} 试题H:杨辉三角
【问题描述】
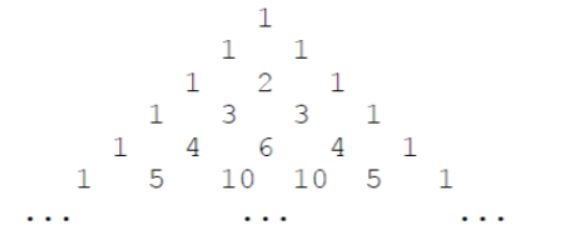
下面的图形是著名的杨辉三角形:
如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如下数列:
如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如下数列:
1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, ...
给定一个正整数 N,请你输出数列中第一次出现 N 是在第几个数?
【输入格式】
输入一个整数 N。
【输出格式】
输出一个整数代表答案。
【测试样例1】
Input:
6
Output:
13
【评测用例规模与约定】
对于 20% 的评测用例,1 ≤ N ≤ 10;
对于所有评测用例,1 ≤ N ≤ 1e9 。
解题思路
菜鸟做不出来,
只能暴力枚举1000个数构造杨辉三角。
(只拿40%左右的分数)
代码
#include
using namespace std;
const int N = 1010;
int n = 1000;
int x;
int a[N][N];
int main() {
scanf("%d", &x);
a[1][1] = 1;
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= i; j++) {
a[i][j] = a[i - 1][j - 1] + a[i - 1][j];
}
}
int cnt = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
cnt++;
if (a[i][j] == x) {
cout << cnt << endl;
return 0;
}
}
}
return 0;
} 试题I:双向排序
【问题描述】
给定序列 (a1, a2, ⋅⋅⋅, an) = (1, 2,⋅⋅⋅, n),即 ai = i 。
小蓝将对这个序列进行 m 次操作,
每次可能是将 a1 , a2 , ⋅⋅⋅ , aqi 降序排列,或者将 aqi, aqi + 1 升序排列。
请求出操作完成后的序列。
【输入格式】
输入的第一行包含两个整数 n, m,分别表示序列的长度和操作次数。
接下来 m 行描述对序列的操作,其中第 i 行包含两个整数 pi, qi 表示操作类型和参数。
当 pi = 0 时,表示将 a1, a2,⋅⋅⋅,aqi 降序排列;当 pi = 1时,表示将 aqi, aqi + 1,⋅⋅⋅ , an 升序排列。
【输出格式】
输出一行,包含 n 个整数,相邻的整数之间使用一个空格分隔,表示操作完成后的序列。
【测试样例1】
Input:
3 3
0 3
1 2
0 2
Output:
3 1 2【评测用例规模与约定】
对于 30%30% 的评测用例,n,m≤1000;
对于 60%60% 的评测用例,n,m≤5000;
对于所有评测用例,1 ≤ n, m ≤ 1e5,0 ≤ pi ≤ 1,1 ≤ qi ≤ n1 。
解题思路
太难了,我写不出来。。。。
试题J:括号序列
解题思路
别看啦,这题我更做不出来了。。。呜呜。。。
写在最后:
以上就是本篇文章的内容了,感谢你的阅读。
如果喜欢本文的话,欢迎点赞和评论,写下你的见解。
如果想和我一起学习编程,不妨点个关注,我们一起学习,一同成长。
之后我还会输出更多高质量内容,欢迎收看。