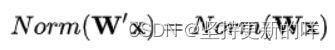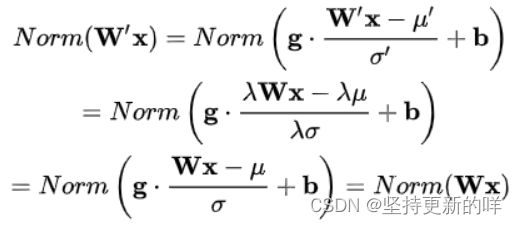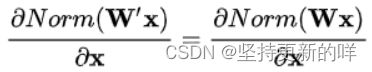BatchNorm和LayerNorm

目录

独立同分布（independent and identically distributed）与白化

ICS（Internal Covariate Shift内部协变量偏移）

Batch Normalization 

Layer Normalization

BN vs LN

主流Normalization方法为什么有效？

---

独立同分布（independent and identically distributed）与白化

→为什么独立同分布？

独立同分布的数据可以简化常规机器学习模型的训练、提升机器学习模型的预测能力。

→相关性：

强相关：Naive Bayes（朴素贝叶斯）模型就建立在特征彼此独立的基础之上。

弱相关：Logistic Regression和神经网络则在非独立的特征数据上依然可以训练出很好的模型。

→白化

作用：去除特征间的相关性→独立；使所有特征具有相同的均值和方差：同分布

ICS（Internal Covariate Shift内部协变量偏移）

动机：深度神经网络涉及到很多层的叠加，而每一层的参数更新会导致上层的输入数据分布发生变化，通过层层叠加，高层的输入分布变化会非常剧烈，这就使得高层需要不断去重新适应底层的参数更新。为了训练好模型，我们需要非常谨慎地去设定学习率、初始化权重、以及尽可能细致的参数更新层略。

模型训练对于一个数据的假设：“源空间（source domain）和目标空间（target domain）的数据分布（distribution）是一致的”。如果不一致，那么就出现了新的机器学习问题，如transfer learning/domain adaptation等。而covariate shift 就是分布不一致假设下的一个分支问题，它是指源空间和目标空间的条件概率是一致的，但是其边缘概率不同。

→ICS[每个神经元的输入数据不再是“独立同分布”]导致的后果：

上层参数需要不断适应新的输入数据分布，降低学习速度；

下层输入的变化可能趋向于变大或者变小，导致上层落入饱和区，使得学习过早停止；

每层的更新都会影响到其他层，因此每层的参数更新策略需要尽可能的谨慎。

ICS问题带来的后果是什么？

上层参数需要不断适应新的输入数据分布，降低学习速度；

下层输入的变化可能趋向于变大或者变小，导致上层落入饱和区，使得学习过早停止；

每层的更新都会影响到其他层，因此每层的参数更新策略需要尽可能的谨慎。

Normalization的通用框架与基本思想

前言：

    假设神经元的输入：x = （x1, x2, ... , xd）

    输出的结果：y = f（x）

ICS问题：x的分布可能相差很大

解决方法：

    方法：对每一层的数据做白化操作

    存在问题：成本高，因为要保证白化操作是可微的

基本思想：

    在将x送给神经元之前，现对其做平移和伸缩变换，将x的分布规范化成在固定区间范围的标准分布。

变换框架：参数介绍：μ：平移参数；：缩放参数

    步骤：1、对x进行shift和scale变换，得到的数据符合均值为0、方差为1的标准分布。

    2、b是再平移参数（re-shift parameter），g是再缩放参数（re-scale parameter）,再进一步变换为下面的式子，得到的数据符合均值为b，方差为的分布。

Batch Normalization 

Batch Normalization是什么？

方式：针对单个神经元进行，利用网络训练时一个mini-batch的数据来计算该神经元xi的均值和方差，因而称为Batch Normalization。

Batch Normalization（纵向规范化）存在什么问题？   

BN独立地规范化每一个输入维度xi，但规范化的参数是一个mini-batch的一阶统计量和二阶统计量。这就要求每一个mini-batch的统计量是整体估计量的近似估计，或者说每一个mini-batch彼此之间，以及和整体数据，都应该是近似同分布的。分布差距较小的mini-batch可以看做是为规范化操作和模型训练引入了噪声，可以增加模型的鲁棒性；但如果每个mini-batch的原始分布差别很大，那么不同mini-batch的数据将会进行不一样的数据变换，这就增加了模型训练的难度。

由于BN需要再运行过程中统计每个mini-batch的一阶统计量和二阶统计量，因此不适用于动态的网络结构和RNN网络。

Batch Normalization（纵向规范化）适用的场景是什么？

每个mini-batch比较大，数据分布比较接近。在进行训练之前，要做好充分的shuffle，否则效果会差很多。

BatchNorm存在什么问题？

1、BN特别依赖Batch Size；当Batch Size很小的时候，BN的效果就非常不理想了。在很多情况下，Batch Size大不了，因为你GPU的显存不够。所以，通常会有其他比较麻烦的手段去解决这个问题，比如MegDet的CGBN等；

2、BN对处理序列化数据的网络比如RNN是不太适用的；所以，BN的应用领域减少了一半；

3、BN只在训练的时候用，inference的时候不会用到，因为inference的输入不是批量输入。

Layer Normalization

Layer Normalization（横向规范化）是什么？

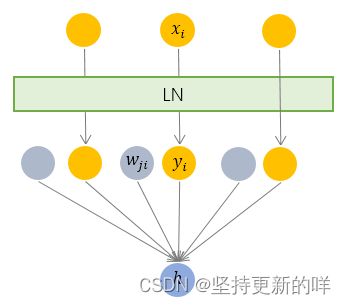
方式：综合考虑一层所有维度的输入，计算该层的平均输入值和输入方差，然后用同一个规范化操作来转换各个维度的输入。其中i枚举了该层所有的输入神经元。对应到标准公式中，四大参数, g, b均为标量（BN中是向量），所有输入共享一个规范化变换。 

Layer Nomalization（横向规范化）有什么作用？

LN针对单个训练样本进行，不依赖于其他数据，因此可以避免BN中受mini-batch数据分布的影响的问题，可以用于小mini-batch场景，动态网络场景和RNN，特别是自然语言处理领域。此外，LN不需要保存mini-batch的均值和方差，节省了额外的存储空间。

BN vs LN

BN的转换是针对单个神经元可训练的——不同神经元的输入经过再平移和再缩放后分布在不同的区间，而LN对于一整层的神经元训练得到同一个转换——所有的输入都在同一个区间范围内。如果不同输入特征不属于相似的类别（比如颜色和大小），那么LN的处理可能会降低模型的表达能力。 

主流Normalization方法为什么有效？

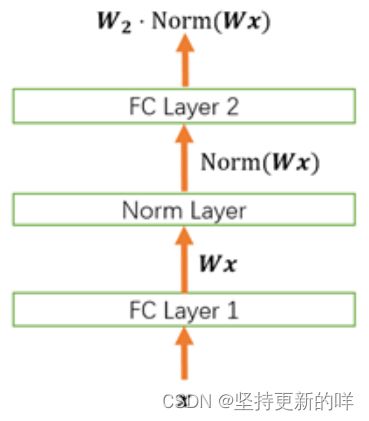
1、Normalization的权重伸缩不变性 

介绍：权重W按照常量进行伸缩时，得到的规范化后的值保持不变。其中。

原因：当权重W伸缩时，对应的权值和标准差均等比例伸缩，分子分母相抵。 

优点：权重伸缩不变形可以有效地提高反向传播的效率。

注：因此，权重的伸缩变化不会影响反向梯度的Jacobian矩阵，因此也就对反向传播没有影响，避免了反向传播时因为权重过大或过小导致的梯度消失或梯度爆炸问题，从而加速了神经网络的训练。

权重伸缩不变性还具有参数正则化的效果，可以使用更高的学习率。

因此，下层的权重值越大，其梯度就越小。这样，参数的变化就越稳定，相当于实现了正则化的效果，避免参数的大幅震荡，提高网络的泛化性能。

2、Normalization的数据伸缩不变性

介绍：当数据x按照常量进行伸缩时，得到的规范化后的值保持不变，注： = 

优点：数据伸缩不变性可以有效地减少梯度弥散，简化对学习率的选择

对于某一层神经元：

可得：

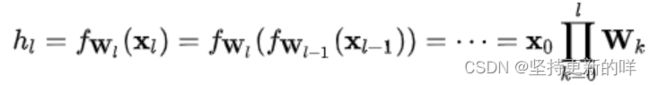每一层神经元的输出依赖于底下各层的计算结果。如果没有正则化，当下层发生伸缩变化时，经过层层传递，可能会导致数据发生剧烈的膨胀或者弥散，从而也导致了反向计算时的梯度爆炸或梯度弥散。

加入Normalization之后，不论底层的额数据如何变化，对于某一层神经元而言，其输入xi永远保持标准的分布，这就使得高层的训练更加简单。从梯度的计算公式来看：

数据的伸缩变化也不会影响到对该层的权重参数更新，使得训练过程更加鲁棒，简化了对学习率的选择。 

前向传播（Forward Propagation）是神经网络中的一种计算方式，用于将输入信号通过网络中的各个层，最终得到网络的输出结果。

在前向传播过程中，输入信号从输入层经过一系列的隐藏层，最终传递到输出层。在每一层中，输入信号通过一组权重矩阵和偏置向量的线性变换，然后经过一个激活函数进行非线性变换，得到该层的输出信号。这个输出信号作为下一层的输入信号，以此类推，直到输出层输出最终的预测结果。

具体来说，前向传播可以分为以下几个步骤：

1. 输入层将输入信号传递给第一个隐藏层
2. 第一个隐藏层通过权重矩阵和偏置向量的线性变换，得到输出信号
3. 输出信号经过激活函数进行非线性变换，得到该层的输出结果
4. 第二个隐藏层重复步骤2-3，以此类推，直到输出层输出最终的预测结果

在前向传播过程中，神经网络中的参数（权重和偏置）保持不变。前向传播只是一个计算过程，用于计算神经网络对于给定输入的输出结果。在训练过程中，我们通常使用反向传播算法来计算梯度，并使用梯度下降等优化算法来更新神经网络的参数，以最小化预测结果与真实结果之间的误差。

反向传播（Backpropagation）是深度学习中用于计算神经网络中每个参数的梯度的一种方法。梯度指的是损失函数对于每个参数的变化率。

在神经网络中，反向传播算法首先通过前向传播来计算出网络的输出结果。然后，它使用链式法则（Chain Rule）来计算每个参数对于损失函数的梯度，从而更新参数以最小化损失函数。具体而言，反向传播算法计算出损失函数关于网络输出的梯度，然后通过链式法则依次计算出每层参数的梯度，最终得到整个网络中每个参数的梯度。

通过反向传播算法计算出的梯度可以用于随机梯度下降等优化算法，以更新神经网络中的参数，从而不断优化网络的预测能力。

梯度下降（Gradient Descent）是一种最小化损失函数的优化算法。在机器学习和深度学习中，通常使用梯度下降算法来更新模型中的参数，以最小化模型预测值与真实值之间的误差。

在梯度下降算法中，我们需要计算损失函数对于模型参数的梯度，即损失函数对于每个参数的变化率。然后，我们使用这些梯度来更新参数，使得损失函数减小。梯度下降的基本思路是：在每一次迭代中，朝着损失函数下降最快的方向更新参数，直到达到损失函数的最小值。

具体来说，梯度下降算法通过以下步骤更新模型参数：

1. 初始化模型参数
2. 在训练集中随机选择一批数据
3. 计算损失函数对于模型参数的梯度
4. 根据梯度和学习率（learning rate）更新模型参数
5. 重复步骤2-4，直到达到指定的迭代次数或损失函数的下降足够小

其中，学习率是梯度下降算法的一个超参数，控制每次更新参数的步长大小。如果学习率过大，可能会导致算法不收敛；如果学习率过小，可能会导致算法收敛速度慢。因此，选择合适的学习率是梯度下降算法的一个重要问题。

参考博客：https://blog.csdn.net/Little_White_9/article/details/123345062?spm=1001.2101.3001.6661.1&utm_medium=distribute.pc_relevant_t0.none-task-blog-2%7Edefault%7EOPENSEARCH%7ERate-1-123345062-blog-129866243.235%5Ev27%5Epc_relevant_recovery_v2&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-2%7Edefault%7EOPENSEARCH%7ERate-1-123345062-blog-129866243.235%5Ev27%5Epc_relevant_recovery_v2&utm_relevant_index=1