实验四-哈夫曼编码的MATLAB实现

信息论编码实验3~9连载，更多看专栏。

一、哈夫曼编码的原理

哈夫曼编码是一种变字长编码，可以使得编码的平均码长很接近信息熵的编码。基本思想就是，出现概率大的符号编码短一点（码长小），出现概率小的符号才用更多的码来表示。

编码步骤：

1. 将所有符号按照出现概率大小降序排列；
2. 从概率最小的两个符号开始，分别配以0和1两种码元（注意顺序会影响编码结果，也可以反过来）。然后将这两个符号概率相加继续和未编码的符号进行码元分配。
3. 按照码元分配顺序，像这样从下往上，直到分配到第一行符号（概率最大，也必然为0）。
4. 最后，从上往下读取编码后的结果，即为哈夫曼编码。

二、哈夫曼编码的实例

正好就按照实验指导书的例题来说吧。
假设有六个符号，符号概率依次为[0.21 0.1 0.3 0.09 0.25 0.05]，要进行哈夫曼编码，先降序排序，结果展示如下：
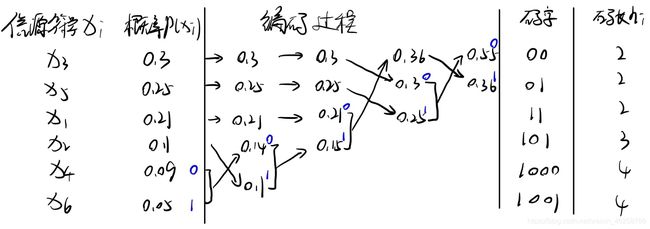我选择的顺序是每次进行码元分配是，上面是0下面是1，当然也可以反过来（得到另一种正确的编码结果）。从x4和x6开始，一点一点向上分配码元。直到分配完成后，按照箭头方向进行回溯，即可得到哈夫曼编码。

三、代码及运行结果

3.1根据原理自编程序

那接下来，终于到了开心的写代码环节了。
在编码过程中，比较麻烦的一点在于程序要最后根据箭头方向回溯，所以每一次进行码元分配都要进行映射，所以关键在于映射矩阵reflect的设置（我自己取了这个名字）。

%% 实验四：哈夫曼编码仿真实现
clear all
clc
% 用户输入符号概率
p = input('请输入离散信源概率分布，例如[0.5,0.5]：\n');
N = length(p);

% 将概率排序并获得单步码字排序
code = strings(N-1,N);% 初始化单步过程的码字
reflect = zeros(N-1,N);% 初始化位置对应向量
p_SD = p;% p_SD为每次得到的概率排序数组
for i=1:N-1           % i表示排序后第几个符号
    M = length(p_SD);
    [p_SD,reflect(i,1:M)] = sort(p_SD,'descend');% 将概率从大到小进行排序
    code(i,M) = '1';% 概率最小的是1
    code(i,M-1) = '0';% 概率第二小的暂且定义为0
    p_SD(M-1) = p_SD(M-1)+p_SD(M);% 将最后两个概率相加
    p_SD(M)=[];
end

% 根据位置对应向量和单步过程的码字计算对应码字
CODE = strings(1,N); % 初始化对应码字
for i=1:N
    column = i;
    for m=1:N-1
        [row,column] = find(reflect(m,:)==column);
        CODE(1,i) = strcat(CODE(1,i),code(m,column));
        % 将最小的两个概率映射成一个
        if column==N+1-m
            column = column-1;
        end
    end
end
CODE = reverse(CODE);

% 计算平均码长
for i=1:N
    L(i) = size(char(CODE(1,i)),2);
end
L_ave = sum(L.*p);      
H = sum(-p.*log2(p));   % 计算信源信息熵
yita = H/L_ave;         % 计算编码效率

% 展示输出码字、平均码长和编码效率
disp(['信号符号  ',num2str(1:N)]);
disp(['对应概率  ',num2str(p)]);
disp(['对应码字  ',CODE]);
disp(['平均码长',num2str(L_ave)]);
disp(['编码效率',num2str(yita)]);

输出上面的实例作为参数，运行结果如下：
当然也可以调用映射矩阵reflect出来看一下：

3.2利用MATLAB内嵌函数

没错，虽然上面搞了这么多，但其实MATLAB有哈夫曼编码的内嵌函数。它就是 huffmandict。
huffmandict函数：
输入：

1. 符号symbols
2. 各符号对应概率p

输出：

1. 哈夫曼编码码字及对应符号dict（一个两行的元胞矩阵）
2. 平均码长L_ave

%% 实验四：哈夫曼编码仿真实现-使用内嵌函数
clear all
clc
% 用户输入符号概率
p = input('请输入离散信源概率分布，例如[0.5,0.5]：\n');
N = length(p);

symbols = cell(1,N);
for i=1:N         % i表示第几个符号
    symbols{i} = ['x',num2str(i)];
end
[dict,L_ave] = huffmandict(symbols,p);
dict = dict.';
H = sum(-p.*log2(p));% 计算信源信息熵
yita = H/L_ave;      % 计算编码效率

CODE = strings(1,N); % 初始化对应码字
for i=1:N            % i表示第几个符号
    CODE(i) = num2str(dict{2,i});
end

% 展示输出码字、平均码长和编码效率
fprintf('\n运行结果:\n');
disp('信源符号：');disp(dict(1,1:N));
disp(['对应概率：',num2str(p)]);
disp('对应码字：');disp(CODE);
disp(['平均码长：',num2str(L_ave)]);
disp(['编码效率：',num2str(yita)]);

输出结果：

四、程序自评价

还是关于控制台输出结果的问题，由于我太懒了，所以这个实验三遗留的问题就这样吧。反正已经 get 到 Huffman 了，嘿嘿~

另外，从鲁棒性考虑，我没用写当出现用户输入概率和不为1等异常情况解决的代码，所以本程序很脆弱，如果大家用到我的程序可以考虑改进一下~

代码原创，但因为原理编写参考到了实验课的指导书，假如有什么不对的地方，侵删。