PTA 浙大第四版 C语言练习
PTA 浙大版《C语言程序设计实验与习题指导(第4版)》
- 开始前说的话
PTA是一个很注重格式输出的练习题库
所以严格禁止提交的答案中,有像自己的提示输入一样的额外内容
例如 printf("请输入x:");
严格禁止汉字存在,注释也不行
本文代码全部是按照我的理解编写
测试使用平台为DEV C++,文中代码全部经过测试后才上传
刚刚开始更新 争取11月底前更新完成
代码如有雷同纯属巧合,仅供学习参考
函数题目录
- PTA 浙大版《C语言程序设计实验与习题指导(第4版)》
-
- 实验2-5-1
-
- 解答
- 实验2-5-5 简单实现x的n次方
-
- 解答
- 实验4-2-2 使用函数求e的近似值
-
- 解答
- 实验5-1 使用函数计算两点间的距离
-
- 解答
- 实验5-2 符号函数
-
- 解答
- 实验5-3 使用函数求Fibonacci数
-
- 解答
- 实验5-4 输出每个月的天数
-
- 解答
- 实验5-5 使用函数求最大公约数
-
- 解答
- 实验5-6 使用函数求素数和
-
- 解答
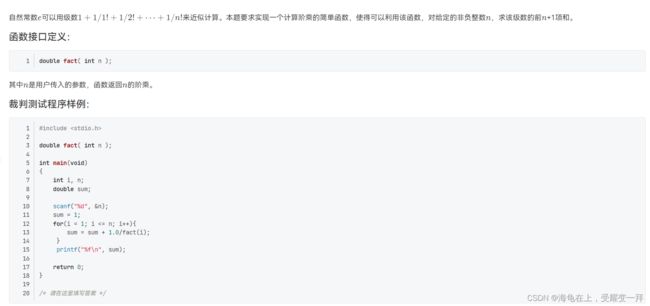
实验2-5-1
#include 解答
思路:求阶乘
double fact( int n ){
int sum;
sum=1;
while(n) {
sum=sum*n;
n--;
}
return sum;
}
测试了一下,发现sum 只有10位,想到sum是int型,改用flout结果正确
double fact( int n ){
float sum;
sum=1;
while(n) {
sum=sum*n;
n--;
}
return sum;
}
实验2-5-5 简单实现x的n次方
#include 解答
幂次方计算,和上题一样 注意输出变量的类型
double mypow( double x, int n )
{
double sum;
sum=1;
while(n){
sum=sum*x;
n--;
}
return sum;
}
实验4-2-2 使用函数求e的近似值
#include 解答
同第一题
double fact( int n ){
float sum;
sum=1;
while(n) {
sum=sum*n;
n--;
}
return sum;
}
实验5-1 使用函数计算两点间的距离
#include 解答
核心思路:
1 分别求两点坐标横坐标和纵坐标的差值x和y
2 两点之间的距离=根号下x^2 +y^2
double dist( double x1, double y1, double x2, double y2 ){
double sum,x,y;
x=x2-x1;
y=y2-y1;
sum=sqrt(x*x+y*y);
return sum;
}
实验5-2 符号函数
#include 解答
注意if的()里是==,单个=是赋值语句
int sign( int x ){
if(x==0){
return 0;
}
else if(x<0){
return -1;
}
else {
return 1;
}
}
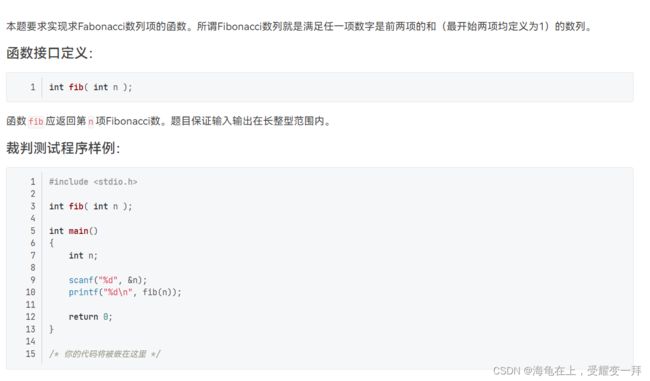
实验5-3 使用函数求Fibonacci数
#include 解答
先解释一下Fabonacci数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列,
因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,
故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……
在数学上,斐波那契数列以如下被以递推的方法定义:
F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)
核心就是
F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)
所以要分类讨论
并且,第n位的数字是经过n-1次相加得到的,即循环n-1次
(可以根据n个数字中间有n-1个空隙想象一下)
int fib( int n ){
int a,b,sum;
a=0;
b=1;
sum=0;
if(n==0){
return 0;
}
else if(n==1){
return 1;
}
else{
while(n-1){
sum=a+b;
a=b;
b=sum;
n--;
}
return sum;
}
}
实验5-4 输出每个月的天数
#include 解答
核心思路:
一、 判断闰年两个条件
1.能被 4 整除但不能被 100 整除
2.能被 400 整除
int MonthDays(int year, int month){
int rm[13]={0,31,29,31,30,31,30,31,31,30,31,30,31};
int pm[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};
if((year%4==0&&year%100!=0)||(year%400==0)){
return rm[month];
}
else{
return pm[month];
}
}
二、取月份
利用数组下标,本题也能这样做
int MonthDays(int year, int month){
int rm[12]={31,29,31,30,31,30,31,31,30,31,30,31};
int pm[12]={31,28,31,30,31,30,31,31,30,31,30,31};
if((year%4==0&&year%100!=0)||(year%400==0)){
return rm[month-1];
}
else{
return pm[month-1];
}
}
实验5-5 使用函数求最大公约数
#include 解答
辗转相除法
辗转相除法
辗转相除法:辗转相除法是求两个自然数的最大公约数的一种方法,也叫欧几里德算法。
例如,求(319,377):
∵ 319÷377=0(余319)
∴(319,377)=(377,319);
∵ 377÷319=1(余58)
∴(377,319)=(319,58);
∵ 319÷58=5(余29)
∴ (319,58)=(58,29);
∵ 58÷29=2(余0)
∴ (58,29)= 29;
∴ (319,377)=29。
核心思路:
保证x>y,左边除右边直到除尽,除尽的那个数就是最大公约数
int gcd( int x, int y ){
int yu;
while(x%y!=0){
if(y>x){
yu=x;
x=y;
y=yu;
}
yu=x-y;
x=y;
y=yu;
}
return y;
}
实验5-6 使用函数求素数和
#include