1.8学习总结

今天依旧是巩固并查集的巩固，但是有附加上其他的知识点。

---

题目描述

明天就是母亲节了，电脑组的小朋友们在忙碌的课业之余挖空心思想着该送什么礼物来表达自己的心意呢？听说在某个网站上有卖云朵的，小朋友们决定一同前往去看看这种神奇的商品，这个店里有 nn 朵云，云朵已经被老板编号为 1,2,3,...,n1,2,3,...,n，并且每朵云都有一个价值，但是商店的老板是个很奇怪的人，他会告诉你一些云朵要搭配起来买才卖，也就是说买一朵云则与这朵云有搭配的云都要买，电脑组的你觉得这礼物实在是太新奇了，但是你的钱是有限的，所以你肯定是想用现有的钱买到尽量多价值的云。

输入格式

第一行输入三个整数，n,m,wn,m,w，表示有 nn 朵云，mm 个搭配和你现有的钱的数目。

第二行至 n+1n+1 行，每行有两个整数， c_i,d_ici​,di​，表示第 ii 朵云的价钱和价值。

第 n+2n+2 至 n+1+mn+1+m 行 ，每行有两个整数 u_i,v_iui​,vi​。表示买第 u_iui​ 朵云就必须买第 v_ivi​ 朵云,同理，如果买第 v_ivi​ 朵就必须买第 u_iui​ 朵。

输出格式

一行，表示可以获得的最大价值。

输入输出样例

输入 #1复制

5 3 10
3 10
3 10
3 10
5 100
10 1
1 3
3 2
4 2

输出 #1复制

1

---

题解：这道题涉及课并查集和基础动态规划的知识点

首先主要并查集，很模板。

其次是动态规划，最简单的滚动数组

幸好这道题是最简单的动态规划，背包问题。

#include 
int n,m,w;
int ans;
int p[10010];//钱
int q[10010];//价值
int dp[1000005];
int a[10010];
int max(int x,int y)
{
    if(x>=y)
        return x;
    else return y;
}
void init()//并查集初始化
{
    for(int i=1; i<=n; i++)
    {
        a[i]=i;
    }
}
int find(int x)//并查集最基本查找
{
    if(a[x]==x)
        return x;
    return find(a[x]);
}
int join(int x,int y)//并查集合集
{
    int fx=find(x);
    int fy=find(y);
    if(fx!=fy)
    {
        a[fx]=fy;
        p[fy]+=p[fx];//累加
        q[fy]+=q[fx];
    }
}
int main()
{
    scanf("%d%d%d",&n,&m,&w);
    init();
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&p[i],&q[i]);
    }
    for(int i=1;i<=m;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        join(x,y);
    }
    for(int i=1;i<=n;i++)
    {
        if(a[i]==i)
        {
            for(int j=w;j>=p[i];j--)
            {
                dp[j]=max(dp[j],dp[j-p[i]]+q[i]);//动态规划
            }
        }
    }
    printf("%d\n",dp[w]);
    return 0;
}

---

题目背景
小明在 A 公司工作，小红在 B 公司工作。

题目描述
这两个公司的员工有一个特点：一个公司的员工都是同性。

A 公司有 NN 名员工，其中有 PP 对朋友关系。B 公司有 MM 名员工，其中有 QQ 对朋友关系。朋友的朋友一定还是朋友。

每对朋友关系用两个整数 (X_i,Y_i)(X 
i
​
 ,Y 
i
​
 ) 组成，表示朋友的编号分别为 X_i,Y_iX 
i
​
 ,Y 
i
​
 。男人的编号是正数，女人的编号是负数。小明的编号是 11，小红的编号是 -1−1。

大家都知道，小明和小红是朋友，那么，请你写一个程序求出两公司之间，通过小明和小红认识的人最多一共能配成多少对情侣（包括他们自己）。

输入格式
输入的第一行，包含 44 个空格隔开的正整数 N,M,P,QN,M,P,Q。

之后 PP 行，每行两个正整数 X_i,Y_iX 
i
​
 ,Y 
i
​
 。

之后 QQ 行，每行两个负整数 X_i,Y_iX 
i
​
 ,Y 
i
​
 。

输出格式
输出一行一个正整数，表示通过小明和小红认识的人最多一共能配成多少对情侣（包括他们自己）。

输入输出样例
输入 #1复制
4 3 4 2
1 1
1 2
2 3
1 3
-1 -2
-3 -3
输出 #1复制
2

---

题解：考查知识点：并查集

开始看到这题的时候有一点迷茫，毕竟要如何用并查集确定情侣呢？很迷茫很迷茫，不知道如何写，后来发现其实很简单，因为一对情侣需要一个男生和一个女生，那么只要分别找出和小明小红有关的男生女生的个数，看那个小就输出哪个就好了。

还有一点就是写的时候函数有点多，开始写的时候完全没发现女生合并函数里的寻找函数写错了，结果答案完全不对，然后回去看才发现。

#include
int n,m,p,q;
int boy,girl;
int a[100005];//男生
int b[100005];//女生
void init()//初始化
{
    for(int i=1; i<=n; i++)
    {
        a[i]=i;
    }
    for(int i=1; i<=m; i++)
    {
        b[i]=i;
    }
}
int find_b(int x)//男生查找
{
    if(a[x]==x)
        return x;
    else return find_b(a[x]);
}
int find_g(int x)//女生查找
{
    if(b[x]==x)
        return x;
    else return find_g(b[x]);
}
int join_b(int x,int y)//男生合并
{
    int fx=find_b(x);
    int fy=find_b(y);
    if(fx!=fy)
    {
        a[fx]=fy;
    }
}
int join_g(int x,int y)//女生合并
{
    int fx=find_g(x);
    int fy=find_g(y);
    if(fx!=fy)
    {
        b[fx]=fy;
    }
}
int main()
{
    scanf("%d%d%d%d",&n,&m,&p,&q);
    int h,j,k,l;
    init();
    for(int i=1; i<=p; i++)
    {
        scanf("%d%d",&h,&j);
        join_b(h,j);
    }
    for(int i=1; i<=q; i++)
    {
        scanf("%d%d",&k,&l);
        k=-k;//将负数变为正数
        l=-l;
        join_g(k,l);
    }
    boy=girl=0;
    for(int i=1; i<=n; i++)
    {
        if(find_b(a[i])==find_b(a[1]))//如果和小明有关系则男生人数增加
            boy++;
    }
    for(int i=1; i<=m; i++)
    {
        if(find_g(b[i])==find_g(b[1]))//如果和小红有关系则女生人数增加
            girl++;
    }
    int min;
    if(boy>girl)
        min=girl;
    else if(boy

---

Takahashi is a cashier.

There is a cash register with 1111 keys: 00, 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The cash register initially displays 00. Whenever he types the key 00, the displayed number is multiplied by 100100; whenever he types one of the others, the displayed number is multiplied by 1010, and then added by the number written on the key.

Takahashi wants the cash register to display an integer SS. At least how many keystrokes are required to make it display SS?

Constraints

• 1\leq S\leq 10^{100000}1≤S≤10100000
• SS is an integer.

Input

The input is given from Standard Input in the following format:

SS

Output

Print the answer in a line.

Sample 1

Inputcopy	Outputcopy
40004	4

For example, the following four keystrokes make the cash register display 4000440004. Initially, the cash register displays 00.

• Type the key 4. It now displays 44.
• Type the key 00. It now displays 400400.
• Type the key 0. It now displays 40004000.
• Type the key 4. It now displays 4000440004.

He cannot make it display 4000440004 with three or fewer keystrokes, so 44 should be printed.

Sample 2

Inputcopy	Outputcopy
1355506027	10

Sample 3

Inputcopy	Outputcopy
10888869450418352160768000001	27

Note that SS may not fit into a 6464-\operatorname{bit}bit integer type.

---

题目大意就是给你一串数字和十一个按键，你要按多少次。

题解：找最特殊的那个：00，其他的按键都是每个按一次就计数器增加一次，只有00需要数组下标a[i]&&a[i+1]同时为字符零计数器加一，下标也要加一。

#include 
#include 
char a[10000005]={0};
unsigned long long int cnt=0;
int main()
{
    scanf("%s",a);
    unsigned long long int leng=strlen(a);
    for(int i=0;i

---

You are given a simple undirected graph with NN vertices numbered 11 to NN and MM edges numbered 11 to MM. Edge ii connects vertex u_iui​ and vertex v_ivi​.
Find the number of connected components in this graph.

Notes

A simple undirected graph is a graph that is simple and has undirected edges.
A graph is simple if and only if it has no self-loop or multi-edge.

A subgraph of a graph is a graph formed from some of the vertices and edges of that graph.
A graph is connected if and only if one can travel between every pair of vertices via edges.
A connected component is a connected subgraph that is not part of any larger connected subgraph.

Constraints

• 1 \leq N \leq 1001≤N≤100
• 0 \leq M \leq \frac{N(N - 1)}{2}0≤M≤2N(N−1)​
• 1 \leq u_i, v_i \leq N1≤ui​,vi​≤N
• The given graph is simple.
• All values in the input are integers.

Input

The input is given from Standard Input in the following format:

NN MM
u_1u1​ v_1v1​
u_2u2​ v_2v2​
\vdots⋮
u_MuM​ v_MvM​

Output

Print the answer.

Sample 1

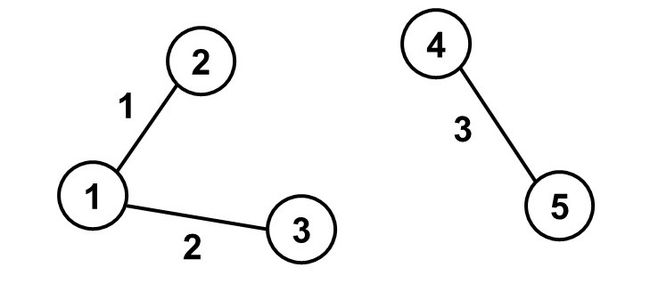
Inputcopy	Outputcopy
5 3 1 2 1 3 4 5	2

The given graph contains the following two connected components:

• a subgraph formed from vertices 11, 22, 33, and edges 11, 22;
• a subgraph formed from vertices 44, 55, and edge 33.

Sample 2

Inputcopy	Outputcopy
5 0	5

Sample 3

Inputcopy	Outputcopy
4 6 1 2 1 3 1 4 2 3 2 4 3 4	1

---

题意：给你一个数字n，然后给你m对关系u,v，让你发现能最后能合并成多少个图。（相当于你能合成多少个宗门）

其实就是并查集的考察 ，将同属于一个门派的合并

#include 
int n,m;
int a[10010];
struct node
{
    int x;
    int y;
} k[100010],temp;
void init()//初始化
{
    for(int i=1; i<=n; i++)
    {
        a[i]=i;
    }
}
int find(int x)//查找
{
    if(a[x]==x)
        return x;
    return find(a[x]);
}
int join(int x,int y)//合并
{
    int fx=find(x);
    int fy=find(y);
    if(fx!=fy)
    {
        a[fx]=fy;
        return 1;
    }
    else return 0;
}
int main()
{
    scanf("%d%d",&n,&m);
    int cnt=n;
        init();
    for(int i=1; i<=m; i++)
    {
        scanf("%d%d",&k[i].x,&k[i].y);
        if(join(k[i].x,k[i].y))//当合并成功
        {
            cnt--;
        }
    }
    printf("%d\n",cnt);
    return 0;
}