C#,码海拾贝(09)——阿克玛(Akima)曲线光滑插值算法,《C#数值计算算法编程》源代码升级改进版
Akima插值既有一维插值(曲线插值),也有二维插值(曲面插值)
对于一维插值,参考以下网页:
[校园网]
对于二维插值,参考以下网页:
【校园网】
Akima样条插值法是用双五次多项式和连续的一阶偏导数进行光滑曲面拟合和内插的方法,该方法将平面分割为三角形格网,各三角形以三个数据点在平面上的投影点为顶点。
根据三个顶点的场值、一阶偏导数和二阶偏导数值,可得到18个不相关的条件,三角形三条边两侧的一阶偏导数相等给出另外三个边界条件,这样可求出方程的21个系数。
Akima插值法在各子区间内采用三次多项式函数逼近,利用一个点加上该点前后各两点共5个数据点来计算中间点的导数值,是一种一阶光滑性的局域插值方法。
The Akima interpolation is a continuously differentiable sub-spline interpolation. It is built from piecewise third order polynomials. Only data from the next neighbor points is used to determine the coefficients of the interpolation polynomial. There is no need to solve large equation systems and therefore this interpolation method is computationally very efficient. Because no functional form for the whole curve is assumed and only a small number of points is taken into account this method does not lead to unnatural wiggles in the resulting curve. The monotonicity of the specified data points is not necessarily retained by the resulting interpolation function. By additional constraints on the estimated derivatives a monotonicity preserving interpolation function can be constructed .
Akima插值是一种连续可微的子样条插值。它是由分段三阶多项式建立的。仅使用来自下一个相邻点的数据来确定插值多项式的系数。不需要求解大型方程组,因此这种插值方法在计算上非常有效。因为没有假设整个曲线的函数形式,并且只考虑了少量的点,所以这种方法不会导致结果曲线中出现不自然的摆动。指定数据点的单调性不一定会被得到的插值函数所保留。通过对估计导数的附加约束,可以构造保持单调性的插值函数。
using System;
using System.Drawing;
using System.Collections;
using System.Collections.Generic;
namespace Zhou.CSharp.Algorithm
{
///
/// 插值计算类Interpolation.cs
/// 作者:周长发
/// 改编:深度混淆
/// https://blog.csdn.net/beijinghorn
///
public static partial class Interpolation
{
///
/// 光滑不等距插值
///
/// 一维数组,长度为n,存放给定的n个结点的值x(i),要求x(0)
/// 一维数组,长度为n,存放给定的n个结点的函数值y(i),y(i) = f(x(i)), i=0,1,...,n-1
/// 存放指定的插值点的x值
/// 控制参数,若k>=0,则只计算第k个子区间[x(k), x(k+1)]上的三次多项式的系数
/// 一维数组,长度为5,其中s(0),s(1),s(2),s(3)返回三次多项式的系数,s(4)返回指定插值点t处的函数近似值f(t)(k<0时)或任意值(k>=0时)
/// 指定的查指点t的函数近似值f(t)
public static double Akima(double[] x, double[] y, double t, int k, out double[] s)
{
int n = x.Length;
s = new double[5] { 0.0, 0.0, 0.0, 0.0, 0.0 };
// 特例处理
if (n < 1)
{
return s[4];
}
else if (n == 1)
{
s[0] = y[0];
s[4] = y[0];
return s[4];
}
else if (n == 2)
{
s[0] = y[0];
s[1] = (y[1] - y[0]) / (x[1] - x[0]);
if (k < 0)
{
s[4] = (y[0] * (t - x[1]) - y[1] * (t - x[0])) / (x[0] - x[1]);
}
return s[4];
}
// 插值
int kk = 0;
if (k < 0)
{
if (t <= x[1])
{
kk = 0;
}
else if (t >= x[n - 1])
{
kk = n - 2;
}
else
{
kk = 1;
int m = n;
while (((kk - m) != 1) && ((kk - m) != -1))
{
int w = (kk + m) / 2;
if (t < x[w - 1])
{
m = w;
}
else
{
kk = w;
}
}
kk = kk - 1;
}
}
else
{
kk = k;
}
double[] u = new double[5];
if (kk >= n - 1)
{
kk = n - 2;
}
u[2] = (y[kk + 1] - y[kk]) / (x[kk + 1] - x[kk]);
if (n == 3)
{
if (kk == 0)
{
u[3] = (y[2] - y[1]) / (x[2] - x[1]);
u[4] = 2.0 * u[3] - u[2];
u[1] = 2.0 * u[2] - u[3];
u[0] = 2.0 * u[1] - u[2];
}
else
{
u[1] = (y[1] - y[0]) / (x[1] - x[0]);
u[0] = 2.0 * u[1] - u[2];
u[3] = 2.0 * u[2] - u[1];
u[4] = 2.0 * u[3] - u[2];
}
}
else
{
if (kk <= 1)
{
u[3] = (y[kk + 2] - y[kk + 1]) / (x[kk + 2] - x[kk + 1]);
if (kk == 1)
{
u[1] = (y[1] - y[0]) / (x[1] - x[0]);
u[0] = 2.0 * u[1] - u[2];
if (n == 4)
{
u[4] = 2.0 * u[3] - u[2];
}
else
{
u[4] = (y[4] - y[3]) / (x[4] - x[3]);
}
}
else
{
u[1] = 2.0 * u[2] - u[3];
u[0] = 2.0 * u[1] - u[2];
u[4] = (y[3] - y[2]) / (x[3] - x[2]);
}
}
else if (kk >= (n - 3))
{
u[1] = (y[kk] - y[kk - 1]) / (x[kk] - x[kk - 1]);
if (kk == (n - 3))
{
u[3] = (y[n - 1] - y[n - 2]) / (x[n - 1] - x[n - 2]);
u[4] = 2.0 * u[3] - u[2];
if (n == 4)
{
u[0] = 2.0 * u[1] - u[2];
}
else
{
u[0] = (y[kk - 1] - y[kk - 2]) / (x[kk - 1] - x[kk - 2]);
}
}
else
{
u[3] = 2.0 * u[2] - u[1];
u[4] = 2.0 * u[3] - u[2];
u[0] = (y[kk - 1] - y[kk - 2]) / (x[kk - 1] - x[kk - 2]);
}
}
else
{
u[1] = (y[kk] - y[kk - 1]) / (x[kk] - x[kk - 1]);
u[0] = (y[kk - 1] - y[kk - 2]) / (x[kk - 1] - x[kk - 2]);
u[3] = (y[kk + 2] - y[kk + 1]) / (x[kk + 2] - x[kk + 1]);
u[4] = (y[kk + 3] - y[kk + 2]) / (x[kk + 3] - x[kk + 2]);
}
}
s[0] = Math.Abs(u[3] - u[2]);
s[1] = Math.Abs(u[0] - u[1]);
double p = 0.0;
double q = 0.0;
if ((s[0] + 1.0 == 1.0) && (s[1] + 1.0 == 1.0))
{
p = (u[1] + u[2]) / 2.0;
}
else
{
p = (s[0] * u[1] + s[1] * u[2]) / (s[0] + s[1]);
}
s[0] = Math.Abs(u[3] - u[4]);
s[1] = Math.Abs(u[2] - u[1]);
if ((s[0] + 1.0 == 1.0) && (s[1] + 1.0 == 1.0))
{
q = (u[2] + u[3]) / 2.0;
}
else
{
q = (s[0] * u[2] + s[1] * u[3]) / (s[0] + s[1]);
}
s[0] = y[kk];
s[1] = p;
s[3] = x[kk + 1] - x[kk];
s[2] = (3.0 * u[2] - 2.0 * p - q) / s[3];
s[3] = (q + p - 2.0 * u[2]) / (s[3] * s[3]);
if (k < 0)
{
p = t - x[kk];
s[4] = s[0] + s[1] * p + s[2] * p * p + s[3] * p * p * p;
}
return s[4];
}
///
/// 光滑等距插值
///
/// 等距n个结点中第一个结点的值
/// 等距结点的步长
/// 一维数组,长度为n,存放给定的n个结点的函数值y(i),y(i) = f(x(i)), i=0,1,...,n-1
/// 存放指定的插值点的x值
/// 控制参数,若k>=0,则只计算第k个子区间[x(k), x(k+1)]上的三次多项式的系数
/// 一维数组,长度为5,其中s(0),s(1),s(2),s(3)返回三次多项式的系数,s(4)返回指定插值点t处的函数近似值f(t)(k<0时)或任意值(k>=0时)
/// 指定的查指点t的函数近似值f(t)
public static double Akima(double x0, double step, double[] y, double t, out double[] s, int k)
{
int n = y.Length;
s = new double[5] { 0.0, 0.0, 0.0, 0.0, 0.0 };
// 特例处理
if (n < 1)
{
return s[4];
}
else if (n == 1)
{
s[0] = y[0];
s[4] = y[0];
return s[4];
}
else if (n == 2)
{
s[0] = y[0];
s[1] = (y[1] - y[0]) / step;
if (k < 0)
{
s[4] = (y[1] * (t - x0) - y[0] * (t - x0 - step)) / step;
}
return s[4];
}
// 插值
int kk = 0;
if (k < 0)
{
if (t <= x0 + step)
{
kk = 0;
}
else if (t >= x0 + (n - 1) * step)
{
kk = n - 2;
}
else
{
kk = 1;
int m = n;
while (((kk - m) != 1) && ((kk - m) != -1))
{
int w = (kk + m) / 2;
if (t < x0 + (w - 1) * step)
{
m = w;
}
else
{
kk = w;
}
}
kk = kk - 1;
}
}
else
{
kk = k;
}
if (kk >= n - 1)
{
kk = n - 2;
}
double[] u = new double[5];
u[2] = (y[kk + 1] - y[kk]) / step;
if (n == 3)
{
if (kk == 0)
{
u[3] = (y[2] - y[1]) / step;
u[4] = 2.0 * u[3] - u[2];
u[1] = 2.0 * u[2] - u[3];
u[0] = 2.0 * u[1] - u[2];
}
else
{
u[1] = (y[1] - y[0]) / step;
u[0] = 2.0 * u[1] - u[2];
u[3] = 2.0 * u[2] - u[1];
u[4] = 2.0 * u[3] - u[2];
}
}
else
{
if (kk <= 1)
{
u[3] = (y[kk + 2] - y[kk + 1]) / step;
if (kk == 1)
{
u[1] = (y[1] - y[0]) / step;
u[0] = 2.0 * u[1] - u[2];
if (n == 4)
{
u[4] = 2.0 * u[3] - u[2];
}
else
{
u[4] = (y[4] - y[3]) / step;
}
}
else
{
u[1] = 2.0 * u[2] - u[3];
u[0] = 2.0 * u[1] - u[2];
u[4] = (y[3] - y[2]) / step;
}
}
else if (kk >= (n - 3))
{
u[1] = (y[kk] - y[kk - 1]) / step;
if (kk == (n - 3))
{
u[3] = (y[n - 1] - y[n - 2]) / step;
u[4] = 2.0 * u[3] - u[2];
if (n == 4)
{
u[0] = 2.0 * u[1] - u[2];
}
else
{
u[0] = (y[kk - 1] - y[kk - 2]) / step;
}
}
else
{
u[3] = 2.0 * u[2] - u[1];
u[4] = 2.0 * u[3] - u[2];
u[0] = (y[kk - 1] - y[kk - 2]) / step;
}
}
else
{
u[1] = (y[kk] - y[kk - 1]) / step;
u[0] = (y[kk - 1] - y[kk - 2]) / step;
u[3] = (y[kk + 2] - y[kk + 1]) / step;
u[4] = (y[kk + 3] - y[kk + 2]) / step;
}
}
s[0] = Math.Abs(u[3] - u[2]);
s[1] = Math.Abs(u[0] - u[1]);
double p = 0.0;
if ((s[0] + 1.0 == 1.0) && (s[1] + 1.0 == 1.0))
{
p = (u[1] + u[2]) / 2.0;
}
else
{
p = (s[0] * u[1] + s[1] * u[2]) / (s[0] + s[1]);
}
s[0] = Math.Abs(u[3] - u[4]);
s[1] = Math.Abs(u[2] - u[1]);
double q = 0.0;
if ((s[0] + 1.0 == 1.0) && (s[1] + 1.0 == 1.0))
{
q = (u[2] + u[3]) / 2.0;
}
else
{
q = (s[0] * u[2] + s[1] * u[3]) / (s[0] + s[1]);
}
s[0] = y[kk];
s[1] = p;
s[3] = step;
s[2] = (3.0 * u[2] - 2.0 * p - q) / s[3];
s[3] = (q + p - 2.0 * u[2]) / (s[3] * s[3]);
if (k < 0)
{
p = t - (x0 + kk * step);
s[4] = s[0] + s[1] * p + s[2] * p * p + s[3] * p * p * p;
}
return s[4];
}
}
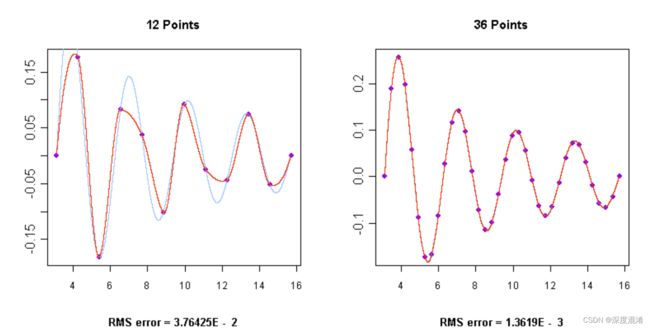
} Akima 插值法和三次样条函数一样考虑了要素导数值的效应,因而得到的整个插值曲线是光滑的。三次样条函数插值法具有最小模、最佳最优逼近和收敛的特性,而 Aikma 插值法所得曲线比样条函数插值曲线更光顺,更自然。
POWER BY 315SOFT.COM
Akima样条插值法是用双五次多项式和连续的一阶偏导数进行光滑曲面拟合和内插的方法,该方法将平面分割为三角形格网,各三角形以三个数据点在平面上的投影点为顶点。
基于坐标点的计算,从点集计算插值曲线等拓展方法请参阅《拉格朗日插值算法及其拓展》