置信椭圆（误差椭圆）详解

Part.I 预备知识

Chap.I 一些概念

首先要了解一下下面的概念：

• 点估计：设总体X的分布函数的形式已知，但它的一个或多个参数未知，借助于总体X的一个样本来估计总体未知参数的值的问题称为参数的点估计问题。
• 对于一个未知量，人们在测量或计算时，常不以得到近似值为满足，还需估计误差，即要求知道近似值的精确程度(亦即所求真值所在的范围)。类似地，对于未知参数 $\theta$，除了求出它的点估计 $\hat{\theta }$ 外，我们还希望估计出一个范围，并希望知道这个范围包含参数 $\theta$ 真值的可信程度。这样的范围通常以区间的形式给出，同时还给出此区间包含参数 $\theta$ 真值的可信程度。这种形式的估计称为区间估计，这样的区间即所谓置信区间。
• 置信区间：Confidence interval 设总体 X 的分布函数 $F(x;\theta )$ 含有一个未知参数 $\theta$，$\theta \in \Theta$ （$\Theta$ 是 $\theta$ 可能取值的范围），对于给定值 $\alpha$（$0<\alpha <1$），若由来自 X 的样本 $X_1,X_2,\cdots ,X_n$ 确定的两个统计量 $\underline{\theta }=\underline{\theta }(X_1,X_2,\cdots ,X_n)$ 和 $\overline{\theta }=\overline{\theta }(X_1,X_2,\cdots ,X_n)(\underline{\theta }<\overline{\theta })$ ，对于任意 $\theta <\Theta$ 满足 $P\{\underline{\theta }(X_1,X_2,\cdots ,X_n)<\theta <\overline{\theta }(X_1,X_2,\cdots ,X_n)\}\ge 1-\alpha$，则称随机区间 $(\underline{\theta },\overline{\theta })$ 是 $\theta$ 的置信水平为 $1-\alpha$ 的置信区间，$\underline{\theta }$ 和 $\overline{\theta }$ 分别称为置信水平为 $1-\alpha$ 的双侧置信区间的置信下限和置信上限，$1-\alpha$ 称为置信水平。
• 上面给出了置信区间严格的数学定义，通俗的讲，置信区间展现的是这个参数的真实值有一定的带来落在测量结果的程度，其给出的是被量测参数的量测值的可信程度（置信水平），一般常用 $95\%$ 置信水平。
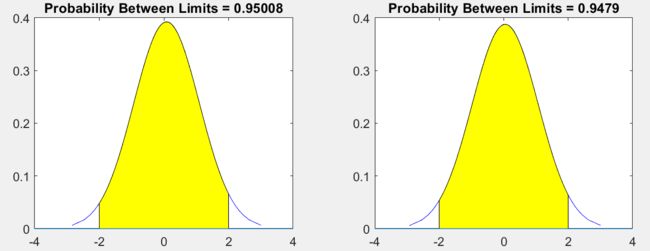
• $68-95-99.7$ 法则：或者叫做 $3\sigma$ 原则。对于正态分布，$68\%$ 的数据分布在距离均值1个方差的范围；$95\%$ 的数据分布在距离均值2个方差的范围；$99.7\%$ 的数据分布在距离均值3个方差的范围内。

Chap.II 主成分分析

主成分分析 (Principal Component Analysis, PCA) 是一种统计方法，通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。PCA 的主要应用有：降维、特征提取、去噪、故障检测。

• PCA 的主要思想是将 $n$ 维特征映射到 $k$ 维上，这 $k$ 维是全新的正交特征也被称为主成分，是在原有 $n$ 维特征的基础上重新构造出来的 $k$ 维特征。
• PCA 的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推，可以得到 $n$ 个这样的坐标轴。通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面 $k$ 个坐标轴中，后面的坐标轴所含的方差几乎为0。于是，我们可以忽略余下的坐标轴，只保留前面 $k$ 个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

Chap.III Matlab 函数 randn

下面的实例中会用到 Matlab 中生成正态分布随机数的函数randn()，下面对其用法做简要的介绍。

• randn：产生均值为0、方差为1的高斯白噪声，常用的用法有下面几种
• randn(n)：产生一个 n*n 的随机数方阵
• randn(m,n)：产生一个 m*n 的随机数矩阵

---

除此之外还有，Matlab 关于随机数的生成函数还有：

• rand：产生均值为0.5、幅度在0~1之间的伪随机数。
• randperm(n)：产生1到n的均匀分布随机序列。
• normrnd(a,b,c,d)：产生均值为a、方差为b大小为c*d服从正态分布的随机矩阵。

---

下面对randn做一个简单的验证：产生两列数据，分别画出它们的概率分布，看看图形是否符合正态分布。代码和绘制结果如下，可以看出结果符合预期。

%% 检验 randn 函数
function rTest()
data=randn(600,2);
figure
hold on
subplot(121)
t=2;
p=capaplot(data(:,1),[-t,t]);
subplot(122)
p=capaplot(data(:,2),[-t,t]);
end

Chap.IV Matlab 函数 pca

function [coeff, score, latent, tsquared, explained, mu] = pca(x,varargin)

输入：x 是样本，N*P=N个样本量，P维

---

输出：

• COEFF，返回N×P数据矩阵X的主成分系数。X的行对应于观测值，列对应于变量。每列系数包含一个主成分的系数。各列按主成分方差（latent）降序排列。默认情况下，PCA将数据居中并使用奇异值分解算法。对于非默认选项，请使用名称/值对参数。
• SCORE，返回主成分得分，它是X在主成分空间中的表示。score的行对应观察值，列对应主成分。中心数据可以用SCORE*COEFF重建。
• LATENT，返回每个主成分方差，即X的协方差矩阵的特征值，特征值从大到小进行排序。
• TSQUARED，返回X中每个观测值的Hotelling T平方统计值。PCA使用所有主分量计算TSQUARED（在整个空间中计算），即使请求的组件较少（请参见下面的“NumComponents”选项）。对于缩小空间中的TSQUARED，使用MAHAL（SCORE，SCORE）。
• EXPLAINED，返回一个向量，其中包含每个主成分方差占总方差的百分比。
• MU，Centered设置为true时返回估计的平均值MU；设置为false时返回所有零。

Part.II 置信椭圆的含义

对于一维的情况，我们可以用置信区间来描述一个值落在某个区间（区域）的概率（置信水平），这个区间用几何表示是一个线段；对于二维的情况，几何意义上就从一条直线变成了一个平面，类似于置信区间，便有了置信椭圆（confidence ellipse）的概念。

---

下面是笔者的思考，一些自说自话罢了。

• 置信椭圆的概念是从置信区间类比而来的，严格意义上讲它描述的仅仅是二维的情况，对于三维可以称之为置信椭球，对于更高维可以称之为置信超椭球（自己瞎起的~）；但是很多情况下，对于二维或者更高维，很多学者也将其称为置信椭圆。
• 为什么叫『椭圆』，不叫『圆』『长方形』呢？因为点的分布从图形上看，可以用一个椭圆将其包裹起来，所以叫椭圆。
• 『误差椭圆』这个概念又是怎么来的？对于二维情况，我们进行多次量测的目的是为了确定一个二维参数的取值，但是我们又不能 $100\%$ 确定我们给出的值就是这个二维参数的真值，但是我们一般可以说这个二维参数有多少概率会落在某个范围内。在给定概率的情况下，这个范围越小，说明我们对我们的量测越有信心，我们量测的精度越高，误差越小。这个范围可以说是我们给出参数的精度或误差，所以便有了『误差椭圆』这个概念，这么说『精度椭圆』这个名词是不是也顺利成章了？

---

Chap.I 一个 Matlab 实例

其实，写这篇博文的初衷是为了搞清楚『为什么两个随机变量不相关，其误差椭圆的长短轴平行于坐标轴』。还是看个例子，用数据说话吧。在看下面的内容之前首先要明确下面几点：

• 我们通过 randn 函数来生成了两列均值为 0 方差为 1 的随机数；我们对这列随机数的理解为：每一列数据都表示对一个『待求量』的多次量测，显然我们已经假设我们的量测存在一个服从高斯分布的噪声，并且我们的『待求量』真值是0。我们也可以将每一列数据理解为对一个『随机变量』的多次抽样或观测。
• randn 函数虽然一次生成了两列数据，但是这两列数据是毫无关联的（当然也可以一次生成一列数据，分两次生成）；换言之，这两列数据代表的两个『随机变量』是不相关的。

Sec.I 两个不相关变量的特征

首先用randn生成了两列均值为0、方差为1的随机数据，数据量是300*n；为了探究不同数据量的区别，因此画了6幅图如下，数据量分别是300*n，n=1,2,3,4,5,6。图中，len表示数据量的大小，a,b 分别表示椭圆长轴和短轴长度；红色和蓝色箭头（好吧，红色可能看不到箭头）分别表示长轴和短轴方向。可以看到，画出来的图形几近于圆，数据量越多，它越接近于圆。但是它的轴并不平行于坐标轴，可以这样解释：因为这两列数据的方差都是1，所以长短轴理论上应该相等，所以画出来的图形理论上应该是个圆（实际情况也是，数据量越多，它越接近于圆），所以其指向就无所谓了。

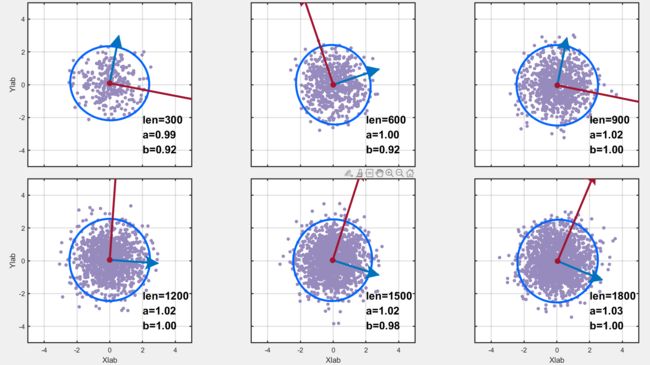
为了让两列数据的方差不同，我们将第一列数据乘上了2，不同数据量的绘图结果如下。可以看到，它确实是长短轴平行于坐标轴的椭圆！！

涉及的绘图代码如下：

%% 两个不相关变量的特性
function Test1(wid,hei,a,b)
figure
pmag=50;  %the size of margin pix
marx(1:b+1,1)=3;marx(1)=8; 
mary(1:a+1,1)=3;mary(1)=8;
sumx=sum(marx);sumy=sum(mary);
marx=marx./sumx;mary=mary./sumy;
lefy=pmag/hei/mary(1);
lefx=pmag/wid/marx(1);
marx=marx.*lefx;
mary=mary.*lefy;
wid1=(1-lefx)/b;
hei1=(1-lefy)/a;

xt=-4:2:4;xtl1=sprintfc('%g',xt);xtl2=kcell(size(xtl1));xl=[-5 5];
yt1=-4:2:4;ytl1=sprintfc('%g',yt1);ytl2=kcell(size(ytl1));yl=[-5 5];

set(gcf,'position',[0 0 wid hei])
for i=1:a
    magy=(a-i)*hei1+sum(mary(1:end-i));
    for j=1:b
        magx=(j-1)*wid1+sum(marx(1:j));
        n=(i-1)*b+j;
        subplot(a,b,n);
        set(gca,'position',[magx magy wid1 hei1],'box','on');
        % plot here!
        len=300;
        data=randn(n*len, 2);       % get the data 
        PCA(data);
        set(gca,'XLim',xl,'XTick',xt,'XTicklabel',xtl2);
        set(gca,'YLim',yl,'YTick',yt1,'YTicklabel',ytl2);
        if j==1
            ylabel('Ylab');
            set(gca,'YTick',yt1,'YTicklabel',ytl1);
        end
        if i==a
            xlabel('Xlab');
            set(gca,'XTick',xt,'XTicklabel',xtl1);
        end
    end
end
end

% get a null cell which is a*b dims
function data=kcell(m)
a=m(1);b=m(2);
data=cell(a,b);
for i=1:a
   for j=1:b
       data(i,j)=cellstr(num2str(data{i,j}));
   end
end
end

%% PCA
function PCA(data)
len=size(data,1);
data(:,1)=2*data(:,1);
center = mean(data);
[coeff, ~, latent, ~, ~] = pca(data);

% r1 r2 为自定义的向量大小参数(模)
r1 = 6;
r2 = 3;
% p1 p2 为第一主轴和第二主轴上的点
p1 = r1*coeff(:, 1)'+center;
p2 = r2*coeff(:, 2)'+center;

% 主轴方向与X轴之间的夹角
angle = cart2pol(coeff(1, :), coeff(2, :))*180/pi;
beta = angle(1, 1);
% 置信椭圆坐标（以 95% 为例）
semimajor = sqrt(latent(1, 1)); % 长轴长度（一半）
semiminor = sqrt(latent(2, 1)); % 短轴长度（一半）
alpha = linspace(0, 360, 2000)';
% 卡方分布表
% https://people.richland.edu/james/lecture/m170/tbl-chi.html
% level = 4.605;  % 90%
level = 5.991;  % 95%
% level = 9.210;  % 99%
% 椭圆坐标点
ellipse_X = center(1, 1)+sqrt(level)*(semimajor*cosd(alpha)*cosd(beta)-...
    semiminor*sind(alpha)*sind(beta));
ellipse_Y = center(1, 2)+sqrt(level)*(semimajor*cosd(alpha)*sind(beta)+...
    semiminor*sind(alpha)*cosd(beta));

%% 可视化
% figure
hold on
box on
grid on
% 原始数据
scatter(data(:, 1), data(:, 2), 15, 'LineWidth', 1.2,...
        'MarkerEdgeColor', [151, 138, 189]/255,...
        'MarkerFaceColor', [151, 138, 189]/255);
xlim([-5, 5]); 
ylim([-5, 5]);
set(gca, 'linewidth', 1.5)

% 置信椭圆
plot(ellipse_X, ellipse_Y, 'Color', [0, 102, 255]/255,...
    'LineStyle', '-', 'LineWidth', 3),

% 第一主轴方向
arrow_1 = annotation('arrow', 'Color', [162, 20, 47]/255,...
    'HeadStyle', 'cback2', 'LineWidth', 3, 'HeadWidth', 20, 'HeadLength', 20);
arrow_1.Parent = gca;
arrow_1.X = [center(1, 1), p1(1, 1)];
arrow_1.Y = [center(1, 2), p1(1, 2)];  

% 第二主轴方向
arrow_2 = annotation('arrow', 'Color', [0, 114, 189]/255,...
    'HeadStyle', 'cback2', 'LineWidth', 3, 'HeadWidth', 20, 'HeadLength', 20);
arrow_2.Parent = gca; 
arrow_2.X = [center(1, 1), p2(1, 1)]; 
arrow_2.Y = [center(1, 2), p2(1, 2)];  

% 中心点
plot(center(1, 1), center(1, 2),...
    'Marker', 'o',...
    'MarkerSize', 8,...
    'MarkerEdgeColor', [162, 20, 47]/255,...
    'MarkerFaceColor', [162, 20, 47]/255);

% title('主轴方向和置信椭圆', 'FontSize', 16, 'FontWeight', 'bold')
str=sprintf('len=%d\na=%.2f\nb=%.2f',len,semimajor,semiminor);
text(2, -3, str, 'FontSize', 16, 'FontWeight', 'bold')
axis equal
end

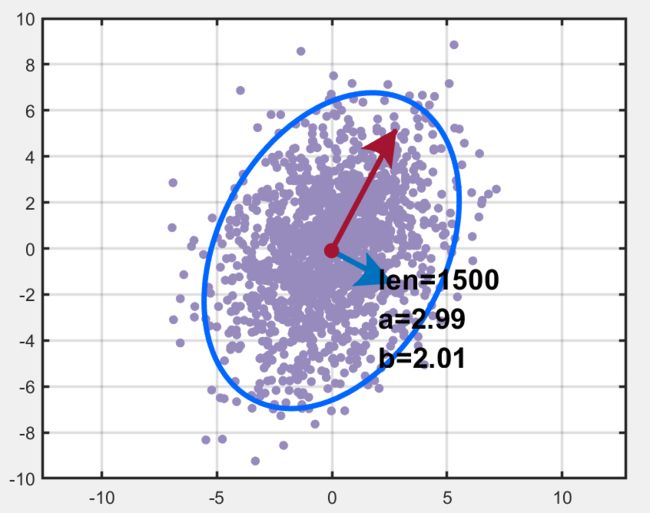
Sec.II 两个相关变量的特征

为了让两个随机变量相关，我们记randn生成的两列数据为 $X=[a,b]$（其中 $a$ 的均值为 0，方差为 2；$b$ 的均值为 0，方差为 1），将其乘上一个矩阵得到新的数据 $Y$：
$$Y=[a^{\prime },b^{\prime }]=[a,b]\cdot \left[\begin{array}{cc}1& 1\\ -1& 2\end{array}\right]=X\cdot Z$$
也就是说，$a^{\prime }=a-b,b^{\prime }=a+2b$，然后我们绘制其置信椭圆如下图所示：

其代码如下：

%% 两个相关变量的特征
function Test2()
len=300;
data=randn(5*len, 2);       % get the data 
data(:,1)=2*data(:,1);      % 第一列方差变为2
data1=zeros(size(data));
Z=[1 1;-1 2];
data1=data*Z;
% data1(:,1)=data(:,1)-data(:,2);
% data1(:,2)=data(:,1)+2*data(:,2);
PCA(data1);
end

---

我们能让两个不相关的随机变量通过乘以一个矩阵变成相关的；同样的我们也可以通过乘一个矩阵使它们『解相关』。对于这组数据，我们已经知道了使它们两个变成相关的矩阵 $Z$，那么再乘 $Z^{-1}$ 显然可以解相关；但是对于一个我们不知道变换矩阵（对应此例也就是上文的 $Z^{-1}$ ） 的数据，我们一般用下面的方法来求『变换阵』。

PS：之前的我还以为用 LU 分解来求变换阵，并且认为求解变换阵的方法是『高斯变换』，变换阵被称为『高斯变换阵』。但是并不是，是通过特征值和特征向量来求的。

Chap.II 变换阵 (解相关矩阵) 的求解

现在的问题是：已知两个随机变量的许多量测（两列数据），而且这两个随机变量是相关的；怎么找到一个矩阵，使得这两列数据乘上这个矩阵之后，这两列数据就不相关了。笔者觉得有两种方法，一种是几何意义上的：将置信椭圆旋转一下，使得其长短轴平行于坐标轴；另一种是纯代数方法：通过矩阵变换找到这样的旋转矩阵（旋转在代数意义上就是乘以一个矩阵）。

实际上，上述问题用主成分分析找主元、降相关就可以解决。

---

基于特征值分解协方差矩阵实现 PCA 算法的步骤

• 输入数据集 $X=\{x_1,x_2,\cdots ,x_n\}$，需要将其降到 $k$ 维
• 去中心化：每一维特征减去各自的均值
• 计算方差-协方差矩阵 $A=\frac{1}{n}{X}^{T}X$ （这里分母是 $n$ 或 $n-1$ 对求出的特征向量没有影响）
• 求出 $A$ 的特征值和特征向量
• 对特征值从大到小排序，选择其中最大的 $k$ 个。然后将其对应的 $k$ 个特征向量分别作为行向量组成特征向量矩阵 $P$
• 将数据转换到 $k$ 个特征向量构建的新空间中，即 $Y=PX$

---

下面对此种方法求『解相关矩阵』进行一个简单的证明。

• 首先要明确，我们的目的是将 $X$ 的协方差矩阵 $A$ 转换为一个对角阵，即 $X^{T}X=A=V^T\Lambda V$，也就是令 $(X{V}^{-1}{)}^T(X{V}^{-1})=\Lambda$，即寻求一个转换阵 $Z=V^{-1}$，使得 $B^{T}B=\Lambda (B=XZ)$
• 关于矩阵分解的方法中，哪种分解方法可以使得矩阵的分解结果中含有一个对角阵呢？奇异值分解 SVD 和特征分解都可以！用这两种分解中的哪种都行！
• 特征分解：$A=V\Lambda V^{-1}$；另外协方差阵是一个实对称阵，对于实对称阵，其不同特征值对应的特征向量正交。又因为特征向量伸缩（乘一个常数）之后还是特征向量，所以我们很容易构造出来一个特征向量矩阵 $V$，使得 $V^T=V^{-1}$.
• 基于上述，有 $X^{T}X=V\Lambda V^{-1}$. 所以我们取转换阵 $Z=V$ 令 $Y=XZ$，$Y^{T}Y=V^T{X}^{T}XV=V^{T}V\Lambda V^{-1}V=V^{-1}V\Lambda V^{-1}V=\Lambda$。这样利用转换阵 $V$ 便将协方差矩阵变成了对角阵，即实现了『解相关』。

---

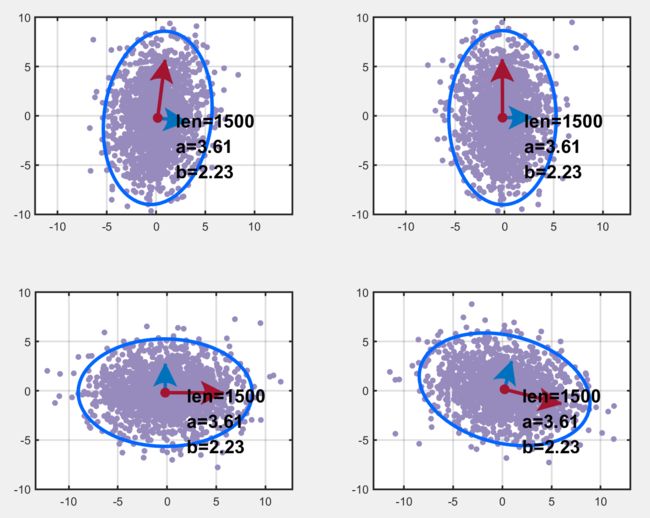
基于上述步骤，对于相关变量得到了其变换阵 $X1$，绘图结果如下，左上是原始数据，左下和右上对应中可行的转换矩阵，右下啥也不是。我们发现得到的变换阵 $X1$ 并不是 $Z^{-1}$ （$Dat{a}_Y=Dat{a}_X\cdot Z$），这说明变换阵不唯一？

代码如下：

%% PCA 求 变换矩阵 并绘图
function Test3()
len=300;
data=randn(5*len, 2);       % get the data 
data(:,1)=2*data(:,1);      % 第一列方差变为2
Z=[1 1;-1 3];
data1=data*Z;
A=data1'*data1/(5*len);
[X,D]=eig(A);               % 求特征值 D 和特征向量 X; X 各列是相应的特征向量
% A*X(:,1)-D(1,1)*X(:,1)
data2=data1*X;
X1=[X(:,2),X(:,1)];         % 因为第一个特征值比较大，所以优先将第一个特征向量放在前面
data3=data1*X1;
data4=data1*X1';            
% Plot
subplot(2,2,1);
PCA(data1);                 % 原始数据
subplot(2,2,2);
PCA(data2);                 % 去相关之后的 y 轴长
subplot(2,2,3);
PCA(data3);                 % 去相关之后的 x 轴长
subplot(2,2,4);
PCA(data4);                 % 啥也不是
end

PS：实际上，笔者使用的 PCA 函数中已经做了主成分分析（求出了样本的方差-协方差矩阵），里面用的是 Matlab 自带的 pca 函数，为了更详细地了解 PCA 的过程，笔者又做了点额外工作，PCA 函数在本博文中仅仅发挥一个画图的功能。

Reference

• 主成分分析 (PCA) 的主轴和置信椭圆可视化
• 主成分分析（PCA）原理详解
• PCA的数学原理
• 置信椭圆与R画法
• Matlab 让多图排版更美观
• 矩阵的各种分解汇总
• 注：上面的代码已经很全了，笔者也提供了测试时所使用的.m文件，戳我下载。