【1995-JG-Teunissen】最小二乘降相关平差：一种GPS整周模糊度快速估计方法（原文的部分翻译）

原文：Teunnissen P J G. The least-square ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation [J]. J. Geodesy, 1995, 70(1): 65-82.
LAMBDA 搜索模糊度固定方法是 Teunissen 大佬于1995 年提出的（原文戳我可下），本篇博文对其部分内容进行了翻译。笔者水平有限，不当之处还望不吝赐教。

Abstract

下面的内容当然不是原文的摘要啊，而是笔者的一些经验和教训，原文摘要没有翻译。

• 拒绝机翻，因为一旦有一种结果，无论其好坏，总会说服自己去接纳它。
• 写这篇文章的初衷是想仔细研究一下 LAMBDA 搜索，但是后来发现翻译实在是太慢了，所以就中途跳了一些，最后彻底放弃了。
• 翻译过程中，确实也学到了很多有用的词汇，但是这样做性价比真的不高！！
• 因为国内已经有很多高水平的相关博士论文，为什么还要自己再从原文一点一点地学呢？站在巨人的肩膀上俯瞰不更好吗？
• 但是也并不是一点用也没有，原文中 Teunissen 大佬做了详尽的分析（虽然这些分析看起来也是一知半解），这些在很多博士论文中是很难看到的，然后也挺锻炼自己的语言组织能力的。但是这种方法，在这个浮躁的社会中之会被认定会性价比低，不值得；但是如果真正吃透一篇经典的英文论文，所得的收益是无比巨大的，什么狗屁的性价比，都是浮云。
• 这篇博文就这样吧，没时间搞下去了，有问题不负责哈，仅供参考。

1. Introduction

在本文中，一种新的对于双差载波相位模糊度最小二乘估计方法将被提出。这种方法包括两步。在第一步，将原始双差模糊度通过一个模糊度变换 $Z^{\ast }$ 重新参数化，变成一个具有某些理想性质的新的模糊度。用 $a$ 表示原始模糊度向量，其实数最小二乘解记为 $\hat{a}$，并且其方差协方差矩阵为 $Q_{\hat{a}}$，那么经过变换后的新模糊度 $z$ 可表示如下：
$$z=Z^{\ast }a,\hat{z}=Z^{\ast }\hat{a},Q_{\hat{z}}=Z^{\ast }{Q}_{\hat{a}}Z\text{\hspace{1em}(1)}$$
模糊度变换矩阵 $Z^{\ast }$ 所有元素都是整数且其行列式绝对值为 1 [19]。当然，对双差模糊度做转换的想法并不是完全新的。GPS 观测值的某些线性组合已经在模糊度固定问题上发挥了突出的作用。尤其是“宽巷”技术已经被证明是非常成功的。比较有名的例子是窄巷、宽巷和超宽巷组合 [20-22]。除此之外，其他宽巷组合也被研究了 [23]。然而目前各种整数线性组合的研究只限于单通道双频的情况。因此这些方法需要双频载波相位数据。此外，这些方法只考虑了单通道的情况，没有顾及到接收机-卫星的几何形状（就是说它们只针对一颗星组宽巷超宽项，没有考虑到卫星间的联系）。而上面所述的模糊度变换矩阵 $Z^{\ast }$ 本身并不需要使用双频载波相位观测值，并且考虑到了接收机到卫星的几何构型缓慢变化，因为在模糊度的方差协方差矩阵 $Q_{\hat{a}}$ 中强调了这一点。

一旦得到了转换后的模糊度，第二步就会进行整数最小二乘模糊度搜索。因为进行了模糊度变换缩小了搜索空间，所以其搜索效率也得到了提高，搜索是基于 $\hat{z}$ 的序贯条件最小二乘平差进行的。对于条件最小二乘模糊度估计而言，变换后的模糊度搜索空间由下述不等式描述：
$$\sum _{i=1}^n({\hat{z}}_{i|I}-z_i{)}^2/{\sigma }_{\hat{z}(i|I)}\le {\chi }^2\text{\hspace{1em}(2)}$$
其中，${\hat{z}}_{i|I}$ 表示以前一个 (第 $i-1$ 个) 模糊度为条件的，第 $i$ 个模糊度的最小二乘估计，${\hat{z}}_{i|I}$ 表示其方差。${\chi }^2$ 是一个合适的正数，用以确保模糊度搜索空间确实包含所需求的整数最小二乘模糊度。正是上述不等式中的平方之和的结构，为各个模糊度形成了边界，从而能够对转换后的整数最小二乘模糊度 $\check{z}$ 进行搜索。尽管平方和结构本身并不新，但是在如何解释和使用它来进行搜索方面有着重要的区别[13], [16,17], [24]。一旦整数模糊度估值 $\check{z}$ 被确定后，相应的基线解 $\check{b}$ 可以被恢复为：
$$\check{b}=\hat{b}-Q_{\hat{b}\hat{z}}{Q}_{\hat{z}}^{-1}(\hat{z}-\check{z})\text{\hspace{1em}(3)}$$
其中 $\hat{b}$ 表示没有固定的最小二乘基线解。

这种方法最根本的问题就是模糊度变换矩阵 $Z^{\ast }$ 的构造和模糊度搜索的实现。因为一旦所有的模糊度都不相关了，那么整数最小二乘模糊度估计就变得极其容易。因为不相关的模糊度的置信椭圆体将于网格轴对齐，寻求整数最小二乘模糊度解将简单地从实数最小二乘估计值四舍五入得到。当条件最小二乘估计值与非条件估计值相同时，即当 ${\hat{a}}_{i|I}\equiv {\hat{a}}_i$ 对于所有的 $i$ 都成立时，模糊度将是完全不相关的。然而在 GNSS 领域，最小二乘模糊度是高度相关的，并且它们的置信椭圆是极其细长的。这在很短的观测时间段和缺乏高精度伪距观测值的情况下极其显著。由于模糊度方差-协方差矩阵的内在结构特点，模糊度条件方差的频谱 ${\sigma }_{\widehat{i|I}}(i=1,\cdots ,n)$ 在从第三个条件方差到第四个条件方差的过程中，通常显示出一个很大的不连续性。但这意味着，当上述不等式被用于原始参数化时，搜索将受到前三个模糊度的界限相当宽松的影响，而其余模糊度的界限则极其严格。因此这种方法的精髓在于构造一个可以消除模糊度条件方差的频谱不连续性的降相关模糊度变换矩阵 $Z^{\ast }$。在二维空间中，这是通过基于完全去相关条件最小二乘变换的整数近似来实现模糊度变换的。这种类型的变换也称为高斯变换，对于非整数情况，它们被认为是将矩阵中的条目归零的基本工具 [25]。在n维情况下，通过反复使用二维去相关模糊度变换来解决。但是，它不是采用于无条件的模糊度，而是采用有条件最小二乘模糊度对。基于文献[26]思想的这种方法受到GPS模糊度条件方差典型不连续性的影响。我们方法的成功很大程度上归因于这种不连续性的存在，并且它强调了卫星冗余和双频数据的相关性。一旦条件方差频谱被展平，返回的模糊度不再相关且非常精确，从而允许以高效的方式执行变换整数最小二乘模糊度的搜索。

为了正确判断本贡献的意义，重要的是，我们要区分以下两个GPS模糊性固定的问题：模糊度估计问题和模糊度验证问题。

本文只涉及第一个问题，而不是第二个问题。第二个问题取决于第一个问题的结果，它涉及到对估计的整数模糊度的验证。尽管目前在实践中使用的验证估计模糊度的程序似乎效果令人满意，但作者认为，这些验证程序的理论基础仍有一些改进的余地。为了对估计的模糊度以及相应的基线解决方案进行适当的统计评估，如果能够掌握相应的整数估计器的概率密度，确实会很有帮助。然而，这是一个非简单的问题，但可以参考[13]，[27-29]中的讨论。尽管适当的验证程序很重要，但本贡献只关注整数模糊度估计问题。因此，无妨强调一下，我们的方法虽然高效，但如果数据被未建模的影响所污染，仍可能得出错误的整数模糊度。

2. The GPS Ambiguity Estimation Problem

GPS 模糊度估计问题

2.1 The Carrier-Phase Observation Equation

载波相位观测方程

载波相位观测方程被表示如下：
$$\Phi =||r-R||+c(dt-dT)+\lambda N+ϵ\text{\hspace{1em}(4)}$$
上式中 $dt,dT$ 分别表示卫星和接收机钟差，$ϵ$ 表示载波相位观测值噪声和偏差比如卫星星历误差、对流层电离层延迟、多径造成的随机误差等。（其他符号都是常用的）在相位数据处理过程中，载波相位观测值在站星间做差分处理是很常见的。下面给出了载波相位双差观测方程：
$$DD\Phi =DD||r-R||+\lambda DDN+DDϵ\text{\hspace{1em}(5)}$$
其中DD代表双差分算子。在这个方程中，模糊项DDN是已知的整数值。为了简单起见，我们将在下文中假设只有两个接收机的情况下。然而，这对所提方法的普遍适用性没有影响。该方法与使用的接收机数量无关，因此也适用于使用两个以上接收机的情况。例如，当GPS数据在网络模式下被同时平差时，就是这种情况。

对未知参数的观测方程进行线性化，并将这些线性化方程集合成一个线性方程组，就可以得到：
$$y=Aa+Bb+e\text{\hspace{1em}(6)}$$
其中，$y$ 表示双差载波相位观测值的 $omc$；$a$ 是未知的整周双差模糊度向量；$b$ 是未知的基线部分的增量向量；$A,B$ 是 $a,b$ 的设计矩阵；$e$ 是未模型化的误差向量。

这个观测方程组被作为计算未知参数 $a$ 和 $b$ 的估值的出发点。我们的估计标准将基于最小二乘的原则。从统计学的角度来看，这一选择的动机是，在没有建模错误的情况下，适当加权的线性最小二乘估计值与无偏最小方差估计值相同。此外，如果相位观测量的正态性假设成立，这些估计器也是最大似然估计器。在下文中，我们将假设 $e$ 中的偏置项已被纠正或足够小，可以忽略不计。

2.2 Integer Least-Squares Estimation

整数最小二乘估计
为解决像公式(6)那种线性（或线性化）系统的最小二乘标准可以被写成如下形式：
$$\underset{a,b}{\min }||y-Aa-Bb|{|}_{Q_y}^{2}witha\in Z^n,b\in R^3\text{\hspace{1em}(7)}$$
其中，$||\cdot |{|}_{Q_y}^2=(\cdot )\ast Q_y^{-1}(\cdot )$，$Q_y$ 是双差载波相位观测值的方差-协方差矩阵；$Z^n$ 是 n 维的整数空间；$R^3$ 是三维的实数空间；使得公式(7)最小的 $a,b$ 分别记为 $\check{a}\in Z^n,\check{b}\in R^3$。注意到，式(7)是一个有限制条件的最小二乘问题。这是因为整数约束 $\check{a}\in Z^n$ 的存在，最小化式(7)的问题因此被称为整数最小二乘问题。

上述整数最小二乘法问题的二次目标函数可以分解为三个平方之和。
$$||y-Aa-Bb|{|}_{Q_y}^2=||\hat{e}|{|}_{Q_y}^2+||\hat{b}|a-b|{|}_{Q_{\hat{b}|a}}^2+||\hat{a}-a|{|}_{Q_{\hat{a}}}^2\text{\hspace{1em}(8)}$$
其中，$\hat{a}$ 是标准最小二乘估计而得的实数模糊度，其方差-协方差矩阵为 $Q_{\hat{a}}$；$\hat{b}|a$ 整数 $a$ 约束条件下的最小二乘基线向量，其方差-协方差矩阵为 $Q_{\hat{b}|a}$；$\hat{e}$ 是标准最小二乘估计的残差向量。从上面的分解可以看出，如果式(8)在 $a\in R^n,b\in R^3$ 的条件下最小化，那么其后面两项将会完全消失。因此，当取 $\hat{a}\in R^n,\hat{b}\in R^3$ 时，目标函数取得最小值，其残差向量记为 $\hat{e}$。然而在我们这种情况下，目标函数需要在 $a\in Z^n,b\in R^3$ 的条件下进行最小化。在这种情况下，只有第二项会消失。假设目标函数是在 $\check{a}\in Z^n,\check{b}=\hat{b}|\check{a}\in R^3$ 的条件下取得最小值，那么相应的最小化目标函数是 $||\hat{e}|{|}_{Q_y}^2+||\hat{a}-\check{a}|{|}_{Q_{\hat{a}}}^2$。

上面的讨论说明(7)式所说的整数最小二乘问题可以分为两步解决。第一步是用 $R^n$ 替换 $Z^n$ 求解最小化式(7)（也就是求解实数模糊度），因此在第一步中的整数约束就被移除了，将此问题变为了一个一般的最小二乘问题。基于第一步的结果，实数模糊度 $\hat{a}$ 和基线向量 $\hat{b}$ 就被估计得到了，并且它们相应的方差-协方差矩阵为：
$$\left(\begin{array}{c}\hat{a}\\ \hat{b}\end{array}\right),\left(\begin{array}{cc}{Q}_{\hat{a}}& Q_{\hat{a}\hat{b}}\\ Q_{\hat{b}\hat{a}}& Q_{\hat{b}}\end{array}\right)\text{\hspace{1em}(9)}$$
第一步的结果作为第二步的输入，在第二步通过整数最小二乘估计出模糊度向量 $\check{a}$，其目标函数为：
$$\underset{a}{\min }(\hat{a}-a)Q_{\hat{a}}^{-1}(\hat{a}-a)witha\in Z^n\text{\hspace{1em}(10)}$$
一旦整数模糊度向量 $\check{a}\in Z^n$ 被得到，残差 $(\hat{a}-\check{a})$ 被用来调整无约束的基线解 $\hat{b}$ 以此来得到整数 $\check{a}$ 约束下的基线解 $\check{b}=\hat{b}|\check{a}$：
$$\check{b}=\hat{b}|\check{a}=\hat{b}-Q_{\hat{b}\hat{a}}{Q}_{\hat{a}}^{-1}(\hat{a}-\check{a})\text{\hspace{1em}(11)}$$
上述逐步方法在概念上与实践中通常遵循的程序一致，当固定模糊度包含在基线计算中时也是如此。估计结果 $\hat{a},\hat{b}$ 有时被称为浮点解，由式(7)得出的估计结果 $\check{a},\check{b}$ 被称为固定解。

值得注意的是，式(10)所示的最小化问题可能得到的解不唯一。虽然很不可能有多于一个解，但原则上，公式(10)最多可能有 $2^n$ 个不同的整数最小值解。即便如此，在接下来的讨论中，我们仍然假设公式(10)有且仅有一个解。我们这样做的动机是，当公式(10)的解不唯一时，用此来固定模糊度也认为是不可行的。

$\hat{b}|\check{a}$ 的方差协方差矩阵为 $Q_{\hat{b}|a}=Q_{\hat{b}}-Q_{\hat{b}\hat{a}}{Q}_{\hat{a}}^{-1}{Q}_{\hat{a}\hat{b}}$。在实践中，方差-协方差矩阵通常被用来描述最后基线解 $\check{b}$ 的精度（然而，这些方法在缩放该矩阵的方式上可能存在差异）。然而在这里，一些谨慎的定论是有必要的 [27]。式(11)的结构显示 $\check{b}$ 可以被理解为最小二乘估计。从式(9)的结果出发，$\check{b}$ 可以被理解为整数模糊度向量 $\check{a}$ 约束下的 $b$ 的最小二乘估计。而和这种解释相一致的是，$\check{b}$ 的精度确实被描述为方差-协方差矩阵 $Q_{\hat{b}|a}$，当这样做的时候，我们必须意识到 $Q_{\hat{b}|a}$ 是一个条件方差-协方差矩阵。因此，在预测未来实验的实际结果方面，应该给予形式方差-协方差矩阵 $Q_{\hat{b}|a}$ 以下含义。当在相似的情况下重复足够多次数的测量实验时，当所有基线解都基于相同的 $a$ 值时，矩阵 $Q_{\hat{b}|a}$ 描述了各基线解中可以期望的传播（spread）。但这表明，由于在实践中，每个基线解算对于模糊度向量 $a\in Z^n$ 都有它自己的整数估计，严格来说， $Q_{\hat{b}|a}$ 并没有描述它应该描述的东西。换句话说， $Q_{\hat{b}|a}$ 是 $\hat{b}|a$ 的方差-协方差矩阵，但是并不一定是 $\check{b}=\hat{b}|\check{a}$ 的方差-协方差矩阵。模糊度向量的最小二乘估计值是整数，这并不意味着它是非随机的。我们需要的实际上是 $\check{b}$ 的无条件方差-协方差矩阵。因此，为了获得 $\check{b}$ 的理论上正确的方差-协方差矩阵，在对式(11)运用误差传播定律时，应考虑整数模糊度向量的随机性。这是一个不简单的问题（$\check{a}$ 的概率密度函数是离散型的），而且从理论上看，这个问题还没有得到满意的解决。幸运的是，这个问题的实际意义可能不大，特别是当一个合理的验证程序被用于验证 $\check{a}$ 的时候。一个适当的验证程序的特点之一应该是验证是否有足够的概率可能性（probability mass）位于 $Z^n$ 的一个格点上。而当这一点能够得到足够程度的保证时，$\check{a}$ 的随机性对 $\check{b}$ 的影响就会很小，矩阵 $Q_{\hat{b}|a}$ 可以被当作 $\check{b}$ 精度的一个现实可行的测量。

我们清楚地知道 $Q_{\hat{b}|a}<Q_{\hat{b}}$。当使用的是短时间观测，我们实际上有 $Q_{\hat{b}|a}<<Q_{\hat{b}}$。下面将解释原因。因为 GPS 卫星的轨道高度很高，卫星和接收机间的相对位置变化的很慢，这意味着在短时观测情况下，实数模糊度和基线坐标很难分离开来，这将导致被估计的基线精度很差。然而当人们明确地以固定整数模糊度为目标并假定它们的离散概率密度函数具有足够高的峰值时，载波观测值便可以当作高精度的伪距观测值。这时，基线解将会有足够高的精度，并且其方差阵 $Q_{\check{b}}\cong Q_{\hat{b}|a}<<Q_{\hat{b}}$. 因此，模糊度固定的唯一目的是：通过加入整数约束 $a\in Z^n$，使得基线解的精度大大提高。当模糊度被视为实数时，需要漫长的观测时间才可以得到高精度的基线解，所以模糊度固定可以避免漫长的观测时间。

在接下来的部分，我们并不是将注意力直接放在基线解上面，而是将注意力放在求解整数模糊度问题（式(10)）上面。正式由于受限于目标函数最小化的条件，整数模糊度估计问题才变得如此复杂。

2.3 Sequential Conditional Least-Squares Estimation

序贯条件最小二乘估计
不幸的是，由于整数约束 $a\in Z^n$ 的存在，没有标准的技术可以用来解决式(10)，但是有解决普通最小二乘问题的方法。因此我们不得不求助于某种方式利用离散搜索策略来寻找式(10)的整数最小值的方法。然而，在我们开始考虑建立这种搜索策略之前，我们如果考虑了这样一个问题『为了能够应用最简单的整数估计方法，式(10)的结构需要是什么？』，这将会有所帮助。显然，最简单的整数估计方法是『四舍五入』，当应用于式(10)时，只需要模糊度方差阵 $Q_{\hat{a}}$ 是对角阵，也就是说，当所有的最小二乘模糊度完全不相关时，这种方法才可以得到正确的解算结果。对角阵 $Q_{\hat{a}}$ 意味着式(10)将被简化为下面的独立方差平方和的形式：
$$\underset{a_1,\cdots ,a_n\in Z^n}{\min }\sum _{i=1}^n({\hat{a}}_i-a_i{)}^2/{\sigma }_{\hat{a}(i,i)}$$
其中，${\sigma }_{\hat{a}(i,i)}$ 表示第 $i$ 个最小二乘模糊度的方差。因此，在这种情况下，问题就变成了 $n$ 个独立的整数最小二乘问题。而这些独立的整数最小二乘问题就可以用『四舍五入』来解决。因此，当所有的最小二乘模糊度是完全不相关时，模糊度最小二乘问题就变得微不足道了。

不幸的是，最小二乘模糊度是高度相关的，其方差-协方差矩阵 $Q_{\hat{a}}$ 和对角阵相差很远。如果我们将 $Q_{\hat{a}}$ 对角化，那么将目标函数转化成平方和的形式依然是有可能的。然而并不是所有的对角化都有效，需要的是像式(12)那样的，将各个模糊度分配到总和中的各个平方项中。这就排除了基于模糊度方差矩阵的特征分解的对角化。本着和分解(8)式相同的精神，我们对模糊度进行条件最小二乘分解。而这将在逐个模糊度的基础上进行。因此，一个序贯条件最小二乘估计方法将被应用。这意味着第一个最小二乘模糊度 ${\hat{a}}_1$ 保持不变，而第二个最小二乘模糊度将会被它在第一个模糊度 $a_1$ 条件下进行的最小二乘结果所替代，也就是说，${\hat{a}}_{2|1}={\hat{a}}_2-{\sigma }_{{\hat{a}}_{(2,1)}}{\sigma }_{{\hat{a}}_{(1,1)}}^{-1}({\hat{a}}_1-a_1)$，值得注意的是 ${\hat{a}}_{2|1}$ 和 $a_1$ 不相关。第三个最小二乘模糊度将会被它在第一个和第二最小模糊度 $a_1,a_2$ 的条件下进行的最小二乘结果替代，即 ${\hat{a}}_{3|2,1}={\hat{a}}_3-{\sigma }_{{\hat{a}}_{(3,1)}}{\sigma }_{{\hat{a}}_{(1,1)}}^{-1}({\hat{a}}_1-a_1)-{\sigma }_{{\hat{a}}_{(3,2|1)}}{\sigma }_{{\hat{a}}_{(2|1,2|1)}}({\hat{a}}_{(2|1)}-a_2)$，同样的，${\hat{a}}_{3|2,1}$ 和 ${\hat{a}}_{2|1},a_1$ 不相关。递推下去，我们将 ${\hat{a}}_{j|(j-1),\cdots ,1}$ 简记为 ${\hat{a}}_{j|J}$，进行到第 $i$ 步时：

$${\hat{a}}_{i|I}={\hat{a}}_i-\sum _{j=1}^{i-1}{\sigma }_{{\hat{a}}_{(i,j|J)}}{\sigma }_{{\hat{a}}_{(j|J,j|J)}}^{-1}({\hat{a}}_{(j|J)}-a_j)\text{\hspace{1em}(13)}$$

并且 ${\hat{a}}_{i|I}$ 和 ${\hat{a}}_{j|J},(j=1,\cdots ,i-1)$ 不相关。根据式(13)，模糊度之差 $({\hat{a}}_i-a_i)$ 可以被写作：$({\hat{a}}_i-a_i)=({\hat{a}}_{i|I}-a_i)+\sum _{j=1}^{i-1}{\sigma }_{{\hat{a}}_{(i,j|J)}}{\sigma }_{{\hat{a}}_{(j|J,j|J)}}^{-1}({\hat{a}}_{(j|J)}-a_j)$ . 记 $\hat{d}=({\hat{a}}_1,{\hat{a}}_{2|1},\cdots ,{\hat{a}}_{n|N}{)}^{\ast }$。因此，应用误差传播律，并且条件最小二乘模糊度是互相不相关的，将上式写成向量-矩阵的形式如下：
$$(\hat{a}-a)=L(\hat{d}-a),Q_{\hat{a}}=LD{L}^{\ast }\text{\hspace{1em}(14)}$$
其中，$D=diag.(\cdots ,{\sigma }_{(i|I,i|I)},\cdots )$ 是对角阵，并且 $(L{)}_{ij}=0(1\le i<j\le n)$ ， $(L{)}_{ij}=1(i=j)$ 和 $(L{)}_{ij}={\sigma }_{{\hat{a}}_{(i,j|J)}}{\sigma }_{{\hat{a}}_{(j|J,j|J)}}^{-1}(1\le i<j\le n)$ 上述的矩阵分解就是有名的 $LD{L}^{\ast }$-分解[25]。对 $LD{L}^{\ast }$-分解的“重新发现”，我们可以对下三角矩阵 $L$ 和对角阵 $D$ 中的每一项给出一个明确的统计解释。这种解释对于下一章中模糊度转换的构造也有帮助。将式(14)代入(10)的目标函数，可以得到所需的平方和结构，并允许我们将整数最小二乘问题重写为：
$$\underset{a_1,\cdots ,a_n\in Z^n}{\min }\sum _{i=1}^n({\hat{a}}_{i|I}-a_i{)}^2/{\sigma }_{\hat{a}(i|I,i|I)}\text{\hspace{1em}(15)}$$
值得注意的是，当所有的最小二乘模糊度都不相关时，式(15)所示的平方和减少到式(12)所示的平方和形式。还要注意的是，在式(15)所示的情况下，简单的“四舍五入”并不一定能得到式(10)所示的正确的整数最小值。这是由于 ${\hat{a}}_{i|I}$ 取决于 $a_j(j=1,2,\cdots ,i-1)$. 但是式(15)所示的平方之和结构仍然允许我们为单个模糊度设置尖锐（sharp）的界限，这将在下一节展示。

2.4 Search for the Integer Least-Squares Ambiguities

整数最小二乘模糊度搜索
为了解决式(15)所示的问题，我们首先限制解空间，用一个可以列举的较小的子集代替整数空间 $Z^n$。这个想法是利用式(15)的目标函数在 $R^n$ 中引入一个椭圆区域，在此基础上进行搜索，这个椭圆性的模糊度搜索空间是由以下因素确定的：
$$\sum _{i=1}^n({\hat{a}}_{i|I}-a_i{)}^2/{\sigma }_{\hat{a}(i|I,i|I)}\le {\chi }^2\text{\hspace{1em}(16)}$$
这个椭圆区域是以 $\hat{a}\in R^n$ 为中心的，它的方向和扁率由模糊度方差-协方差矩阵 $Q_{\hat{a}}$ 所控制，它的大小可以通过选择正常数 ${\chi }^2$ 来控制。我们假设正常数 ${\chi }^2$ 的选择使该区域至少包含所寻求的使式(15)取得最小值的整数解[24]。

为了讨论我们的整数最小二乘模糊度搜索，我们首先考虑两维的情况。对于 $n=2$，不等式16变为
$$({\hat{a}}_1-a_1{)}^2/{\sigma }_{\hat{a}(1,1)}+({\hat{a}}_{2|1}-a_1{)}^2/{\sigma }_{\hat{a}(1,1)}\le {\chi }^2\text{\hspace{1em}(17)}$$
椭圆形的区域如图一所示。图中显示了一个包裹椭圆区域的长方形和一条直线，直线经过了椭圆的中心 $({\hat{a}}_1,{\hat{a}}_2)$，其方向向量是 $(1,{\sigma }_{{\hat{a}}_{(2,1)}}{\sigma }_{\hat{a}(1,1)}^{-1})$。直线交椭圆于两点，在这两点上，椭圆的法线沿着 $a_1$ 轴。值得注意的是，当 $a_1$ 变化时，点 $(a_1,{\hat{a}}_{2|1})$ 沿着这条线移动。根据式(17)，我们模糊度 $a_1,a_2$ 下面两个边界：
$$\{\begin{array}{c}\begin{array}{rl}& ({\hat{a}}_1-a_1{)}^2\le {\sigma }_{a(1,1)}{\chi }^2\\ & ({\hat{a}}_{2|1}-a_2{)}^2\le {\sigma }_{{\hat{a}}_{(2|1,2|1)}}\lambda (a_1){\chi }^2\end{array}\end{array}\text{\hspace{1em}(18)}$$
其中 $\lambda (a_1)=1-({\hat{a}}_1-a_1{)}^2/{\chi }^2{\sigma }_{a(1,1)}$. 相应的间隔及长度如图一所示。

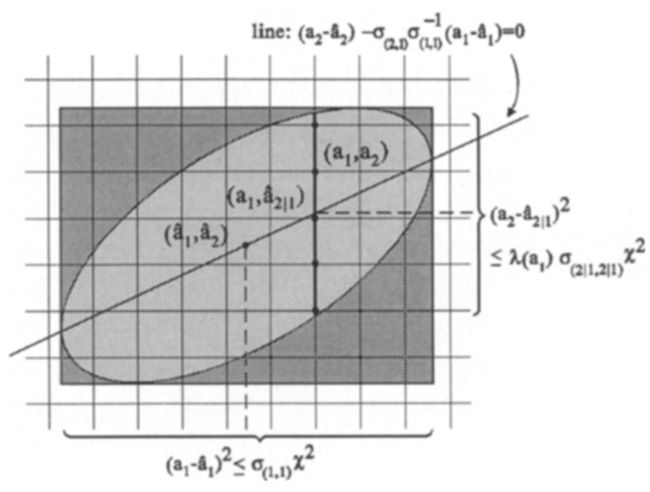
我们对整数最小二乘模糊度的搜索过程如下所示。首先，首先选择一个整数模糊度 $a_1$ 满足式(18)的第一个条件，假设这两个模糊度是排好序的，第一个是精度最高的最小二乘模糊度，即 ${\sigma }_{\hat{a}(1,1)}\le {\sigma }_{\hat{a}(2,2)}$，接着，基于上面选择的整数模糊度的值 $a_1$，计算条件最小二乘估计值 ${\hat{a}}_{2|1}$ 和标量 $\lambda (a_1)$。这些数据被用来选择满足式(18)第二个边界条件的整数模糊度 $a_2$。我们的目标是选择整数极小值，因此选择整数候选者的方式是使平方和式(17)中的各个平方项尽可能的小。者意味着 $a_2$ 应该总是取到最近的整数 ${\hat{a}}_{2|1}$。但是，注意到 ${\hat{a}}_{2|1}$ 取决于 $a_1$。对于第一个被选择为最接近的整数 ${\hat{a}}_1$ 的 $a_1$，如果不能找打一个满足第二个边界条件的 $a_2$，那么应该重新选择 $a_1$ 和其最接近的整数 ${\hat{a}}_1$. 值得注意的是，在这种方式中，大致沿着直线 $(a_1,{\hat{a}}_{2|1})$ 的方向，在椭圆的内部以交替的形式，沿着 $a_1$ 轴向椭圆的边界移动。

2.5 The GPS Spectrum of Ambiguity Conditional Variances

3. The Reparametrized Ambiguity Estimation Problem

3.1 The Class of Admissible Ambiguity Transformations

3.2 A 2D-Decorrelating Ambiguity Transformation

3.3 Flattening the Spectrum of Ambiguity Conditional Variances

3.4 On the Spectrum and the Gain in Baseline Precision

4. Summary and Concluding Remarks

5. References

略略略，可看原文